Эськов В.Д., Каталевская А.В. Теоретические основы электротехники. Часть 2

Подождите немного. Документ загружается.

181

ляющих вектора магнитной индукции используем формулу (13.59а), а

чтобы найти векторный магнитный потенциал, результат проинтегриру-

ем:

333

Bdr C 



Постоянную интегрирования

найдем из усло-

вия непрерывности вектора

А на внутренней поверхности оболочки ка-

беля

().rr

Опуская промежуточные выкладки, запишем результат:

)(2

)(

lnln

)(2

)(































rrr

rrI

(13.63)

Что касается четвертой области, то в ней магнитное поле отсут-

ствует, поскольку одинаковые по величине токи в центральном и

наружном проводниках протекают в противоположных направлениях.

Этот вывод следует из закона полного тока. Поэтому

0,B 

а вектор-

ный магнитный потенциал постоянен:



13.4.4. Расчет индуктивностей

В этом разделе рассматриваются статические индуктивности, кото-

рые зависят от геометрии системы проводящих контуров с токами, маг-

нитной проницаемости среды и самих проводников. Если

const,





то

индуктивности не зависят от токов.

Получим общее выражение для взаимной индуктивности двух про-

водящих контуров произвольной формы, размеры поперечного сечения

которых малы как по сравнению с их длинами

и ,ll

так и с рассто-

янием между контурами (рис. 13.22, а).

Векторный магнитный потенциал в некоторой точке от первого

контура с током

подсчитаем по формуле (13.54):











где





магнитная проницаемость среды; R – расстояние от элемента тока

до рассматриваемой точки. Магнитный поток, создаваемый этим

током и пронизывающий второй контур, можно подсчитать по форму-

ле (13.53):

21 1 2

d





По определению (см. раздел [5.1]) взаимная

индуктивность второго контура по отношению к первому равна

182

21 21 1 2













. (13.64)

Здесь R – расстояние между элементами контуров

и .ddll

Легко убедиться, что вычисление взаимной индуктивности первого кон-

тура по отношению ко второму, в котором протекает ток

даст тот же

самый результат. Так что

12 21



как это и должно быть в со-

ответствии с принципом взаимности.

Вычислить подобным же образом собственную индуктивность без

каких-либо оговорок нельзя, поскольку двойное интегрирование по од-

ной и той же длине даст результат, не имеющий физического смысла.

Обычно потокосцепление контура с током и магнитного потока, им со-

здаваемого, представляют

в виде двух составляющих:

внш внт









Внешнее потокосцепление

внш



определяется магнитным потоком,

замыкающимся вне проводника (на рис. 13.22, а этот поток пронизывает за-

штрихованную площадку, ограниченную контуром

),l

а внутреннее

внт





в теле самого проводника, заключенного между внутренним конту-

ром

и внешним

. Если предположить, что ток сосредоточен на оси про-

водника, то первое слагаемое можно определить по формуле (13.64), учиты-

вая весь ток по длине

и весь магнитный поток за пределами контура

внш внш











Полагая далее, что радиусы закругления отдельных участков про-

водника значительно превышают размеры его поперечного сечения,

подсчитаем внутреннее потокосцепление, используя результаты расчета

магнитного поля внутри прямолинейного проводника с током, получен-

ные в примере 13.14.

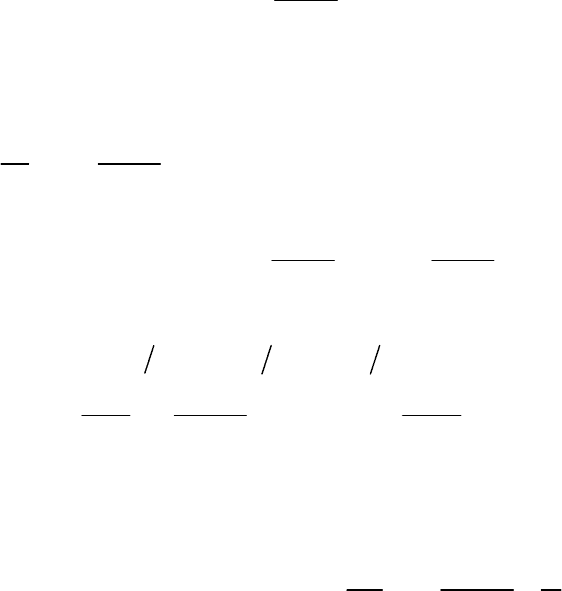
183

Магнитный поток, пронизывающий элементарную площадку ши-

риной dr и длиной

которая перпендикулярна плоскости чертежа на

рис. 13.22, б, равен

dBds ldr





 

Этот поток сцепляется с током

(/ ),

IrIrr





составляющим долю

// rrII



от всего тока I.

Значит, потокосцепление элементарного потока и тока составит

внт 1

ddlrdr









Тогда внутреннее потокосцепление

внт 1

lr dr











Теперь можно подсчитать и индуктивность:

внш внт внш внт

.LI I IL L









(13.65)

211

внш внт 2

Здесь , а , где











абсолют-

ная магнитная проницаемость окружающей проводник среды, а





проницаемость материала проводника. Если они равны (например, мед-

ный проводник в воздухе), то

12 1

dd l



















У достаточно

длинных и тонких проводников доля, вносимая внутренней индуктив-

ностью, несущественна. Если же провод изготовлен из ферромагнитно-

го материала, то эту добавку необходимо учитывать.

Пример 13.16. Индуктивность двухпроводной линии

Известны: d – расстояние между осями медных

()





проводов

воздушной линии,

r 

их радиусы.

Определить индуктивность единицы длины линии

Решение

Искомую величину определим по формуле (13.65), причем для вы-

числения внешней индуктивности воспользуемся результатами, полу-

ченными в примере 13.15. Магнитный поток, пронизывающий прямо-

угольную площадку между проводами линии длиной l и шири-

ной

2,dr

легко определяется по формуле (13.53). Действительно,

выполняя интегрирование по внутреннему контуру линии, следует

иметь в виду, что величина векторного магнитного потенциала в точках

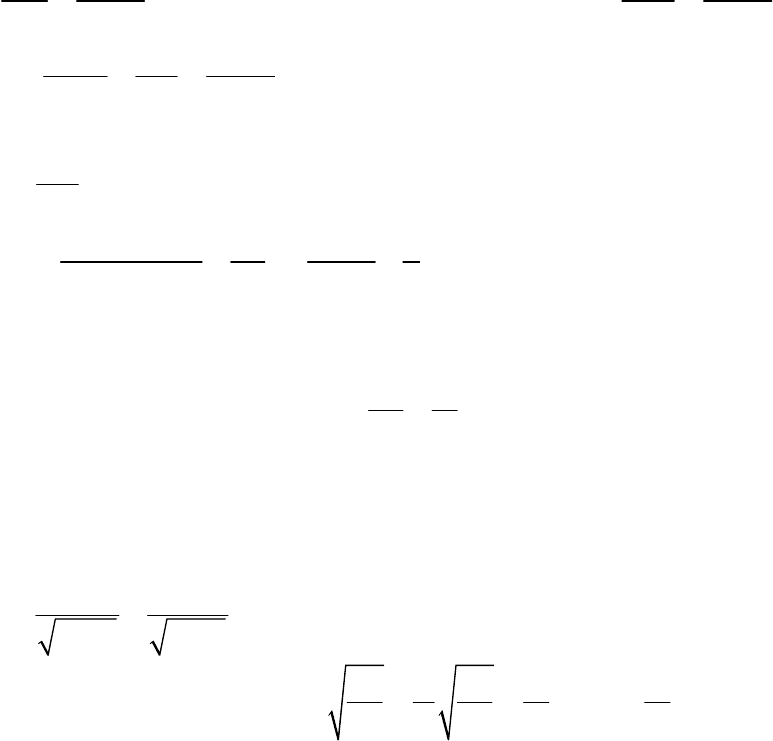
184

этого контура одинакова, а направление совпадает с направлением тока

соответствующего провода. Поэтому значения интеграла на сторонах

прямоугольника длиной l одинаковы:

dAdlAl





а на сторонах,

им перпендикулярных, обращаются в нуль.

Подставив в выражение (13.61)

10 2 0

иrr r dr





, находим

ln .









Затем вычисляем

внш

2ln

lI d r









внш

ln .

ldr









В свою очередь внутренняя индуктивность

двух проводов общей длиной 2l, как было показано выше, равна

внт





 Остается их просуммировать, приняв l равной единице дли-

ны:

внш внт

ln .

















В линиях электропередачи

,dr

поэтому, пренебрегая в этом

случае и внутренней индуктивностью, можно записать:

ln .







Сравним полученное выражение с формулой емкости единицы

длины линии (13.36). Налицо определенное сходство, диктуемое прин-

ципом двойственности, который проявлялся и в аналогии картин маг-

нитного и электростатического полей двухпроводной линии. Поэтому

дробь

00 00





равна скорости света, а волновое сопротив-

ление такой линии равно:

000 0

ln 120 ln .

Crr





 

Пример 13.17. Индуктивность коаксиального кабеля

Известны геометрические размеры кабеля (рис. 13.18) с медной

жилой и оболочкой из ферромагнитного материала с абсолютной маг-

нитной проницаемостью



Определить индуктивность единицы длины кабеля

Решение

Индуктивность кабеля длиной l можно представить в виде трех

слагаемых. Первое – это внутренняя индуктивность центрального про-

185

водника, которая определяется, как в примере 13.16, для одного провода

внт









Второе – внешняя индуктивность, которая связана с магнитным по-

током, замыкающимся внутри изоляции. На рис. 13.21 он пронизывает

прямоугольную площадку, перпендикулярную плоскости чертежа, дли-

ной l и шириной

.rr

При вычислении магнитного потока с помощью

формулы (13.53) обнаружим, что свой вклад в нее вносит лишь значе-

ние векторного магнитного потенциала на стороне прямоугольника,

совпадающей с внутренней поверхностью трубчатого проводника.

На внешней поверхности центрального проводника



в силу приня-

того при определении векторного магнитного потенциала условия. На

двух поперечных сторонах значение интеграла равно нулю, поскольку

векторы

и dAl

взаимно перпендикулярны. Поэтому искомый поток

внш

Al () ln , тогда ln .

lI l

dlA L

rIr











     



Третье слагаемое – это внутренняя индуктивность трубчатого про-

водника, которая определяется из расчета потокосцепления подобно то-

му, как это было сделано в начале раздела для

внт



применительно к

центральному проводнику. При этом следует использовать формулу

векторного потенциала

из (13.60а). Опуская вычисления, приведем

конечный результат:

)(2

внт





















Полное значение индуктивности на единицу длины кабеля равно

0 внт внш внт

()/.

LL Ll



 



Если не учитывать внутренние индуктивности проводников, то в

формуле останется одно слагаемое:

ln .







Характерно, что и это выражение обладает сходством с формулой

емкости единицы длины кабеля, полученной в примере 13.10. Сходство

обусловлено принципом двойственности, который упоминался при ана-

лизе результатов предыдущего примера. В кабеле, как и в двухпровод-

ной линии, скорость распространения электромагнитной волны не зави-

сит от его геометрических размеров, но оказывается меньше

скорости

света:

00 0







Ведь относительная диэлектрическая

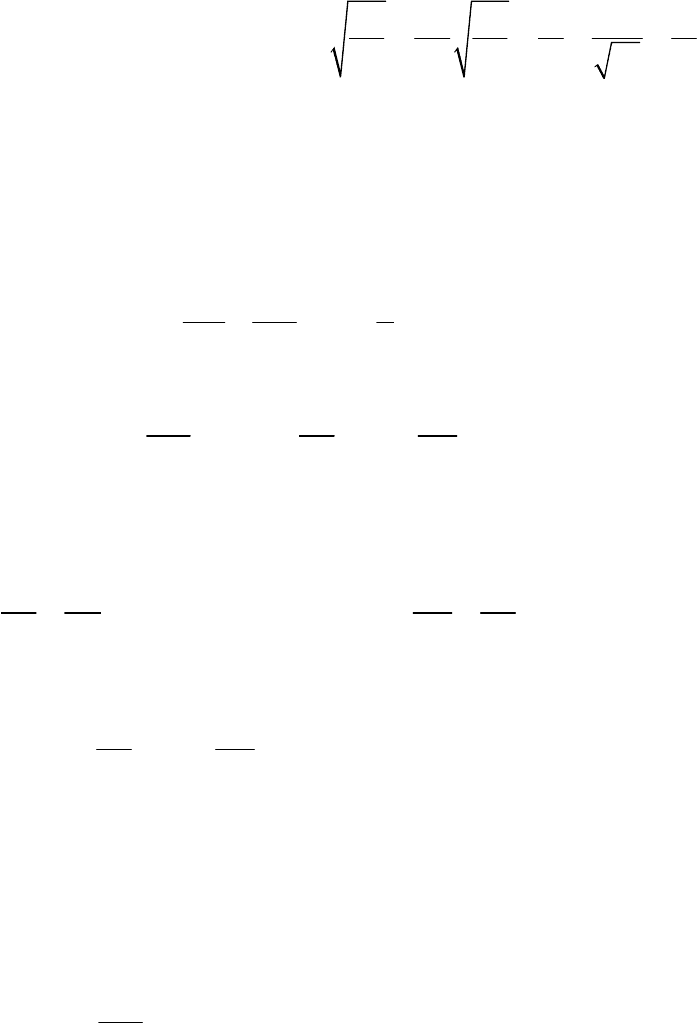
186

проницаемость изоляции





Эта же величина входит и в формулу

волнового сопротивления кабеля:

000

160

ln ln .

Crr







 

13.4.5. Теорема Умова–Пойнтинга

Как уже отмечалось в начале раздела 13.1, электромагнитное поле

является носителем определенного количества энергии и с его помощью

может осуществляться передача энергии на расстояние. Запас энергии в

некотором объеме V можно подсчитать с учетом соотношения (13.8):

ЭМ

().

22 2

VV V

W w dV dV dV











 

DE BH

Этот запас непрерывно изменяется во времени со скоростью

ttt

















Если изменение происходит за счет токов проводимости и смеще-

ния, плотность которых без учета тока переноса определяется по (13.5),

то из уравнений Максвелла (13.10) следует:

[] , [].

tt tt



  

 

 

ED HB

д EHE E

Таким образом, подынтегральное выражение в предыдущей формуле

можно представить в виде:

[][] .

 







EHEHHEE

Первые два слагаемых правой части с обратным знаком являются не

чем иным, как результатом вычисления дивергенции векторного произ-

ведения

[]EH

. Действительно, обращаясь с оператором «набла» как с

вектором, но не забывая, что он одновременно и символ дифференциро-

вания, можно записать:

[] [ ] [] [][ ].EH EH HE HE EH

Поэтому выражение скорости изменения энергии в объеме V мож-

но записать в виде:

[].

dV dV





  





EEH

Первый интеграл в правой части выражения учитывает потери

энергии в рассматриваемом объеме. Второй интеграл преобразуем по

теореме Остроградского–Гаусса:

[] [].

dV d







EH EH s



Он представля-

ет собой поток энергии, уходящей в единицу времени через замкнутую

поверхность S, ограничивающую объем V. Плотность этого потока (ко-

187

личество энергии, проходящей в единицу времени через единичную

площадку, нормальную к направлению потока энергии) выражается

вектором Пойнтинга

[].П EH

Теперь формула скорости изменения энергии может быть приведе-

на к виду, который представляет собой математическую запись теоре-

мы Умова–Пойнтинга:

dV d





 





E П s



(13.66)

Фактически эта теорема формулирует баланс мощностей для опре-

деленной области пространства. Поток вектора Пойнтинга, входящий в

замкнутую поверхность S, равен сумме двух слагаемых: мощности

тепловых потерь в объеме V, ограниченном этой поверхностью, и

мощности, с которой изменяются запасы энергии в том же объеме.

Пример 13.18. Передача энергии по коаксиальному кабелю

Известны напряжение между медной жилой и оболочкой кабеля U,

ток в этих проводниках I, а также их радиусы

012

,, ,rrr

обозначенные

на рис. 13.23, и абсолютная диэлектрическая проницаемость

изоляции



Оценить вектор Пойнтинга в различных частях кабеля.

Решение

Пусть центральный проводник имеет положительный заряд, а

наружный – отрицательный. Тогда вектор напряженности электриче-

ского поля

Е в изоляции практически лежит в плоскости, нормальной к

оси кабеля. Продольная составляющая этого вектора для силового кабе-

ля на несколько порядков меньше нормальной, и ею в первом прибли-

жении можно пренебречь. В проводниках вектор

Е совпадает по

направлению с током I, т. е. в центральном проводнике он направлен «к

нам», а в наружном – «от нас».

Вектор напряженности магнитного поля

Н имеет лишь азимуталь-

ную составляющую и в любой точке внутри кабеля направлен против

часовой стрелки.

Вектор Пойнтинга

П = [EH] в соответствии с правилом правоходо-

вого винта («буравчика») в изоляции направлен вдоль оси кабеля в ту

же сторону, что и ток в центральном проводнике, то есть от источника к

приемнику.

Все упомянутые выше векторы в различных точках кабеля (без со-

блюдения масштабов) также показаны на рис. 13.23. Каждая пара векто-

ров образует

прямой угол.

188

Количество энергии, проходящей в единицу времени через кольце-

образный элемент сечения радиусом r и толщиной dr, равно

2,dP EH r dr





где Е и Н определяются соответственно по форму-

лам (13.30а) и (13.59б):

10 0

ln( / ) 2

UBI

rrr r







Тогда

)/ln(

rrr

UIdr

dP 

и после интегрирования последнего выражения в преде-

лах от

доrr

найдем энергию, передаваемую сквозь сечение изоля-

ционного слоя в единицу времени:



Это не что иное, как мощ-

ность передачи энергии по кабелю. Так что передача энергии происхо-

дит не внутри проводников, а по разделяющему их изоляционному

слою. Проводники лишь обеспечивают ее движение в нужном направ-

лении.

При этом часть энергии поступает внутрь проводников для ком-

пенсации потерь на их нагревание. Например,

на поверхности цен-

трального проводника







 

поэтому внутрь про-

водника длиной l проникает в единицу времени энергия, покрывающая

джоулевы потери

22 2

001

2/(),

ПSl EH r l I l r I R



  

где

/( )Rl r







сопротивление жилы кабеля. Подобным же образом

можно показать, что энергия, проникающая в наружный проводник,

расходуется именно на его нагревание.

СПИСОК ЛИТЕРАТУРЫ

189

1. Демирчян К.С. Теоретические основы электротехники: в 3-х т. –

Т. 2 / К.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин, В.Л. Чечурин. –

СПб.: Питер, 2003. – 576 с.

2. Демирчян К.С. Теоретические основы электротехники: в 3-х т. –

Т. 3 / К.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин, В.Л. Чечурин. –

СПб.: Питер, 2003. – 377 с

3. Зевеке Г.В. Основы теории цепей / Г.В. Зевеке, П.А. Ионкин,

А.В. Нетушил, А.В. Страхов. – М.: Энергоатомиздат, 1989. – 528 с.

4. Бессонов Л.А. Теоретические основы электротехники. Электриче-

ские цепи / Л.А. Бессонов. – М.: Гардарики, 2007. – 701 с.

5. Бессонов Л.А. Теоретические основы электротехники. Электромаг-

нитное поле / Л.А. Бессонов. – М

.: Высшая школа, 1986. – 263 с.

6. Эськов В.Д. Курс лекций по теоретическим основам электротехни-

ки. Лекции 1–12 / В.Д. Эськов, А.В. Каталевская, А.Г. Сипайлов. –

Томск: Изд-во ТПУ, 2004. – 88 с.

7. Эськов В.Д. Курс лекций по теоретическим основам электротехни-

ки. Лекции 13–22 / В.Д. Эськов, А.В. Каталевская, А.Г. Сипайлов. –

Томск:

Изд-во ТПУ, 2006. – 100 с.

8. Эськов В.Д. Курс лекций по теоретическим основам электротехни-

ки. Лекции 23–34 / В.Д. Эськов, А.В. Каталевская, А.Г. Сипайлов. –

Томск: Изд-во ТПУ, 2007. – 100 с.

9. Эськов В.Д. Курс лекций по теоретическим основам электротехни-

ки. Лекции 35–44 / В.Д. Эськов, А.В. Каталевская. – Томск: Изд-во

ТПУ

, 2008. – 80 с.

190

ПРИЛОЖЕНИЕ 1

Оригиналы и изображения по Лапласу

№ Изображение Оригинал

1 p

1 δ(t)



a





a







pa

sin( )t





pp a

cos( )t







mp k















mp np k

pp p s





11 2 2

12 21

tpt

kmpnkp mpnkp

pp p p









, если корни знаменателя различные,



cos( )

Ae t









где

ks

()

()j

Ae m









если корни комплексно-сопряженные



  



  













() ()

me m n te







      







если корни равные,





ks

mp n







mp n p

pps







Частный случай формул (9),

где





