Эськов В.Д., Каталевская А.В. Теоретические основы электротехники. Часть 2

Подождите немного. Документ загружается.

171

Уравнения магнитного поля постоянных токов в дифференциаль-

ной форме выведены в разделе 13.1 (13.1б, 13.4б, 13.7):

rot , div 0, .



H д BBH

Первое из этих уравнений говорит о том, что в областях, занятых

током, магнитное поле имеет вихревой характер. А вне этих областей,

где

rot 0,H

магнитное поле безвихревое и, значит, потенциальное.

Иными словами, вектор напряженности магнитного поля можно пред-

ставить в виде

мм

grad .



 H

(13.48)

Тогда

div =0,



    BB H

откуда следует уравнение

Лапласа для скалярного магнитного потенциала



=0.





(13.49)

Для областей, занятых током, это уравнение не годится. Там можно

ввести новую функцию – векторный магнитный потенциал

А, который

связан с вектором магнитной индукции соотношением

rot .



BA A

(13.50)

В этом случае тождественно удовлетворяется принцип непрерыв-

ности магнитного потока:

div rot 0.



Тогда

rot 1

rot rot rot (grad div ) .

aaa





 

HAAд

Если, не нарушая соотношения (13.50), в последнем выражении

принять

div 0,A

то из него следует уравнение Пуассона для векторно-

го магнитного потенциала

А:



A

(13.51а)

Естественно, в областях, незанятых током

(0),



оно переходит в

уравнение Лапласа



A

(13.51б)

Уравнения (13.51а) и (13.51б) – векторные. Каждое из них распада-

ется на три скалярных, связывающих между собой проекции векторов

и  на оси декартовой системы координат:

и 0,

iai i



 

(13.52)

где

,,.ixyz

Отметим, что с использованием векторного магнитного потенциала

существенно упрощается вычисление магнитного потока. Действитель-

но,

rot .

dd 



Bs As

Теорема Стокса позволяет преобразовать по-

верхностный интеграл в контурный, который вычислять гораздо проще:

172









(13.53)

Здесь напрашивается чисто формальное сопоставление с законом пол-

ного тока (13.1а): линии вектора

А охватывают магнитный поток по-

добно тому, как линии вектора

Н охватывают ток.

Общей задачей расчета магнитного поля постоянных токов являет-

ся определение вектора напряженности магнитного поля или вектора

магнитной индукции в каждой точке пространства по заданному рас-

пределению тока. Эта задача решается определением векторного потен-

циала как функции координат. Если сравнить уравнения Лапласа–

Пуассона (13.13) и (13.15) для электростатики с уравнениями (13.51а,

б),

то легко заметить их очевидное сходство. Продолжая аналогию, можно

частному решению для распределенных по объему зарядов из (13.31)

сопоставить соответствующее выражение для проекции векторного по-

тенциала:











где R – расстояние от элемента объема dV с током до точки, в которой

определяется

Если ток I протекает по проводнику, размеры попе-

речного сечения которого S значительно меньше, чем расстояние R, то

после замены

dV Sd Id



д ll

можно найти векторный потенциал, со-

здаваемый током такого провода длиной l:









(13.54)

Кстати, из этого соотношения с учетом формулы (13.47) следует

известный из курса физики закон Био–Савара:





Hl1

(13.55)

Здесь

– единичный вектор, направленный вдоль R от элемента тока в

рассматриваемую точку.

В областях, не занятых током, более простым может оказаться ре-

шение уравнения Лапласа для скалярного магнитного потенциала

(13.49) с последующим использованием формулы (13.48). Разумеется,

для этого подходят все методы, рассмотренные при исследовании элек-

тростатического поля.

Для выбора нужного решения уравнений в

частных производных

нужно знать граничные условия, в первую очередь на поверхности раз-

дела сред с различными магнитными свойствами.

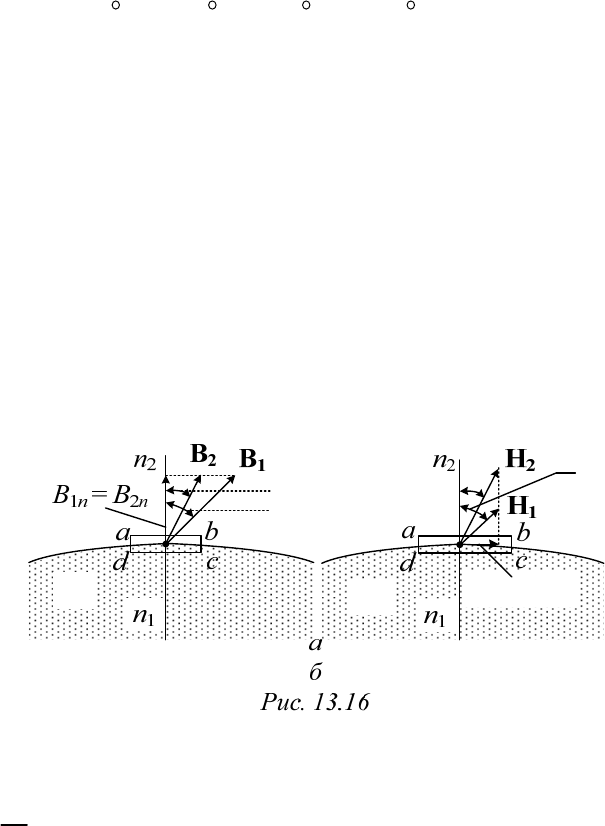
173

13.4.2. Граничные условия на поверхности раздела двух сред

с различными магнитными проницаемостями

Выделим на поверхности раздела двух сред с различными магнит-

ными свойствами точку и рассмотрим магнитное поле вблизи нее. Как

это было сделано в разделах 13.2.3 и 13.3.2, окружим эту точку цилин-

дрической замкнутой поверхностью, высота которой гораздо меньше

диаметра оснований. На рис. 13.16, а контур abcda – это след цилиндра

в плоскости чертежа, проходящей через

его ось. Вычислим магнитный

поток сквозь эту поверхность

и воспользуемся принципом непре-

рывности (13.4а). Учитывая соотношение размеров цилиндра, потоком

сквозь боковую поверхность

можно пренебречь, подсчитав лишь по-

ток сквозь поверхности оснований

21о

SSS



21оц











SSSS

dddd sBsBsBsB

Будем полагать и поверхности оснований столь малыми, что в их

пределах векторы

иBB

не меняются, тогда интегралы от скаляр-

ных произведений с учетом расположения векторов по отношению к

нормали

перейдут в равенство:

22 2 11 1

cos cos 0.BS BS







Отсюда



(13.56)

Итак, в точке, лежащей на поверхности раздела двух сред с раз-

личными магнитными проницаемостями, нормальные составляющие

вектора магнитной индукции равны.

Теперь окружим ту же точку прямоугольным контуром abcda в

плоскости чертежа (рис. 13.16, б) и воспользуемся формулой (13.1а), со-

хранив соотношение

.ab cd bc da

Получим

abcda ab cd ab

dd dd



 



Hl H l H l l



 

Здесь введена вели-

чина



 линейная плотность поверхностного тока, который

1а



2а





1а



2а









174

направлен перпендикулярно плоскости чертежа. Чтобы осмыслить это

понятие, представим себе однослойную обмотку с током I и числом

витков w, охватывающую часть ферромагнитного сердечника высо-

той h. При этом и диаметр провода, и толщина изоляции малы по срав-

нению с размерами сердечника и с высотой h. Тогда можно считать, что

ток течет как

бы тонким слоем по поверхности сердечника и его линей-

ная плотность примерно равна





Если же полагать и отрезки ab, и cd столь малыми, что в их преде-

лах векторы

иHH

не меняются, то интегралы от скалярных про-

изведений с учетом расположения векторов по отношению к нормали

перейдут в равенство:

2211

sin sin .

cd H ab ab









Отсюда

.HH









(13.57а)

В точке, лежащей на поверхности раздела двух диэлектриков, ка-

сательные составляющие вектора напряженности магнитного поля

отличаются на величину линейной плотности поверхностного тока.

Если же этот ток отсутствует, то

0.HH







(13.57б)

В таком случае справедливо и соотношение









(13.58)

Отсюда ясно, что если магнитная проницаемость одной из сред го-

раздо больше магнитной проницаемости другой (например,





то из второй среды в первую линии вектора магнитной индукции будут

входить в первую под прямым углом. Поэтому можно считать, что по-

верхность ферромагнитной среды имеет во всех точках один и тот же ска-

лярный магнитный потенциал. Значит, при исследовании магнитного поля

в воздухе

()





вблизи сердечника из электротехнической стали

()





можно применять метод зеркальных изображений. Если в

воздухе имеются проводники с токами, которые и создают магнитное по-

ле, то для его расчета на место зеркальных изображений нужно поместить

проводники с токами того же направления, что и в реальной области.

13.4.3. Расчет магнитных полей в областях с простой геометрией

Пример 13.13. Поле кругового контура с током (рис. 13.17)

Известны радиус контура

и ток в нем I.

Определить напряженность магнитного поля

Н, скалярный



векторный

А магнитные потенциалы на оси контура в точке, отстоящей

на расстояние z от плоскости витка.

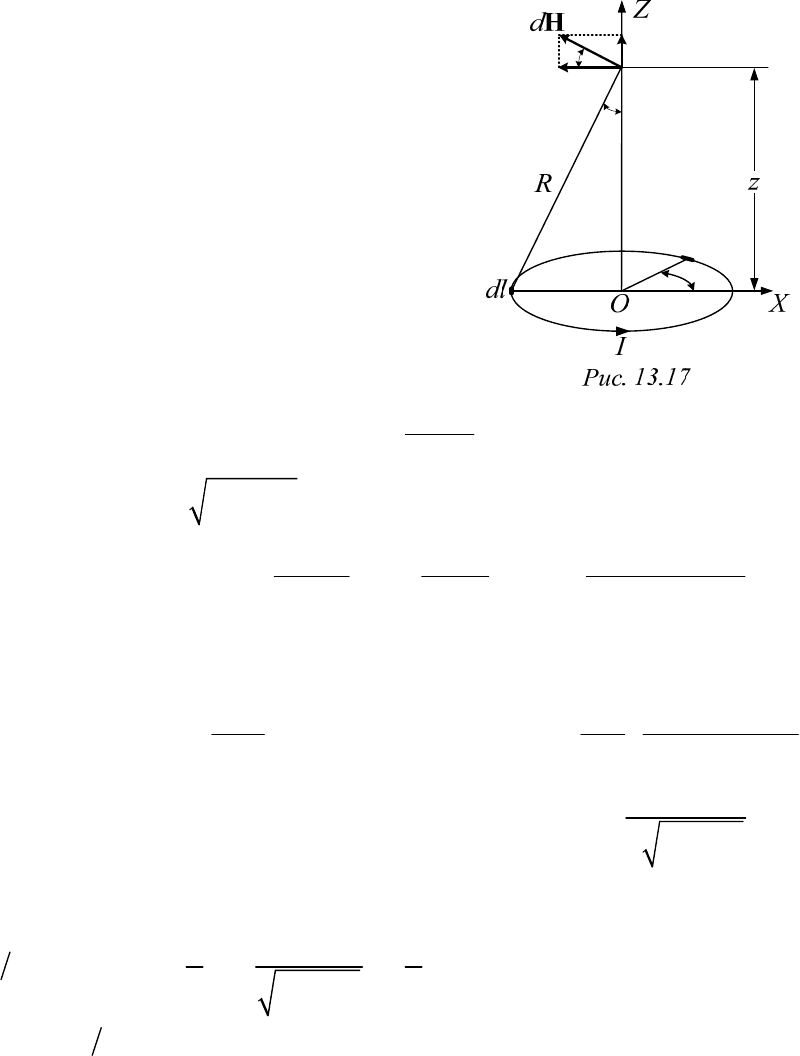
175

Решение

Для определения напряженности ис-

пользуем закон Био–Савара. Из формулы

(13.55) следует, что составляющая вектора

напряженности магнитного поля d

H на

оси контура от элемента тока Id

l лежит в

плоскости, проходящей через эту ось. По-

этому при суммировании составляющих

от всех элементов контура горизонталь-

ные проекции

уничтожат друг друга,

а вертикальные

будут складываться

арифметически. В рассматриваемой точке





sin sin ,

Idl

dH dH







00 0

где ,,sin/.dl r d R r z r R



 

23 223/2

sin

Поэтому .

44 2()

Ir Ir

HdH dl d

RR rz









  





Поскольку вектор напряженности

Н направлен вдоль оси, то его

величина согласно (13.48) связана со скалярным магнитным потенциа-

лом формулой



 Тогда

223/2

()

Hdz



 





Этот табличный интеграл приводится к виду:







где



постоянная интегрирования. Если полагать





при



то

2,DI

тогда



11cos.

IzI









 







В центре витка (при

0)z 





Формула (13.54) говорит о том, что составляющая векторного маг-

нитного потенциала d

А от элемента тока Idl направлена также, как век-

тор d

l. Поэтому, очевидно, интегрирование по контуру даст для точек,

лежащих на оси витка, результат



176

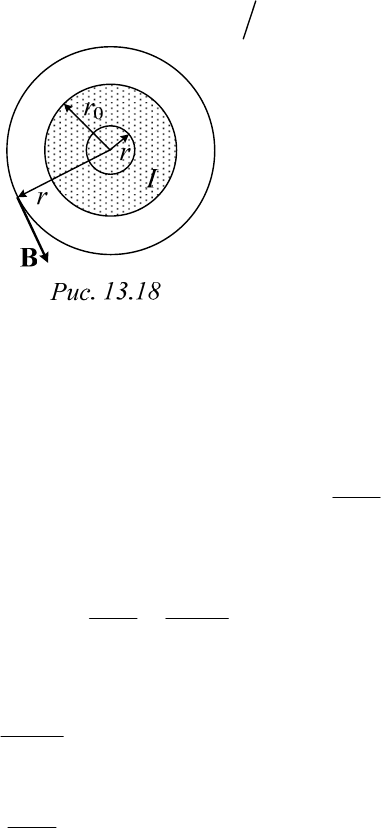
Пример 13.14. Поле бесконечно длинного прямолинейного цилиндрическо-

го проводника кругового сечения с постоянным током

Известны радиус проводника

, ток I, магнитные проницаемости

материала проводника



и окружающей среды



Определить вектор магнитной индукции

В и векторный магнитный

потенциал

А внутри и вне провода, а также скалярный магнитный по-

тенциал (вне провода).

Решение

Магнитное поле – плоскомеридианное. Ось OZ цилиндрической си-

стемы координат перпендикулярна плоскости чертежа на рис. 13.18. Ток

распределяется равномерно по сечению проводника. Вектор плотности

тока направлен вдоль оси OZ, его величина

().







В силу симметрии системы, вектор напряженности Н направлен по

касательной к окружности с центром в начале координат, а его значение

не зависит от угловой координаты



. Тогда по закону полного тока

(13.1а) для точек вне проводника (контур радиуса

)rr

имеем

2,откуда .

IdHrd rH H







  





При

rr

контур интегрирования охватывает лишь часть тока

(/ ).

rIrr





Поэтому





Значения вектора магнитной индукции внутри и вне проводника:

,при









(13.59а)

.при

B 







(13.59б)

Поскольку вектор магнитной индукции имеет в цилиндрической

системе координат лишь одну составляющую

,BB





то, раскрыв вы-

177

ражение

rot A

в этой системе, найдем .









Так что и векторный

магнитный потенциал имеет тоже одну составляющую

A

Внутри проводника

Bdr rdr C







   







Снаружи

ln .

Bdr r C





   



Если принять значение векторного магнитного потенциала на по-

верхности проводника

()rr

равным нулю, то легко можно найти по-

стоянные интегрирования:

120

,ln.

CCr





 Тогда

,при1























(13.60а)

.приln

A 







(13.60б)

Линии вектора магнитной индукции одновременно являются лини-

ями равного векторного потенциала и подчиняются условию

const.r 

Значит, они представляют собой концентрические окружности, лежа-

щие в плоскостях, перпендикулярных оси проводника.

Скалярный магнитный потенциал найдем, раскрывая выражение

grad H

в цилиндрической системе координат (опять же учитывая нали-

чие лишь одной составляющей вектора магнитной индукции

):HH

















Напомним, что понятие скалярного магнитного потенци-

ала имеет смысл лишь в областях, незанятых током, т. е. вне проводни-

ка. Поэтому

rd d D







   



Можно принять

мм

0 при 0, тогда 0 и (2 ).DI





 

Плоскости равного скалярного магнитного потенциала проходят

через ось проводника, подчиняясь условию

const.





Скалярный маг-

нитный потенциал многозначен даже при вполне определенной плоско-

сти нулевого потенциала. Действительно, выбирая контур интегрирова-

ния, n раз охватывающий провод, получим добавку к



в виде nI. Что-

бы этого избежать, условливаются не пересекать при выборе этого кон-

тура плоскость нулевого скалярного потенциала.

178

Пример 13.15. Магнитное поле двухпроводной линии

Известны ток линии I, расстояние между проводами линии d, их

радиусы

, магнитные проницаемости среды



и материала прово-

дов



Определить скалярный



и векторный А магнитные потенциалы.

Решение

Воспользуемся принципом

наложения. Результаты, получен-

ные в предыдущем примере, легко

позволяют это сделать. Если со-

провождать индексом 1 составля-

ющие величин, относящиеся к то-

ку, направленному вдоль оси OZ, а

индексом 2 относящиеся к току,

текущему в противоположном

направлении, то в некоторой точ-

ке Р (рис. 13.19), лежащей вне

проводов

, окажется

мм1 м 212

(ln ln ) ln ,

[( )] .

AA r r D D





   





   





    

Здесь

иrr

расстояния от точки Р до осей проводов,

иDD





постоянные интегрирования.





углы в тре-

угольнике между осью абсцисс и отрезками

и ,rr

тогда

().





 

Если принять



в начале координат, где

,rr





на оси абсцисс правее первого провода, где





то формулы

принимают вид:

ln ,







(13.61)







 (13.62)

Если в уравнении (13.61) заменить

на ,





ана,A



то получится формула для потенциала электрического поля двух разно-

именно заряженных осей (13.26). Значит, уравнение линии равного век-

торного потенциала то же самое (13.62), а сама линия представляет со-

бой окружность, центр которой лежит на оси абсцисс. Одновременно,

179

как было показано при обсуждении примера 13.14, эта линия является

линией магнитной индукции (и напряженности магнитного поля).

В свою очередь уравнение (13.62) при

const





описывает окружность,

проходящую через оси проводов. Ведь, как известно, вписанный угол



не меняется при перемещении точки по окружности.

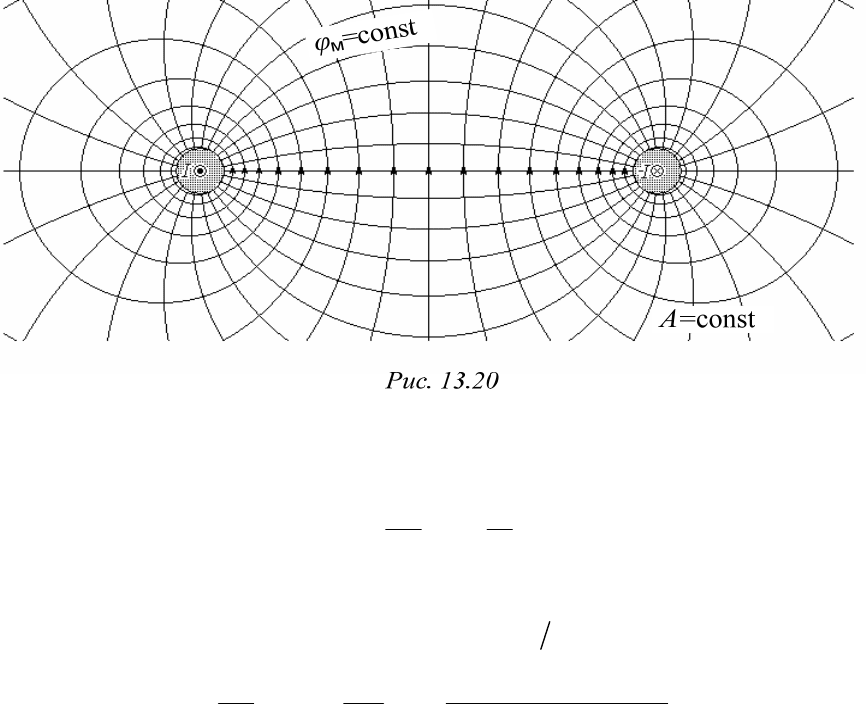
Таким образом, картины электрического и магнитного полей двух-

проводной линии, у которой расстояние между проводами гораздо

больше их радиуса, практически одинаковы. Но линии напряженности и

линии равного потенциала меняются местами (рис. 13.20). Разница в

том, что в электростатическом поле линия равного электрического по-

тенциала

совпадает с поверхностью провода, а в магнитном одна из ли-

ний напряженности магнитного поля лишь касается его поверхности.

Дело в том, что электростатическое поле двух проводов было таким же,

как поле двух заряженных осей, причем эти электрические оси были

смещены относительно геометрических в направлении к началу коор-

динат. Магнитное же поле

вне проводов соответствует сосредоточен-

ным токам именно на геометрических осях.

Что касается магнитного поля внутри проводов, то по-прежнему

нетрудно записать выражение векторного магнитного потенциала, ис-

пользуя метод наложения:

2ln .























Здесь D – постоянная интегрирования, которую можно определить из

принятого выше условия



при

2.rr d



В этом случае

211

2(/2)(/2)

2ln .

rdrdr















180

Анализ этого выражения весьма обременителен и здесь не прово-

дится. Например, даже при





трудно на картине поля найти точ-

ку, в которой сходятся линии магнитной индукции и, значит,

0.B 

От-

метим лишь, что такая точка (назовем ее магнитной осью) смещена от-

носительно геометрической оси в направлении от начала координат.

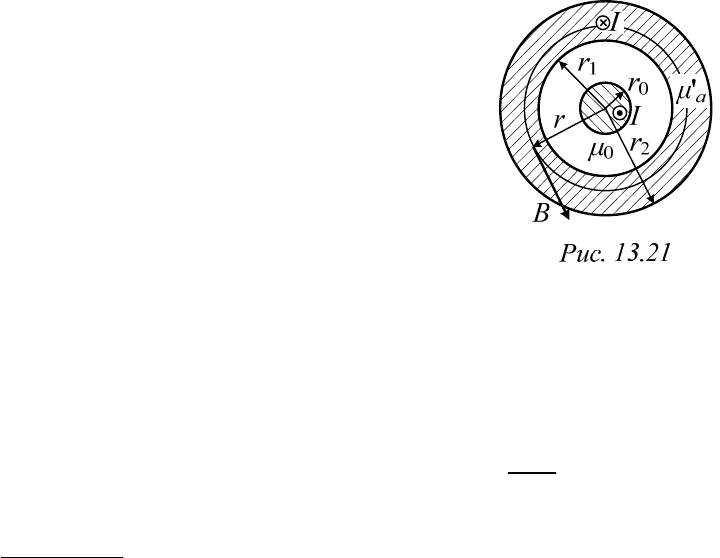
Пример 13.16. Магнитное поле коаксиального кабеля (на рис. 13.21

показано поперечное сечение кабеля)

Известны геометрические размеры кабеля и

постоянный ток I в нем. Центральный проводник

(жила кабеля), по которому ток I течет от источ-

ника к приемнику (на рис. 13.21 он направлен к

наблюдателю) имеет радиус

По наружному

трубчатому проводнику (оболочке кабеля) с внут-

енним радиусом

и внешним

ток I течет в

противоположном направлении. Абсолютные

магнитные проницаемости изоляции



жилы



и оболочки





Определить вектор магнитной индукции В и векторный магнитный

потенциал

А.

Решение

Постоянный ток по сечению проводников распределяется равно-

мерно. Величина плотности тока в толще жилы







а в теле обо-

лочки

()









причем векторы

направлены в проти-

воположные стороны. Законы изменения искомых величин различны в

четырех областях: 1) в центральном проводнике, 2) в диэлектрике между

проводниками, 3) в теле наружного проводника и 4) за пределами кабеля.

В двух первых областях в силу симметрии системы и в согласии с

законом полного тока поле ничем не отличается от поля цилиндриче-

ского проводника с током. Соответствующие формулы для

,BB

(13.59а, 13.59б) и

,AA

(13.60а, 13.60б) получены в примере 13.14.

При исследовании поля в третьей области воспользуемся методом

наложения. Вычтем из величины составляющей, обусловленной током в

центральном проводнике, составляющую, созданную той частью тока

наружного проводника

(),





которая протекает внутри

трубки, ограниченной окружностью радиуса r. Для определения состав-