Эськов В.Д., Каталевская А.В. Теоретические основы электротехники. Часть 2

Подождите немного. Документ загружается.

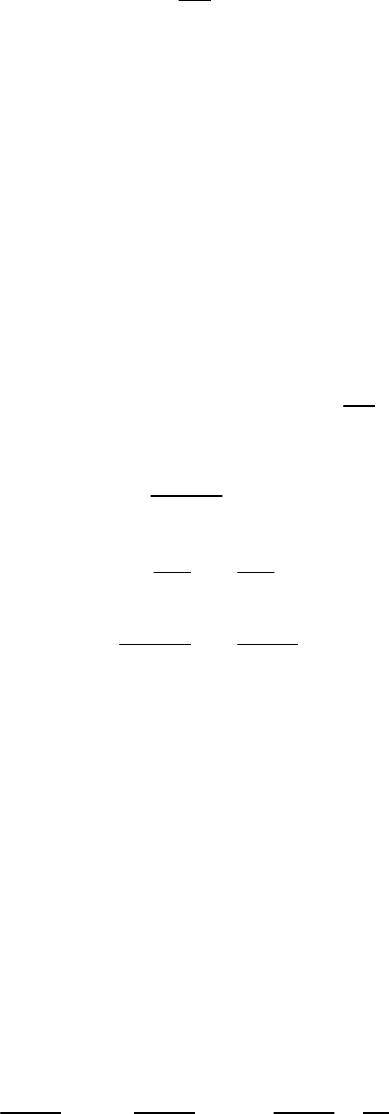
151





Если эта величина постоянна

(const),





то в силу симметрии поля

и потенциал, и напряженность поля зависят лишь от радиальной коор-

динаты цилиндрической системы. Поверхности равного потенциала

представляют собой коаксиальные цилиндры, а линии напряженности –

радиальные прямые. Окружим отрезок оси длиной l соосным цилин-

дром радиуса r (в сечении, перпендикулярном оси, это выглядит также,

как показано на

рис. 13.2, а) и воспользуемся теоремой Гаусса (13.3б).

Поток вектора напряженности сквозь поверхности оснований равны ну-

лю, поскольку вектор касается этих поверхностей. Поэтому остается

лишь поток сквозь боковую поверхность цилиндра

2:Srl





цбб

2.Отсюда

SSS

ddEdsESErl











Es Es











(13.24)

Из формулы (13.12) следует

dn dr



  тогда

ln .

dr r A





 

   



(13.25)

Следует иметь в виду, что в данном случае нельзя принять равным

нулю потенциал бесконечно удаленных точек. Должно быть дополни-

тельное условие в задаче (например, соответствующее

0).



13.2.6.2. Применение принципа наложения

Пример 13.4. Поле двух параллельных бесконечно длинных осей

Пусть оси (рис. 13.3) находятся на расстоянии 2b друг от друга и

имеют одинаковые по величине, но противоположные по знаку заряды,

равномерно распределенные по длине

(const).





Для того, чтобы опре-

делить потенциал любой точки поля, воспользуемся принципом нало-

жения и формулой (13.10), полагая в ней



Получим:

ln ln ln .

22 2

aa a







  

  

(13.26)

Здесь

иrr

расстояния от заряженных осей до рассматрива-

емой точки. Уравнение линии равного потенциала

/ const.rr k



(13.27)

152

В частности, плоскость





равноудалена от обеих осей

().rr

Из курса математики известно, что геометрическое место точек,

удовлетворяющих условию (13.27), – это окружность, центр которой ле-

жит на прямой, проходящей через оси. Расстояние от центра до плоско-

сти нулевого потенциала s и радиус окружности R определяются значе-

нием параметра семейства эквипотенциальных линий k. Можно пока-

зать [2], что между собой эти величины

связаны простым соотношением:







(13.28)

При заданной величине параметра k отсюда можно найти R и s.

И наоборот, зная геометрические размеры, легко можно подсчитать

значение k, а затем и потенциал.

Окружности, соответствующие

1,k 

расположены слева от плоско-

сти, где





поэтому



А при

1,k 

окружности окажутся справа от

плоскости нулевого потенциала

(0).



В свою очередь линии напря-

женности представляют собой дуги

окружностей, которые проходят че-

ез оси. Их центры лежат в плоскости

нулевого потенциала. Две такие ли-

нии, вместе составляющие окруж-

ность, также показаны на рис. 13.3.





const













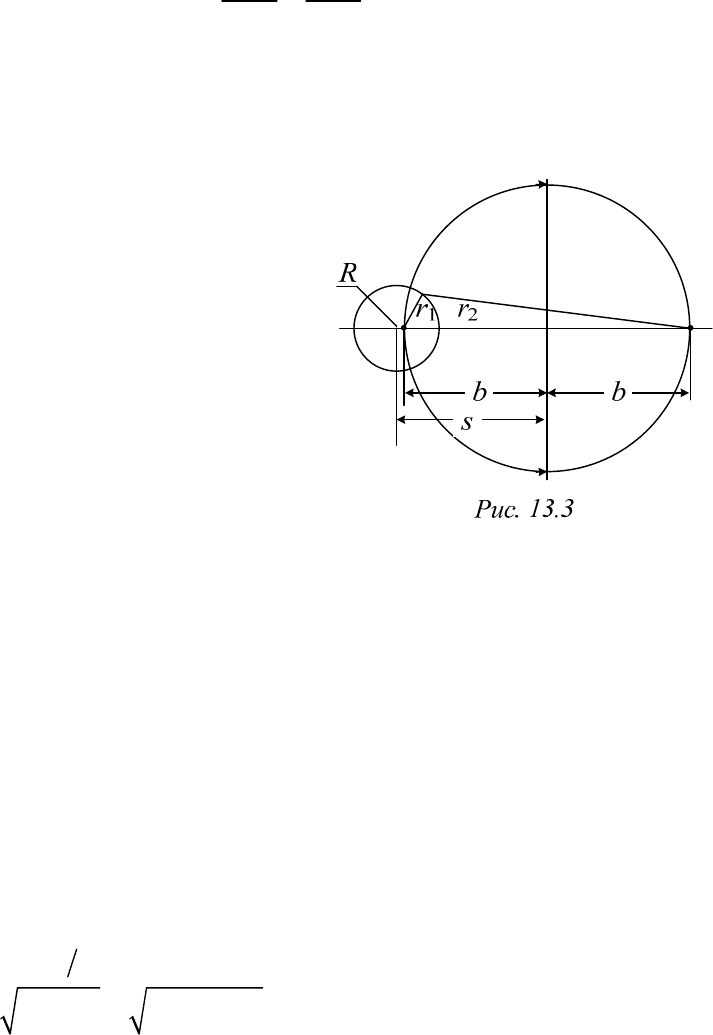
Пример 13.4. Поле двухпроводной однородной линии

Пусть известны радиусы проводов

расстояние между их

осями d и заряды проводов на единицу длины 



. Первое следствие из

теоремы единственности позволяет утверждать, что поле такой линии

аналогично полю двух разноименно заряженных осей. Нужно только

определить положение этих электрических осей относительно плоско-

сти нулевого потенциала. А то, что они лежат на линии, проходящей

через геометрические оси проводов, не подлежит сомнению.

Если перейти к обозначениям предыдущего примера,

то заданы ра-

диусы двух симметрично расположенных эквипотенциалей

Rr

расстояния

d

от их центров до плоскости





Тогда из (13.13)

следует:

22 2 2

/4 .bsr d r 

153

Чтобы определить потенциалы проводов, нужно вычислить значе-

ния параметров семейства эквипотенциальных линий, соответствующих

поверхностям проводов. Тогда из (13.2б) с учетом (13.28) получим:

ln ln ln 1 .

22 22

aa a

db d d

 



  











  









(13.29)

Знак «плюс» в этой формуле относится к положительно заряжен-

ному проводу, «минус» – к отрицательному. Напряжение между прово-

дами

2.U





Картина поля двухпроводной линии показана на рис. 13.4. Чтобы

поток вектора напряженности электрического поля был одинаков в

каждой трубке поля, соседние линии напряженности (мысленно про-

долженные внутрь проводов) должны вблизи электрических осей обра-

зовывать равные углы. Чтобы обеспечить выполнение условия

const,







  

нужно обеспечить постоянство отношения

/ const.

















const





Заметим в заключение, что уже упоминавшееся следствие из тео-

ремы единственности позволяет перенести решение примера 13.3 на за-

дачи об электростатическом поле двух параллельных несоосных цилин-

дров разных диаметров.

13.2.6.3. Непосредственное интегрирование уравнения Лапласа

Оно может быть легко выполнено, если, как и в приме-

рах 13.1 и 13.3, потенциал зависит лишь от одной координаты и заданы

граничные условия.

154

Пример 13.5. Поле коаксиального кабеля

Известны радиус

внутреннего цилиндрического

проводника (жилы кабеля) и внутренний радиус

наруж-

ного проводника (оболочки кабеля), потенциалы этих про-

водников соответственно U и 0, а также абсолютная ди-

электрическая проницаемость изоляции



(рис. 13.5).

Определить потенциал и напряженность электростатического поля

в диэлектрике, а также заряд единицы длины жилы кабеля.

Решение

В силу симметрии потенциал зависит лишь от радиальной коорди-

наты цилиндрической системы. В этом случае в уравнении Лапласа

остается только одно слагаемое:

()0.

rdr dr





Дважды проинтегриру-

ем это выражение. Сначала получим





затем

ln .







Используем граничные условия:

ln , ln 0.

rr rr

Ar BU Ar B





 

Отсюда

,ln),/ln(/

110

rABrrUA





так что

ln( / )





Тогда

ln( / )

dr r r r



 

(13.30а)

На поверхности жилы

()rr



граничное условие







поз-

воляет подсчитать заряд единицы длины кабеля

2.rd r











Поэтому

2/ln(/).

Urr







(13.30б)

Тот же результат можно было получить, используя теорему Гаусса

(как в примере 13.3) и первое следствие теоремы единственности, что

легко проверить.

13.2.7. Определение потенциала по заданному распределению зарядов

Эта задача решается с помощью метода наложения с использова-

нием результата, найденного в предыдущем разделе при расчете поля

точечного заряда.

Пусть задано распределение зарядов в некоторой системе тел с из-

вестной геометрией, часть из которых показана на рис. 13.6.

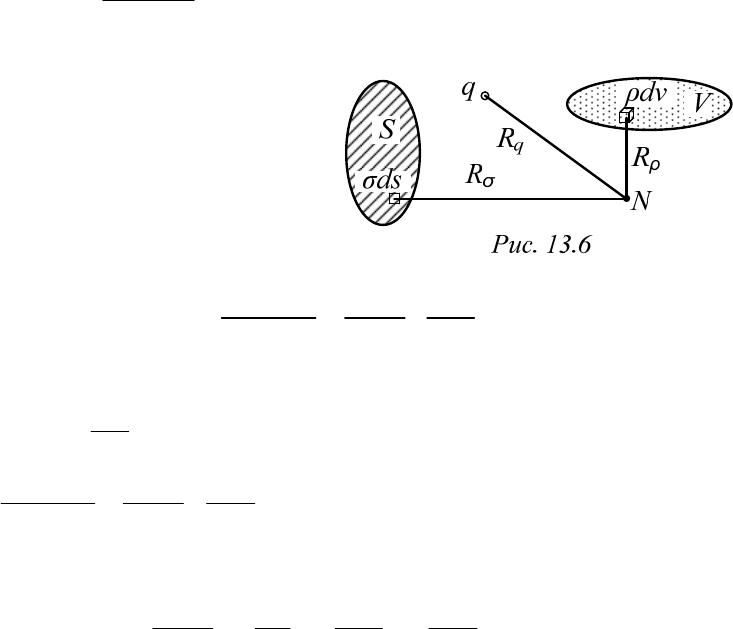
155

Если среди них есть тела, которые можно рассматривать как точеч-

ные, то потенциал в произвольной точке N можно найти по формуле

(13.8), просуммировав составляющие от действия каждого заряда в от-

дельности:







Если в систему входят прово-

дящие тела с зарядом, распределен-

ным по поверхности, то, выделив на

поверхности каждого элемент ds

с зарядом

,dq ds





можно опре-

делить составляющую потенциала

посредством интегрирования:

dq ds





 





Если в некоторой области известно распределение объемной плот-

ности заряда



 то интегрирование придется выполнить по объе-

му:

dq dv





 





Остается просуммировать найденные выше решения, тогда

qdsdv

RR R

































(13.31)

Фактически это общее решение уравнения Лапласа–Пуассона.

13.2.8. Метод зеркальных изображений

Метод основан на втором следствии теоремы единственности и

применяется для расчета поля заряженных тел, расположенных вблизи

границы раздела двух сред, имеющей правильную форму (плоскость,

цилиндр, сфера). Рассмотрим принцип расчета на примере плоскопа-

раллельного поля заряженного тела вблизи проводящей плоскости.

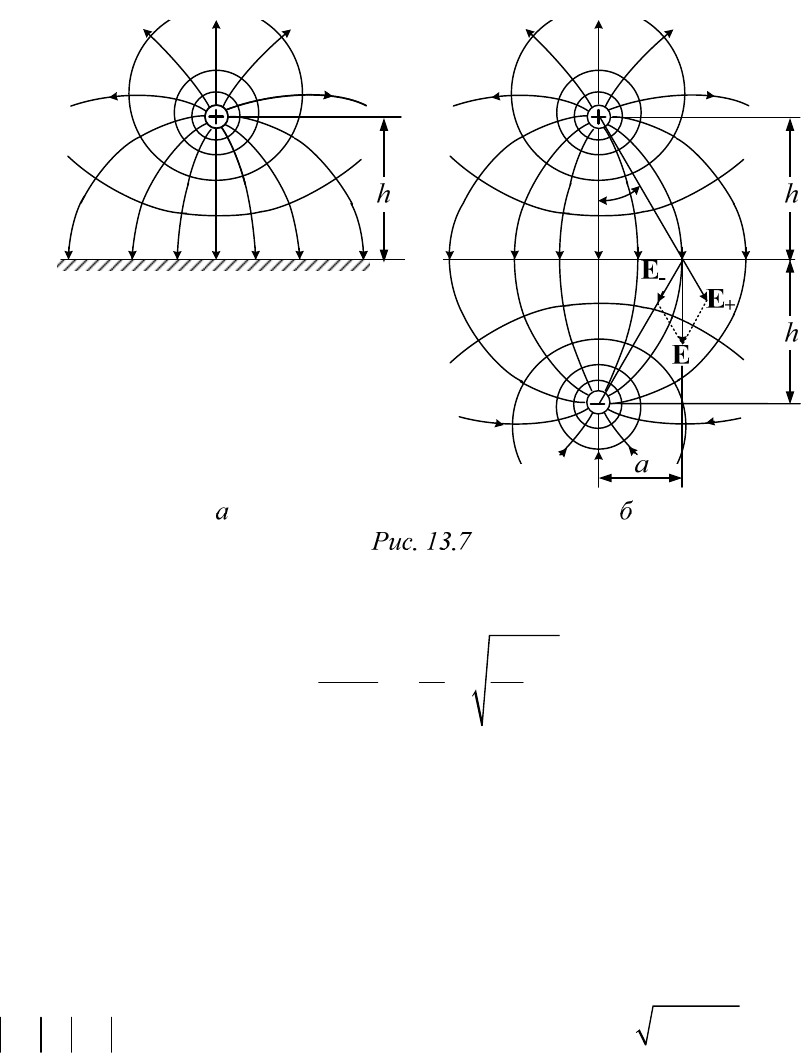
Пример 13.6. Поле прямолинейного провода над землей

Известна линейная плотность заряда  провода с радиусом

, рас-

положенного на расстоянии h от земли, чью поверхность будем считать

плоской (рис. 13.7, а).

Определить потенциал провода и распределение индуцированного

заряда по поверхности земли.

156

Решение

Очевидно, картина электростатического поля в воздухе будет такой

же, как в верхней полуплоскости системы двух параллельных проводов

с одинаковыми зарядами противоположного знака (рис. 13.7, б), по-

скольку граничные условия на плоскости нулевого потенциала одина-

ковы в обеих задачах. А решение последней уже найдено в приме-

ре 13.4.















В частности, после замены в формуле (13.29) d на 2h получим зна-

чение потенциала провода:

ln 1 .

























(13.32)

Чтобы выяснить распределение индуцированного заряда по по-

верхности земли, воспользуемся граничным условием на поверхности

раздела проводника и диэлектрика (13.21):

,DE







причем векторы

E и D нормальны к поверхности земли. Найдем величину E в точке, от-

стоящей от проекции оси на расстоянии a (рис. 13.7, б), методом нало-

жения, сложив составляющие напряженности электрического поля от

действия реального и фиктивного зарядов. Каждая из этих составляю-

щих может быть вычислена по формуле (13.24):

/(2 ),







EE

где в данном случае

.rah При сло-

жении векторов

и E

–

их касательные составляющие

sin







157

уничтожают друг друга, а нормальные

cos /

na a

EEhr





удваива-

ются. Поэтому

222

()

rah



 



  



Таким образом, чтобы рассчитать поле заряженного тела в диэлек-

трике вблизи плоской границы с проводящей средой, нужно заменить

проводящую среду диэлектрической и разместить в ней зеркальное

изображение этого тела с зарядом той же величины, но противополож-

ного знака. При этом тело может иметь любую форму (разумеется, поле

тогда может не

быть плоскопараллельным). Метод применим и при

наличии нескольких заряженных тел. Только каждое из них взамен про-

водящей среды должно получить свое зеркальное изображение с пере-

меной знака заряда. А затем следует использовать метод наложения.

Метод зеркальных изображений может быть использован и в том

случае, когда диэлектрик ограничен двумя проводящими плоскостями,

сходящимися

под углом







где n – целое число. При этом, кроме

реального заряженного тела, появятся несколько зеркальных изображе-

ний с одинаковыми зарядами и чередующимися знаками.

Например, при расчете поля провода вблизи прямого двугранного

угла, образованного проводящими плоскостями

(2),







заданную си-

стему можно заменить четырьмя проводами в однородном диэлектрике

(рис. 13.8).

















Применение метода зеркальных изображений упрощает процедуру

расчета поля и вблизи границы раздела двух диэлектриков [2].

13.2.9. Метод сеток

Этот численный метод основан на замене дифференциальных

уравнений поля уравнениями в конечных разностях. При этом рассчи-

тываются конкретные значения функции потенциала в дискретных точ-

ках области – в узлах, система которых образует сетку. Для каждого уз-

ла сетки записывается уравнение. Полученная таким образом система

линейных алгебраических уравнений содержит большое количество не-

158

известных. Поэтому применение для ее решения определителей, после-

довательного исключения неизвестных, обращения матриц нецелесооб-

разно. Вместо этого используются те или иные итерационные методы

решения.

Рассмотрим принцип расчета на примере плоскопараллельного по-

ля, хотя метод может быть использован и для расчета трехмерных по-

лей. Заданная область мысленно покрывается сеткой, обычно равно-

мерной

с квадратными ячейками. Сетка располагается таким образом,

чтобы крайние ячейки по возможности удачно вписывались в границы

рассматриваемой области. Шаг сетки h (длина стороны ячейки) выбира-

ется в соответствии с требуемой точностью расчета.

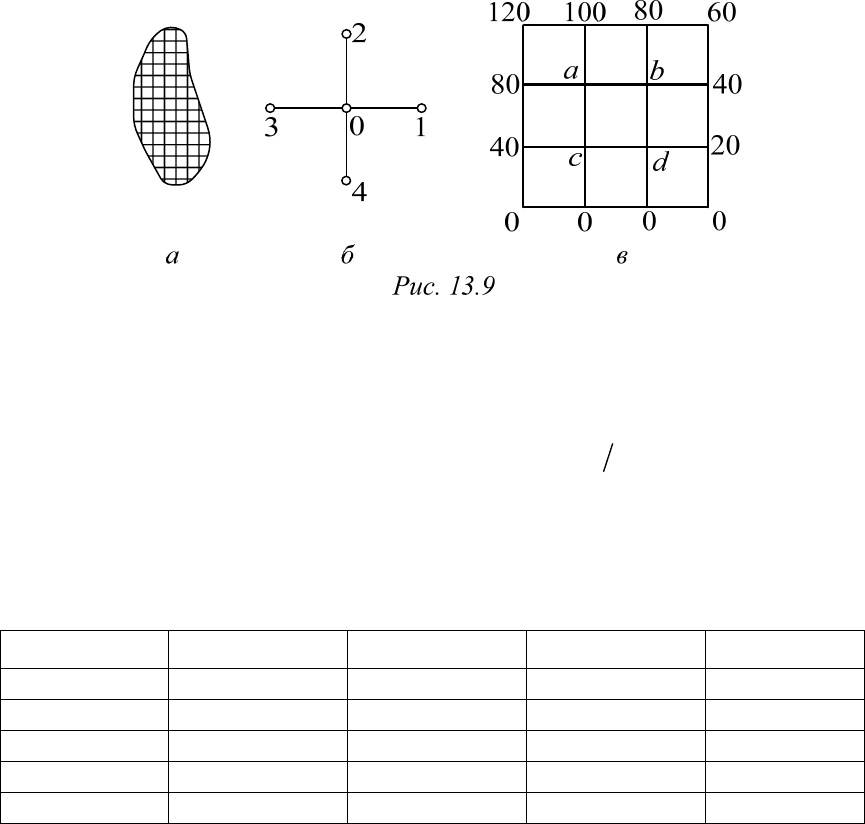
Предположим, что в заданной области, ограниченной плоской кри-

вой, нет зарядов (рис. 13.9, а), тогда для любой внутренней точки

спра-

ведливо уравнение Лапласа:







  



Заменим в этом уравнении бесконечно малые величины конечными

разностями. Для любого внутреннего узла сетки будет справедлива сле-

дующая запись:

()

() ()











где



 

Здесь прира-

щение потенциала вдоль оси абсцисс около данного узла сетки





вы-

числяется дважды: слева и справа от рассматриваемого узла. Соответ-

ственно, приращение потенциала вдоль оси ординат





подсчитыва-

ется тоже два раза: сверху и снизу от того же самого узла. А затем под-

считываются разности этих приращений

()





().





Напри-

мер, для узла 0, окруженного узлами 1, 2, 3, 4 (рис. 13.9, б), получим:

левая разность







правая разность









горизонтальная разность

13 0

() 2,



 





верхняя разность







нижняя разность









вертикальная разность

24 0

() 2.



 





Подстановка этих величин в разностное уравнение дает:

13 0 13 0

0, откуда





 



01234

()4.



 



(13.33)

С помощью этой формулы организуется циклический вычисли-

тельный процесс. Вначале потенциалы внутренних узлов задаются про-

извольно (нулевое приближение). Затем в соответствии с выбранным

159

порядком обхода внутренних узлов принятые значения уточняются по

формуле «одной четвертой» (13.33) – это первое приближение. По этим

значениям вычисляется второе приближение и т. д. Процесс повторяет-

ся до тех пор, пока отличие значений потенциалов узлов в двух после-

дующих приближениях не окажется меньше заданной точности расчета.

Пример 13.9. Расчет распределения потенциала методом сеток

Известно распределение потенциала (в вольтах) по периметру

квадратной области (рис. 13.9, в).

Определить потенциалы внутренних узлов с точностью до 3 %.

Решение

Пусть в нулевом приближении

70 В,





50 В,





30 В,





30 В.





По формуле (13.33)

(50 100 80 10) 4 65 В.





 

Аналогич-

ным образом подсчитаем

111

55 В,35В,25В.

bcd









Дальней-

шие вычисления сведены в табл. 41.1, где k – номер приближения, а

значения потенциалов даны в вольтах.

Таблица 13.3



0 70 50 30 30

1 65 55 35 25

2 67,5 52,5 32,5 27,5

3 66,25 54,25 33,75 26,25

4 67 54 33,1 27

Различие чисел в третьем и четвертом приближениях начинается с

третьей значащей цифры, что вполне укладывается в заданную степень

точности.

160

13.2.10. Расчет электрических емкостей

Понятие емкости имеет строгий смысл лишь в двух случаях. Это

либо уединенное тело, тогда емкость – коэффициент пропорционально-

сти между зарядом и потенциалом тела. Либо конденсатор – система

двух тел, имеющих заряды, одинаковые по величине, но противополож-

ные по знаку. Тогда емкость – коэффициент пропорциональности меж-

ду зарядом и напряжением между обкладками.

Емкость уединенного тела вычисляется по формуле

,Cq





(13.34)

где q и



– заряд и потенциал тела, причем должна быть определена об-

ласть с потенциалом, равным нулю.

Пример 13.7. Емкость проводящего шара

Подставив в формулу (13.34) значение потенциала из выраже-

ния (13.23), получим известное соотношение







где R – радиус

шара. Обычно эту формулу используют для иллюстрации единицы из-

мерения емкости – фарады, вычисляя емкость Земли. Если принять

средний радиус Земли равным 6370 км, то ее емкость равна:

91 6

4 (4 9 10 ) 6,37 10 708 мкФ.C





    

Пример 13.8. Емкость единицы длины прямолинейного провода вблизи

поверхности Земли

Воспользовавшись формулами (13.32) и (13.34), куда вместо q сле-

дует подставить величину заряда единицы длины провода , получим:

00 0 0

2/ln/ (/)1.Chrhr











Если, как это часто бывает,

,hr

то

00 0

2/ln(2/).Chr







Емкость конденсатора вычисляется по формуле

,CqU



(13.35)

где U – напряжение между обкладками; q – заряд каждой из них.

В разделе 1 [6] по этой формуле была вычислена емкость плоского

конденсатора:

CSd





где d – расстояние между обкладками, S –

площадь каждой из них. Добавим еще несколько примеров.

Пример 13.9. Емкость единицы длины двухпроводной линии

Если расстояние до поверхности земли существенно превышает

расстояние между проводами d, то можно использовать форму-

лы (13.29) и (13.35) опять же с заменой q на



. Тогда