Егоров-Тисменко Ю.К. Кристаллография и кристаллохимия
Подождите немного. Документ загружается.


80
Кристаллография и кристаллохимия
/_
4
2
= L
6
3
= L
2
(где надстрочный индекс показывает количество поворотов
вокруг той или иной оси).
В приведенных примерах операция симметрии рассматривалась как
перемещение точек объекта относительно фиксированной координатной
системы. Однако тот же результат может быть получен путем преобразо-
вания (движения) координатной системы относительно неподвижной
исходной точки. В этом случае операция симметрии будет представлена
преобразованием координатной системы.
2.4.3.
Представление симметрических операций путем преобразования
координатной системы
Нетрудно понять, что операция преобразования координатной систе-
мы обратна операции преобразования точек объекта, и наоборот. Поэто-
му при описании преобразований симметрии объекта следует различать
два аспекта: с одной стороны, симметрия объекта может быть выявлена,
если он неподвижен и исследователь меняет систему координат, с дру-
гой — объект может быть совмещен сам с собой путем симметрических
преобразований при неподвижной координатной системе. Второй под-
ход к операциям симметрии более нагляден, но все же не позволяет, не-
смотря на тот же конечный результат, сделать обобщения.
Проиллюстрируем сказанное примером операции поворота вокруг
оси 4-го порядка (L
A г)
), совмещенной с координатной осью Z (рис.
2.27).
Вместо поворота исходной точки 1 с координатами xyz на 90° против ча-
совой стрелки в положение 2 с координатами yxz можно преобразовать
координатную систему, повернув ее в обратном направлении (по часовой
стрелке) на тот же угол вокруг этой же оси 4-го порядка. При таком по-
вороте положение оси Z не изменится, местами и знаками поменяются
две другие оси: положение старой оси X займет новая Y, новая же ось X'
окажется в положении старой - Y, т. е. X' = -
Y,
Y = X, Z' = Z. При этом
масштабные отрезки вдоль координатных осей исходного и преобразо-
ванного репера не изменятся, не изменятся и углы между соответствую-
щими осями.
Легко увидеть, что координаты исходной точки 1
(xyz),
выраженные
в новых, преобразованных осях yxz, не отличаются от координат точки 2,
полученной поворотом вокруг оси 4-го порядка. Этот же закон будет ра-
ботать и в том случае, если ось 4-го порядка направить вдоль другой оси,
например вдоль оси Y. Поворот координатной системы вокруг оси Z
4(y)
оставит без изменения координату у, тогда как координаты х и z поме-
няются местами и, соответственно, знаками, т. е. получим координаты
точки zyx.
Обобщая все сказанное, представим данное преобразование коорди-
натного репера в виде системы линейных уравнений. Для этого выразим

Глава
2.
Симметрия кристаллов
81
Рис.
2.27. К
представлению операции поворота вокруг
оси Z
путем преобразования координатной системы
единичные векторы
А,
В, С новой координатной системы
как
векторные
суммы параметров а,
Ь,
с
исходной координатной системы. Получим
си-
стему линейных уравнений:
А
=
0а-1Ь
+
0с,
Ё
=
1а
+
0Ь
+
0с,
C
=
0a
+
0b
+
ic.
Поскольку характер такого преобразования определяется лишь
ко-
эффициентами
при
единичных векторах
s,b,c
>
систему уравнений мож-
но записать сокращенно
в
виде таблицы, составленной
из
этих коэффи-
циентов,
—
матрицы
(М)
преобразования координатных осей:
г
0 1 0
Л
1 о о
0 0 1
=
(010/100/001).
Обратим внимание
на то, что при
кристаллографических преобра-
зованиях координатных систем — отражениях
в
зеркальных плоскостях
симметрии, поворотах
на
углы
60°, 90°, 120° или 180° и
инверсии
в
точ-
ке
—
координатный репер преобразуется
сам в
себя. Отсюда матрицы
соответствующих симметрических преобразований будут иметь своими
членами (коэффициентами
при
единичных векторах) нули
и
единицы.

82
Кристаллография и кристаллохимия
Это — так называемые толь-одиш-матрицы. И хотя каждая из матриц
может быть получена на основании преобразования координатной си-
стемы, она отражает соответствующее симметрическое преобразование
точек пространства. Составляя такую матрицу, мы фактически отвлека-
емся от конкретного геометрического смысла ее членов. Однако следует
иметь в виду, что члены матриц преобразования ортогональной коорди-
натной системы суть не что иное, как косинусы углов между соответству-
ющими осями новой (преобразованной) и старой (исходной) координат-
ных систем. Поэтому такую матрицу называют матрицей направляющих
косинусов. В общем случае преобразования ортогональных координатных
систем (рис.
2.28),
обычно используемых в кристаллофизике, можно
выразить системой линейных уравнений, предварительно обозначив
единичные отрезки А, В,С вдоль новых координатных осей X', У, Z'
и а,Ь,с — вдоль старых X, Y, Z:
А = а
п
•
а + а
12
•
b + а
п
-
с,
В = а,
•a + a.
n
b + а
23
•
с,
С = а.
м
•
a + a.
j2
• Ъ
+ а.,.,
•
с,
(2.4.1)
или соответствующей матрицей:
а
22
а...
где а
21
, а
22
,
а
23
—
направляющие косинусы углов между новой осью Y'
и старыми осями X, Yn
Z;
а
13
, а,
3
, а
33
—
направляющие косинусы углов меж-
ду новыми осями X', Y и Z' и старой осью Z. Первый подстрочный индекс
(г) при символе а
у
относится к новым осям, второй (/) ~ к старым. Девять
коэффициентов а
у
(где 2, 3) зависимы друг от друга и в общем слу-
чае а Ф а...
Учитывая вышесказанное, систему уравнений
(2.4.1)
можно предста-
вить в следующем виде:
А = a
•
cos X X + b
•
cos X Y + c- cos X Z,
В =
a.
•
cos Y X + b
•
cos Y Y + с
•
cos Y Z,
С = a
cosZ
X + b
cosZ
Y + c cos Z Z.
Вернувшись к рассмотренному примеру с поворотной осью 4-го по-
рядка (рис.
2.27),
вычислим единичные векторы преобразованной коор-
динатной системы:

Глава 2. Симметрия кристаллов
83
A
=
a-cos
90°
+
£-cosl80°
+
c-cos90°,
В
=
а
•
cos 0° +
Ъ •
cos 90° + с
•
cos 90°,
С
=
а
•
cos 90° +
Ь
•
cos 90° + с
•
cos 0°.
При этом матрица поворота исходной координатной системы на 90'
вокруг оси 4-го порядка по часовой стрелке будет иметь следующий вид:
'cos 90°
cos 180° cos 90°" '0 1 0'
м =
cos 0°
cos 90° cos 90°
=
1 0 0
cos 90° cos 90°
cos 0°
)
0
0 1
т. е. тот же вид, что и матрица, составленная на основании векторных
сумм (см. стр. 83).
Представление кристаллографических операций симметрии подоб-
ными таблицами направляющих косинусов во всех сингониях (см. па-
раграф
2.8.2),
как это делается в кристаллофизической практике, удобно
лишь в том случае, если и кристаллографическая координатная система
ортогональна или же она преобразуется в себя при всех операциях груп-
пы (моноклинной или триклинной сингоний). Искусственное же введе-
ние ортогонального координатного репера в гексагональную сингонию
(в присутствии осей 3-го и б-го порядков) значительно усложняет ма-
трицу направляющих косинусов, тогда как матрица преобразования кри-
сталлографической координатной системы (а = Ь^с, а =
(3
= 90°, у = 120°)
(см.
параграф 2.8), составленная на основе векторных сумм, будет иметь
по сравнению с матрицей ортогонального репера более простой вид.
Рис.
2.28. К преобразованию координатных систем

84
Кристаллография и кристаллохимия
Например, матрица поворота ортогональной координатной системы во-
круг оси
L\
(2)
на угол 120° против часовой стрелки имеет следующий вид:
1
_V3
2 2
V§
1
2 2
0 0
Такую матрицу нельзя использовать непосредственно для расчета
символов граней (см. параграф 3.1) и ребер (см. параграф 3.3) кристаллов,
вычисленных в непрямоугольной кристаллографической координатной
системе. Удобнее пользоваться матрицей, составленной на гексагональ-
ном кристаллографическом базисе (у = 120°) (см. параграф 2.8), выра-
зив,
как и в предыдущем случае, единичные векторы новой координат-
ной системы как векторные суммы единичных векторов старой системы
(рис.
2.29).
Действительно, симметрическое преобразование (поворот
вокруг оси 1?
зи)
), представленное как преобразование кристаллографи-
ческой координатной системы в векторной форме, выразится системой
уравнений:
А
=
0а
+
\Ь
+
0с,
B
=
-la-l-i
+ 0c,
C
=
0a
+
0b
+
lc.
Матрицей такого симметрического преобразования окажется «ноль-
один»-матрица:
^0 1 0
Л
110
0 0 1
которая может быть непосредственно использована и для расчета сим-
волов граней и ребер кристаллов. Таким образом, любое кристаллогра-
фическое симметрическое преобразование может быть выражено «ноль-
один»-матрицей при сохранении во всех случаях кристаллографической
координатной системы. И наоборот, любая «ноль-один»-матрица выра-
жает одну из симметрических операций. При этом если в ортогональной
координатной системе «ноль-один»-матрицы, характеризующие симме-
трические операции, содержат по одной единице в каждом столбце или

Глава 2. Симметрия кристаллов
85
U
U
Рис.
2.29. К определению матрицы поворота вокруг оси 1
ад
на угол 120'
против часовой стрелки
строке матрицы, то в гексагональной системе повороты вокруг осей 3-го
и 6-го порядков представлены «ноль-один»-матрицами, содержащими
в одной из первых строк по две ±1.
В результате к 48 ортогональным «ноль-один»-матрицам, описыва-
ющим операции симметрии кубической голоэдрии (см. параграф
6.2.1),
добавляется 16 новых (из 24) матриц гексагональной голоэдрии.
В качестве примера рассмотрим на матричном уровне последователь-
ные действия двух симметрических операций: Z
2
•
Р . Операция пово-
рота вокруг L переведет точку 1 пространства из положения xyz в поло-
жение 2 — xyz . Точка 2, будучи отраженной в горизонтальной плоскости
Р
(г)
,
займет положение 3 с координатами xyz . Первая и третья точки свя-
заны между собой результирующей операцией симметрии — отражени-
ем в точке инверсии. В итоге взаимодействие двух операций симметрии
приводит к появлению третьей, результирующей. Таким образом, мож-
но ожидать, что и на матричном уровне «взаимодействие» двух матриц
приведет к новой «ноль-один»-матрице. Действительно, каждая из рас-
сматриваемых операций может быть представлена соответствующей ма-
трицей:
/7
1 О О
Л
fl
О О
L
О 1 О
О 1 о
О 0 1 О 0 1
V
Переход от первой точки к третьей может быть осуществлен с помо-
щью результирующей операции симметрии — инверсии в точке, выра-
женной соответствующей диагональной матрицей
—
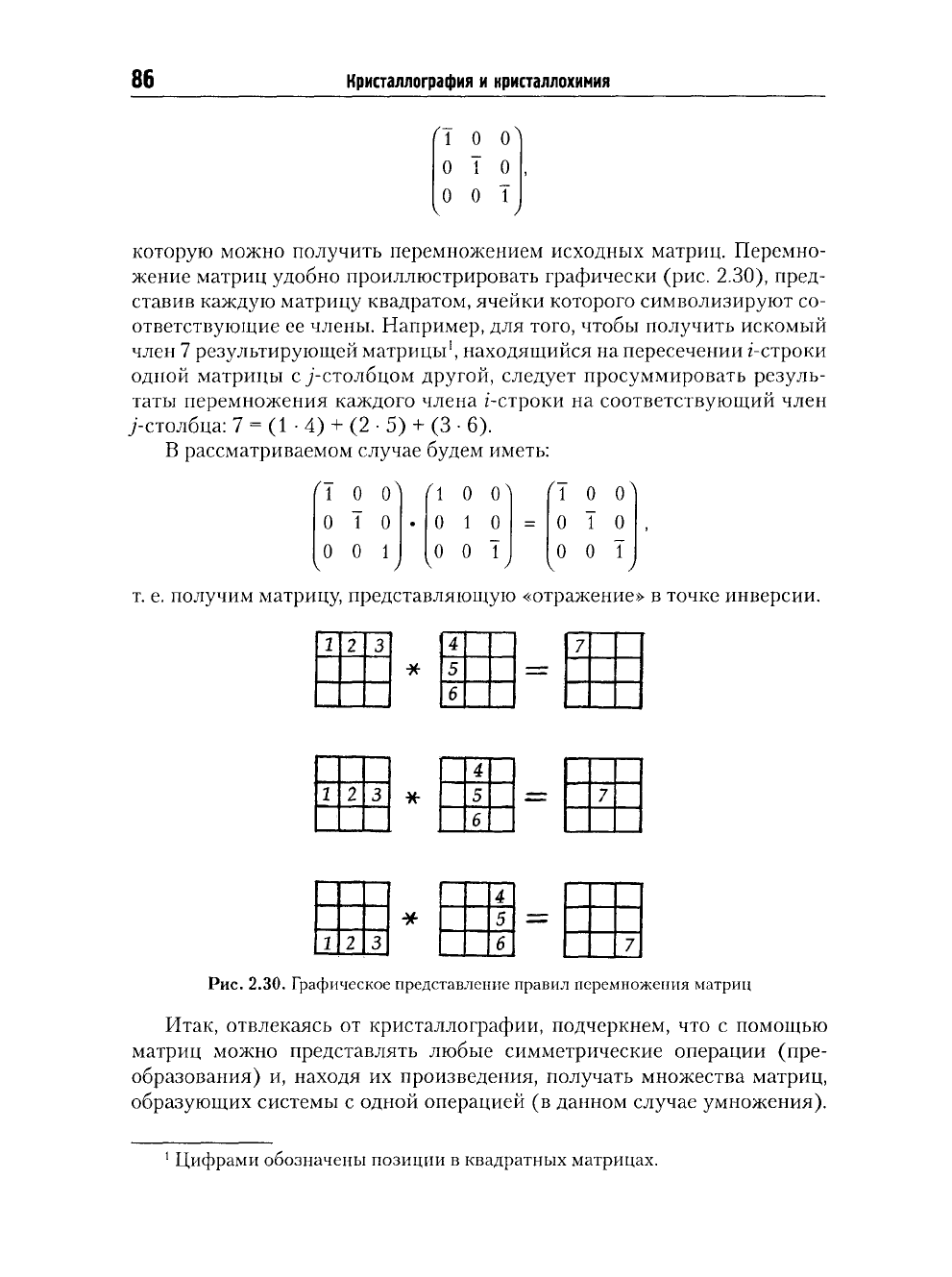
86
Кристаллография и кристаллохимия
1 О О
о Т о
о о Т
j
которую можно получить перемножением исходных матриц. Перемно-
жение матриц удобно проиллюстрировать графически (рис.
2.30),
пред-
ставив каждую матрицу квадратом, ячейки которого символизируют со-
ответствующие ее члены. Например, для того, чтобы получить искомый
член 7 результирующей матрицы
1
, находящийся на пересечении г-строки
одной матрицы cj-столбцом другой, следует просуммировать резуль-
таты перемножения каждого члена г-строки на соответствующий член
./-столбца: 7 = (1
•
4) + (2 • 5) + (3
•
6).
В рассматриваемом случае будем иметь:
'Т
0 (\ 0
0^
0 (Г
0 I 0 • 0
1
0
=
0 т 0
0
V
0
1
)
0 0
I
)
0 0
I
)
т. е. получим матрицу, представляющую «отражение» в точке инверсии.
1
2 3 7
7
4_
5]
6_
Рис.
2.30. Графическое представление правил перемножения матриц
Итак, отвлекаясь от кристаллографии, подчеркнем, что с помощью
матриц можно представлять любые симметрические операции (пре-
образования) и, находя их произведения, получать множества матриц,
образующих системы с одной операцией (в данном случае умножения).
1
Цифрами обозначены позиции в квадратных матрицах.

Глава 2. Симметрия кристаллов
87
Такие множества оказываются математическими группами (подробнее
см.
параграф 2.5).
Главной особенностью симметрических операций является то, что
полная их совокупность для любого объекта всегда образует группу.
Это позволяет рассматривать теорию симметрии кристаллов как раз-
дел математической теории множеств и использовать математический
аппарат теории абстрактных групп при изучении законов симметрии
кристаллов, придавая им конкретное геометрическое или физическое
содержание.
2.5. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ГРУПП
Теория групп к настоящему времени разработана достаточно полно,
и при изучении законов симметрии можно с успехом использовать ее по-
ложения.
Группой называется множество объектов (G) любой природы с за-
данной бинарной операцией (*), если для любой пары элементов (а и Ь)
этого множества G определен третий, результирующий элемент с = a* b
того же множества. В общем случае
a*b*b*
а. Это значит, что результат
зависит от того, в какой последовательности производится умножение
элементов группы. Применительно к операциям симметрии это означа-
ет, что результирующие операции могут оказаться различными, если по-
менять порядок выполнения исходных операций.
При этом группой будет лишь такое множество с заданной бинарной
операцией, для которого выполняются следующие условия:
• ассоциативности ~ {а * Ь) * с = а * (Ь * с);
• существования единичного члена (е)
—
такого единичного элемен-
та, что для любого элемента группы будет выполняться равенство
е*а = а*е = а;
• обратимости
—
для любого элемента а существует элемент а~
х
из
того же множества, называемый обратным элементом к элемен-
ту а, такой, что а * а~
]
= я"
1
* а = е.
Примерами групп могут быть:
1) ряд чисел с операцией сложения;
2) ряд элементов {1,-1, 7-1
>
~ V-l}
с
операцией умножения;
3) множество векторов в пространстве с операцией векторного про-
изведения;
4) совокупность операций симметрии (например, некоторого объ-
екта — {1,1 , Z,
2
, -P
(v)
}) с операцией умножения (взаимодействия
симметрических операций);

88
Кристаллография
и
кристаллохимия
5) множество матриц
с
операцией умножения
п
0 (Г
'1
0 (Г
'Т
0
<Г
'\ 0
oj
0
1
0
0
I 0 0 I
0
0
1
0
•
0 0
1
0 0
1
0
0
1
0
0
1
IV
)
V
У
)
/
Таким образом, теория абстрактных групп применительно
к
теории сим-
метрии кристаллов, по существу, является теорией групп симметрии, широ-
ко использующей математический аппарат, так как с математической точки
зрения совокупность операций симметрии удовлетворяет понятию группы,
в которой групповому умножению соответствует взаимодействие элемен-
тов симметрии (в математическом смысле элементом группы является опе-
рация симметрии,
а
не элемент симметрии, задающий эту операцию).
Группа может содержать один элемент, несколько
или
бесконечное
число отличающихся друг от друга элементов. Порядок группы
(п)
— это
число ее элементов. Группа называется конечной, если
п
конечно.
Если произведение любой пары элементов группы
не
зависит
от
по-
рядка сомножителей,
то
такая группа называется коммутативной
или
абелевой.
Если между элементами двух групп можно установить взаимно одно-
значное соответствие,
при
котором произведению любых двух членов
одной группы соответствует произведение соответствующих членов дру-
гой группы,
то
такие группы называются изоморфными. Например: груп-
пы
G
=
{g
v
g
2
,
g
3
,...
g
n
} и Н
=
{h
v
h
2
, h
y
...
h
n
}
изоморфны, т.
e. G
<-> Я, если
g
x
<->
h
v
g
2
<-^h
2
,
—
g-g-
oAA. Порядок изоморфных групп (т. е. количество
их членов) одинаков. Изоморфные друг другу конкретные группы сим-
метрии
с
точки зрения теории групп
не
различаются. Отсюда следует,
что все закономерности, установленные для одной
из
групп, справедли-
вы для всех изоморфных
с
нею конкретных групп симметрии.
В
этом за-
ключается обобщающее значение теории групп.
Изоморфные группы имеют одинаковые таблицы умножения (с точнос-
тью до перестановок). Если
в
группе G имеется такой член g, совокупность
степеней которого образует все элементы группы, т. е.
G = {g\g
2
,... = е},
то такая группа называется циклической
и ее
порядок равен
п.
При этом
элемент g., степенями которого являются все другие члены группы,
на-
зывается порождающим элементом или генератором группы.
Если
же
группа
не
циклическая,
то в
ней можно выделить несколь-
ко порождающих элементов, степени
и
произведения которых дают все
элементы группы
G.
Такая минимальная совокупность порождающих
элементов называется множеством генераторов или совокупностью
об-
разующих элементов группы. Циклические группы представляют собой

Глава 2. Симметрия кристаллов
89
степени одного генератора, и они всегда абелевы. Однако для полного за-
дания группы помимо образующих элементов необходимо знать некото-
рые соотношения между ними (например, положение относительно друг
друга),
которые называются определяющими соотношениями.
Если часть членов группы G образует относительно той же операции
группу Н, то такое подмножество Н называется подгруппой данной груп-
пы G. Например, в группе 6-го порядка
L
3
3L.
2
{L
v
L
3
X
, L.
2
, Z, , Z, ,
Z
2(u)
}
можно выделить подгруппу 3-го порядка Z
3
{L
v
Z
3
\ Lf) или подгруппы
2-го порядка L.
2
{L
v
L,
2
) и т. д.
Для конечных групп справедлива теорема Лагранжа. Порядок (г)
подгруппы (Н) является целым делителем порядка (п) группы (G), т. е.
—
=
р, где р — целое число, называемое индексом подгруппы Нв группе G
г
(или, в теории групп симметрии, кратностью правильной системы точек,
см.
параграф
6.2.5).
С другой стороны, можно сказать, что группа G является надгруппой
группы Н или что группа G является расширением группы Н.
Еще одним важным понятием теории групп являются смежные клас-
сы.
Пусть Н есть некоторая подгруппа группы G. Существует элемент g
k
группы G, не входящий в подгруппу Н (g
k
е G, g
k
<£ Н). Если умножать
этот элемент g
k
на все элементы подгруппы Н, оставляя всегда g
k
левым
сомножителем (g
k
* Н), то множество полученных значений образует
так называемый левый смежный класс относительно подгруппы Н. А по-
скольку в общем случае умножение элементов группового множества не-
коммутативно, то существует правый смежный класс относительно под-
группы Н, где элемент g
k
является правым сомножителем (Н
*
g
k
).
Очевидно, что оба смежных класса являются подмножествами груп-
пы G, так как оба класса получены перемножением элементов группы G.
Правые и левые классы в общем случае не совпадают. Если же разложе-
ние на правые и левые классы по некоторой группе Н совпадает, то такая
группа называется инвариантной или нормальным делителем.
Поскольку все закономерности сводятся к закону «умножения» эле-
ментов, структура конечной группы, ее порядок выявляется произведе-
нием любых пар ее членов, собранных в своеобразную «таблицу умно-
жения», называемую квадратом Кейли. В такой квадратной таблице
все операции симметрии, составляющие группу, записываются по гори-
зонтали и вертикали, начиная с единичного члена; произведения же их
фиксируются на пересечении вертикального столбца и горизонтальной
строки.
Например, симметрия фигуры в виде параллелепипеда (кирпича)
описывается группой симметрии
3L,
2
3PC
8-го порядка, имеющей свои-
ми членами следующие симметрические операции: Р , Р , Р
(г)
,
Z.
, L
2 )У
