Егоров-Тисменко Ю.К. Кристаллография и кристаллохимия

Подождите немного. Документ загружается.

Кристаллография

кристаллохимия

С,

(где ось

— тождественное преобразование

(Е),

играющее роль

единичного члена), наглядно выявляющиеся

на

стереографической про-

екции этой группы (рис.

2.31).

Задав точку (грань) общего положения

(см.

параграф

4.1) и

размножив

ее

всеми симметрическими операциями

данной группы, получим восемь точек общего положения, каждая пара

которых связана определенной симметрической операцией данной груп-

пы.

Пронумеровав полученные грани таким образом, что нечетные циф-

ры относятся

граням верхней полусферы, четные

—

нижней, увидим,

что грань

связана

гранью

отражением

горизонтальной плоскости

с 4

—

поворотом вокруг оси

L у

с 5

—

отражением

точке инвер-

сии С

т.

д.

>-2(х)

Рис.

2.31. К

построению квадрата Кейли для группы симметрии 3L

3PC8-ro порядка.

На стереографической проекции группы восемь точек общего положения

связаны между собой восемью операциями группы

Квадрат Кейли для указанной группы имеет следующий вид:

р<*>

Ь>

2(x>

20l)

^2{Ц

£,

2(2)

р,>

»>

Р-Цг)

^2(1)

р<»

^2(4)

р<2>

р<»>

Р<»

(

<,>

^2(2)

^2(ц)

<»

№

Р<»

2(x)

^2о;

ь>

Такая таблица дает полное представление

порядке группы

и о

том,

как взаимодействуют между собой симметрические операции,

т. е. она

определяет все

ее

члены.

Глава 2. Симметрия кристаллов

2.6. ВЗАИМОДЕЙСТВИЯ СИММЕТРИЧЕСКИХ ОПЕРАЦИЙ

(ЭЛЕМЕНТОВ СИММЕТРИИ)

Работая с кристаллами, исследователи обратили внимание на то, что

элементы симметрии располагаются в них не случайно, а определен-

ным — закономерным — образом. Действительно, сочетания элементов

симметрии, как было показано выше, и их взаимные расположения под-

чиняются всем положениям математической теории абстрактных групп.

Рассматривая взаимодействия матриц, каждая из которых отражает

определенную симметрическую операцию, можно убедиться в том, что

произведение двух матриц приводит к появлению третьей

—

результиру-

ющей — матрицы. Иными словами, произведение, или взаимодействие,

двух симметрических операций порождает третью

—

результирующую

—

операцию, а следовательно, и элемент симметрии. Рассмотрев все взаи-

модействия элементов симметрии данного кристалла, можно получить

полную совокупность симметрических операций, называемую группой

симметрии (или классом в кристаллографии).

Вывод групп симметрии впервые был осуществлен в 1826 г. немец-

ким кристаллографом М. Л. Франкенгеймом, затем независимо от него

в 1830 г. немецким минералогом И. Ф. Гесселем. Однако их работы были

не поняты и забыты современниками. И лишь в 1867 г. петербургский

академик А. В. Гадолин осуществил их строгий математический вывод и

показал, что существует всего 32 класса симметрии, полностью описыва-

ющие все возможные для кристаллов комбинации известных элементов

симметрии.

Зная основные правила взаимодействия элементов симметрии (пра-

вила умножения симметрических операций), нетрудно вывести все воз-

можные их сочетания.

Рассмотрев взаимодействия симметрических операций в общем виде,

увидим, что если оба элемента симметрии Iрода (связывающие конгру-

энтно равные фигуры — П с П или Л с Л), то асимметричная исходная

фигура дважды преобразуется в конгруэнтную ей и заменить эти две опе-

рации симметрии (т. е. совместить исходную фигуру с конечной) может

лишь операция

Ipoda

— простой поворот:

П-^П-^-»П.

При сочетании двух операций симметрии IIрода (связывающих зер-

кально равные

—

энантиоморфные

—

фигуры — П с Л) начальная П-фи-

гура под действием операции симметрии II рода преобразуется в энантио-

морфную (Л), а затем под действием второй (также операции II рода)

будет переведена в конгруэнтную исходной фигуру (П). Следовательно,

Кристаллография

кристаллохимия

заменить две проведенные операции

рода,

т. е.

связать конгруэнтные

—

исходную

результирующую — фигуры, сможет лишь операция симме-

трии Iрода

—

простой поворот:

П-И^Л-^-»П.

||>

Если

же

последовательно действуют операции разнородные

(I и II ро-

дов),

то

результирующей окажется операция IIрода, являющаяся резуль-

татом действия двух разнородных исходных симметрических операций

(движений):

п^п-^л.

iff '

Результирующим элементом симметрии

данном случае окажется

сложный элемент симметрии

рода

(см.

параграф

2.2.2),

задающий

две

симметрические операции, одной

из

которых будет операция

рода

—

по-

ворот,

второй — операция

рода — отражение

плоскости симметрии

либо инверсия

точке симметрии. Таким сложным элементом симметрии

будет либо зеркально-поворотная ось симметрии

—

если поворот

на

некото-

рый угол вокруг

оси

сопровождается отражением

плоскости симметрии,

перпендикулярной

оси

вращения, либо инверсионная

ось, —

когда поворот

сопровождается отражением

центре инверсии, находящемся

на

этой

оси.

Поскольку действие простых элементов симметрии можно заменить

действием соответствующих сложных: зеркальную плоскость

—

инверси-

онной осью

2-го

порядка

(Р = £.,),

центр инверсии — зеркально-поворот-

ной осью

2-го

порядка

(С = £

), то

симметрия любого многогранника

мо-

жет быть описана только

использованием осей симметрии

—

простых

(поворотных

LJ и (или)

сложных (зеркальных

или

инверсионных

2.6.1.

Осевая теорема Эйлера

Все

три

рассмотренных выше варианта взаимодействия элементов

симметрии составляют суть одной осевой теоремы Эйлера. Взаимодей-

ствие двух осей симметрии

п-го

порядка, поворотных

или

инверсионных,

приводит

возникновению проходящей через точку их пересечения третьей

оси симметрии.

При

этом результирующая

ось

окажется поворотной, если

исходными будут

две

одинаковые

оси (обе

поворотные

или обе

инверсион-

ные

), и

инверсионной, если исходные

оси

будут разного типа.

Эту теорему можно сформулировать

общем виде. Произведение двух

поворотов вокруг двух пересекающихся осей симметрии эквивалентно

по-

вороту вокруг третьей

оси,

проходящей через точку пересечения первых

двух,

т. е. два

вращения порождают третье, эквивалентное

им.

Глава 2. Симметрия кристаллов

Для доказательства нанесем на поверхность сферы выходы двух пе-

ресекающихся в ее центре поворотных осей (рис. 2.32) — А и В с эле-

ментарными углами поворота а и

соответственно. Результат сочетания

двух вращений вокруг указанных осей легко увидеть, рассмотрев движе-

ние точки на поверхности сферы (направления вращений указаны стрел-

ками).

Для этого на поверхности сферы проведем дуги больших кругов

(экваторы) а-а нЬ-b, полюсами которых служат выходы исходных осей

А и В соответственно. Рассмотрим последовательные вращения вокруг

указанных осей некоторой точки 1, выбрав ее на поверхности сферы так,

чтобы после поворота вокруг оси Л на угол а (движение по экватору а-а)

она оказалась на экваторе b-b в положении 2. После поворота точки 2 на

угол р вокруг оси В (движение по экватору b-b) она попадет в положе-

ние 3. Дуга большого круга, проведенная через точки 1 иЗ, является эква-

тором с-с по отношению к полюсу в точке С. При этом движение точки 1

по экватору с-с в точку 3 можно считать поворотом на угол у вокруг оси,

выходящей в полюсе С. Как видим, два поворота против часовой стрелки

вокруг пересекающихся осей А и В можно заменить поворотом в том же

направлении вокруг третьей оси

С:

{а)

•

2? = (7

(

. В этом суть известной

осевой теоремы Эйлера, лежащей в основе теории симметрии кристал-

лов.

Нетрудно понять, что комбинация вращений вокруг трех пересека-

ющихся осей соответствует операции идентичности, оставляющей точку

Рис.

2.32. К доказательству осевой теоремы Эйлера. Стрелками показано

перемещение точки по экваторам а-а, b-b, с-с при последовательном вращении

ее вокруг пересекающихся в центре сферы поворотных осей

симметрии А, В и С соответственно

Кристаллография и кристаллохимия

Эйлера с использованием половинных углов поворота рассматриваемых

осей симметрии, к которому можно прибегнуть для получения конкрет-

ных значений угловых величин.

Нанесем на поверхность сферы (рис. 2.33) выходы двух пересекаю-

щихся в ее центре О поворотных осей симметрии: точка А — выход оси

OA с элементарным углом поворота а и точка В — выход оси ОВ с элемен-

тарным углом поворота (3. Линия АВ — часть дуги большого круга, про-

веденного через выходы осей А

и 5

. Угол между этими осями соответ-

ствует отрезку АВ дуги большого круга, проходящей через их выходы.

Проведем на сфере дуги AM и AM', BNH BiY, образующие с дугой АВ

углы а/2 и (3/2 соответственно:

ZMAB

ZM'AB

= а/2, ZNBA = ZN'BA =

= (3/2.

Обозначим точки пересечения дуг AM с BN и AM' с BN

буквами С

и С соответственно. Рассмотрим движение точки С на сфере. В результате

поворота вокруг оси А на угол а против часовой стрелки точка С перейдет

в положение С. Последующий поворот точки С вокруг оси В на угол (3 в

том же направлении вернет ее в исходное положение С. Таким образом,

комбинация вращений вокруг осей А и В оставит точку С на месте. Это

значит, что третье — результирующее — вращение может происходить

исключительно вокруг оси, выход которой совпадает с точкой С, ибо

только в этом случае будет выполняться условие А

(а)

•

• С

(

= 1 и точ-

ка С при повороте вокруг третьей оси останется на месте. Величину угла

у легко измерить, рассмотрев полное перемещение точки А: поворот во-

круг оси А оставит точку на месте, поворот вокруг оси В переведет точку

Рис.

2.33. Построение Эйлера к доказательству осевой теоремы. ABC — сферический

треугольник, углы при вершинах которого соответствуют половинам элементарных

углов поворотов осей, выходящих в его вершинах. Стороны такого сферического

треугольника соответствуют углам между пересекающимися осями

Глава

Симметрия кристаллов

положение

А'. В

результате образуются

два

равных треугольника:

ААВС

АА'ВС,

ибо ZABC = ZA'BC = (3/2 и \JAB = иЛ'£ по

построению.

Следовательно,

ZACB

ZA'CB.

Обозначив каждый

из них

у/2, получим

элементарный угол поворота

у для оси С,

выходящей

точке

С.

Если взаимодействуют

две

инверсионные

оси, то

дважды повторен-

ная операция инверсии, содержащаяся

каждой

из

сложных осей, даст

операцию идентичности,

а два

вращения приведут

результирующему

вращению,

т. е.

появлению поворотной

оси

симметрии.

В результате проведенных построений получен сферический тре-

угольник

ABC,

углы

А, В и С при

вершинах которого равны половинам

элементарных углов поворота осей, выходящих

в его

вершинах,

т. е.

= а/2, В = (3/2 и С = у/2.

Стороны такого сферического треугольника

= \JBC, в =

и АС,

<иАВ соответствуют углам между этими осями.

Для решения сферического треугольника,

т. е.

определения

его

сто-

рон

а, Ь, с и

углов

А, В, С,

требуются знания основ сферической тригоно-

метрии,

без

которых невозможно решить многие задачи

не

только кри-

сталлографии,

но и

астрономии, геодезии

и т. д.

2.6.2.

Основы сферической тригонометрии

и ее

основные формулы

Сферическая тригонометрия

— это

раздел сферической геометрии,

в котором изучаются метрические свойства сферических треугольников

и методы

их

решения. Современный

вид

сферической тригонометрии

придали. Эйлер

(1707-1783) —

математик,физик,астроном. Швейцарец

по происхождению,

он с 1727 г.

работал

России,

а с 1741 г.

—

Берлине.

Он автор более

800

работ, оказавших значительное влияние

на

развитие

науки.

В сферической тригонометрии рассматриваются только такие фигу-

ры,

которые образованы дугами больших кругов,

т. е.

кругов, образован-

ных пересечением сферы

плоскостей, проходящих через

ее

центр. Часть

сферы между двумя полуокружностями

ее

больших кругов

(KJABDA^

и иАСЕАЛ, пересекающимися

по

линии

АА\

образует сферический дву-

угольник (рис.

2.34).

Угол между дугами

АВ и АС на

сфере равен углу между касатель-

ными

AM и AN,

проведенными

этим дугам

точке

их

пересечения

А,

и называется сферическим углом

CAB, а

точка

—

его

вершиной. Дуги

АВ

яАС~ стороны сферического угла.

Измеряется сферический угол

ВАС

лежащей

экваториальной пло-

скости дугой

DE,

заключенной между

его

сторонами.

Для

этой дуги вер-

шина угла

является полюсом,

т. е.

точкой пересечения сферы

перпен-

дикуляром, восстановленным

из ее

центра

плоскости большого круга

(экватору).

И под

словом дуга

этом случае понимается отрезок дуги

большого круга.

Кристаллография и кристаллохимия

Рис.

2.34. Сферический треугольник и его элементы

Длина дуги ВС пропорциональна величине центрального угла ф, т. е.

измеряется величиной угла ф между радиусами, опирающимися на ее

концы.

Часть сферы ABC, заключенная между тремя пересекающимися дуга-

ми окружностей ее больших кругов, называется сферическим треугольни-

ком (рис.

2.34).

В сферической тригонометрии рассматриваются только

те дуги, длина которых равна или меньше половины длины окружности.

Это ограничение носит название ограничения Эйлера.

Точки пересечения дуг, образующих сферический треугольник, назы-

ваются вершинами сферического треугольника и обозначаются буквами

А,

В и С. Противолежащие вершинам сферического треугольника дуги

называются сторонами сферического треугольника и обозначаются бук-

вами a, b и с. Таким образом, сферический треугольник ABC можно рас-

сматривать как часть сферы, ограниченную дугами а, Ь, с окружностей

ее больших кругов, полученных при пересечении сферы гранями трех-

гранного угла ОАВС, вершина О которого совпадает с центром сферы,

а грани содержат плоские дуги а, Ь, с, образующие стороны сферического

треугольника.

Сферические двугранные углы трехгранного угла ОАВС служат ме-

рой углов сферического треугольника ABC при его вершинах, а плоские

углы

ZBOC,

ZAOC,

ZAOB

того же трехгранного угла ОАВС являются

мерой его сторон а, Ь, с и измеряются в угловой мере — градусной или

радианной

1 радиан

—

это центральный угол, опирающийся на дугу, равную по длине

одному радиусу.

Глава

Симметрия кристаллов

Особенность сферического треугольника состоит в том, что сумма

всех углов больше 180°. В плоском треугольнике сумма всех углов равна

180°.

Однако поскольку каждый угол сферического треугольника мень-

ше 180°, то сумма его углов меньше 540° (< 3 х 180°). Таким образом,

180°<Л + В + С<540°.

Существуют разные способы решения сферического треугольника, т. е.

нахождения всех его элементов по нескольким заданным с помощью вы-

веденных формул, устанавливающих зависимость между элементами

сферического треугольника. Каждый сферический треугольник содер-

жит шесть элементов, и, чтобы его решить, нужно знать по крайней мере

три из них: либо три стороны, либо три угла, либо две стороны и угол и

т. д. Для того чтобы продемонстрировать использование законов сфери-

ческой тригонометрии при решении кристаллографических задач, сле-

дует знать ее основные формулы.

Теорема косинусов

Эта теорема, впервые доказанная Алъбатегнием в X в., устанавливает

зависимость между тремя сторонами (а,

Ь,

с) и одним из углов (А, В или С)

сферического треугольника.

Косинус стороны сферического треугольника равняется произведе-

нию косинусов двух других его сторон, сложенному с произведением сину-

сов тех же сторон па косинус угла между ними:

Докажем эту теорему.

Пусть ABC

—

сферический треугольник (рис.

2.35),

стороны Ьис ко-

торого меньше 90°. Соединив его вершины с центром сферы О, получим

центральные углы а', Ь' и с', пропорциональные величинам дуг, на ко-

торые они опираются, и численно равные сторонам сферического треу-

гольника: uCB = a, uAC

KJAB

= с.

Сферический угол (например, между дугами СА и АВ — угол CAB)

измеряется углом между касательными к этим дугам (AM и AN) в точ-

ке их пересечения (А). Пересечения этих касательных с продолжениями

радиусов ОВ и ОС дадут точки М и N. Из возникших плоских треуголь-

ников

AMNu

OMN по формуле косинусов находим

+ AN

- 2AM

•

cos A = OM + ON

- 20M

•

cos a,

20M- ON

•

cos a = OM + ON

- AM- AN

+ 2AM

-AN-cos

(2.6.1)

cos a = cos b

•

cos с + sin e

•

sin с

•

cos A.

AM + AN

- 2AM

•

cos A,

+ON

-20MON-

cos a,

откуда

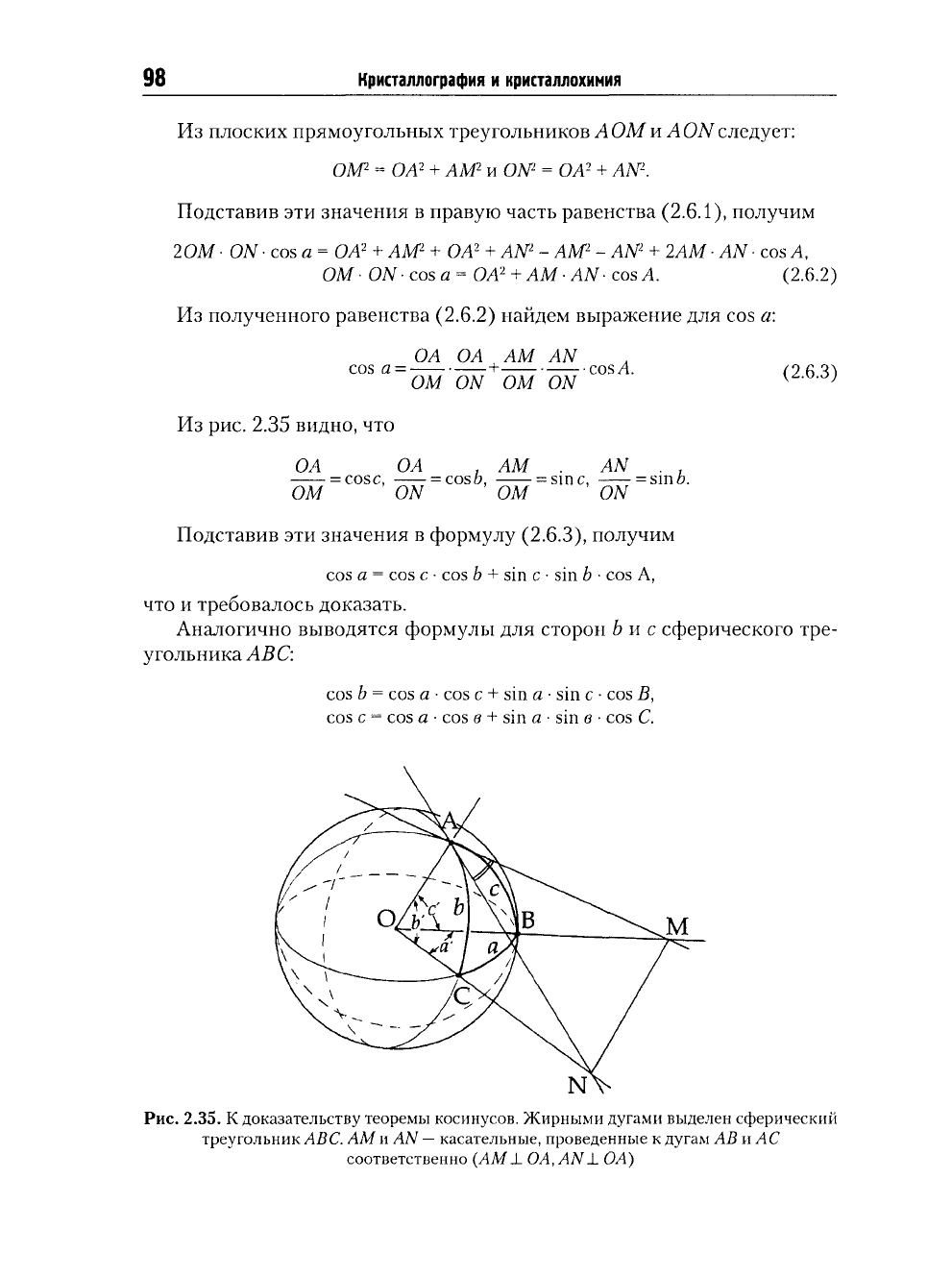
4 - 98.

Кристаллография

кристаллохимия

Из плоских прямоугольных треугольников

А ОМ и A ON

следует:

ОМ

- OA

+ AM

и ON

= OA

+ AN

Подставив

эти

значения

правую часть равенства

(2.6.1),

получим

2ОМ

•

cos а = OA

+ AM

+ OA

+ AN

- AM

- AN

+ 2AM AN cos A,

ОМ-ON-

cos a = OA

+ AM

•

AN• cos A. (2.6.2)

Из полученного равенства

(2.6.2)

найдем выражение

для cos а:

OA AM AN

cos a = + cos

А.

о к ч\

ОМ

ON ОМ ON

Из

рис. 2.35

видно,

что

OA , AM . AN . ,

-cose,

= coso, = sinc, = smo.

ON OM ON

Подставив

эти

значения

формулу

(2.6.3),

получим

cos а

cos с

•

cos

sin с

•

sin b

•

cos А,

что

требовалось доказать.

Аналогично выводятся формулы

для

сторон

b и с

сферического тре-

угольника

ABC:

cos b

cos a

•

cos с + sin a

•

sin с

•

cos B,

cos с = cos a

•

cos a + sin a

•

sin в

•

cos C.

Рис.

2.35. К

доказательству теоремы косинусов. Жирными дугами выделен сферический

треугольник

ABC. AM и AN

—

касательные, проведенные

дугам

АВ и АС

соответственно

(AM ±

OA,

OA)

Глава

Симметрия кристаллов

Следует оговорить,

что

выведенные формулы

для

сферических тре-

угольников

со

сторонами

Ьис,

меньшими 90°, могут быть использованы

для

треугольников

со

сторонами любой длины.

Из формул косинусов сторон сферического треугольника

(а,

Ъ,

с)

выводятся

все

необходимые

дальнейшем формулы сферической три-

гонометрии. Например, формулы косинусов углов сферического тре-

угольника

(А, В или С)

получаются

при

помощи введения полярного тре-

угольника,

т. е.

треугольника

А'В'С

(рис.

2.36),

вершины которого служат

полюсами сторон

(дуг)

исходного сферического треугольника

ABC.

Угол

данного сферического треугольника

ABC и

соответствующая

ему сторона

а'

полярного

с ним

треугольника Л'В'С

сумме составляют

180°,

т. е.

+ а = 180°.

Для доказательства этого положения обратимся

к рис. 2.36.

Продол-

жим стороны

АВ и АС

сферического треугольника

ABC до

пересечения

со стороной

В'С

полярного

с ним

треугольника

А'В'С в

точках

М и N.

Так

как

вершина

есть полюс дуги

В'С, то

дуга

служит мерой угла

А:

А = MN.

Дуга

В'С,

соответствующая стороне

а'

полярного треуголь-

ника, разбита точками

М и

на три

части,

то

есть

а' = В'М

NC.

Следовательно,

А + а'

В'М

MN+ MN+ NC =

B'N+MC.

А так как

точки

В' и С

служат полюсами дуг Л С

и АВ

соответственно,

то uB'N=

90°,

uMC

= 90°.

Следовательно,

А + а' = 90° + 90° =

180°,

что и

требовалось

доказать.

Таким образом,

а'= 180°,

//=180°,

(2.6.4)

+ с'= 180°.

Аналогично доказывается

положение

о том, что

сторона

(а)

дан-

ного сферического треугольника

соответствующий

ей

угол полярного

ним

треугольника

(А') в

сумме составляют 180°,

т. е.

+ А'= 180°,

+Я'=180°,

(2.6.5)

+ С - 180°.

Выведенные особенности взаимно полярных сферических треуголь-

ников позволяют распространить формулы

для

сторон сферического

треугольника

соответствующими изменениями

на его

углы,

наобо-

рот. Например, взяв

за

основу формулу косинуса стороны сферического

треугольника

cos а' = cos b'

•

cos с' + sin V

•

sin с'

•

cos A'