Егоров-Тисменко Ю.К. Кристаллография и кристаллохимия

Подождите немного. Документ загружается.

110

Кристаллография

кристаллохимия

возникнуть лишь

случае, если углы между заданными осями симме-

трии

—

и L

(

. и Z

— равны

90°.

В итоге получим следующие значения углов:

•

для

треугольника

L"L

все

углы между осями окажутся равны-

ми

90° (рис.

2.42а). Зафиксировав положения этих осей

на

сфере,

можно вычертить

стереографическую проекцию полученного

осевого класса симметрии

—

3L,

L'.

L"L

где все оси 2-го

порядка

не будут эквивалентны друг другу;

•

для

треугольника

две

стороны между осями

—

будут

равны

90°, а

угол между осями

— L.

= 60° (рис. 2.426).

Вновь,

нанеся выходы осей

на

сферу

построив стереографическую про-

екцию, получим (после размножения элементов симметрии друг

другом) также осевой класс —

где все три оси 2-го

порядка

будут связаны поворотами

на 120°

вокруг

оси L

следовательно,

эквивалентны;

•

для

треугольника

получим следующие значения

его

сто-

рон:

две

стороны между осями

— L.

90°, сторона L'

= 45°.

Вычертив этот сферический треугольник

(рис.

2.42в)

построив

стереографическую проекцию, увидим,

что

получен класс симмет-

рии

одной осью

четырьмя побочными осями

разбива-

ющимися

на

два неэквивалентных между собой семейства

—

класс

= L

2L'

;

•

треугольнике

'Z*

две

стороны

. — L.

90°, сторона

-L' =

30°.

итоге вновь получаем осевой класс

—

(

. 6L.

3L" так-

же

двумя неэквивалентными семействами осей

2-го

порядка

(рис.

2.42г);

•

для

треугольника

сторона

—

70°ЗГ44"

и две

сторо-

ны

—

54°44'08". Расположив рассчитанный треугольник

на

сфере

размножив данные элементы симметрии, получим стерео-

графическую проекцию

(рис.

2.42Э)

еще

одной осевой группы

—

;

• расчет углов между осями треугольника

даст следующие

их значения: угол между осями

— Z

54°44'08", между осями

-L

= 45° и I

- Z

35°15'32"

(т. е.

половина угла

в 70

31'44").

После размножения элементов симметрии друг другом

на

стерео-

графической проекции

(рис.

2.42е) снова получим осевую груп-

пу

- ЩЩ 6Z

В итоге получили шесть сферических треугольников

шесть соот-

ветствующих

им

осевых классов симметрии:

3Z,

3Z^4Z.

, первые четыре

из

которых характеризуются присутствием

лишь одного «единичного» направления

—

направления,

не

размножа-

ющегося другими симметрическими операциями класса симметрии.

Эти

Глава 2. Симметрия кристаллов

111

четыре класса в общем виде запишутся как L

•

. Следует обратить

внимание на то, что если порядок главной поворотной оси L

нечетный,

то все оси L

будут эквивалентны (например,

Ь^ЗЬ

Если же порядок

оси

—

четный, то оси L

, перпендикулярные главной, образуют две неэк-

вивалентные группы (например,

AL,

2L'

Две последние груп-

пы — 3L

— содержат несколько осей высшего порядка

и относятся к группам без единичных направлений.

Вывод остальных 26 классов симметрии удобно провести, убирая или

добавляя какие-либо симметрические операции (элементы симметрии)

к уже выведенным осевым классам.

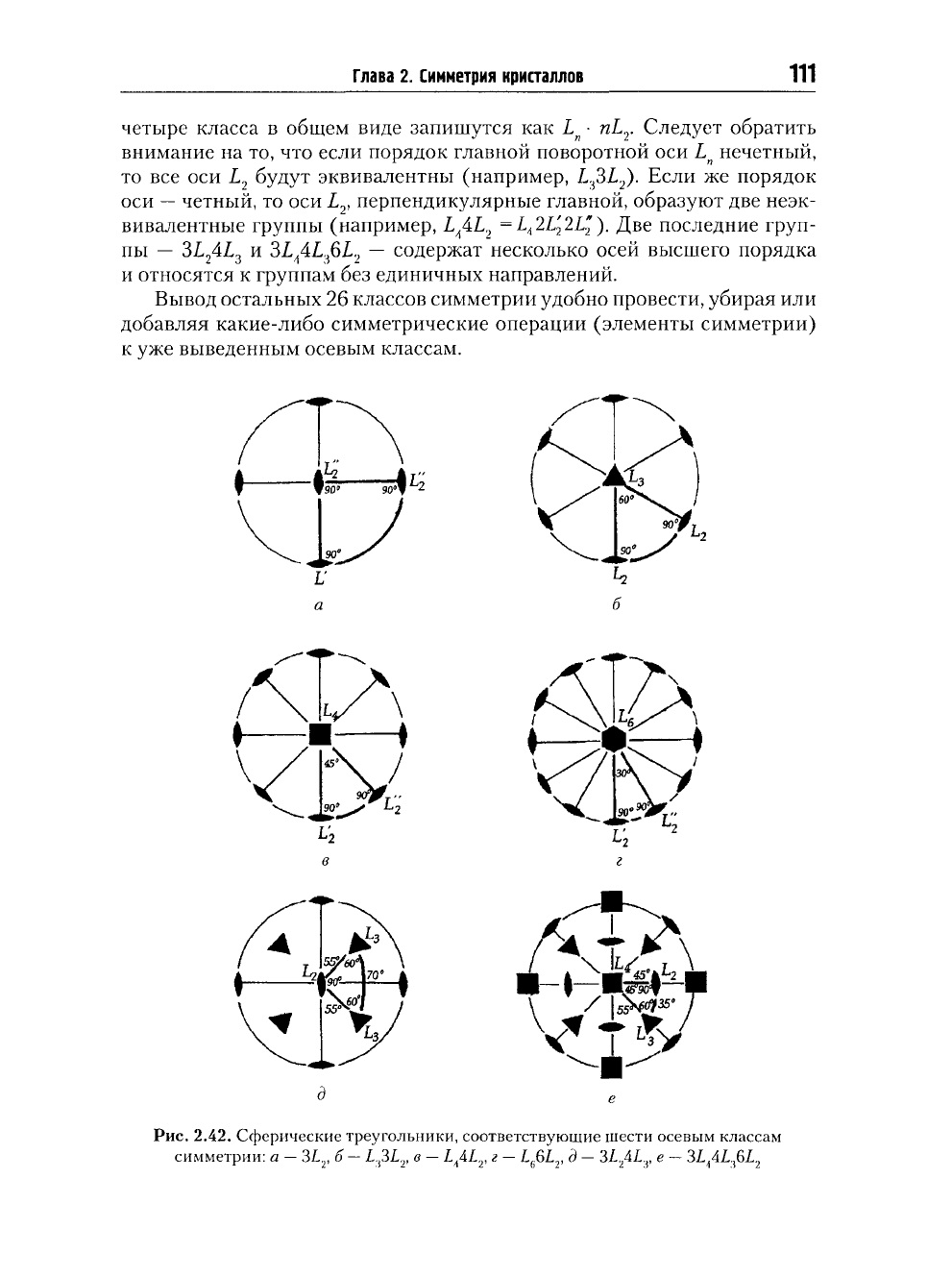
Рис.

2.42. Сферические треугольники, соответствующие шести осевым классам

симметрии:

а — 3L

, б

—

L^3L

—

АЬ

г —

.6L

д — 3L

е —

AL.fiL

112

Кристаллография и кристаллохимия

Вывод групп (классов) симметрии с единичными

особыми направлениями

Взяв за основу вывода полученные ранее четыре осевых класса L

- nL.,

и отбросив в них горизонтальные оси 2-го порядка (или все оси), по-

лучим пять новых циклических классов L

с единственной поворотной

осью,

среди которых появился класс 1

без каких-либо элементов симмет-

рии (кроме осей 1-го порядка):

, L

Остальные классы с единичным направлением — поворотной осью,

ориентированной вертикально в пространстве, можно получить добав-

лением к классу L\

1) вертикальной зеркальной плоскости симметрии (Р ), проходящей

вдоль каждой из осей Z

;

2) горизонтальной зеркальной плоскости симметрии (РД перпенди-

кулярной оси L

;

3) оси 2-го порядка, перпендикулярной оси L

;

4) операции инверсии в точке (г), т. е. центра симметрии, располо-

женного на оси L ;

5) любой комбинации перечисленных выше элементов симметрии.

Добавление указанных элементов симметрии к единственной оси и-го

порядка не нарушит единичности заданного направления (LJ в кристалле.

В результате (с у четом уже выведенных четырех осевых классов L

•

)

будет получено семейство из 27 классов симметрии с одним особым на-

правлением, не повторяющимся какими-либо симметрическими опера-

циями, т. е. с элементом симметрии, остающимся в группе симметрии

в единственном числе.

1. Добавление вертикальной зеркальной плоскости симметрии, рас-

положенной вдоль поворотной оси L

, приведет к возникновению групп

симметрии L

•

пР:

(Z,)P

= Р,

2P, L

3P,

L^AP,

6P.

Следует вновь обратить внимание на то, что если порядок поворот-

ной оси L

нечетный, то все плоскости будут эквивалентны между собой

(например,

ЗР).

Если же порядок осей четный, то плоскости, проходя-

щие через них, образуют две неэквивалентные группы (например, Ь

4Р =

= L.2P2F').

2. Добавление перпендикулярно расположенной к осям Ь

гори-

зонтальной зеркальной плоскости симметрии (Р

) приведет к классам

•

Р.:

п п

(L,)P

P,L

PC,L

P,L.PC,L

PC.

Глава

Симметрия кристаллов

113

В результате получим только четыре новых класса симметрии,

так

как добавление

Р к оси 1

приведет

к уже

выведенному ранее классу

Р =

LP = L Р

Классы

из

этого семейства

осями четного порядка

)

центро-

симметричны, поскольку

оси L , L

(

содержат поворот

на 180°.

Взаи-

модействие симметрической операции, задаваемой осью

L , с

операцией

отражения

перпендикулярной

Ь.

зеркальной плоскости

приводит

в соответствии

осевой теоремой Эйлера

(см.

параграф

2.6.1) к

резуль-

тирующей операции — инверсии

точке,

т. е. к

возникновению центра

симметрии

С (L,

= С).

3. Добавление центра инверсии

(С) к

единичному направлению, пред-

ставленному одной

из

поворотных осей четного порядка

приведет

к трем ранее выведенным классам симметрии

L PC =

PC,

L^PC,

LJPC,

так

как

взаимодействие четной

оси

симметрии, содержащей операцию

поворота

на

180°,

операцией инверсии

точке симметрии

(С)

приведет

к возникновению результирующей операции

—

отражению

зеркальной

плоскости симметрии, перпендикулярной исходной

оси

симметрии.

До-

бавление

же

центра инверсии

(С) к

поворотным осям нечетного порядка

(I,

L.,) изменит

их

характер,

т. е.

поворотные

оси

превратит

инверси-

онные.

итоге будут получены

два

новых класса

инверсионными ося-

ми:

+ С

+ C

Следует помнить,

что

каждая инверсионная

ось

имеет свой зеркаль-

но-поворотный эквивалент:

= £,

, £

= £

(

В предлагаемом выводе классов симметрии теряется одна

из

сложных

осей симметрии — инверсионная

ось £

(=£„),

так как эта

единственная

кристаллографическая

ось не

может быть получена никакими комбина-

циями иных элементов симметрии.

4. Добавление

единственной

оси

классов

или к

классам

•

со-

четания вышеперечисленных элементов симметрии приведет

классам

• nL„. • пР Р. или £,.. • nL.,

•

пР

При

этом если

каких-либо классах

21 v h

^1п 1 v L

перпендикулярно четной

оси L

(L,

, L

)

окажется зеркальная пло-

скость симметрии,

то

такие классы будут центросимметричны.

Следует обратить внимание

на

то,

что в

классах

•

nL,

горизонталь-

ными осями

2-го

порядка вертикальные плоскости симметрии

(Р

) от-

носительно осей

можно расположить двояко. Во-первых, совместить

иЬ.

—

этом случае обязательно возникнет горизонтальная плоскость

симметрии

(Р

)

(рис. 2.43а,б)

будут получены следующие классы:

3L,3PC

AL.pPC

=L^L,,

L&L1PC

= L.6L~6P

P. C,

ft 2 6 2_L г h '

но

3Z,,4P

= I., 3Z,„ 3P P..

1 3 2j_ г h

114

Кристаллография

кристаллохимия

б в г

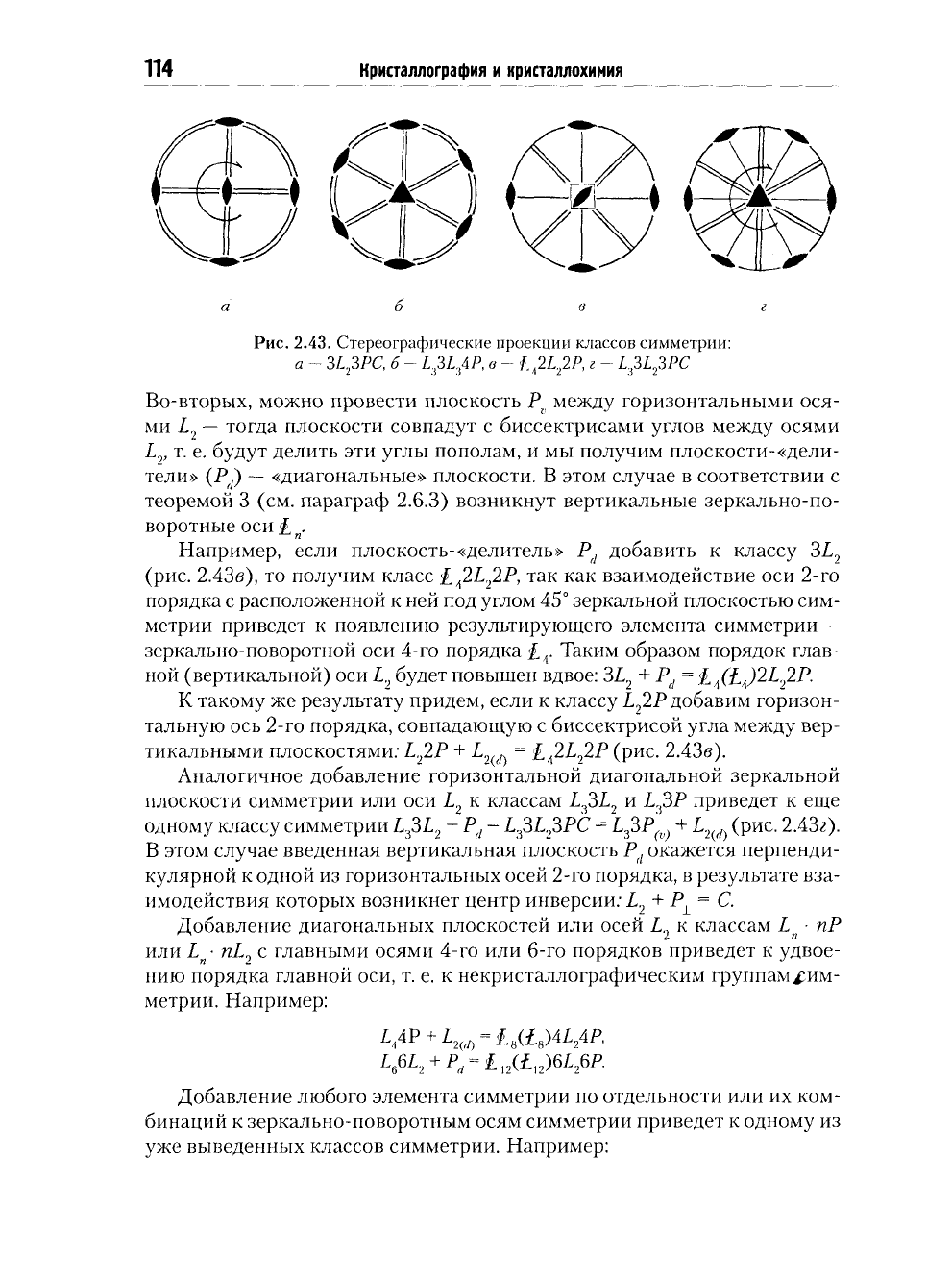
Рис.

2.43.

Стереографические проекции классов симметрии:

3PC,

б -

4P,

о -

f.,2L

2P,

г -

Ь.^ЗРС

Во-вторых, можно провести плоскость

между горизонтальными ося-

ми

— тогда плоскости совпадут

биссектрисами углов между осями

т. е.

будут делить

эти

углы пополам,

и мы

получим плоскости-«дели-

тели»

(Р

г/

)

— «диагональные» плоскости.

этом случае

соответствии

теоремой

3 (см.

параграф

2.6.3)

возникнут вертикальные зеркально-по-

воротные

оси £

Например, если плоскость-«делитель»

добавить

классу

ЗЬ

(рис.

2.43е),

то

получим класс £

2£

2Р,

так как

взаимодействие

оси 2-го

порядка

расположенной

ней под углом 45° зеркальной плоскостью сим-

метрии приведет

появлению результирующего элемента симметрии

—

зеркально-поворотной

оси 4-го

порядка

Таким образом порядок глав-

ной (вертикальной)

оси L

будет повышен вдвое:

3£

= £

(£

4У

)2£

2Р.

К такому

же

результату придем, если

классу £

2Р добавим горизон-

тальную

ось 2-го

порядка, совпадающую

биссектрисой угла между вер-

тикальными плоскостями: £

2Р

+ L

2(d)

2£

2Р (рис.

2.43e).

Аналогичное добавление горизонтальной диагональной зеркальной

плоскости симметрии

или оси L.

классам

и £.

;

ЗР

приведет

к еще

одному классу симметрии

L.^>L,

L.^>L.,3PC

(v)

2(d)

(рис. 2.43г).

В этом случае введенная вертикальная плоскость

окажется перпенди-

кулярной

одной

из

горизонтальных осей 2-го порядка,

результате вза-

имодействия которых возникнет центр инверсии:

+ Р = С.

Добавление диагональных плоскостей

или

осей

классам

•

пР

или

•

главными осями

4-го или 6-го

порядков приведет

удвое-

нию порядка главной

оси, т. е. к

некристаллографическим группам сим-

метрии. Например:

IH4P

Z.2(rf)

£8(£8)4L24P,

I66I2

+ Prf =

£12(£12)6I26P.

Добавление любого элемента симметрии

по

отдельности

или их

ком-

бинаций

зеркально-поворотным осям симметрии приведет

одному

из

уже выведенных классов симметрии. Например:

Глава 2. Симметрия кристаллов

115

It +

C-LfC,

+ P

=l,2L

2P,

В итоге получены 27 классов симметрии с одним единичным направ-

лением, представленным поворотной или зеркально-поворотной осью

симметрии.

Вывод классов симметрии без единичных направлений

Воспользуемся тем же способом, что и при выводе классов с единич-

ным особым направлением. Однако отбрасывание каких-либо элементов

симметрии в классах 3L

6L,

и 3LAL

выведенных с использованием

общей теоремы Эйлера (параграф

2.6.1),

приведет к уже полученным ра-

нее классам с единичным направлением. Поэтому остается лишь добав-

ление к указанным классам зеркальных плоскостей симметрии (Р) или

центра инверсии (С).

Добавление к каждому из указанных классов горизонтальной пло-

скости P

, являющейся координатной, (так как она перпендикулярна

вертикальной координатной оси Z), приведет в первом случае к самому

высокосимметричному классу

содержащему и координатные, и диагональные плоскости симметрии; во

втором случае — к классу

без диагональных плоскостей (рис. 2.44б). При этом оба класса окажутся

центросимметричными. Это значит, что добавление к исходным осевым

классам центра инверсии С привело бы к тому же результату.

3L^LfiL

+ P

= Ъ1

Мр1

ЪР^>Р

С (рис. 2.44а),

31,41,

+ Р.~ 3LAL.3P С

1 л h 2 Л к

9PC

3L4L ЗРС

2 3

3L4L6P

Рис.

2.44. К выводу групп симметрии кубической сингоний

116

Кристаллография

кристаллохимия

Добавление

классу 3£

4£

диагональной плоскости симметрии

—

плоскости, расположенной между горизонтальными осями

2-го

поряд-

ка, — приведет

новому нецентросимметричному классу,

котором

ко-

ординатные

оси Ь

повысятся

до

зеркально-поворотных осей

(= £ ).

Координатные

же

плоскости

этом случае будут отсутствовать:

= 3£

(рис.

2.44в).

В итоге выведены пять классов симметрии

несколькими осями выс-

шего порядка

—

классов

без

единичных направлений.

Вывод классов

без

единичных направлений

несколькими осями

высшего порядка можно осуществить

и не

прибегая

общей теореме

Эй-

лера, предполагающей знание основ сферической тригонометрии,

вос-

пользовались известными геометрическими данными: сочетания осей

высшего порядка могут быть такими,

как в

правильных многогранни-

ках — пяти Платоновых телах

—

кубе (гексаэдре), октаэдре, тетраэдре,

додекаэдре

(12

пятиугольных граней)

икосаэдре

(20

треугольных гра-

ней) (см. рис.

1.7).

Последние две фигуры некристаллографичны,

так как

содержат

оси 5-го

порядка. Поэтому обратимся

первым трем.

Общими элементами симметрии

для

всех трех многогранников

яв-

ляются четыре

оси 3-го

порядка (4£

), каждая

из

которых проходит:

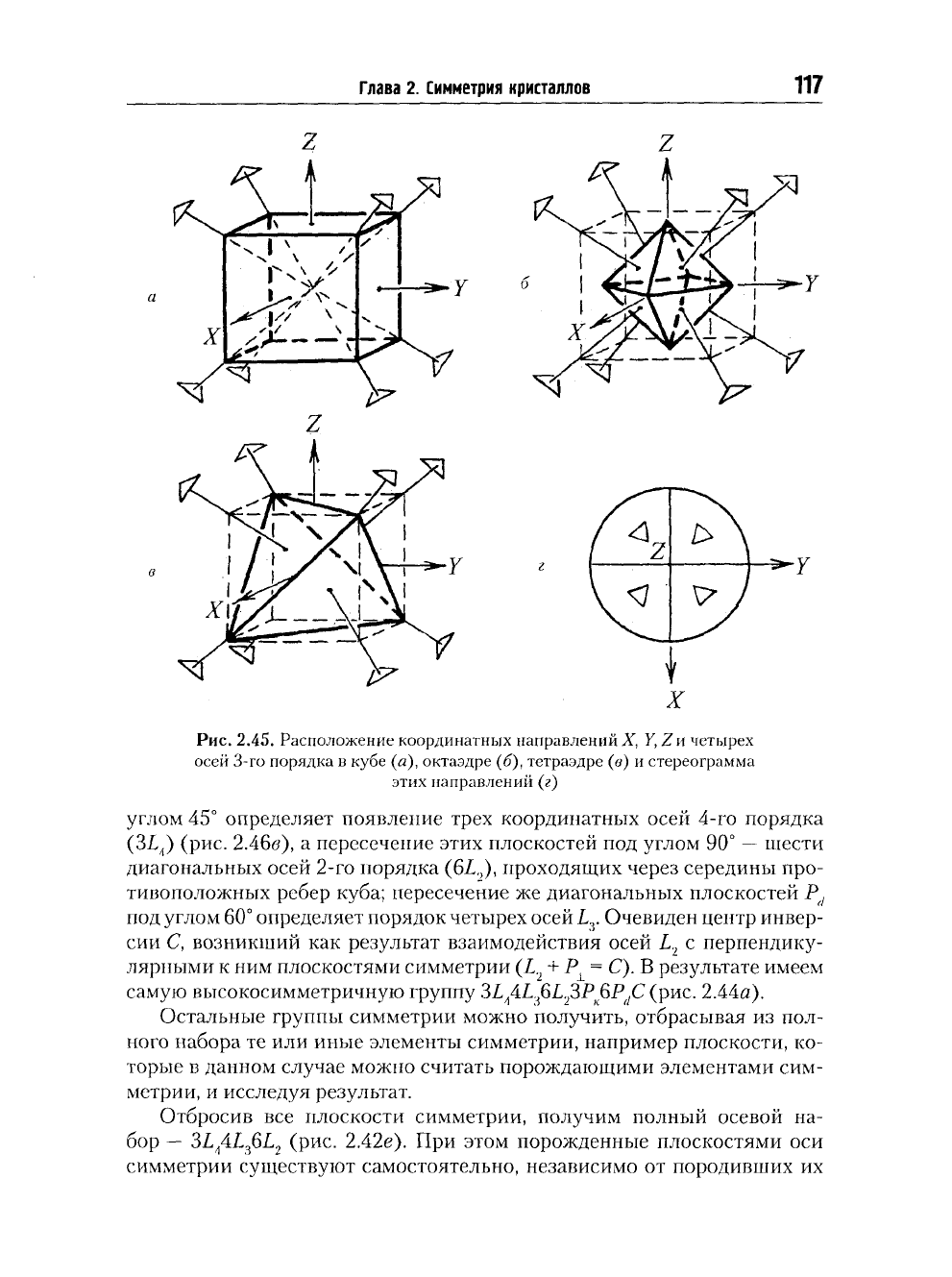
в кубе — через

две

противоположные вершины

(по

телесной диагонали

куба) (рис. 2.45а),

октаэдре

—

через середины противоположных граней

(рис.

2.456), в

тетраэдре

—

перпендикулярно каждой грани

(рис.

2.45в).

Расположение четырех осей

таково,

что

позволяет выделить

кри-

сталле

три

взаимно перпендикулярных эквивалентных направления,

которые можно принять

за

координатные. Эквивалентность указанных

направлений обеспечивается равнонаклонными

к ним

осями

3-го по-

рядка

(рис. 2.45).

Симметрия куба

октаэдра одинакова — число

рас-

положение вершин

граней куба соответствуют расположению граней

вершин октаэдра,

т. е. они

дуальны

(от лат. dualis

— двойственный) друг

другу. Причем симметрия куба

октаэдра заведомо выше,

чем

тетраэдра

(восемь треугольных граней

—

октаэдра

лишь четыре

—

тетраэдра).

Для получения всех групп симметрии

несколькими осями высшего

порядка удобно определить сначала полный набор элементов симметрии

куба

—

высшую (голоэдрическую) кристаллографическую группу симмет-

рии.

(От

греч. голёс (оА,ос;) — весь, полный, гедра (ебрсх)

—

грань.)

Очевидны

три

координатные плоскости симметрии —

ЗР

каждая

из

которых перпендикулярна одному

из

координатных направлений

X, Y

Z (рис.

2.46а),

шесть диагональных плоскостей симметрии

— 6Р

г1

проходящих вдоль осей

3-го

порядка

(т. е.

через каждую пару противо-

положных ребер куба)

(рис. 2.466).

Взаимное пересечение

и Р

г1

под

Глава 2. Симметрия кристаллов

117

Рис.

2.45. Расположение координатных направлений X, Y, Zu четырех

осей 3-го порядка в кубе (а), октаэдре (б), тетраэдре (в) и стереограмма

этих направлений (г)

углом 45° определяет появление трех координатных осей 4-го порядка

(31

) (рис. 2.46е), а пересечение этих плоскостей под углом 90° — шести

диагональных осей 2-го порядка

(61.,),

проходящих через середины про-

тивоположных ребер куба; пересечение же диагональных плоскостей P

под углом 60° определяет порядок четырех осей Ь.

Очевиден центр инвер-

сии С, возникший как результат взаимодействия осей L,

с перпендику-

лярными к ним плоскостями симметрии (L

+ Р = С). В результате имеем

самую высокосимметричную группу 3L

4L.fiL

3PJoP

C (рис. 2.44а).

Остальные группы симметрии можно получить, отбрасывая из пол-

ного набора те или иные элементы симметрии, например плоскости, ко-

торые в данном случае можно считать порождающими элементами сим-

метрии, и исследуя результат.

Отбросив все плоскости симметрии, получим полный осевой на-

бор — 3L

(

(рис. 2.42е). При этом порожденные плоскостями оси

симметрии существуют самостоятельно, независимо от породивших их

118

Кристаллография и нристаллохимия

плоскостей. Кроме того, существование осевой группы подтверждается

взаимодействием осей симметрии

—

и L

Удаление шести диагональных плоскостей понизит порядок коор-

динатных осей: ЗЬ

—> 3L

(взаимодействие координатных плоскостей

симметрии, пересекающихся под углом 90°, обусловит появление коор-

динатных осей 2-го порядка). В результате получаем группу 3L

4L.j5P

(рис.

2.446").

В группе, лишенной координатных плоскостей симметрии, обнару-

жим на координатных позициях только оси L

которые, однако, являются

лишь поворотными составляющими сложных осей 4-го порядка — L,

•

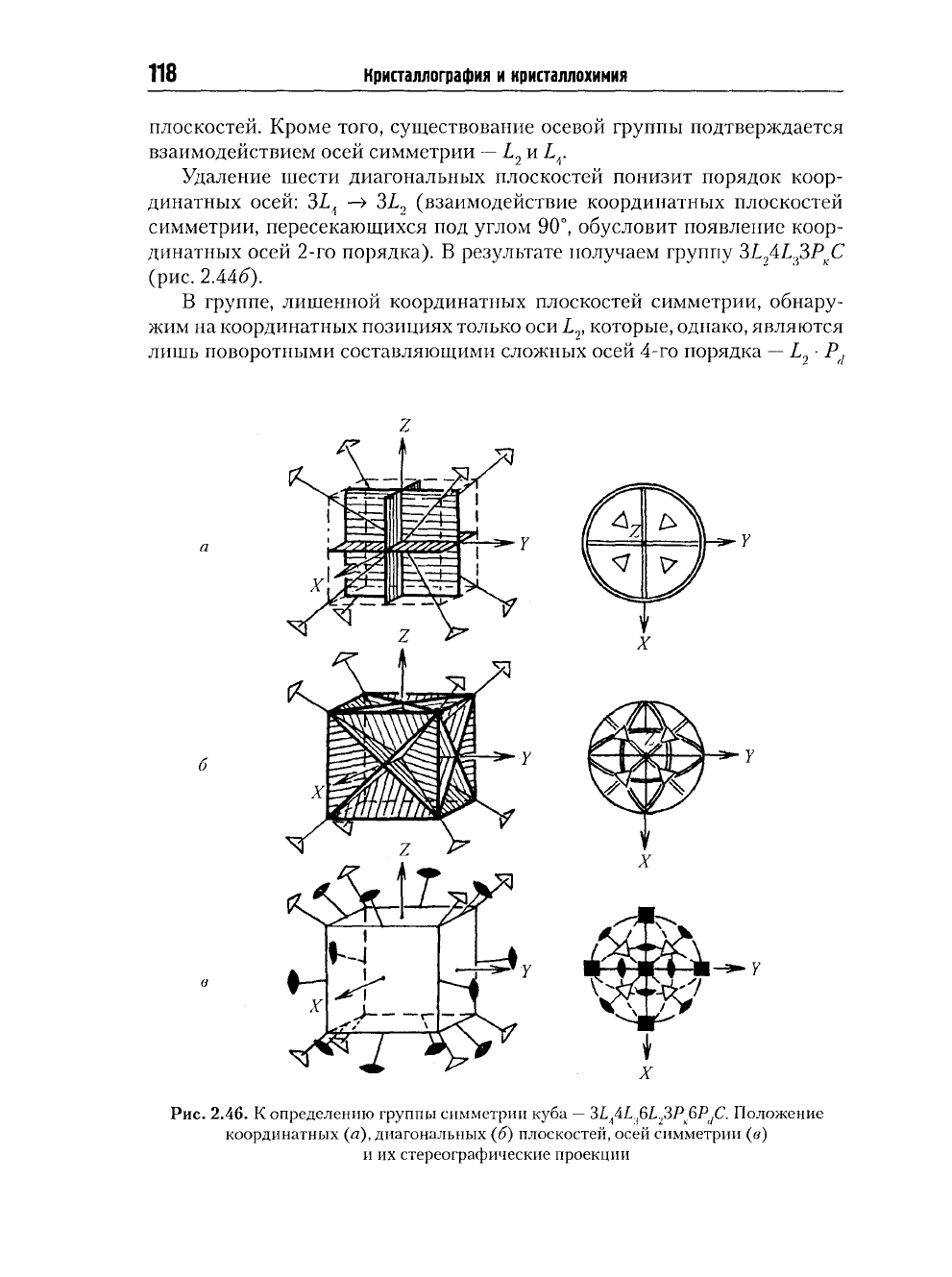
Рис.

2.46. К определению группы симметрии куба

—

4I,

;

,3P

Положение

координатных (я), диагональных (б) плоскостей, осей симметрии (в)

и их стереографические проекции

Глава 2. Симметрия кристаллов

119

(под углом 45°) = £

( = £

). Полученный класс 3£

42,

6Р

г/

—

класс симме-

трии тетраэдра (рис. 2.44в).

Наконец, оставив в последних двух классах только оси симметрии,

придем к самой младшей группе

—

ЗЬ

4Ь., (рис. 2.42Э). Причем, если для

группы 31

ЗР

С это очевидно, то для группы 3£

4Z,

необходимо

доказать невозможность существования «в чистом виде» осевого комп-

лекса 3£

42.

Действительно, если на координатном направлении оста-

вить ось £

, то это возвратит нас к исходной группе 3£

42,

6Р

г/

, так как

вертикальная ось

M(Z)

взаимодействуя с осью

2(X)

входящей в состав

оси ±.

А(Х)

, приведет к появлению уже отброшенных ранее шести диаго-

нальных плоскостей симметрии Р

г1

. Таким образом, вдоль координатных

направлений могут располагаться лишь 32,

— поворотные составля-

ющие осей £

В итоге и без использования теоремы Эйлера можно получить все те

же пять кристаллографических классов симметрии кубической сингоний.

2.7. ОБОЗНАЧЕНИЯ ГРУПП СИММЕТРИИ ПО А. ШЕНФЛИСУ

Кроме символики Браве, удобной в качестве учебной на первых эта-

пах изучения симметрии кристаллов, но достаточно громоздкой (по-

скольку в строчку выписываются все элементы симметрии данного клас-

са) и тем не менее не учитывающей всех операций симметрии группы,

широко используется символика, предложенная немецким математиком

А. Шенфлисом. Символика Шенфлиса позволяет одной буквой с соот-

ветствующим нижним индексом не только охарактеризовать весь набор

элементов симметрии конкретной точечной группы, но и объединить

родственные группы в отдельные семейства.

Переход от учебной символики Браве к символам Шенфлиса и обрат-

но предполагает знание правил взаимодействия элементов симметрии.

Циклические группы (L

) — группы с единственным особым направле-

нием, представленным поворотной осью симметрии,

—

Шенфлис предло-

жил обозначать буквой С с нижним цифровым индексом и, соответствую-

щим порядку этой оси (например, С

= L

, С

]

= 2.,). Следует иметь в виду,

что буквой С обозначается группа, а не элемент симметрии. Например,

— это класс с единственной осью 2-го порядка. Поэтому можно запи-

сать 32,

, но нельзя ЗС

, так как С

— это не ось, а класс симметрии.

Труппы с единственной инверсионной осью симметрии сопровожда-

ются нижним индексом i, например, С

з;

= £ , С. = £ . Если же инверси-

онной оси предпочитают ее зеркальный эквивалент, то группа с такими

осями обозначается S

(от нем.

spiegelaxe

— зеркальная ось), например

(

-(='l

)

= С

. (=£.,) , S

(=£

) = C

(=£

); при этом цифровой индекс

п всегда отвечает порядку сложной оси.