Егоров-Тисменко Ю.К. Кристаллография и кристаллохимия

Подождите немного. Документ загружается.

140

Кристаллография

кристаллохимия

в операции антисимметрии, «погасит» перемену знака (цвета); при этом

оставшиеся классические составляющие обусловят возникновение клас-

сического элемента симметрии

(см. рис. 2.626).

Поэтому «цветные»

операции симметрии — операции антисимметрии

— по

аналогии

опе-

рациями классической симметрии

2-го

рода

не

могут самостоятельно

составить группу симметрии. Взаимодействие разнородных операций

—

классической симметрии

антисимметрии (рис. 2.62б)

—

породит опера-

цию антисимметрии.

результате указанных взаимодействий возникнут

группы смешанной полярности — группы,

состав которых входят

как

классические операции, так

операции антисимметрии,

за

исключением

антиотождествления. Следует отметить, что антитождество, отсутствую-

щее

таких группах как, самостоятельная операция, входит

операции

антисимметрии, но уже

качестве их составной части.

Например,

на

рис.

2.606

изображена фигура смешанной полярности,

иллюстрирующая группу 4-го порядка,

—

4'. Эта группа включает четыре

следующие операции:

• антиповорот

на

90° —

(4')

• простой поворот

на

180° —

(4')

• антиповорот

на

270° —

(4')

(4')~

• отождествление — (4')"

= /.

При этом операция антитождества входит

состав сложных антипо-

воротов на 90° и 270°

качестве составляющей симметрических операций.

На рис. 2.60 хорошо видно, что порядок классической подгруппы

вдвое

меньше порядка исходной группы антисимметрии 4';

то

же справедливо

и для черно-белых групп 4-го порядка

т'т'2 и тт'2'

(рис.

2.626,

в), име-

ющих своими классическими подгруппами группы второго порядка

соответственно,

для группы 2-го порядка 1', содержащей

качестве

подгруппы классическую операцию тождества

(1)

1-го порядка.

Таким образом,

для

того чтобы получить группу антисимметрии

G',

нужно

классической подгруппе G добавить одну

из

удваивающих опе-

раций антисимметрии: 1', т!,

2', 1'. И

напротив, любую группу антисим-

метрии

известным порядком (числом

ее

членов) можно разложить

на

два равноправных независимых множителя так, чтобы один

из

них был

вдвое меньшего порядка, чем исходная группа, т.

е.

мог бы служить клас-

сической подгруппой,

второй — удваивающий множитель — возмож-

ной операцией антисимметрии.

Например, циклическая группа 6-го порядка —

6{6\ б

, б

, 6", б

, 6

}

(рис.

2.60) —

разлагается

прямое произведение двух сомножителей

(3-2)-

двух подгрупп: 3{

= 6

, 3'

, V

} и

2{1 =

, 2

= б

}. Первая

подгруппа (3-го порядка) может служить классической подгруппой,

вто-

рая (2-го порядка)

—

удваивающей группой антисимметрии:

•

6'.

Глава

Симметрия кристаллов

141

Группы

4-го

порядка

—

4 и 4

—

также разлагаются

на

два

члена

(4 =

2-2),

один

из

которых

(2)

является самостоятельной классической

подгруппой 2-го порядка, оставшийся

же

сомножитель

(2)

подгруппой

не

является,

вне

осей

4 и 4 не

существует

поэтому обозначается

4(mod2)

соответственно.

именно этот сомножитель группы может

служить удваивающей операцией

(но не

элементом симметрии!) групп

антисимметрии:

•

4' (mod2), 4'= 2

•

4'(mod2).

2.10.2.

Вывод точечных групп антисимметрии

групп смешанной

полярности

Вывод всех точечных групп антисимметрии,

как

было показано выше,

можно осуществить двумя путями: либо

точечным группам симме-

трии, принятым

за

классические подгруппы, добавить удваивающие

элементы антисимметрии, либо

каждой

из 32

точечных групп рассмо-

треть

все

возможные комбинации простых элементов

элементов анти-

симметрии.

В качестве примера рассмотрим вывод всех групп антисимметрии,

подчиненных (изоморфных,

см.

параграф

2.5)

точечным группам

ттт,

Зт,

23.

2 2 2

1. ттт =

— группа

8-го

порядка

тремя независимыми пло-

те

скостями симметрии

(т

•

т = 2

, т

независима) создает возможность

вывода групп антисимметрии двумя различными путями.

Во-первых, выписав подгруппы

4-го

порядка

(в два

раза меньшего,

чем порядок рассматриваемой группы):

222,

тт2 и

—,

добавляем

каж-

дой

из них

какой-либо удваивающий элемент антисимметрии:

1', т!

или

2'. При

этом количество групп антисимметрии будет соответство-

вать количеству выделенных классических подгрупп (рис.

2.63).

2' 2' 2

тт2

•

тт2

•

т'

тт2

•

тт2 -2' =

;

mmm';

mmm

2 2 2 2 2 2' 2'

—^•m =

—-т

—i--2=

—2--2

= ;—-

ттт;

ттт

, / ,2 2 2,,,

222-1'

222

•

т'

222 -т\'= 222

•

т'

=—

;

—;—-

—

т'т'т.

т т

Во-вторых,

тому

же

результату можно прийти, по-разному выделив

цветом порождающие элементы симметрии исходной точечной группы,

приняв

за

таковые

три

взаимно перпендикулярные плоскости симмет-

рии.

При

этом элементом антисимметрии может быть одна,

две или все

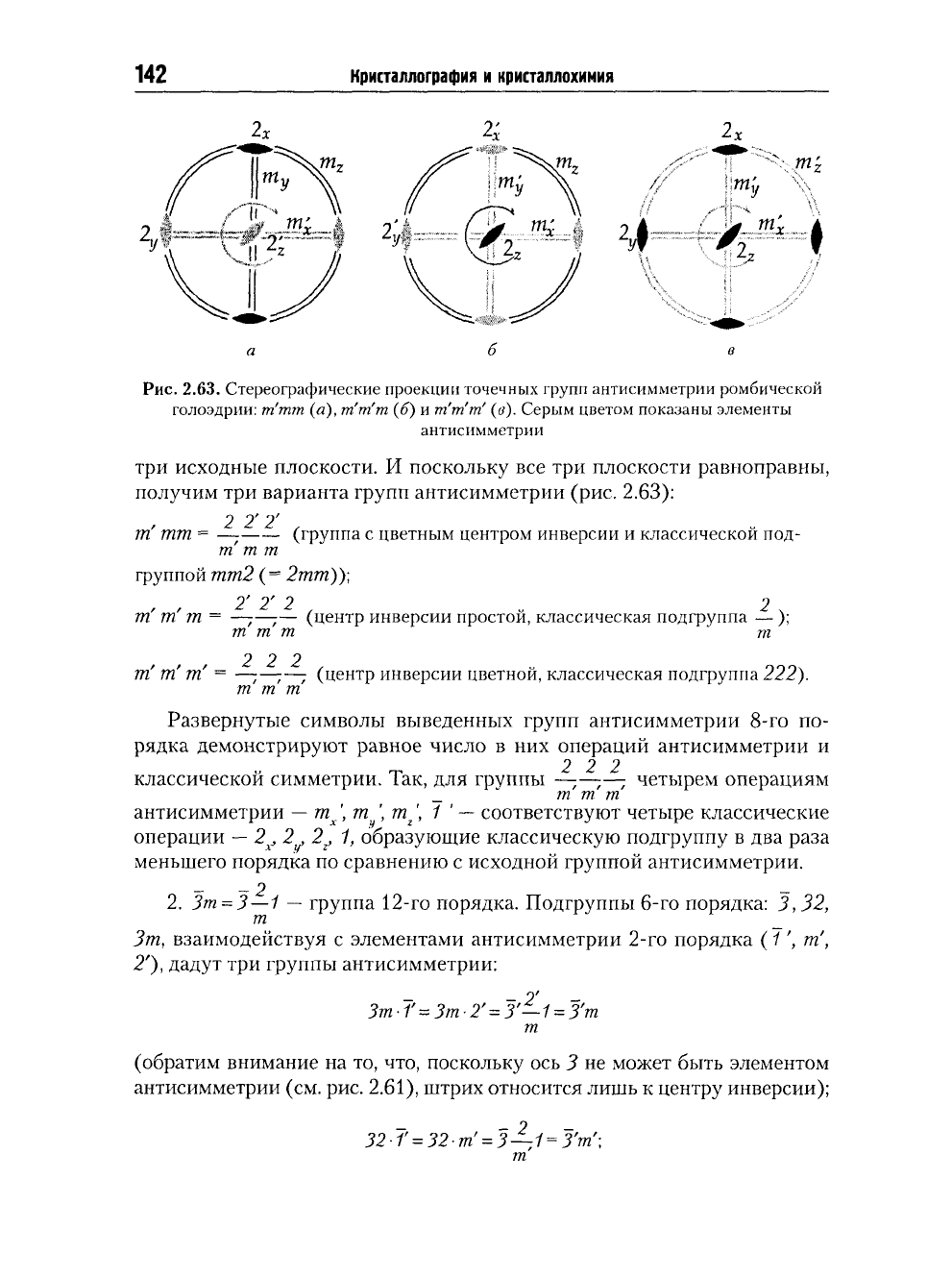
142

Кристаллография

кристаллохимия

т'у

пи

т;

Рис.

2.63.

Стереографические проекции точечных групп антисимметрии ромбической

голоэдрии:

т'тт (а), т'т'т (б) и

т'т'т'

(в).

Серым цветом показаны элементы

антисимметрии

три исходные плоскости.

поскольку

все три

плоскости равноправны,

получим

три

варианта групп антисимметрии (рис.

2.63):

2 2' 2'

т' mm = —

;

(группа

цветным центром инверсии

классической

под-

т т

группой

тт2 (= 2тт))\

2' 2' 2 2

т' т' т = —;—;—

(центр инверсии простой, классическая подгруппа

— );

т т т

2 2 2

т' т' т' =

—;—-—; (центр инверсии цветной, классическая подгруппа

222).

т т

Развернутые символы выведенных групп антисимметрии

8-го по-

рядка демонстрируют равное число

в них

операций антисимметрии

2 2 2

классической симметрии.

Так, для

группы —

;

—

;

—; четырем операциям

т т т

антисимметрии —

т^

\ т

', 1 '

—

соответствуют четыре классические

операции —

, 2

, 1,

образующие классическую подгруппу

в два

раза

меньшего порядка

по

сравнению

исходной группой антисимметрии.

- 2

Зт

3—1

— группа

12-го

порядка. Подгруппы

6-го

порядка:

3,32,

Зт,

взаимодействуя

элементами антисимметрии

2-го

порядка

(1', т',

2'),

дадут

три

группы антисимметрии:

Зт-1'

3т-2'

3'—1

3'т

(обратим внимание

на то, что,

поскольку

ось 3 не

может быть элементом

антисимметрии (см. рис.

2.61),

штрих относится лишь

центру инверсии);

32-1'

32т'

3~1

3'т;

Глава

Симметрия кристаллов

143

3-т'

3-2'=3—,1-Зт.

23 —

группа

12-го

порядка.

Не

имеет подгрупп порядка

поэтому

изоморфных

ей

групп антисимметрии

нет.

Кажущееся возможным

«за-

цвечивание» осей

2-го

порядка приведет лишь

серой группе

•

1'.

Итак, используя рассмотренные пути вывода шубниковских точеч-

ных групп симметрии, можно

на

основе

классических полярных

групп (введением операции антитождества

1')

получить

нейтральные

(серые) группы

и 58

групп смешанной полярности — собственно групп

антисимметрии,

т. е.

всего

122

группы (табл.

2.4), с

помощью которых

можно описать симметрию конечных фигур

объектов, обладающих

ка-

кими-либо прямо противоположными негеометрическими свойствами

(рис.

2.64). В

частности, группы антисимметрии используются

кристал-

лографической практике

при

выводе законов двойникования, описания

симметрии двойников

(см.

параграф

5.8.4),

электрических, магнитных

и других свойств кристаллов.

т'т'т 4'/тт'т'

6т'2'

6/т'т'т' т'З'т'

Рис.

2.64.

Иллюстрация некоторых точечных групп антисимметрии

144

Кристаллография

кристаллохимия

Таблица

2.4

Точечные группы антисимметрии

Классические Нейтральные Группы антисимметрии

Сингония

(полярные) (серые) смешанной полярности

Сингония

группы

G 1'

G =

G В(В= 1',

2',

т',

(mod2),

(mod2))

Триклинная

•

2 2- Г 2'

Моно-

т т-

т'

клинная

1-1'

2 2' 2'

т т т

т т'

222

•

2' 2'2

Ромбиче-

ская

тт2

2 2 2

тт2

•

III

. f

mm' 2', т' т'

2 2 2 2' 2' 2 2' 2' 2

ттт

т'т'т''

ттт'' т'т'т

3-1'

—

з-r

32 32- Г

32'

Зт Зт

•

Зт'

3~т Зт

•

З'т\

З'т, Зт'

6 6- V

•

Гексаго-

6 т2

6m2f

6'т'2,6т'

2', 6' т2'

нальная

622

•

6'22',

62'2'

1-f

6 6' 6'

1-f

m m

бтт

•

6' mm',

6m'm'

6 2 2

Lll

•

6 2 2 6 2' 2' 6' 2' 2

ттт

m m m m m mmm

6' 2 2' 6 2' 2'

mm'

m m

4 4- 1'

4-1'

Тетраго-

422

•

4 .,

42'

2',

4' 22'

4 4' 4'

нальная

—

•

m m

4тт 4тт

•

4m'm',

mm'

42т 42т

•

42'm',

4'2m, 4'2'm

Глава 2. Симметрия кристаллов

145

Сингония

Классические

(полярные)

группы G

Нейтральные

(серые)

группы G 1'

Группы антисимметрии

смешанной полярности

G' = G В(В= 1',2',т',

(mod2),

(mod2))

4 2 2

£11. f

4 2 2 4 2' 2' 4' 2 2'

ттт

т rn т ттт т т т

4' 2 2' 4 2' 2'

ттт ттт

Кубическая

432

-з

43т

±3*

т т

23 1'

432

•

2 -

—3 • Г

43т • 1'

• Г

т т

4'32'

2 -

о/

4'3т

4 -j 2 4' ^2' 4'-= 2'

—,3—,,

—,3 —, 3 ;

ттт ттт

Глава

СИМВОЛЫ ГРАНЕЙ

РЕБЕР КРИСТАЛЛОВ

3.1.

СИМВОЛЫ ГРАНЕЙ КРИСТАЛЛОВ. ЗАКОН РАЦИОНАЛЬНОСТИ ОТНОШЕНИЙ

ПАРАМЕТРОВ ГРАНЕЙ КРИСТАЛЛОВ

ЗАКОН ГАЮИ

Знание симметрии кристаллов, т.

е.

расположения элементов симмет-

рии

положения относительно этих элементов граней, фиксированных

сферическими координатами

ф и р

(см. параграф

2.3.1),

несмотря

на

про-

стоту

наглядность,

не

всегда позволяет понять

установить законо-

мерности взаимного расположения всех граней кристалла. Кроме того,

пользуясь лишь сферическими координатами, нельзя решить вопрос

реализации некоторой плоскости

качестве реальной грани кристалла.

Ответ

на эти

вопросы может дать индицирование — присвоение каждой

грани кристалла цифрового кристаллографического символа,

по

которо-

му даже

без

проекции можно разобраться

особенностях огранки того

или иного кристалла.

Для того чтобы такие символы получить, необходимо зафиксиро-

вать каждую грань кристалла

пространстве.

А для

этого необходимо

прежде выбрать

для

исследуемого кристалла кристаллографическую

координатную систему

(см.

параграф

2.4.3) и

затем измерить

те

отрезки

(параметры), которые грань кристалла, продолженная

до

пересечения

координатными осями,

на них

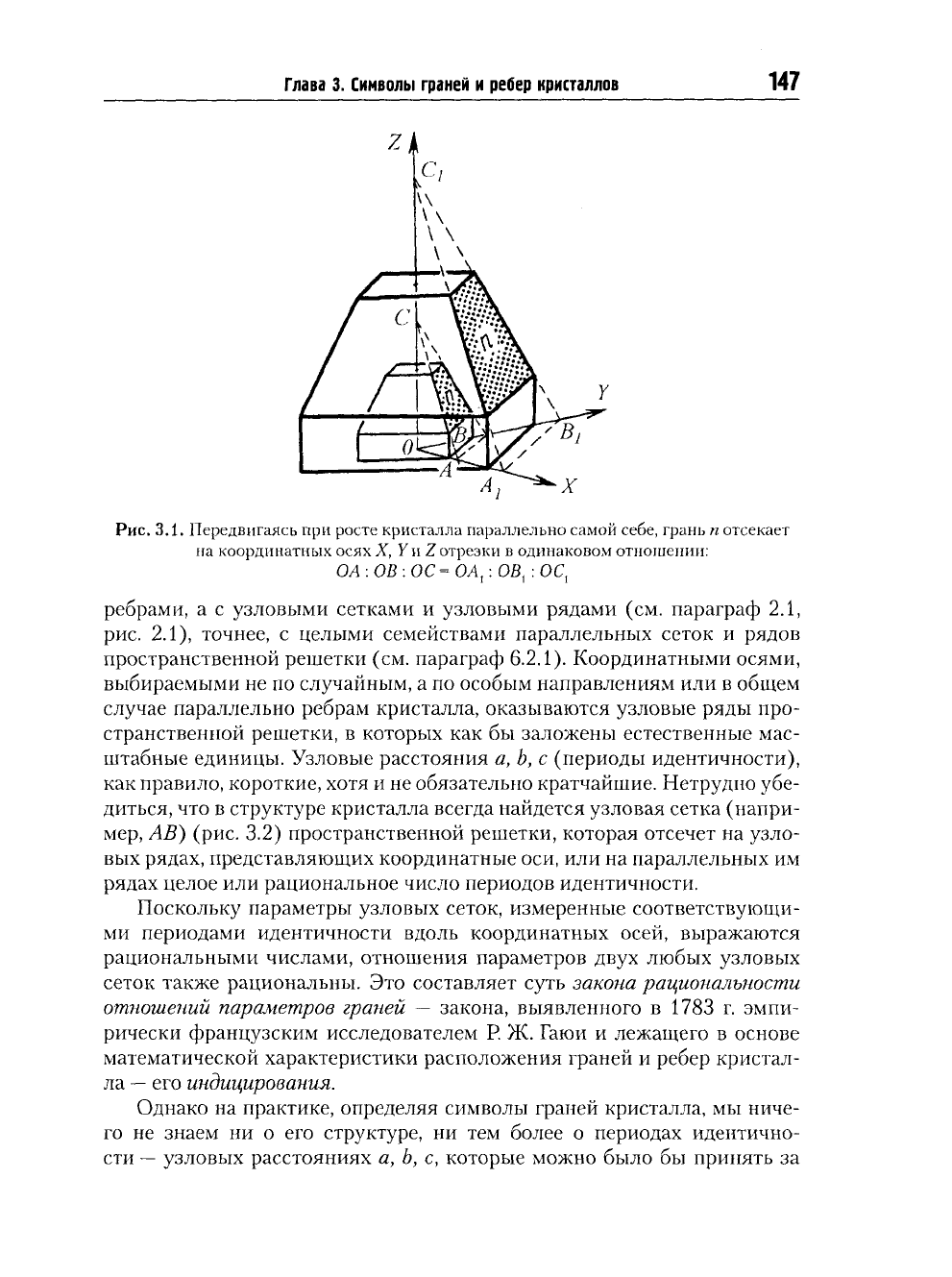
отсечет (рис.

3.1).

Таким образом положе-

ние грани будет зафиксировано.

Однако

при

росте кристалла параметры, отсекаемые каждой гра-

нью

на

осях

X, Г и Z,

будут меняться. Поэтому абсолютные величины

параметров грани

—

отрезки

OA, ОВ и ОС —

непостоянная

ее

харак-

теристика.

Но,

поскольку

при

росте грани кристалла перемещаются

параллельно самим себе, неизменными остаются отношения этих

от-

резков

(OA : ОВ : ОС = ОЛ

]

: О-В, : ОС

(

= const),

которые

фиксируют

положение любой плоскости, параллельной данной грани

(ABC)

отно-

сительно выбранных координатных осей.

Таким образом,

для

того, чтобы зафиксировать положение грани,

необходимо получить отношения

ее

параметров, измеренных

опреде-

ленных масштабах. Масштабы

же

заложены

самом кристалле

— его

структуре. Действительно, работая

кристаллами,

мы

фактически имеем

дело

не с

материальными плоскостями — гранями

или

действительными

Глава 3. Символы граней и ребер кристаллов

147

£>

\ \

—\—"к

(

Рис.

3.1. Передвигаясь при росте кристалла параллельно самой себе, грань п отсекает

на координатных осях X, У и Z отрезки в одинаковом отношении:

ОА:ОВ:ОС=ОА

:ОВ

: ОС,

ребрами, а с узловыми сетками и узловыми рядами (см. параграф 2.1,

рис.

2.1), точнее, с целыми семействами параллельных сеток и рядов

пространственной решетки (см. параграф

6.2.1).

Координатными осями,

выбираемыми не по случайным, а по особым направлениям или в общем

случае параллельно ребрам кристалла, оказываются узловые ряды про-

странственной решетки, в которых как бы заложены естественные мас-

штабные единицы. Узловые расстояния а, Ь, с (периоды идентичности),

как правило, короткие, хотя и не обязательно кратчайшие. Нетрудно убе-

диться, что в структуре кристалла всегда найдется узловая сетка (напри-

мер,

АВ) (рис. 3.2) пространственной решетки, которая отсечет на узло-

вых рядах, представляющих координатные оси, или на параллельных им

рядах целое или рациональное число периодов идентичности.

Поскольку параметры узловых сеток, измеренные соответствующи-

ми периодами идентичности вдоль координатных осей, выражаются

рациональными числами, отношения параметров двух любых узловых

сеток также рациональны. Это составляет суть закона рациональности

отношений параметров граней — закона, выявленного в 1783 г. эмпи-

рически французским исследователем Р. Ж. Гаюи и лежащего в основе

математической характеристики расположения граней и ребер кристал-

ла

—

его индицирования.

Однако на практике, определяя символы граней кристалла, мы ниче-

го не знаем ни о его структуре, ни тем более о периодах идентично-

сти

—

узловых расстояниях а, Ь, с, которые можно было бы принять за

148

Кристаллография и кристаллохимия

о о о о о о

Рис.

3.2. К доказательству рациональности отношений параметров

узловых сеток (граней)

единицы масштабов по соответствующим осям. Обратившись к рис.

3.3, на котором изображены две грани кристалла — плоскости ABC

и АВС

, увидим, что наиболее разумно в этом случае принять за еди-

ницы измерения (единицы масштабов) по каждой оси соответствую-

щие параметры некоторой грани этого кристалла (например, параме-

тры грани ABC, отношения которых OA : OB : ОС = а : b : с можно

г г

псе

е е е е е е

принять за отношения единиц масштабов по соответствующим осям).

Учитывая при этом то, что кристаллографические координатные оси

в общем случае неэквивалентны, единый масштаб измерения по всем

осям непригоден. В результате отрезки OA, OB и ОС, отсекаемые гра-

нью ABC (их отношение OA : OB : ОС = а : b : с), будут измерены мас-

штабами, предоставленными гранью АВС

, и положение искомой грани

ABC будет зафиксировано двойным отношением параметров граней

—

a b с a b с

—: —: —, при этом величины —: —: — для геометрических фигур могут

а„ К с, а, Ь

принимать любые значения, тогда как для кристаллов в кристаллографи-

ческой координатной системе они обязательно окажутся рациональны-

ми

а значит их отношение можно привести к отношению целых взаимно

.. a b с

простых чисел — индексов: р : а : г

—: —: —.

(

Эта особенность огранки кристаллов и была выявлена Р. Ж. Гаюи

и известна как важнейший закон, описывающий огранку кристалличе-

ских многогранников

—

закон Гаюи, закон целых чисел, или закон рацио-

нальности отношений параметров граней кристалла: двойные отноше-

ния параметров двух любых граней кристалла равны отношению целых

небольших взаимно простых чисел.

Обратим внимание на то, что а : b : с или а :Ь : с могут быть иррациональ-

ными.

Глава

Символы граней

ребер кристаллов

149

ОА

ОВ

:ОС

^а

:Ь

:с

Рис.

3.3. К

определению символа грани кристалла. Точками выделены единичные грани

В свете современных знаний этот закон представляет собой лишь

следствие особенности внутреннего строения кристаллов — трехмерной

периодичности

расположении материальных частиц: атомов, ионов,

молекул.

Индексы/;,

q,r—

индексы Вейсса

—

для

кристаллографической прак-

тики оказались неудачными,

так как для

граней, параллельных каким-

либо координатным осям, соответствующий индекс будет равен бес-

конечности

(оэ), что

неудобно

при

расчетах.

Это

побудило перейти

индексам

/г, k, I,

предложенным

в 1839 г.

профессором Кембриджского

университета

В.

Миллером

(1801-1880),

—

индексам Миллера:

, ,

1 1 1

е К

, 1

h :k ;/= —:-:- = — :~: —

где _ = 0 .

pgr а о с оо

Индексы Миллера

h, k, /,

заключенные

круглые скобки

(hkl) без

зна-

ков отношения (которые подразумеваются!), являются символом грани

кристалла.

, , ,

13 111

В нашем примере (рис. 3.3а)

q :г

: :

1 :3:

6;/?:&:/

—: —

6:2: 1, т. е. (hkl) = (621)

Очевидно,

что

символом грани, параметры

которой приняты

за

единицы масштабов

по

координатным осям,

т.

е.

грани,

задающей относительные масштабы

с,,

будет

(111),

отсюда

и ее на-

звание

—

единичная грань

. При этом надо помнить, что для индицирования

Читается «шесть—два—один»,

но не

«шестьсот двадцать один»!

Координатные

оси и

единичная грань задают

так

называемые геоме-

трические константы (элементы) кристалла: осевые углы

а, (3, у и а, : b : с =

—

:1:

— = а :\:с

К "