Егоров-Тисменко Ю.К. Кристаллография и кристаллохимия

Подождите немного. Документ загружается.

160

Кристаллография

кристаллохимия

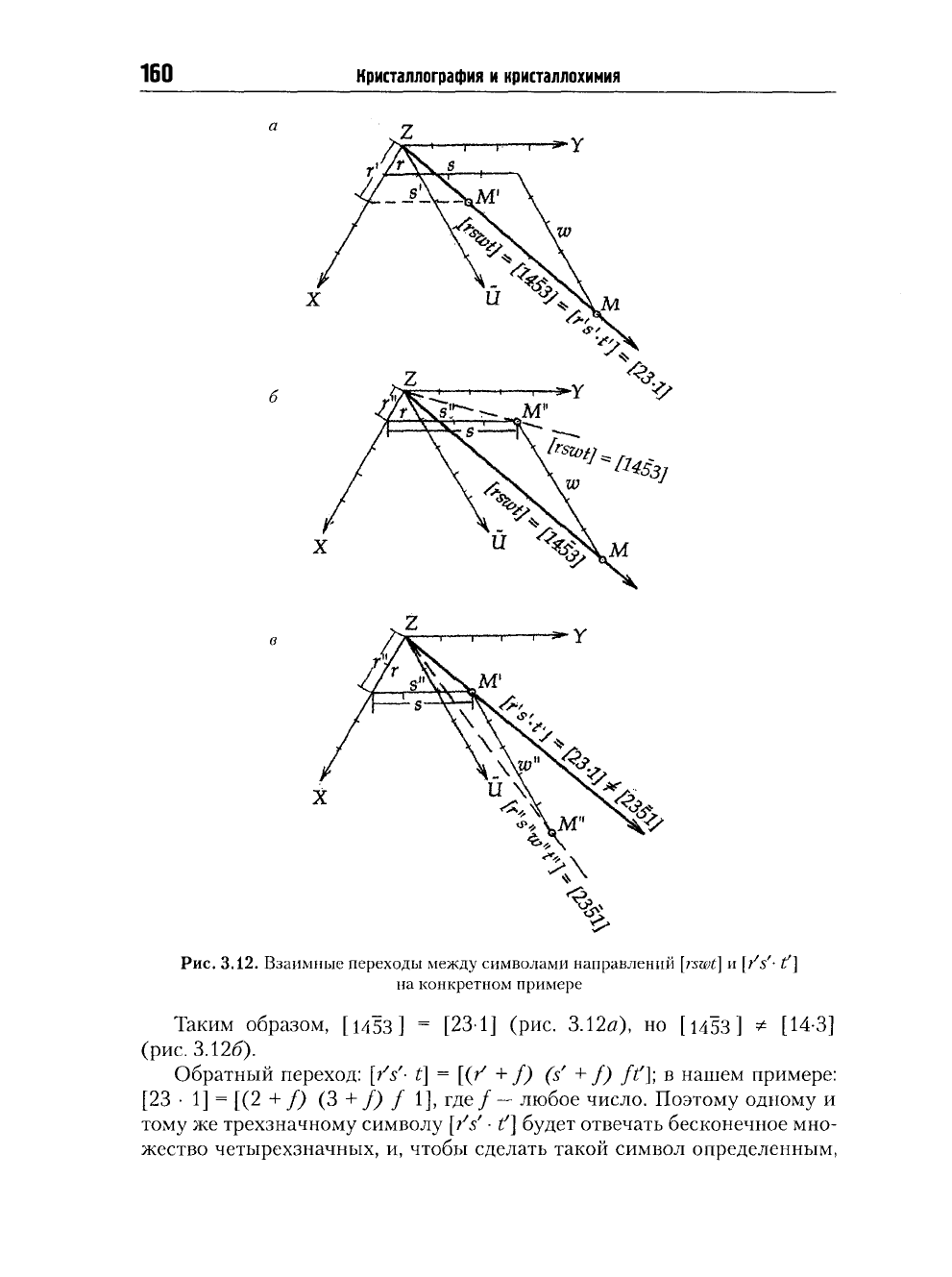
Рис.

3.12.

Взаимные переходы между символами направлений

[rswt] и \/s'- if]

на конкретном примере

Таким образом,

[1453 ]

[231] (рис.

3.12й),

но

[

1453 ] *

[

14-3]

(рис.

3.126).

Обратный переход:

[/s'- t] = [(/ + f) (s' + f) ff]; в

нашем примере:

[23 • 1] = [(2 + f) (3 + f) f 1],

где

/—

любое число. Поэтому одному

тому

же

трехзначному символу

[гУ

•

if]

будет отвечать бесконечное мно-

жество четырехзначных,

и,

чтобы сделать такой символ определенным,

Глава

Символы граней

ребер кристаллов

161

приходится вводить какое-либо дополнительное условие.

По

аналогии

с символами граней сумму первых трех индексов принято приравнивать

к нулю, хотя

данном случае геометрически

это и

неоправданно. Следо-

вательно,

приведенном выше примере

(2+У)

(3+/)+/=0и/=-5/3,

откуда

[(2-Ю (3-%) %

Л %

[1453].

Следует отметить,

что

отбрасывание знаменателя

(так же как со-

кращение индексов —

[69 • 3]

—>

[23 • 1])

приводит

тому,

что

индек-

сы символа ребра перестают быть координатами избранной точки

М,

поскольку

она

сместится вдоль ребра

позицию

М' на рис.

3.12а);

однако само ребро

при

этом

не

изменит своего направления.

Как

очевидно

из рис.

3.12в,

[23 • 1] * [2351 ]. Это

служит наглядным под-

тверждением тому,

что

правила, справедливые

для

символов граней,

нельзя механически переносить

на

символы ребер (координаты

то-

чек).

На

практике, например

для

получения символов ребер, связан-

ных какой-либо операцией симметрии (рис.

3.13),

можно вместо тра-

диционного четырехчленного символа пользоваться упрощенным,

где/=

0, т. е. [23 • 1] = [2301].

*~Y

Рис.

3.13.

Поворот ребра (точки) [

1453 ]

[2301]

вертикальной осью

3-го

порядка:

1. [2301] -> 2. [0231] -> 3. [3021] или [231] -> [ зТ

] -> [121 ]

3.3. ЗАКОН

ЗОН

(ПОЯСОВ)

ЗАКОН ВЕЙССА

Часто предпочитают говорить

не о

символе отдельного ребра,

а о

сим-

воле

оси

зоны

(или

просто

символе зоны)

(см.

параграф

2.3.4). А так

как зоной

или

поясом кристалла называют совокупность граней, пересека-

ющихся

по

параллельным ребрам,

то,

зная символы пересекающихся

- 98.

162

Кристаллография

кристаллохимия

граней, можно рассчитать символ ребра,

по

которому

они

пересекают-

ся,

т. е.

определить символ зоны.

Для

этого необходимо установить связь

между символами двух пересекающихся граней (плоскостей)

симво-

лом лежащего

плоскостях этих граней ребра (направления),

по

которо-

му

они

пересекаются.

3.3.1.

Связь между символами граней

ребер кристалла

Положение грани кристалла,

как

всякой плоскости, может быть опре-

делено уравнением общего вида:

Ах

+ Cz

где

х, у, z —

текущие координаты,

т. е.

координаты точки

на

плоскости;

А,

В, С —

коэффициенты;

D —

свободный член, прямо пропорциональ-

ный расстоянию плоскости

от

начала координат. Поскольку

кристал-

лах

это

расстояние

не

может быть зафиксировано,

то

свободный член

можно приравнять

нулю, рассмотрев уравнение плоскости, параллель-

ной данной

проходящей через начало координат:

Ах + By + Cz = 0. (3.3.1)

Известное

из

аналитической геометрии уравнение плоскости можно

записать

отрезках:

—+ —+ - = 1,

b с

где

а, Ь, с —

отрезки, отсекаемые плоскостью (гранью)

на

координат-

ных осях

X, Yn Z. И так же,

перенеся плоскость

начало координат,

по-

лучим:

—+ —+ - = 0,

a b с

111

или

л: +

_г

/ +

2 =

0. (3.3.2)

a b с

Сопоставляя уравнения

(3.3.1) и (3.3.2),

увидим,

что

отношения

об-

ратных параметров

— это не что

иное,

как

отношение коэффициентов

А,

В, С. С

другой стороны,

это

отношение соответствует отношению

ин-

дексов Миллера

h, k, / для

грани кристалла

при

условии,

что

параметры

грани

а,

Ь,

с и

текущие координаты

х, у, z

взяты

кристаллографической

координатной системе. Поэтому можно записать:

1 1 1

А:В:С=

---т--

=h:k:l.

a b с

Глава

Символы граней

ребер кристаллов

163

Таким образом, индексы Миллера

—

это

коэффициенты

при

текущих

координатах уравнения плоскости;

уравнение плоскости примет

вид:

hx + ky + lz = 0. (3.3.3)

Зная,

что для

кристалла индексы

h, k, I

всегда целочисленны, тогда

как

для

некоторой «случайной» плоскости

они

могут принимать любые,

даже иррациональные значения, можно сделать вывод

том,

что не

вся-

кая плоскость может реализоваться

виде грани кристалла,

лишь

та-

кая,

уравнении которой коэффициенты

при

текущих координатах, взя-

тых

кристаллографической координатной системе, рациональны,

т. е.

их отношение может быть сведено

отношению целых взаимно простых

чисел.

этом

состоит кристаллографическое «прочтение» уравнения

плоскости.

Какова

же

связь символа грани кристалла

(hkl) и

символа ребра

[rst],

лежащего

этой плоскости?

Поскольку символом ребра служат относительные координаты

лю-

бой

его

точки,

само ребро кристалла лежит

плоскости,

то

координаты

любой точки этого ребра должны удовлетворять уравнению данной пло-

скости.

этом случае текущие координаты

х, у, z в

уравнении плоскости

оказываются

не чем

иным,

как

индексами символа ребра, лежащего

в данной плоскости

(или

параллельного ей),

т. е. х: у: z = г: s: t. Из

опре-

деления символов грани

ребра следует,

что

их:

у:z

•

а :s

•

b :t- с ,

•J е ее

поэтому уравнение

(3.3.3) в

кристаллографической системе координат

примет

вид:

hr + ks + lt = 0. (3.3.4)

Это фундаментальное уравнение, выведенное Вейссом, связывает

символы грани

ребра кристалла, параллельного этой грани, или,

что то

же самое, символы грани

и оси

зоны, включающей

эту

грань.

Пользуясь уравнением

(3.3.4) и

зная символы двух граней

(/?,&,/,)

можно определить символ ребра

[rst], по

которому

они

пересе-

каются.

Для

этого нужно решить систему уравнений, составленных

для

каждой

из

пересекающихся плоскостей:

(3.3.5)

164

Кристаллография

кристаллохимия

Такие системы удобно решать способом перекрестного умножения:

\у

\ /

)

г:s:t

-к

1Л:(/г

/г,/

):(h

-h

Таким

же

образом можно вычислить

символ грани

(hkl), в

плоско-

сти которой лежат

два

пересекающихся ребра

[^s/J и [r

О,

hr.

Например, зная символы двух пересекающихся ребер куба,

т. е.

двух

координатных осей кристалла:

[100] — оси X и [001] — оси Z,

можно

рассчитать символ грани

(hkl), в

плоскости которой

они

располагаются

(рис.

3.14). Для

этого, составив систему уравнений:

А-1

+ *-0 +

/-0

0,1

/г-0

+ £-0

0,}'

и решив

ее

способом перекрестного умножения, определим символ

ис-

комой грани:

(nkl) = (0-0): (1-0): (0-0) = (010).

Итак,

две

грани определяют ребро

(ось

зоны),

два

ребра

(две

зоны)

—

грань кристалла. Отсюда ясно,

что

возможные грани

ребра кристалла

легко получить

по

четырем

известными символами граням,

три из ко-

торых

не

пересекаются

по

параллельным ребрам

(т. е. не

принадлежат

одной зоне),

или по

четырем ребрам,

три из

которых

не

лежат

одной

плоскости.

Это

положение отражает сущность закона Вейсса

(1804 г.),

или закона поясов (закона

зон):

всякая плоскость, параллельная двум

пересекающимся ребрам кристалла (принадлежащая двум

его

зонам),

представляет собой возможную грань кристалла,

всякое направление,

параллельное линии пересечения двух граней кристалла,

— его

возможное

ребро.

(3.3.6)

Глава

Символы граней

ребер кристаллов

165

Рис.

3.14. К

определению символа грани

по

символам двух пересекающихся ребер куба

3.3.2.

Графический метод определения символов граней

ребер кристаллов

Графический метод индицирования кристалла позволяет

не

толь-

ко рассчитывать символы возможных граней

ребер кристаллов,

но и

определять

их

сферические координаты

ф и р.

Этот метод использует

как стереографическое проецирование,

где

плоскость изображается

дугой большого круга,

направление — точкой

(см.

параграф

2.3.2), так

и гномостереографическое,

при

котором плоскость (грань) заменяется

нормалью

к ней и на

проекции изображается точкой,

соответственно

направление (ребро) заменяется перпендикулярной

нему плоскостью,

которая

на

проекции выглядит

как

дуга большого круга.

Например, найдем символ ребра

[rst],

по

которому пересекаются гра-

ни

(111)h(IJI)b

октаэдре.

Графически (рис. 3.15а) дуга большого круга, проходящая через гномо-

стереографические проекции граней

(111) и (iTl)

кубического кристал-

ла, проецирующихся

на

выходы осей

3-го

порядка, представляет собой

гномостереографическую проекцию ребра,

по

которому пересекаются

эти

грани. Полюс данной дуги, удаленный

от нее на

90°

(см.

параграф

2.3.4) и

имеющий

нашем случае координаты

ф =

270°

и р =

45°, является стерео-

графической проекцией данного ребра, совпадающего

одной

из

диаго-

нальных осей

2-го

порядка кубического кристалла

—

|Тш]

Расчет символа

[rst] искомого ребра подтверждает результат графического решения:

1 1 1

V"'

V \

X /

1 1 1

[«*]=(-

-1-1):(1-1):(1

+ 1)

[202]

[101],

или, что то же самое,

—

[101].

166

Кристаллография

кристаллохимия

Таким

же

образом можно рассчитать

символ плоскости

(hkl),

парал-

лельной двум пересекающимся осям

2-го

порядка

—

|Т|||

и 2

(

которая

окажется гранью октаэдра

символом

(111) и

проецируется

на

выход

оси

3-го

порядка —

, (рис. 3.156). При

этом дуга, проходящая через

выходы указанных осей

2-го

порядка,

не что

иное,

как

стереографическая

проекция искомой плоскости

(111).

Напомним,

что при

работе

кристал-

лами гексагональной сингоний

при

подобных расчетах традиционные

символы граней следует перевести

трехзначные

(см.

параграф

3.1.1).

Итак,

для

получения возможных граней

ребер кристалла графиче-

ским методом необходимо нанести

на

стереограмму

как

минимум четыре

грани

известными символами. Дуги больших кругов, каждая

из

кото-

рых проведена через любую пару граней, будут

не чем

иным,

как

гномо-

стереографическими проекциями ребер,

по

которым

эти

грани пересека-

ются. Символы этих ребер можно рассчитать

помощью приведенных

выше систем уравнений. Точки пересечения таких

дуг

укажут

на

пози-

ции возможных граней кристалла, символы которых также могут быть

рассчитаны.

Если необходимо определить символ какой-либо определенной грани

данного кристалла,

то,

нанеся

на

стереограмму

эту

грань

четыре грани

с известными символами, следует проводить дуги больших кругов

до тех

пор,

пока искомая грань

не

окажется

на

пересечении двух

дуг.

Метод графического получения возможных граней

ребер кристал-

ла называется методом развития

зон

(поясов)

или

методом Вейсса.

Однако

процессе развития

зон нет

необходимости каждый

раз

при-

бегать

промежуточному определению символов

зон

(ребер)

граней,

если воспользоваться некоторыми полезными следствиями

из

соотно-

шения

hr + ks + lt

1. В

символе любой параллельной координатной

оси

грани индекс,

соответствующий этой

оси,

равен нулю. Например,

символах граней,

[101]i\

i»>

— \

>"*•

•v.

\mi)

(111)//

Рис.

3.15. К

определению

кубическом кристалле симоволов

позиций:

а —

ребра,

по

которому пересекаются грани (111)и(1Ц);б

—

грани, параллельной осям

|7(|]|

и 2

|(Т|]

Глава

Символы граней

ребер кристаллов

167

параллельных

оси X, h = 0.

Действительно, символ

оси X

—

[100],

сле-

довательно,

•

1+&-0 + /0 = 0,

откуда

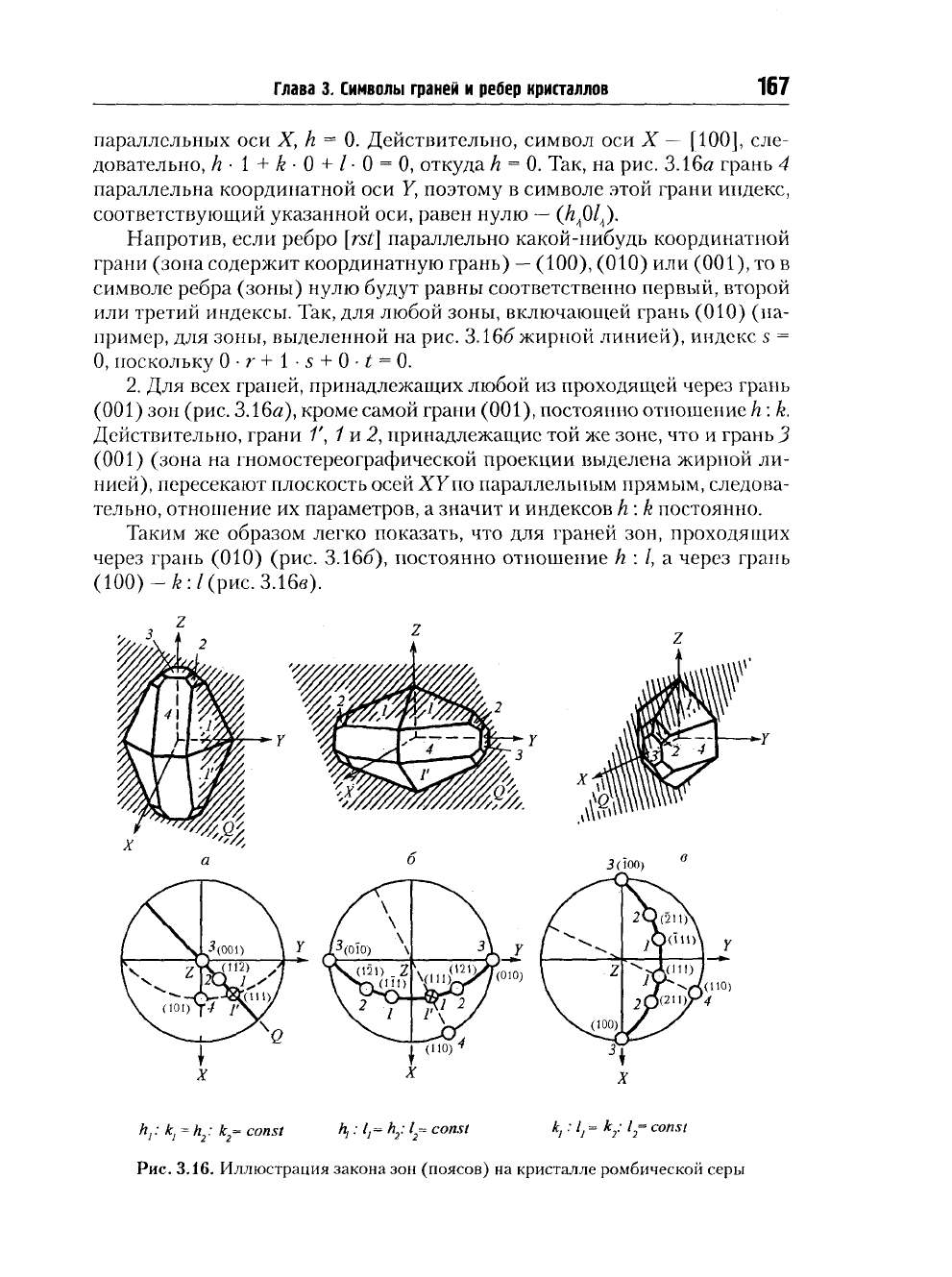
h = 0. Так, на

рис.

3.16а

грань

параллельна координатной

оси Y,

поэтому

символе этой грани индекс,

соответствующий указанной

оси,

равен нулю

—

Напротив, если ребро

[rst]

параллельно какой-нибудь координатной

грани (зона содержит координатную грань)

—

(100), (010) или (001), то в

символе ребра (зоны) нулю будут равны соответственно первый, второй

или третий индексы. Так,

для

любой зоны, включающей грань

(010) (па-

пример,

для

зоны, выделенной

на

рис.

3.166

жирной линией), индекс

s =

поскольку

0r+ls + 0- £ = 0.

Для

всех граней, принадлежащих любой

из

проходящей через грань

(001) зон

(рис. 3.16а), кроме самой грани

(001),

постоянно отношение

h: k.

Действительно, грани

1', 1 и 2,

принадлежащие

той же

зоне,

что и

грань

(001)

(зона

на

гномостереографической проекции выделена жирной

ли-

нией),

пересекают плоскость осей ХТпо параллельным прямым, следова-

тельно, отношение

их

параметров,

значит

индексов

h: k

постоянно.

Таким

же

образом легко показать,

что для

граней

зон,

проходящих

через грань

(010) (рис. 3.166),

постоянно отношение

h : /, а

через грань

(100)-А:/(рис.3.16в).

Рис.

3.16.

Иллюстрация закона

зон

(поясов)

на

кристалле ромбической серы

168

Кристаллография

кристаллохимия

Для

символов таутозональных

(см.

параграф

2.3.4)

граней

(hkl),

(h^kJ^),

)

и т.д., т. е.

граней, принадлежащих

одной зоне, суще-

ствует следующая зависимость: грань, символ которой получен простым

почленным сложением индексов двух других граней, принадлежит этой

же зоне. Конкретное положение этой грани

зоне укажут такие

две

гра-

ни

из

другой зоны, сложение символов которых даст

тот же

результат.

Действительно, если

две

грани

символами

(h^kj^)

)

пересе-

каются

по

ребру

символом

[rst],

то

что представляет собой уравнение плоскости

целочисленными коэф-

фициентами,

т. е.

грани, принадлежащей зоне

[rst].

Например, символ грани

(рис.

3.166)

можно получить, суммируя

символы граней

1 и 1': (111) + (ill) = (220) = (ПО)

(индекс

/ = 0

указывает

на то, что эта

грань параллельна координатной

оси Z с

симво-

лом

[001]).

Процедуру графического вывода возможных граней

ребер кристал-

ла методом развития

зон

можно существенно упростить, если взять

качестве исходных

не

любые случайные грани

известными символа-

ми,

а три

координатные

— (100), (010), (001) и

предварительно выбран-

ную единичную

— (111) и

использовать приведенные выше следствия

из

уравнения

ks + lt= 0.

Зоны рекомендуется проводить

следующей последовательности:

• через координатные грани

(рис.

3.17а)

—

получим зоны коорди-

натных осей;

• через единичную

координатные грани

(рис. 3.176) —

получим

двуединичные грани

(011), (101),

(НО)

;

• через двуединичные грани

(рис. 3.17в)

— получим грани

симво-

лами

(112) = (111) + (001), (121) = (111) + (010), (211) = (111) +

+ (100) и т. д.

Для

расчета символов двуединичных граней

и в

других случаях

при

таком

(последовательном) развитии

зон нет

необходимости прибегать

решению

си-

стем уравнений, достаточно воспользоваться приведенными выше следствиями.

Так,

из

следствия

очевиден символ грани

(ПО),

поскольку

она

параллельна

оси

(следовательно,

/ = 0) и

вместе

единичной гранью (111) принадлежит

проходящей через координатную грань (001) зоне (следствие

2), для

которой

постоянно отношение

k =

: 1.

Глава

Символы граней

ребер кристаллов

169

Во избежание ошибок

неоправданных усложнений рекоменду-

ется каждую последующую зону проводить через

две

грани

мини-

мальной суммой индексов. Например, проведя зону через

две

грани

известными простейшими символами

(001) и (121),

получим

три

новые

позиции

(I, II и III)

возможных граней кристалла

(рис.

3.17г).

Казалось

бы,

символ грани

получится суммированием индексов граней

(001) с

(121). И

действительно, символ

(122)

указывает

на то, что

грань

таким

символом должна принадлежать зоне

отношением

k = 1 : 2.

Однако

сумма индексов двух граней

(112) и (011)

другой зоны, которой также

принадлежит искомая грань

иная

— (123) — и не

подтверждает най-

денный символ. Сумма

же

символов граней

(111) и (011)

второй зоны,

пересекающейся

рассматриваемой, однозначно укажет

на

положение

грани

II с

найденным ранее символом

(122).

Тогда

символ грани

I —

(123)

— подтвердится равенством двух сумм индексов граней, принад-

лежащих разным зонам.

Символ грани

III — (120)

— очевиден: принадлежность

ее к

зоне

ко-

ординатной грани

(001)

определит отношение

h : k = const = 1:2, за-

данное символом грани

(121), а

расположение

ее в

вертикальном поясе

(поясе

оси Z)

однозначно укажет

на / = 0.

Таким

же

образом решается

обратная задача: зная позицию (коор-

динаты

ф и р)

некоторой грани, можно, последовательно развивая зоны,

прийти

к ее

символу.

Или,

наоборот, зная символ грани

(hkl),

можно опре-

делить

на

стереограмме

(по

четырем исходным граням)

ее

сферические

координаты

ф и р

(рис.

3.18). Эта

задача может быть решена, если прави-

ло сложения индексов, связывающее таутозональные грани, применить

в «противоположном» направлении,

т. е.

воспользоваться правилом рас-

щепления символов.

Например,

для

того чтобы определить сферические координаты гра-

ни

символом

(213) в

ромбическом кристалле,

где

положение единич-

ной грани фиксируется координатами

ф и р,

следует представить символ

этой грани

как

сумму символов различных

пар.

Расщепив символ

(213)

(001) (010) (001) (011) (010) (001) (011) (010) (001) (011) (010)

(100)

в г

Рис.

3.17.

Последовательность развития

зон при

определении

символов граней кристаллов