Егоров-Тисменко Ю.К. Кристаллография и кристаллохимия

Подождите немного. Документ загружается.

180

Кристаллография и кристаллохимия

а б в

Рис.

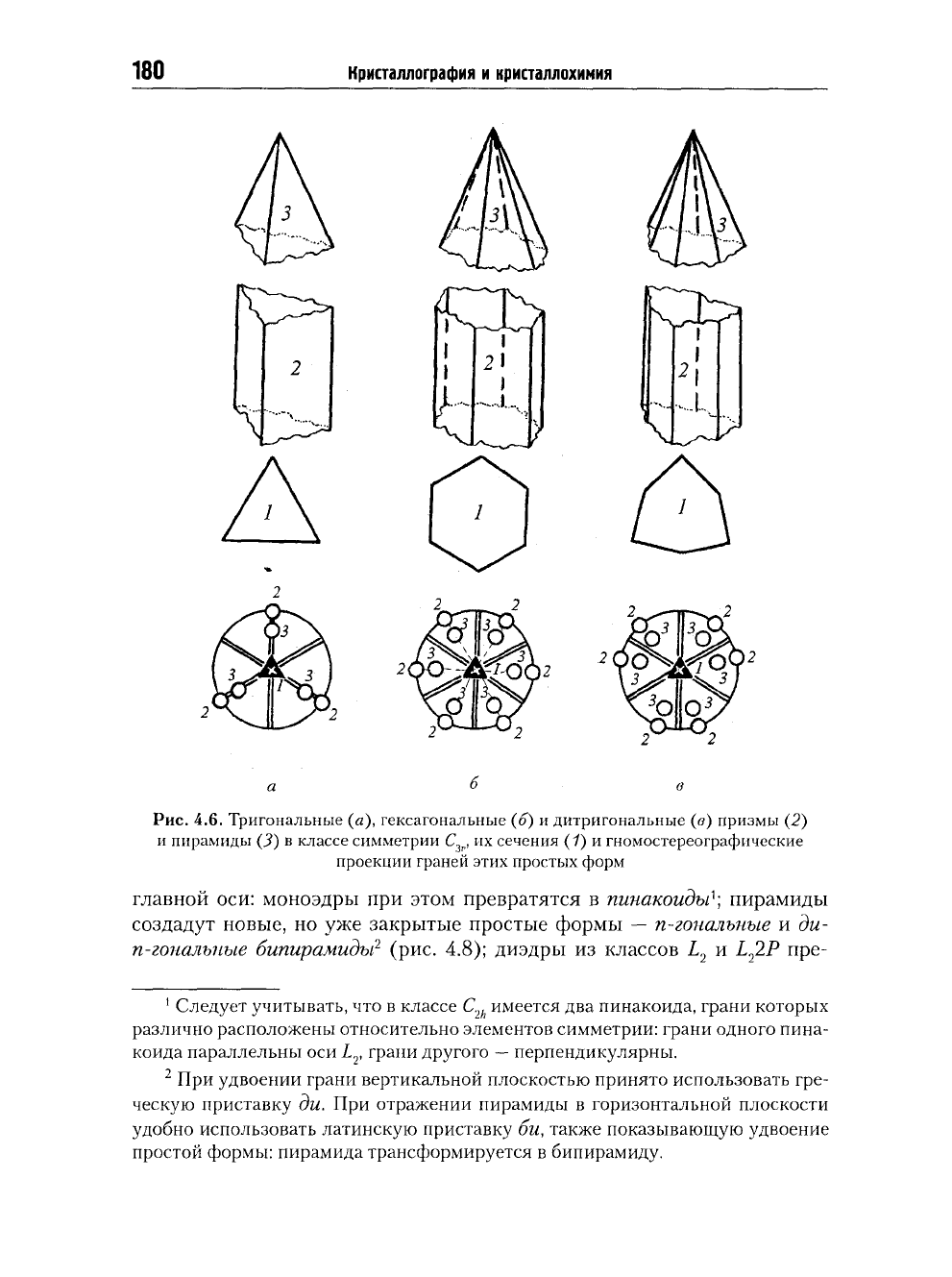
4.6. Тригональные (а), гексагональные (б) и дитригональные (б) призмы (2)

и пирамиды (3) в классе симметрии С , их сечения (1) и гномостереографические

проекции граней этих простых форм

главной оси: моноэдры при этом превратятся в пинакоиды

, пирамиды

создадут новые, но уже закрытые простые формы — п-гоналъные и ди-

п-гоиальиые бипирамиды

(рис. 4.8); диэдры из классов L

пре-

Следует учитывать, что в классе C.

имеется два пинакоида, грани которых

различно расположены относительно элементов симметрии: грани одного пина-

коида параллельны оси грани другого — перпендикулярны.

При удвоении грани вертикальной плоскостью принято использовать гре-

ческую приставку ди. При отражении пирамиды в горизонтальной плоскости

удобно использовать латинскую приставку би, также показывающую удвоение

простой формы: пирамида трансформируется в бипирамиду.

Глава 4. Простые формы кристаллов

181

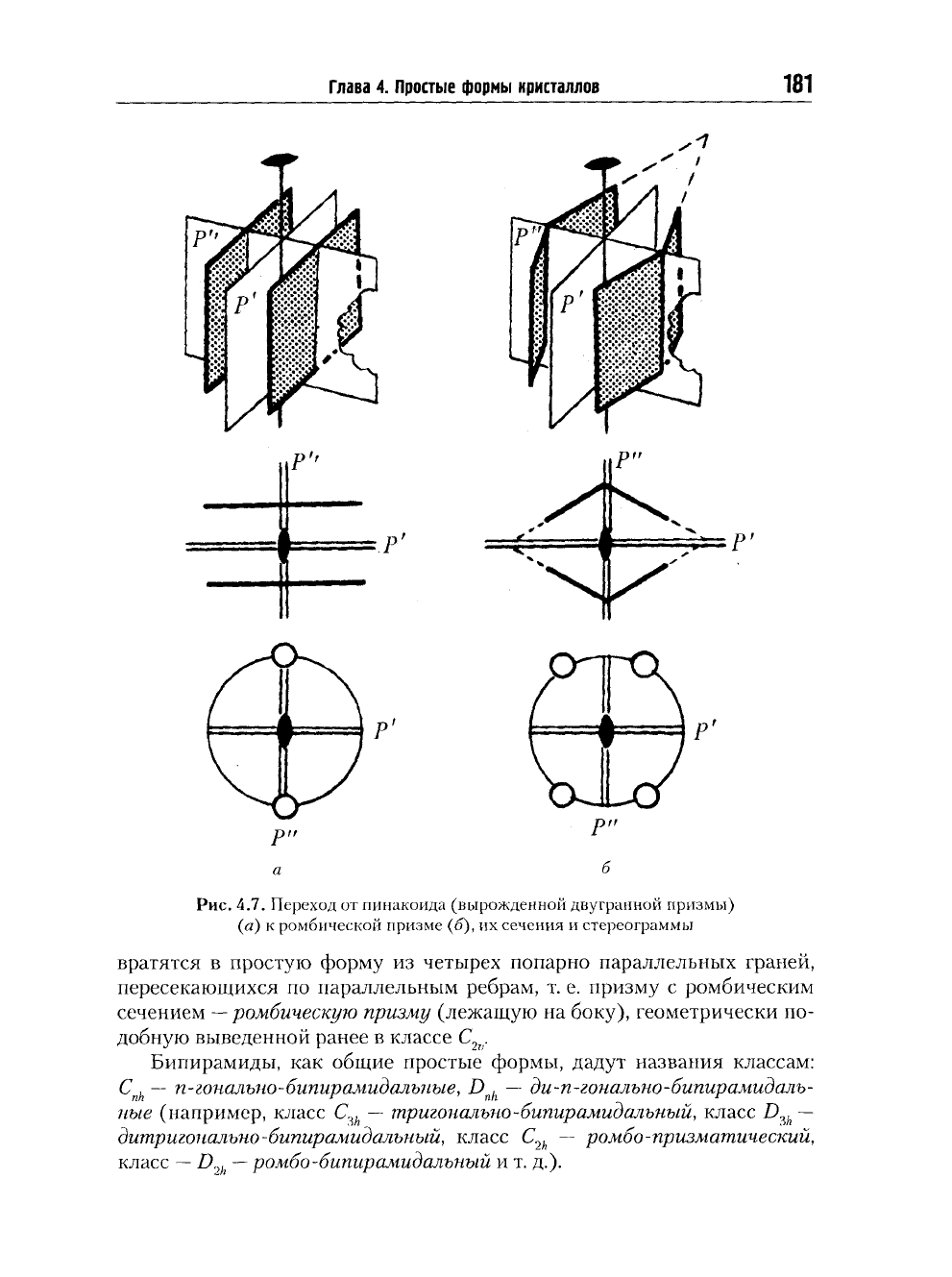
Рис.

4.7. Переход от пинакоида (вырожденной двугранной призмы)

(а) к ромбической призме (б), их сечения и стереограммы

вратятся в простую форму из четырех попарно параллельных граней,

пересекающихся по параллельным ребрам, т. е. призму с ромбическим

сечением

—

ромбическую призму (лежащую на боку), геометрически по-

добную выведенной ранее в классе С

2т

Бипирамиды, как общие простые формы, дадут названия классам:

— п-гоналъно-бипирамидалъные, D

— ди-п-гонально-бипирамидалъ-

пые (например, класс С.

— тригоналъно-бипирамидалъный, класс D

—

дитригоналъно-бипирамидальный, класс C

— ромбо-призматический,

класс

—

— ромбо-бипирамидальный и т. д.).

182

Кристаллография и кристаллохимия

а б о

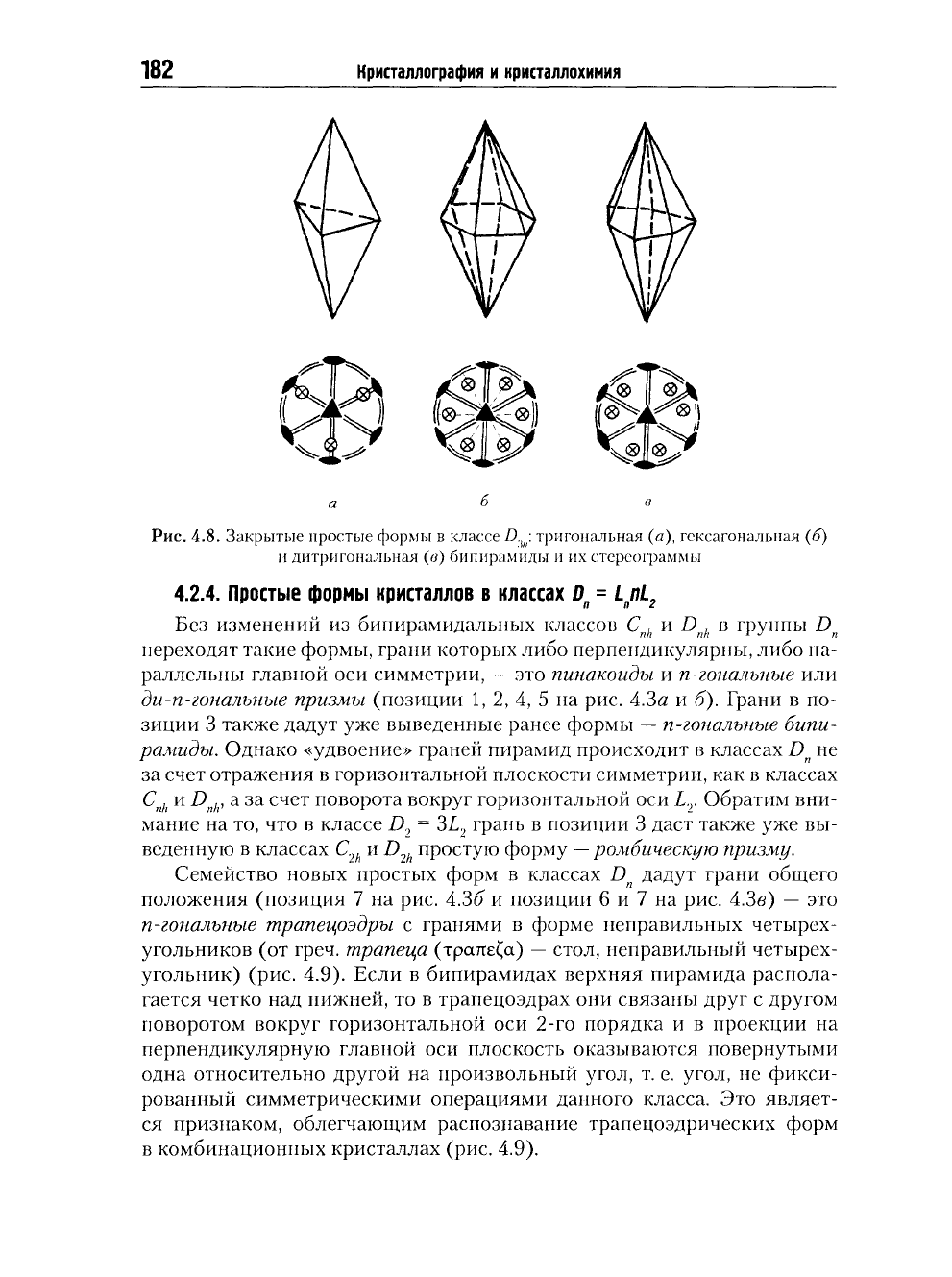
Рис.

4.8. Закрытые простые формы в классе D

тригональная (а), гексагональная (б)

и дитригональная (о) бипирамиды и их стереограммы

4.2.4.

Простые формы кристаллов в классах 0 =

LnL2

Без изменений из бинирамидальных классов C

и D

в группы D

переходят такие формы, грани которых либо перпендикулярны, либо па-

раллельны главной оси симметрии, — это пииакоиды и п-гоиальные или

ди-п-гоналъные призмы (позиции 1, 2, 4, 5 на рис. 4.3а и б). Грани в по-

зиции 3 также дадут уже выведенные ранее формы — п-гоиалъные бипи-

рамиды. Однако «удвоение» граней пирамид происходит в классах D

не

за счет отражения в горизонтальной плоскости симметрии, как в классах

и D

, а за счет поворота вокруг горизонтальной оси L.,. Обратим вни-

мание на то, что в классе = 3L.

грань в позиции 3 даст также уже вы-

веденную в классах С

и D.

простую форму

—

ромбическую призму.

Семейство новых простых форм в классах D

дадут грани общего

положения (позиция 7 на рис. 4.36 и позиции 6 и 7 на рис. 4.3в) — это

п-гональные трапецоэдры с гранями в форме неправильных четырех-

угольников (от греч. трапеца (трале(а) — стол, неправильный четырех-

угольник) (рис. 4.9). Если в бипирамидах верхняя пирамида распола-

гается четко над нижней, то в трапецоэдрах они связаны друг с другом

поворотом вокруг горизонтальной оси 2-го порядка и в проекции на

перпендикулярную главной оси плоскость оказываются повернутыми

одна относительно другой на произвольный угол, т. е. угол, не фикси-

рованный симметрическими операциями данного класса. Это являет-

ся признаком, облегчающим распознавание трапецоэдрических форм

в комбинационных кристаллах (рис. 4.9).

Глава

Простые формы кристаллов

183

В классе

четырехугольная форма грани общего положения «вы-

рождается»

разносторонний треугольник, являющийся гранью

так на-

зываемого ромбического тетраэдра,

котором

две

верхние грани отно-

сительно двух нижних повернуты вокруг вертикальной

оси 2-го

порядка

на произвольный угол (рис. 4.9в).

Поскольку верхняя пирамида многогранника

классах

может

быть повернута относительно нижней

по

часовой стрелке

или в

противо-

положном направлении,

то и

трапецоэдры соответственно могут быть

«правыми»

«левыми»,

т. е.

энантиолюрфными (рис.

4.9а, б).

Такие про-

стые формы встречаются лишь

классах,

не

содержащих операций сим-

метрии

рода

(см.

параграф

2.2.1).

В классе

нечетным порядком главной

оси

кроме тригональных

бипирамиды

трапецоэдра появляется новая простая форма, образо-

ванная гранями, равнонаклонными

эквивалентным горизонтальным

осям

, т. е.

каждая верхняя грань расположена симметрично относи-

тельно двух нижних граней (позиция

6 на

рис.

4.36).

Такая частная про-

стая форма

—

как бы

«симметризированный трапецоэдр»

—

носит название

ромбоэдр,

что

связано

формой граней этой простой формы

виде ром-

бов (рис.

4.96). В

классах

Ц, и D

грани, расположенные симметрично

от-

носительно двух нижних, оказываются гранями общего положения,

так

как

они

хотя

равнонаклонны,

но к

неэквивалентным осям

2-го

порядка;

Рис.

4.9.

Простые формы класса

и их

стереограммы: правый

левый тригональные

трапецоэдры

(а),

ромбоэдр (симметризованный трапецоэдр)

(б) и

класса

левый

и правый ромбические тетраэдры («вырожденные» дигональные трапецоэдры)

(в)

184

Кристаллография

кристаллохимия

отсюда названия образованных такими гранями общих простых форм

—

трапецоэдры — соответственно тетрагональный

гексагональный.

В соответствии

названиями общих простых форм классы

назы-

вают п-гоналъно-трапецоэдрическими. Класс

обычно называютромбо-

тетраэдрическим.

4.2.5.

Простые формы кристаллов

классах

2п

= Ф

Кристаллографическими классами,

не

повторяющими

уже

рассмо-

тренные комбинации элементов симметрии, будут

= £

С,

= <t

L.,C. Размножив грани, перпендикулярные

или

параллельные главной

оси, убеждаемся,

что

интересной

указанных классах будет лишь общая

по-

зиция исходной грани. Зеркальный поворот располагает верхние грани сим-

метрично относительно нижних.

классе

это не что

иное, как ромбоэдр

(рис.

4.10а), выведенный ранее

как

частная форма

классе

(рис.

4.96).

В классе5

(

получаемчетырехгранник,вкоторомдвеверхниеграниразвернуты

относительно двух нижних

на

90°,

—

тетрагональный тетраэдр;

его

грани

—

равнобедренные треугольники (рис.

4.106).

Следует отметить, что, несмотря

на

то что

ромбоэдр

тетрагональный тетраэдр получены

как

общие простые

формы

классах

и 5,

соответственно,

их

собственная симметрия значи-

тельно выше

описывается

для

ромбоэдра группой симметрии £

ЗР

= D,

, а для

тетрагонального тетраэдра

—

£,2Ь

2Р

= = D

. В

классе S,

(только

с центром инверсии) имеются лишь общие простые формы

—

пинакоиды,

об-

разованные двумя параллельными гранями.

Рис.

4.10.

Общие формы классов

: а —

ромбоэдр (класс

);

—

тетрагональный тетраэдр (класс

5,)

Очевидно,

что

класс

должен называться ромбоэдрическим, класс

—

тетрагоиально-тетраэдрическим,

класс

—

пинакоидалъным.

Глава

Простые формы кристаллов

185

4.2.6.

Простые формы кристаллов

классах

Dn6 = &2nnLj\P^

В классах

nrl

ромбоэдр

(D.

) и

тетрагональный тетраэдр

2rl

)

ока-

зываются

(в

отличие

от

подобных простых форм

классах

и S

со-

ответственно) частными формами,

так как их

грани перпендикулярны

плоскостям симметрии. Будучи выведенными

общее положение, грани

этих простых форм удваиваются

—

преломляются, образуя новые про-

стые формы

—

п-гоиалъные скаленоэдры (греч. скалена

—

разносторон-

ний треугольник) (рис.

4.11).

Причем каждая

из

верхних

пар

граней рас-

положена симметрично между двумя парами нижних граней.

Рис.

4.11.

Общие формы классов

Dj. а —

тригональный скаленоэдр (класс

£>

);

—

тетрагональный скаленоэдр (класс

)

В кристаллах возможны лишь

две

скаленоэдрические формы: три-

гональный скаленоэдр (преломленный ромбоэдр)

главной осью

(в классе

)

(рис.

4.11а) и

тетрагональный скаленоэдр (преломленный тет-

рагональный тетраэдр)

главной осью

= £Дв

классе

)

(рис.

4.116").

Классы

называют п-гоналъно-скаленоэдрическими.

Итак,

итоге нами выведены

простые формы кристаллов низшей

и средней категорий.

4.3. ВЫВОД ПРОСТЫХ ФОРМ КРИСТАЛЛОВ

КЛАССАХ ВЫСШЕЙ

КАТЕГОРИИ

КУБИЧЕСКОЙ СИНГОНИЙ

Простые формы кристаллов кубической сингоний,

так же как и

кри-

сталлов низшей

средней категорий, можно вывести, задавая исходную

грань

различные положения относительно элементов симметрии

со-

ответствующих классов. Однако из-за большого числа симметрических

186

Кристаллография

кристаллохимия

операций

кубических группах такой путь окажется слишком громозд-

ким. Более изящен

прост способ

Н. В.

Белова, предложившего осуще-

ствить вывод простых форм кристаллов кубической сингонии

как

про-

изводных

от

простейших основных форм (рис.

4.12).

4.3.1.

Основные простые формы

{100},

{111},

{1lT} и {110}

Основные простые формы кубических кристаллов —

это

простейшие

кристаллографические фигуры

несколькими осями высшего поряд-

ка,

не

имеющие осей

5-го

порядка:

куб

(гексаэдр), октаэдр, тетраэдр

ромбододекаэдр

(см. рис.

1.7 и

2.45).

Грани этих простых форм занимают

строго фиксированное положение,

как бы

подчеркивая основные осо-

бые направления классов кубической сингонии

—

три

координатные

оси

симметрии, четыре равнонаклонные

ним оси 3-го

порядка

шесть диа-

гональных особых направлений.

Грани, перпендикулярные координатным направлениям,

во

всех пяти

классах кубической системы образуют

куб

(гексаэдр)

символами граней

{100} (рис. 4.13).

Задание граней, перпендикулярных осям

3-го

порядка,

приводит

классах тЗт,

432, тЗ

биполярными осями

3-го

порядка

воз-

никновению октаэдра

—

простой формы

из

восьми треугольных граней

с символами

{111}.

классах

же 43т и 23

грани, перпендикулярные

те-

перь

уже

полярным тройным осям, образуют тетраэдр

четырьмя также

треугольными гранями

символами {111}и{пТ}. Четвертой постоянной

формой можно считать 12-гранную простую форму

—

ромбододекаэдр,

грани которого

символами

{110}

равнонаклонны

двум координатным

осям

параллельны третьей,

т.

е.

занимают

(как и

грани трех основных

форм) также строго фиксированное положение. Ромбододекаэдр,

так же

как

гексаэдр, встречается

во

всех пяти классах кубической сингонии.

Остальные простые формы кубических кристаллов выводятся

из пе-

речисленных основных форм путем вывода

их

из

строго фиксированных

Рис.

4.12.

Различные позиции граней

на

стереограмме кубических классов симметрии.

Грани основных простых форм:

— гексаэдра

(100),

2 —

октаэдра

или

тетраэдра

(111)

—

ромбододекаэдра

(110);

грани производных форм:

— (МО),

—

{hhl},

III

—

{hit),

IV-{hkl}(h>k>\)

Глава

Простые формы кристаллов

187

позиций, что выражается

«наращивании» на их гранях «пирамидок» —

двух-, трех-, четырех-

или

шестискатных «крыш», допускаемых пло-

скостной симметрией граней.

тЗт

432

тЗ

43т

;

-'7

Основные формы с постоянными символами

./'/

гексаэдр (к\

ООО)

октаэдр

\ (П7)

тетраэдр

\ -3

(721)

ромбододекаэдр

(гранатоэдр)

(770)

Производные формы

тритоп-тетрагексаэдр

Г\

(пирамидадышй куб)

тетра

то

н-

тетрагсксаэдр

(ЬЫ) (К/о

тетра гон -

три октаэдр

(24-транпый \ (24-транпы

Л дол ьтоэдр]

тригоп-

д и гексаэдр

(Ш)

(/</()

-У

тр и го п-тр ио кта э;\ р

(пирамидальный октаэдр)

(Ш)

(/•>;) ^

пепта

гон-

до декаэдр

(ЙОГ)

тетра гон-тритетрюдр

(12-гранный де.чьтсюдр)

(Щ) (Л>!)

Общие простые формы

(Ш)

•ИМ

тригоп-

тритетраэдр

(пирамида.

!!^

ним тетраэдр)

гексаоктаэдр пемтатогг-триоктаэдр дидодекаэдр

(= окта гексаэдр) (пентагом-тстраг-ексаэдр)

(24-фан1и>1Й осевмк)

гхжеатетраэдр пептаго!

t-'rpt-f

тетраэдр

(Пентагон- дигексаэдр)

(12-граппмй осешк)

Рис.

4.13. Схема вывода простых форм кристаллов кубической сингоний

188

Кристаллография

кристаллохимия

4.3.2.

Простые формы

{МО} -

производные куба (гексаэдра)

Если грань гексаэдра перевести

из

положения

(100) в

положение

(hkO), то ее

симметрия понизится либо

четыре, либо

в два

раза

и со-

ответственно увеличится

по

сравнению

числом граней гексаэдра

(6)

число граней простой формы:

четыре раза

классах тЗт,

432, 43т и в

два

—

классах

тЗ и 23.

Таким образом, вместо каждой квадратной гра-

ни гексаэдра появится либо четырехгранная пирамида, либо двухскатная

крыша (см. рис.

4.13).

Двадцатичетырехгранная

(6x4 = 24)

форма {hkO}

называется тригон-тетрагексаэдром\ Очень выразительно

классиче-

ское

ее

название

—

пирамидальный

куб

(рис. 4.146-Э).

Рис.

4.14.

Тригон-тетрагексаэдр

и его

генезис

классе

тЗт

Двенадцатигранная форма может быть названа соответственно

пен-

тагон-дигексаэдром,

так как ее

грани имеют форму неправильных пяти-

угольников,

но

поскольку по-гречески додека — двенадцать,

то эту

про-

стую форму обычно называют пентагон-додекаэдром (рис. 4.156-Э).

Рис.

4.15.

Пентагон-додекаэдр

и его

генезис

классе

тЗ

Четырехгранные пирамиды

двухскатные «крыши», образовавшиеся

на грани гексаэдра (куба), могут менять свою крутизну

зависимости

от

Названия большинства производных простых форм кристаллов кубиче-

ской сингонии строятся

по

следующей схеме:

• сначала характеризуется

форма грани: тригон —

треугольная,

тетра-

гон —

четырехугольная,

Пентагон —

пятиугольная;

• затем фиксируется количество граней, заменивших исходную грань

основной простой формы;

• указывается название простой формы,

на

основе которой выводится

по-

лученная производная форма. Например,

тригон-тетрагексаэдр —

про-

стая форма

гранями треугольной формы, грань исходной формы

—

гексаэдра —

учетверилась

и т. д.

Глава

Простые формы кристаллов

189

соотношения индексов

hnk.Uo

мере перемещения проекции грани

от по-

ложения

(100) к (110)

индексы

h и k

будут

все

более выравниваться

и при

h = k (МО) = (110)

возникнет одна

из

основных форм — ромбододекаэдр.

При этом вначале индекс

будет существенно больше

(например, (МО)

(910)). В

результате этого облик всей формы окажется кубическим,

так

как

пирамиды

на

грани куба будут очень пологими.

При

сближении

значенийhiik(например,

(910) -> (920) -> (940) -> (980) -» (990))

пира-

миды будут становиться

все

круче

и при

равенстве

h = k в

первом случае

(рис.

4.14Э,

е)

стереографические проекции двух треугольных граней

предельно крутого тетрагексаэдра сольются

одну ромбовидную грань:

(980)

—>

(ПО)

<—

(890)

(количество граней

при

этом сократится вдвое

—

24 : 2 = 12), во

втором

—

грани пятиугольной формы трансформируются

в ромбы

(рис.

4.15Э,

е), но

количество граней

(12) при

этом сохранится.

В итоге грани полученного ромбододекаэдра окажутся равнонаклонны

к двум координатным осям

параллельны третьей,

т. е.

займут строго

фиксированное положение.

4.3.3. Простые формы

{Ал/}

(/?>/)-

производные октаэдра

тетраэдра

Если

качестве исходной взять грань октаэдра

или

тетраэдра

симво-

лом

(111) и

сместить

ее в

направлении

грани ромбододекаэдра

(110), то

символ такой грани

общем виде запишется

как (hhl)

(где

h >

I), количество

же граней

при

этом увеличится под действием

оси 3-го

порядка

в три

раза.

В классах

тЗт, 432, тЗ

вместо грани октаэдра возникнет трехгран-

ная пирамидка

из

треугольных граней,

форма полученного 24-гранни-

ка

•

3 = 24)

будет называться тригон-триоктаэдром

(или

пирамидаль-

ным октаэдром) (рис.

4.16 б-г).

Вместо грани тетраэдра

классах

43т и

образуется пирамидка

из

четырехугольных граней, отсюда обычное

название этой 12-гранной

•

3 = 12)

простой формы — тетрагон-три-

тетраэдр (рис. 4.176-Э),

но ее

также называют 12-гранным делътоэдром,

так

как

грань состоит

как бы из

двух «дельт».

б в г д

Рис.

4.16.

Тригон-триоктаэдр

и его

генезис

классе

тЗт

Предельное увеличение крутизны пирамидок этих производных форм

скажется

на

изменении символов

их

граней:

(111)

—>

(998) —> (994)

—»

(991) -> (110) и в

конечном итоге приведет

к уже

известной простой

форме

постоянным символом

—

ромбододекаэдру (рис.

4.16 и 4.17).