Егоров-Тисменко Ю.К. Кристаллография и кристаллохимия
Подождите немного. Документ загружается.

190
Кристаллография и кристаллохимия
а б в г д
е
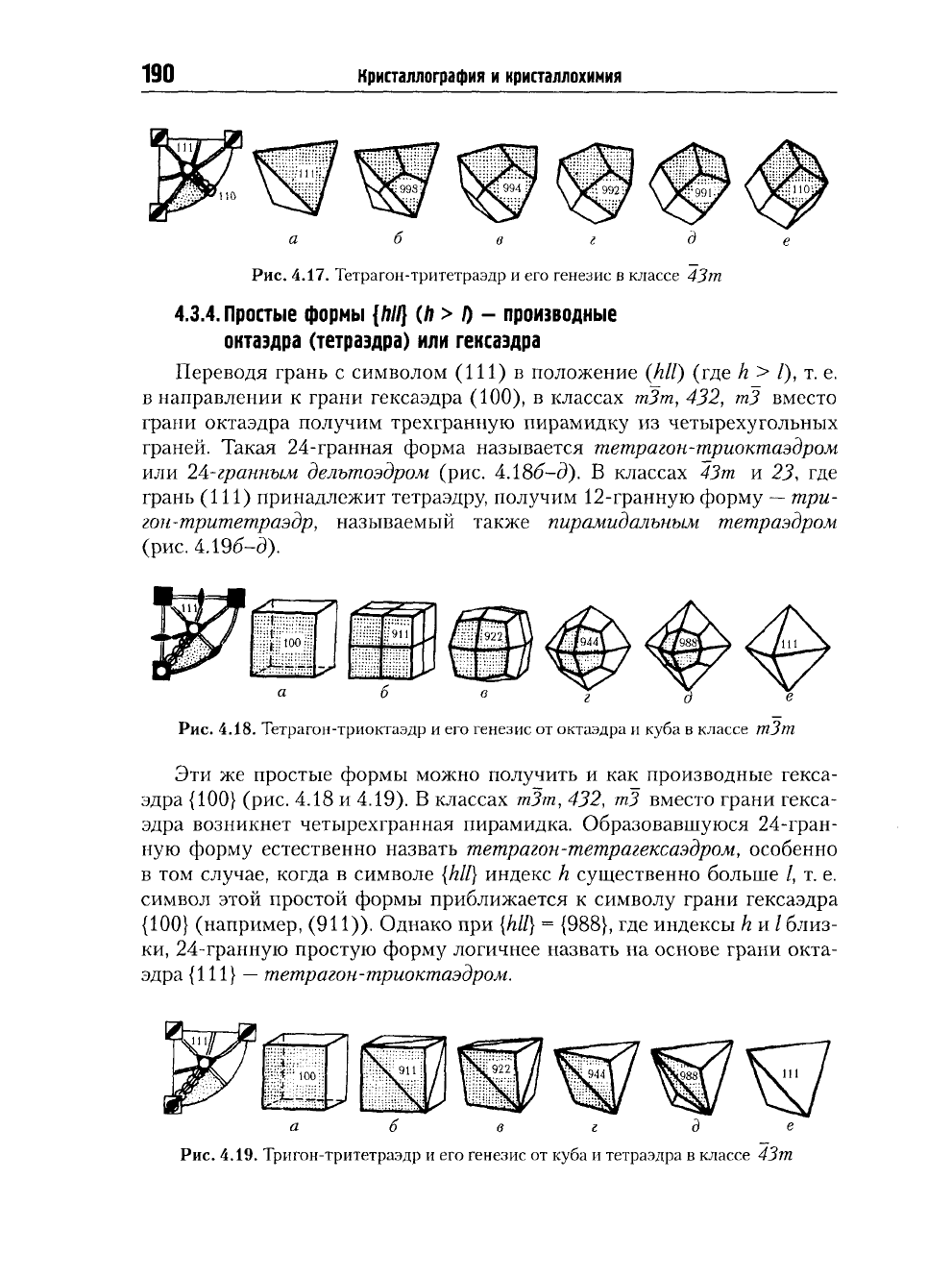
Рис.
4.17. Тетрагон-тритетраэдр и его генезис в классе 43т
4.3.4.
Простые формы {hll} (ft > I) - производные
октаэдра (тетраэдра) или гексаэдра
Переводя грань с символом (111) в положение (hll) (где h > I), т. е.
в направлении к грани гексаэдра
(100),
в классах тЗт, 432, тЗ вместо
грани октаэдра получим трехгранную пирамидку из четырехугольных
граней. Такая 24-гранная форма называется тетрагон-триоктаэдром
или 24-гранным делътоэдром (рис. 4.186-д). В классах 43т и 23, где
грань (111) принадлежит тетраэдру, получим 12-гранную форму — три-
гон-тритетраэдр, называемый также пирамидальным тетраэдром
(рис.
4.195-Э).
Рис.
4.18. Тетрагон-триоктаэдр и его генезис от октаэдра и куба в классе тЗт
Эти же простые формы можно получить и как производные гекса-
эдра {100} (рис. 4.18 и
4.19).
В классах тЗт, 432, тЗ вместо грани гекса-
эдра возникнет четырехгранная пирамидка. Образовавшуюся 24-гран-
ную форму естественно назвать тетрагон-тетрагексаэдром, особенно
в том случае, когда в символе {hll} индекс h существенно больше /, т. е.
символ этой простой формы приближается к символу грани гексаэдра
{100} (например,
(911)).
Однако при {hll} =
{988},
где индексы h и / близ-
ки,
24-гранную простую форму логичнее назвать на основе грани окта-
эдра {111}
—
тетрагон-триоктаэдром.
а б в г д е
Рис.
4.19. Тригон-тритетраэдр и его генезис от куба и тетраэдра в классе 43т

Глава
4.
Простые формы кристаллов
191
В классах
43т и 23
вместо грани гексаэдра образуется двухскатная
«крыша»
(рис. 4.19), и
возникшую
в
этом случае форму можно было
бы
назвать тригон-дигексаэдром (особенно если
в ее
символе
h » /).
Одна-
ко наиболее распространенное название этой простой формы — тригон-
тритетраэдр,
— по
существу, оправдывается лишь
в том
случае, когда
в символе {hll}
h~l.
4.3.5. Общие простые формы кристаллов кубической сингонии
- {Щ
Класс
тЗт.
Общую простую форму
в
этом классе можно получить
либо
на
основе грани октаэдра, либо грани гексаэдра
(рис. 4.20).
Если
в общее положение
(hkl)
перевести грань октаэдра
(111), то она под
дей-
ствием диагональных плоскостей симметрии ушестерится,
в
результа-
те чего возникнет 48-гранник
(8 • 6 = 48) (рис.
4.20Э). Если
же
данную
простую форму получать
на
основе гексаэдра
(100), то на
каждой
его
гра-
ни возникнет восьмигранная пирамида,
т. е.
вновь получим 48-гранник
(6 • 8 = 48) (рис. 4.206).
Однако подобные реализованные
в
кристаллах
простые формы,
как
правило, имеют октаэдрический габитус
(h~k~ /),
поэтому общепринятое название этой простой формы
—
гексаоктаэдр,
хотя
при
{hkl},
где (k ~ I) « А,
предпочтительнее было
бы
назвать
эту
форму октагексаэдром.
Как
видим,
в
характеристике формы грани дан-
ной простой формы
в
приставке тригон
нет
надобности,
так как эта
един-
ственная 48-гранная простая форма может иметь только треугольные
грани.
Рис.
4.20.
Общая форма
в
классе
тЗт
— сорокавосьмигранник
:
= октагексаэдр —
и его
генезис
гексаоктаэдр
=
Голоэдрический (полносимметричный) класс
тЗт
называют клас-
сом сорокавосьмигранника,
или
гексаоктаэдрическим.
Класс
43т.
Общую простую форму
в
этом классе можно получить,
переведя грань тетраэдра
(111) в
общее положение,
при
этом
на
треу-
гольной грани тетраэдра возникнет шестигранная пирамидка. Отсю-
да наиболее распространенное название этой формы
—
гексатетраэдр
(рис.
4.21г,
д),
хотя
эту
простую форму можно считать производной гек-
саэдра
и
называть тригон-тетрагексаэдром (особенно
при (h = /) « h)
(рис.
4.216, в),
однако
это
название
уже
использовано
в
характеристике
частных простых форм.

192
Кристаллография и кристаллохимия
Класс 43т называется гексатетраэдрическим.
Рис.
4.21. Общая простая форма в классе 43т — гексатетраэдр — и его генезис
Класс тЗ. Общую форму этого класса логично рассматривать как
«вторичную» производную от гексаэдра: сначала грань куба (100) выве-
сти на координатную плоскость, получив при этом пентагон-додекаэдр
(hkO) (рис.
4.226,
в), и затем уже вывести ее в общее положение. В ре-
зультате пятиугольная грань пентагон-додекаэдра удвоится (сломается)
координатной плоскостью, что приведет к 24-граннику — преломлен-
ному пентагон-додекаэдру, который обычно называют дидодекаэдром
(рис.
4.22г-е). Эту же форму можно считать и производной октаэдра,
получив вместо одной треугольной грани три четырехугольных. Одна-
ко название тетрагон-триоктаэдр и в этом случае оказывается уже ис-
пользованным для частной простой формы.
Класс тЗ называют дидодекаэдрическим.
Рис.
4.22. Общая простая форма класса тЗ — дидодекаэдр — и его генезис
Классы 432 и 23. Это старшие (наиболее симметричные) кристалло-
графические осевые классы. Общие формы в кристаллах такой симметрии
можно получить на основе грани куба, октаэдра или тетраэдра. При этом
в классе 432 вместо грани гексаэдра возникают четырехгранные пирамид-
ки с пятиугольными гранями (рис. 4.23в) либо трехгранные вместо грани
октаэдра (рис. 4.23г). Полученная 24-гранная форма (в классе 432) называ-
ется пентагон-триоктаэдром (2А\-гранным гироэдром или осевиком, от греч.
гира — ось) (рис. 4.23) или, при (k ~ I) « h, — пентагон-тетрагексаэдром.
В классе 23 грань куба трансформируется в две также пятиугольные
грани. Если как вариант эту простую форму получать на основе грани те-
траэдра, то вместо одной его грани возникнет пирамидка из трех граней,
т. е. 12-гранный осевик, или гироэдр, с современным названием пентагон-
тритетраэдр (рис. 4.24г, д). Если же данную простую форму рассматри-
вать как производную от гексаэдра при (k ~ I) « h, ее можно было бы
назвать «несимметричным» пентагон-дигексаэдром (рис. 4.24в).

Глава 4. Простые формы кристаллов
193
Рис.
4.23. Общая простая форма класса 432
—
пентагон-триоктаэдр (24-гранный
осевик) — и его генезис
Рис.
4.24. Общая простая форма класса 23
—
пентагон-тритетраэдр (12-гранный
осевик) и его генезис
Класс 432 называют пентагон-триоктаэдрическим, а класс 23 — пен-
тагон-тритетраэдрическим.
Вывод 15 простых форм кубической сингонии удобно представить
в виде схемы, изображенной на рис. 4.13.
При определении названий простых форм кристаллов кубической
сингонии, в которых используются характеристики форм граней — при-
ставки «тригон-», «тетрагон-», «Пентагон-», а также в кристаллах низшей
и средней категорий
—
приставки «ромбо-», «трапеца-», «скалена-» и т. д.,
надо иметь в виду, что такое название составить легко, если в огранке
кристалла участвуют грани лишь одной простой формы. Если же кри-
сталл комбинационный, т. е. является комбинацией нескольких простых
форм, то истинные очертания граней каждой простой формы могут быть
сильно искажены. В этом случае их «ложная» форма не может входить
в название той или иной простой формы (рис.
4.25).
В таких случаях
надежнее обратиться к стереографической проекции комбинационного
кристалла и с ее помощью получить сведения и о симметрии кристалла,
и о взаимном расположении граней каждой простой формы, участвую-
щей в огранке кристалла, что позволит правильно составить название
той или иной простой формы.
Как было показано выше, одна и та же простая форма может встре-
чаться в различных классах симметрии, причем в одном классе форма
может быть частной, а в другом — общей (например, ромбоэдр в классе
Зт
—
частная форма, а в классе J
—
общая). Поэтому, естественно, грани
одной (по названию) формы могут отличаться по своей симметрии. На-
пример, диэдр может быть осевым или плоскостным (см. рис. 4.5), а мо-
ноэдр может быть реализован в десяти различных классах. У реальных
кристаллов это различие выступает при изучении физических свойств
7 - 98.

194
Кристаллография
и
кристаллохимия
поверхностей граней,
и в
первую очередь фигур
их
роста
(см.
пара-
граф
5.8.1),
растворения, травления
и
других особенностей скульптуры
граней. Например, гексаэдры,
как
отметил
А. В.
Шубников, могут иметь
различную
по
симметрии штриховку граней
в
соответствии
с
пятью
ви-
дами симметрии кубической сингонии (рис.
4.26).
Рис.
4.25.
Переход
от
простой формы ромбододекаэдра через
его
комбинации
с гексаэдром
и
тетраэдром
к
простой форме — тетраэдру, иллюстрирующий
искаженные очертания граней простой формы
в
комбинационном кристалле
Учет симметрии простых форм,
а
следовательно,
и их
физических
свойств позволил кристаллохимику Г.
Б.
Бокию
(1909-2002)
увеличить
общее число простых форм
с 47 до 146
физически различных форм,
а
при учете энантиоморфных
пар
—
до 193.
Если
же
учесть
тот
факт,
что
в классах
с
полярными направлениями параллельные друг другу грани
с символами
(hkl) и ( hkl)
могут
не
выводиться друг
из
друга операци-
ями симметрии класса
и
образовывать
так
называемые положительные
и отрицательные формы,
то
число простых форм будет
318
(напри-
мер,
грани положительного
(111) и
отрицательного
(ТТТ)
тетраэдров
в классе
23).
тЗт
432 тЗ 43т 23
Рис.
4.26.
Собственная симметрия граней пяти разновидностей куба, принадлежащих
пяти классам кубической сингонии
(по А. В.
Шубникову)

Глава 4. Простые формы нристаллов
195
4.4. ГОНИОМЕТРИЯ
Первый эмпирический закон кристаллографии — закон постоян-
ства углов, открытый еще в
XVII
в. Н. Стеноном, послужил основой и
первого кристаллографического метода — гониометрии (от греч. гониа
(ymvm)
—
угол, ретро — меряю) — метода измерения углов между гра-
нями кристаллов, долгое время являвшегося основным при изучении
огранки кристаллов. С помощью первого примитивного приспособле-
ния
—
прикладного гониометра М. Каранжо, сконструированного в 1772 г.
(см.
рис.
1.23),
можно измерять углы между гранями достаточно круп-
ных (более 0,5 см) и хорошо ограненных кристаллов с точностью до 0,5°.
Не повысили точность измерения и более совершенные модели приклад-
ных одно- и двукружных гониометров (рис.
4.27),
недостатком которых,
в частности, явились жесткая фиксация исследуемого кристалла в пер-
вом случае, а следовательно, необходимость его переклеивания для из-
мерения углов между гранями разных поясов, а также требования к раз-
меру кристаллов. Такие гониометры применяются в тех случаях, когда
большой размер кристалла или несовершенство поверхности его граней
не позволяют провести более точные измерения.
Рис.
4.27. Прикладной двукружный гониометр Гольдшмидта
Позднее были созданы оптические отражательные гониометры, с по-
мощью которых стало возможным исследовать более мелкие кристалли-
ки с блестящими гранями. Принцип работы на таком гониометре, схема
которого показана на рис. 4.28, заключается в получении последователь-
ных отражений световых лучей от граней кристалла и в их регистрации.
Узкий пучок света, пройдя коллиматор, падает на грань кристалла. Если
отразившийся луч попадает в зрительную трубу, это значит, что нормаль
fuV,
к отражающей грани кристалла (рис. 4.29) совпала с биссектрисой
7*

196
Кристаллография
и
нристаллохимия
угла между падающим
и
отраженным
от
грани кристалла лучами.
За-
фиксировав положение лимба
(рис. 4.28) в
момент отражения луча,
а
затем вращением лимба установив
в
отражающее положение соседнюю
грань кристалла
и
зафиксировав
это
положение, можно измерить угол
(3
между нормалями
и
JV
2
к
отражающим граням
a
f
и а
2
, а
следовательно,
и угол между гранями.
Если гониометр снабжен двумя лимбами
—
вертикальным
и
гори-
зонтальным, каждый
со
своей осью вращения,
то в
результате измерения
любая грань кристалла может быть зафиксирована соответствующими
значениями сферических координат
ф по
горизонтальному
и р по
верти-
кальному лимбам.
Оба
лимба снабжены нониусами, позволяющими
по-
лучать отсчеты
с
точностью
до 0,5'.
Большой вклад
в
развитие методики гониометрических исследова-
ний кристаллов
и
использование
их
результатов внесли
Н. И.
Кокшаров
(1818-1892), В.
Голъдишидт
(1853-1933),
составивший многотомный
Кристалл
Свет
Коллиматор
Рис.
4.28.
Принципиальная схема действия отражательного гониометра
/
\
/
Рис.
4.29.
Соотношение углов между гранями кристалла
и
нормалями
к ним

Глава
4.
Простые формы кристаллов
197
«Атлас форм кристаллов»,
Е. С.
Федоров, внедривший вместе
с
В. Гольд-
шмидтом
в
1893 г.
в
практику двукружный отражательный (теодолит-
ный) гониометр,
а
также
Е. Е.
Флинт
(1887-1978).
В настоящее время широко используются
две
модели двукружных
от-
ражательных гониометров: ГД-1
и
ZRG-3,
а
также фотогониометры,
в
ко-
торых отраженные
от
граней кристалла лучи фиксируются
на
пленку.
Полученные гониометрические данные
—
сферические координаты
ф
и
р
каждой грани кристалла
—
позволяют,
с
одной стороны, рассчитать
основные характеристики кристаллов:
их
симметрию, символы граней
и
ребер
и в
конечном счете геометрические константы кристаллов
(см. па-
раграф
3.1),
а с
другой, построив гномостереографическую проекцию
ис-
следуемого кристалла,
на ее
основе воссоздать (вычертить)
его
общий
вид.
Ниже
в
качестве примера приведен один
из
основанных
на
законе
по-
ясов приемов вычерчивания кристалла, представляющего собой комби-
нацию двух простых форм
—
куба
и
ромбододекаэдра (рис.
4.30).
На первом этапе строят ортогональную проекцию кристалла (рис.
4.306),
т.
е. вид на
кристалл сверху вдоль
оси
с,
для
чего
на
стереограмме (рис. 4.30а)
проводят зональные линии
—
дуги больших кругов
(c^-c
v
с
2
-с
А
,
d-d
T
d
5
-d
(
),
являющиеся гномостереографическими проекциями ребер,
по
которым
пересекаются грани, принадлежащие каждой зоне. Перпендикуляры
к
диаметрам зональных линий стереограммы будут проекциями указанных
ребер
на
плоскость чертежа. Вначале проводят линии (проекции верти-
кальных граней), оконтуривающие ортогональную проекцию кристалла,
т.
е.
линии
с,
и с
ч
(рис.
4.306)
(проведенные перпендикулярно диаметру
c-c.
v
рис.
4.30а), линии
с
2
и с
к
(рис.
4.306)
(перпендикулярные диаметру
с.-с
А
, рис. 4.30а),
d
s
и d
7
,
d
r}
и
d
6
,
перпендикулярные диаметрам
d
]
~d
7
, d
5
-d
G
соответственно. Затем
в
виде взаимно параллельных линий проециру-
ются ребра между гранями каждой зоны (например, между гранями
c
t
, d,
с,
d
v
с
3
и
т.
д.),
при
этом следует учитывать симметрию
и
относительные
размеры граней.
В
результате получим ортогональную проекцию кри-
сталла (рис.
4.306).
Чтобы получить полную информацию
о
внешнем виде кристалла,
не-
обходимо
его
представить
в
выгодном ракурсе,
так,
чтобы были отчетли-
во видны наиболее характерные особенности огранки.
Для
этого нужно
выбрать иную плоскость проекций (плоскость, перпендикулярно кото-
рой рассматривается кристалл) —
это
и
будет аксонометрическая проек-
ция (рис. 4.30в). Обычно
в
качестве плоскости проекции выбирают такую
плоскость, сферические координаты полюса
Р
которой
ф =
70°, р = 80°,
при этом полюс
Р не
должен
ни
совпадать
с
проекцией какой-либо грани,
ни попадать
на
зональные дуги. После этого строится стереографическая
проекция данной плоскости
(см.
параграф
2.3.2)
— дуга большого круга
АВ (рис. 4.30а).

198
Кристаллография
и кристаллохимия
Рис.
4.30. Построение ортогональной и аксонометрической проекций
кубического
кристалла по его стереограмме (по И. Костову)
Для определения направления ребра между двумя гранями кристал-
ла (например, d и d
A
) на аксонометрической проекции (рис. 4.30е) полюс
плоскости проекции
—
точку Р
—
соединяют прямой с точкой пересечения
(М) дуги АВ и зональной дугой, проведенной через искомые грани (d и d
A
),
и продолжают эту прямую до пересечения с основным кругом проекции (по-
лучают точку М'). Нормаль к линии, проведенной через полученную точку
М на окружности с центром круга проекции (с), и будет направлением ис-
комого ребра между гранями (d и d
A
), принадлежащими указанной зоне.
Построение аксонометрической проекции удобно начать с определе-
ния направления ребер вертикального пояса между гранями
d
s
,c
v
d
v
c
y
d
5
(рис.
4.30Й),
совпадающего с направлением перпендикуляра к диаметру
АВ.
После этого через каждую вершину ортогональной проекции про-
водят серию прямых, параллельных полученному направлению и лими-
тирующих длины ребер между соответствующими гранями кристалла.
При этом крайняя левая точка аксонометрической проекции находится
на перпендикуляре к диаметру АВ, проходящем через крайнюю левую
точку начерченной ранее ортогональной проекции. Проведя аналогич-
ные построения для всех поясов, получим аксонометрическую проекцию
исследуемого кристалла (рис. 4.30в).
Полученная проекция является идеализированным изображением
кристалла и, к сожалению, не отражает всех особенностей реальной его
огранки: степени развития граней, искажения истинной симметрии и т. д.

Глава 4. Простые формы кристаллов
199
Поэтому иногда полезно обратиться к фотографированию кристалла
в наиболее благоприятном ракурсе с последующей дешифровкой ребер
и нанесением символов его граней.
В итоге гониометрический метод исследования кристаллов позво-
ляет путем сравнения измеренных углов между их гранями с данными,
собранными в таблицы справочников, определить принадлежность ис-
следуемого кристалла к тому или иному веществу. Однако проведение
таких исследований возможно лишь для достаточно хорошо ограненных
кристаллов. С развитием рентгенографических исследований метод го-
ниометрии больше не является основным в геометрической кристалло-
графии, однако он сохраняет свое значение при изучении морфологии
кристаллов и их роста, в технической кристаллографии, в минералогии,
в геммологии, а также находит ряд других применений. В сочетании
с анализом химического состава гониометрические данные кристаллов
и микрокристаллов используют для определения фазового состава син-
тетических и природных веществ.
