Егоров-Тисменко Ю.К. Кристаллография и кристаллохимия
Подождите немного. Документ загружается.


so
Кристаллография и кристаллохимия
а б в
Рис.
2.2. Примеры конгруэнтного (а) и зеркального (энантиоморфного) (б, о)
равенства фигур
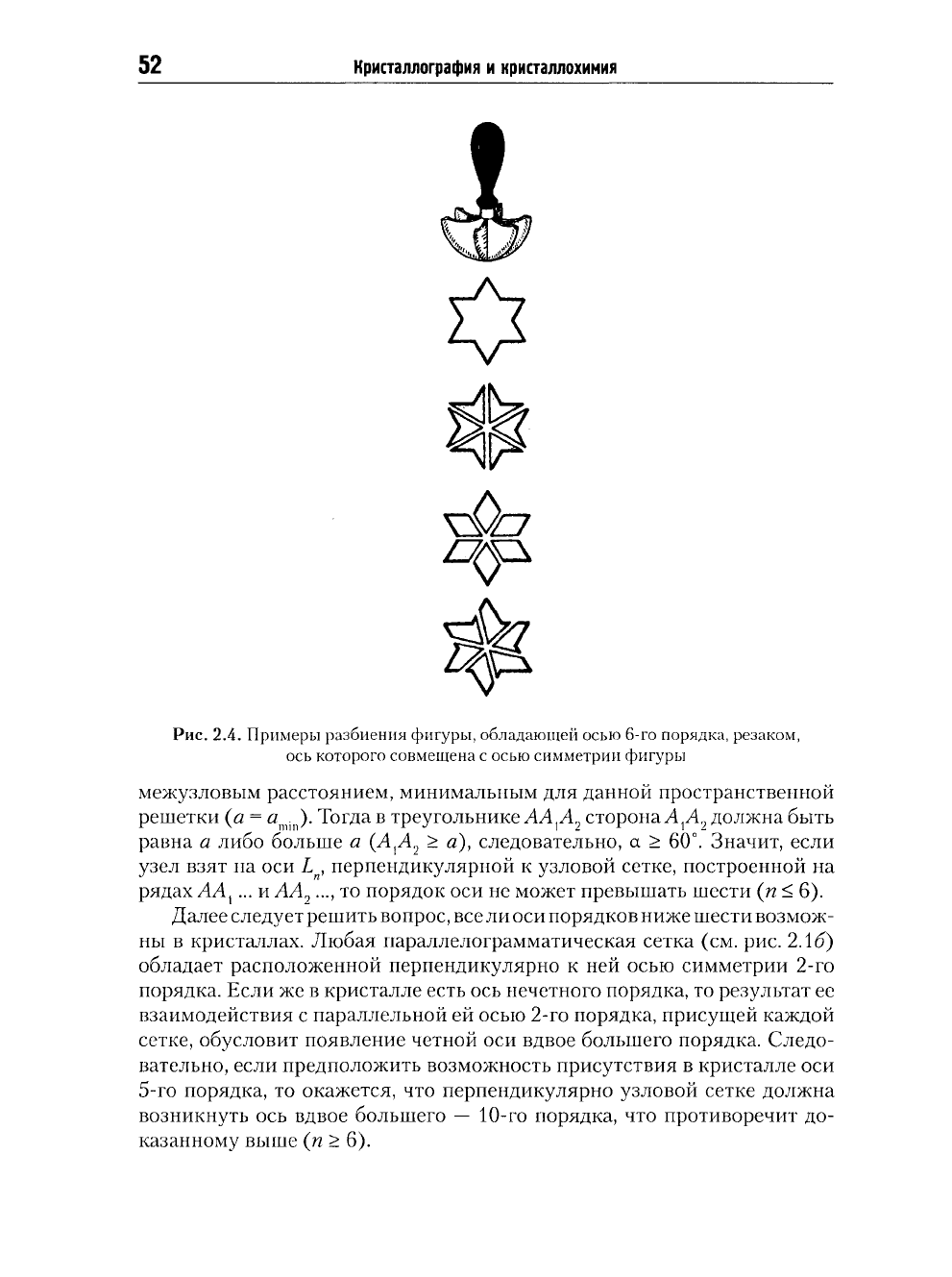
быть рассечена на п конгруэнтно равных частей бесконечным числом
способов (рис. 2.4).
В учебной символике — символике Браве
—
оси симметрии обознача-
ются как L
n
, где подстрочный цифровой индекс п указывает на порядок
оси
1
. Графически оси симметрии обозначаются многоугольниками:
L
(
.
— ф>
—
•, /_
3
— L
2
— ф (сферический двуугольник (фюзо)).
Ось 1-го порядка Z, графического значка не имеет.
В геометрических фигурах возможны оси симметрии любого поряд-
ка. В кристаллических многогранниках порядок осей ограничен числами
п =
1,2,3,4,6,
т. е. в кристаллах невозможны оси 5-го и выше 6-го порядков.
В этом суть основного закона симметрии кристаллов, установленного эм-
пирически, но впоследствии подтвержденного «решетчатым» строением
кристаллов.
Доказательством этого закона может служить то, что любая узло-
вая сетка всякой пространственной решетки, представляющая собой
параллелограмматическую систему, не может обладать осью 5-го или
больше 6-го порядка, ибо нельзя правильными пяти- или п-угольни-
ками (где п > 6) выполнить все пространство без остатка. Таким об-
разом, пространственная решетка кристалла может быть инвариантна
только относительно поворотов вокруг осей кристаллографических
порядков, т. е. допускает оси симметрии лишь 1, 2, 3, 4 и 6-го поряд-
ков.
В этом состоит основное отличие симметрии кристаллических
веществ от симметрии живых организмов, в которых возможны оси
5-го порядка.
Н. В. Белов предложил иное, выгодно отличающееся от других до-
казательство основного закона, базирующееся на некоторых интересных
и важных особенностях кристаллической пространственной решетки.
1
В старых учебниках поворотные оси симметрии обозначены буквой G
—
от
введенного П. Ниггли термина
Gyre
—
поворотная ось (от греч. у6ро(
—
круг).
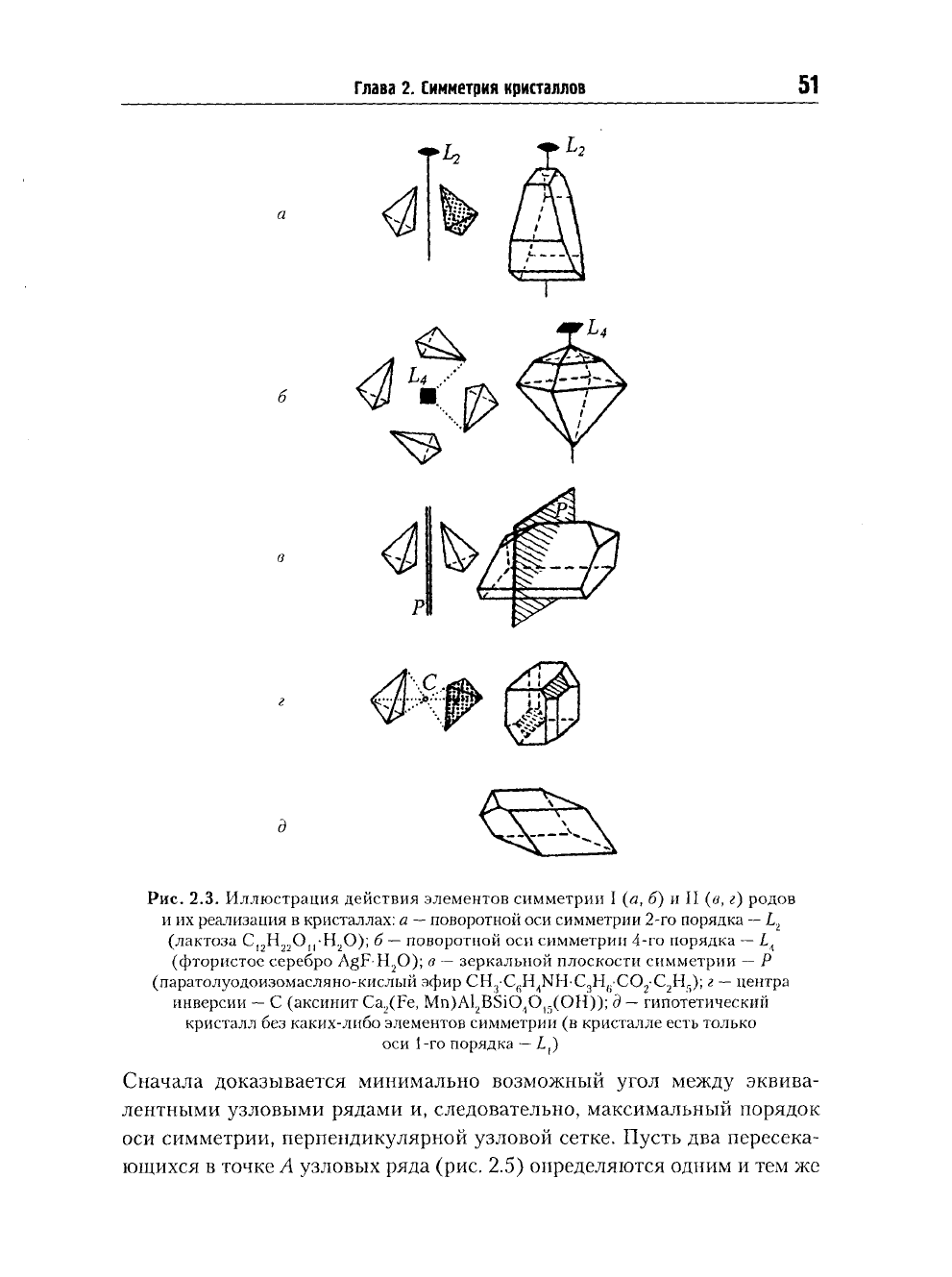
Глава 2. Симметрия кристаллов
51
Рис.
2.3. Иллюстрация действия элементов симметрии I (а, б) и II (а, г) родов
и их реализация в кристаллах: а
—
поворотной оси симметрии 2-го порядка
—
L
2
(лактоза С
12
Н
22
О
н
Н
2
0); б
—
поворотной оси симметрии 4-го порядка — 1
4
(фтористое серебро AgFH
2
0); в — зеркальной плоскости симметрии — Р
(паратолуодоизомасляно-кислый эфир
CH.
!
C
6
H
<
NHC
3
H
(
,C0
2
-C
2
H
r)
);
г — центра
инверсии — С (аксинит
Ca
2
(Fe,
Mn)Al
2
BSi0
1
0
|
-(OH)); д — гипотетический
кристалл без каких-либо элементов симметрии (в кристалле есть только
оси 1-го порядка
—
L
t
)
Сначала доказывается минимально возможный угол между эквива-
лентными узловыми рядами и, следовательно, максимальный порядок
оси симметрии, перпендикулярной узловой сетке. Пусть два пересека-
ющихся в точке А узловых ряда (рис. 2.5) определяются одним и тем же
52
Кристаллография и кристаллохимия
Рис.
2.4. Примеры разбиения фигуры, обладающей осью 6л"0 порядка, резаком,
ось которого совмещена с осью симметрии фигуры
межузловым расстоянием, минимальным для данной пространственной
решетки (а =
fl
mjn
).
Тогда в треугольнике ЛЛ
]
Л
2
сторона Л
(
Л
2
должна быть
равна а либо больше а (Л,Л
2
> а), следовательно, а > 60°. Значит, если
узел взят па оси L
n
, перпендикулярной к узловой сетке, построенной на
рядах ЛЛ
1
... и ЛЛ
2
то порядок оси не может превышать шести (п < 6).
Далее следует решить вопрос, все ли оси порядков ниже шести возмож-
ны в кристаллах. Любая параллелограмматическая сетка (см. рис. 2.16)
обладает расположенной перпендикулярно к ней осью симметрии 2-го
порядка. Если же в кристалле есть ось нечетного порядка, то результат ее
взаимодействия с параллельной ей осью 2-го порядка, присущей каждой
сетке, обусловит появление четной оси вдвое большего порядка. Следо-
вательно, если предположить возможность присутствия в кристалле оси
5-го порядка, то окажется, что перпендикулярно узловой сетке должна
возникнуть ось вдвое большего — 10-го порядка, что противоречит до-
казанному выше (п > 6).

Глава 2. Симметрия кристаллов
53
Рис.
2.5. К доказательству невозможности наличия в пространственной решетке
кристаллов осей симметрии 5-го и выше 6-го порядков
Таким образом, пространственная решетка кристалла, а следователь-
но,
и кристаллический многогранник допускают оси симметрии лишь
следующих порядков: п = 1, 2, 3, 4 и 6', при этом оси 1-го и 2-го порядков
принято считать осями низшего порядка (ось 1-го порядка задает поворот
на 360°, т. е. операцию идентичности, или тождественности), оси поряд-
ка выше 2-го — осями высшего порядка.
При описании операций симметрии к обозначениям осей симметрии
часто добавляют показатель степени, указывающий на число проведен-
ных операций
—
в данном случае на число элементарных поворотов в на-
правлении против часовой стрелки. Знак «минус» при показателе степе-
ни указывает на поворот в противоположном направлении
—
по часовой
стрелке. Например, если /_|.
—
один поворот на 60° против часовой стрел-
ки вокруг оси 6-го порядка, Ц. — два таких поворота, то Ц} — один по-
ворот на 60° по часовой стрелке, результат которого соответствует пяти
поворотам (60 • 5 = 300°) в обратную сторону — I"
1
= Ц.. Таким образом,
Ц. = = ц* = ц
2
, a
Lg
= I, — операция идентичности или тождественности
(фигура остается на месте).
2.2.2.
Элементы симметрии II рода
К элементам симметрии II рода относятся: зеркальная плоскость,
центр инверсии и сложные элементы симметрии — зеркально-поворот-
ные и инверсионные оси.
Зеркальная плоскость симметрии. Представление о зеркальной пло-
скости как элементе симметрии сложилось с незапамятных времен. Он
задает операцию отражения, при которой правая часть фигуры (или
1
В отличие от кристаллов живые организмы обладают осями некристалло-
графических порядков. Н. В. Белов писал: «Можно думать, что пятерная ось яв-
ляется у мелких организмов своеобразным инструментом борьбы за существо-
вание, страховкой против окаменения, против кристаллизации, первым шагом
которой была бы их "поимка" решеткой».

54
Кристаллография
и
кристаллохимия
фигура), отражаясь
в
плоскости
как в
«двухстороннем зеркале», совме-
щается
с
левой
ее
частью (фигурой).
В
результате этот элемент симме-
трии связывает энантиоморфные фигуры,
т. е.
какую-либо фигуру
(или
ее часть)
с ее
зеркальным отражением (рис.
2.26; 2.3в и
2.6я).
В
симво-
лике Браве зеркальная плоскость симметрии
(и
операция отражения
в
плоскости) обозначается буквой
Р,
графически — двойной
(или
иногда
жирной) линией.
Энантиоморфные фигуры могут быть связаны
и
другим элементом
симметрии
—
центром инверсии (или точкой симметрии),
как бы
«зер-
кальной точкой», «отражаясь» (инвертируясь)
в
которой правая фигура
не только переходит
в
левую,
по и как бы
переворачивается. Точка
ин-
версии
при
этом играет роль фокуса линзы фотоаппарата,
и
связанные
ею фигуры соотносятся
как
предмет
и его
изображение
на
фотопленке
(рис.
2.2е; 2.3г;
2.66).
Любой точке фигуры, обладающей центром инверсии, соответству-
ет эквивалентная точка
на
продолжении прямой, соединяющей первую
точку
с
центром,
при
этом расстояния
от
центра
до
обеих точек равны
между собой (рис.
2.66).
Поэтому каждой вершине цеитросимметричного
многогранника соответствует равноудаленная
от
центра (совпадающего
с центром тяжести этого многогранника) эквивалентная вершина, каж-
дому ребру
—
равноудаленное, равное, но противоположно направленное
(антипараллелыгое) ребро,
а
каждой грани
—
равноудаленная, равная,
но
антипараллельная грань (см. рис. 2.3г).
На
рис.
2.6
хорошо видно, что при
повороте нижней запятой
на
180° зеркальная плоскость, расположенная
б
а
Рис.
2.6.
Иллюстрация операций (элементов) симметрии
II
рода:
а —
отражения
в зеркальной плоскости симметрии, расположенной между фигурами:
б
—
инверсии
(«отражения»)
в
точке
С
— плоскость симметрии «свернулась»
в
точку

Глава 2. Симметрия кристаллов
55
между параллельными фигурами (рис. 2.6а), как бы «свертывается»
в «зеркальную» точку, сами же фигуры при этом становятся антипарал-
лельными.
Обозначается центр инверсии в символике Браве буквой С(фр.
centre
—
центр), графически
—
точкой, маленьким кружком (о) или также буквой
С. Для обозначения операции инверсии в точке служит буква i (от фр.
inverse
— обратный).
Рассмотренные выше элементы симметрии — поворотные оси, зер-
кальная плоскость и центр инверсии — часто называют простыми, так
как каждый из них задает лишь одну симметрическую операцию: пово-
рот, отражение или инверсию в точке соответственно. Для описания же
симметрии некоторых кристаллов простых элементов симметрии оказы-
вается явно недостаточно, так как в них могут присутствовать сложные
элементы симметрии, позволяющие совмещать равные фигуры (или их
части) путем двойной операции — поворота (операции I рода) и отраже-
ния (операции II рода).
Если поворот вокруг некоторой оси сопровождается отражением
в перпендикулярной к ней плоскости, то такую сложную ось называют
зеркально-поворотной (или просто зеркальной) осью симметрии. Если
же за поворотом следует отражение в точке симметрии, расположенной
на этой оси, т. е. инверсия, то такую, тоже сложную, ось называют инвер-
сионной.
В общем случае каждое из совместных действий
—
поворот и отраже-
ние — мнимое (рис. 2.7 и 2.8). Поэтому и последовательность, в которой
проводятся эти операции, безразлична; иными словами, операции ком-
мутируют.
В символике Браве зеркальные оси обозначаются £ , инверсион-
ные
—
£ .
Рассмотрев действия сложных осей симметрии всех кристаллографи-
ческих порядков, убеждаемся в том, что не все из них оказываются ориги-
нальными. Так, в сложных осях 1-го порядка (£ и £,) поворотная ком-
понента равна нулю, поэтому вторая операция симметрии — отражение
в точке или плоскости — оказывается единственной и не мнимой, а дейст-
вительной. Таким образом, действие инверсионной оси 1-го порядка анало-
гично действию простого элемента симметрии
—
центра инверсии
—
£, = С,
так же как действие зеркальной оси 1-го порядка можно заменить отра-
жением в зеркальной плоскости, перпендикулярной этой оси, — £, = Р
(т. е. L
х
— это нормаль к Р). Действие сложных осей 2-го порядка £
2
и £
2
также можно заменить действием простых симметрических операций
—
отражением в реальной плоскости симметрии Р, перпендикулярной оси,
или инверсией в точке С соответственно. Обратившись к рис. 2.8, видим,
что две мнимые операции — отражение в плоскости и поворот на 180°
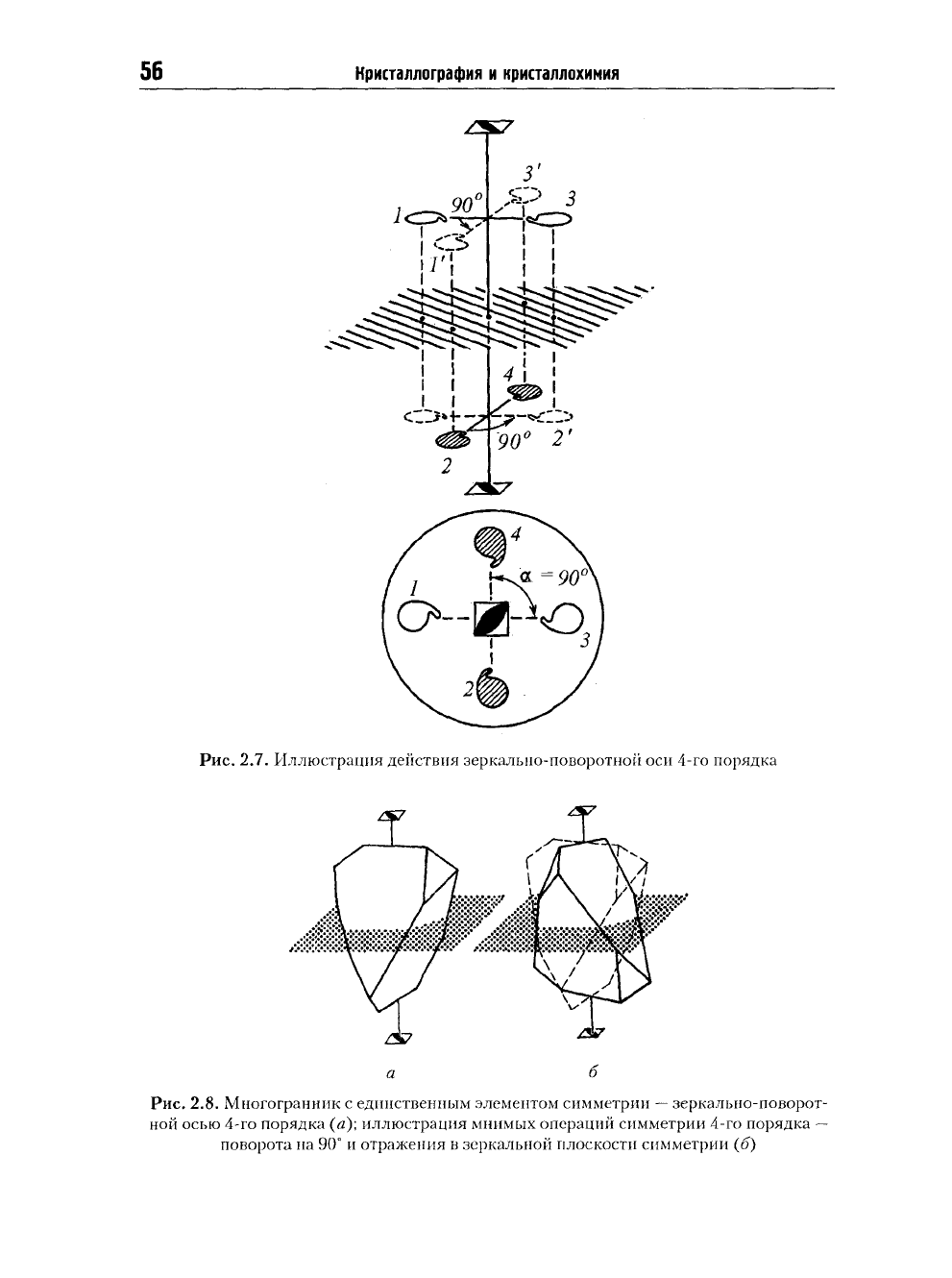
56
Кристаллография и кристаллохимия
Рис.
2.8. Многогранник с единственным элементом симметрии
—
зеркально-поворот-
ной осью 4-го порядка (в); иллюстрация мнимых операций симметрии 4-го порядка
—
поворота на 90° и отражения в зеркальной плоскости симметрии (б)

Глава
2.
Симметрия кристаллов
57
вокруг
оси 2-го
порядка — эквивалентны отражению
в
точке симметрии
(инверсии
в
точке),
а
мнимый поворот
на
180°, сопровождаемый мнимым
отражением
в
точке симметрии, можно заменить отражением
в
реальной
плоскости симметрии, перпендикулярной этой
оси.
Отсюда убеждаемся
в
том, что
действие инверсионной
оси £
аналогично действию зеркаль-
но-поворотной
оси £
2
, так же как
действие
оси £
(
можно заменить дей-
ствием
оси £,, т. е. £, = £
2
= С, £, = £
2
= Р.
Размножив асимметричную фигурку (запятую) сложными осями
3-
го
и 6-го
порядков
(рис. 2.9),
нетрудно убедиться
в том, что и они не
являются оригинальными,
т. е. их
действия можно представить сочета-
ниями простых действительных операций
(и,
соответственно, элемен-
тов) симметрии:
l,=l
6
=L
3
P,
где
Р
_L
L
v
и
(где
С
расположен
на оси 3-го
порядка). Оригинальной (незаменимой
простыми элементами симметрии) оказывается
в
кристаллах лишь
ось
4-
го порядка
(см. рис. 2.7),
причем результат действия инверсионной
и
зеркально-поворотной осей
4-го
порядка одинаков,
т. е. £
4
= £
4
,
поэтому
лишь
эти оси
имеют свое графическое обозначение
—
Й5
!
.
Проанализировав действия зеркально-поворотных
и
инверсионных
осей кристаллографических порядков, убеждаемся
в том, что
каждой
зеркально-поворотной
оси
можно поставить
в
соответствие действие
со-
ответствующей инверсионной
оси
симметрии:
£
]
— £
2
» £
2
i^y & з ^(i* ^
в
f*3> ,\ i^?c
Лишь
в
случае
со
сложными осями
4-го
порядка результат будет одним
и
тем же, но
последовательность получения точек будет иная. Представ-
ляя
в
общем виде действия зеркально-поворотной
и
инверсионной осей,
можно продемонстрировать
на рис. 2.10, что
операция каждой зеркаль-
ной
оси с
элементарным углом поворота
а
может быть заменена опера-
цией инверсионной
оси с
элементарным углом поворота
а' = 180° - а:
1
В
кристаллографической литературе
для
инверсионных осей
6-го
порядка
часто используется знак
А<
Однако, поскольку
£ = ^ jP
x
>
т
-
е
-
ось
можно
за-
менить реальными
(а не
мнимыми) элементами симметрии
—
поворотной осью
3-го порядка
и
перпендикулярной
к ней
зеркальной плоскостью, имеющими
свои условные обозначения
на
графиках, этот значок
нет
смысла использовать,
так
как он
фактически дублирует
их
обозначения.
58
Кристаллография
и
кристаллохимия
а
б
Рис.
2.9.
Иллюстрация замены некоторых сложных осей простыми элементами
симметрии:
а — £
(
. = / = L
:i
C\ б
—
£ = f
=
L,P
&
::
j->*r
=
f~X ; (2.2.1)
"
а " 180°-а
поэтому
при
описании симметрии кристаллов пользуются каким-либо
одним видом осей: простыми либо сложными
—
инверсионными
или
зеркальными:
L.^L,3PC
= f.
3
ЗЦЗР
- £(.
31,ЗР,
Р^ЗР'Р"
= /,6 з/,ЗР = /.'.,
3I..3P,
i.^L;iP
=
l
A
2L
2
2P
x
.
Обратим внимание
на то, что,
записав
в
символе сложную
ось,
заме-
няющие
ее
простые элементы симметрии
уже не
учитывают.
Для осей некристаллографических порядков
в
приведенную форму-
лу
(2.2.1)
вводится коэффициент
q —
наименьшее целое число, приво-
дящее
к
целочисленному значению
п'\
f
:м>о°
—
f ,
жо°
'
- п= ' -
И
=
./1
а
\ЫГ-а
1
Обратим внимание
на то, что при
записи комплекса элементов симметрии
кристалла
(группы симметрии,
см.
параграф
2.5)
сначала фиксируются
оси
выс-
ших
порядков, далее
—
плоскости симметрии
и
центр инверсии (например,
3L/iL.fiL,9PC,
LfiLJPC).

Глава
2.
Симметрия кристаллов
59
j
9-
/
7SO*-a
I \
Рис.
2.10.
Зависимость между зеркальным (угол поворота
а) и
инверсионным
(угол поворота
а = 180° - а)
поворотами
Записывая
в
виде формулы комплекс элементов симметрии кристал-
ла, одноименные элементы симметрии
(оси
одинаковых порядков
или
плоскости симметрии) объединяют коэффициентами (например:
31
2
,
6Р
и т. д.).
Однако целесообразно различать неэквивалентные
и
эквива-
лентные одноименные элементы симметрии, понимая
под
последними
элементы, связанные какими-либо операциями симметрии данного кри-
сталла,
и
группируя
их
посредством соответствующих коэффициентов.
Например, вместо
L.
2
2P
можно записать L.
2
FF', вместо L
A
AP — L^2F2F'.
Без изменений остается лишь запись £
3
ЗР,
где все
плоскости симметрии
оказываются эквивалентными,
т. е.
связанными поворотами
на 120°
вокруг
оси 3-го
порядка (рис.
2.11).
2.3. МЕТОДЫ ПРОЕЦИРОВАНИЯ КРИСТАЛЛОВ
Рассмотрим
в
качестве примера (рис.
2.12)
многогранник
в
виде кир-
пича
(а) и
кристалл серы
(б),
обладающие одинаковым набором элемен-
тов симметрии — 3Z
2
3PC
=
L,'L"L
2
"PF'F"
С. Их
различие заключается
в количестве
и
расположении граней относительно указанных элемен-
тов симметрии. Поэтому
для
того, чтобы получить полную информацию
об огранке кристалла, необходимо
не
только найти
и
зафиксировать
в
пространстве элементы
его
симметрии,
но и,
используя основной закон
постоянства углов, зафиксировать грани данного кристалла относитель-
но
его
элементов симметрии. Наибольшее распространение
в
кристал-
лографической практике получили сферическая, стереографическая
и
гномостереографическая проекции кристаллов. Познакомимся подроб-
нее
с
сущностью построения указанных проекций.
2.3.1.
Сферические проекции
Главное достоинство метода сферических проекций
—
метода изо-
бражения элементов симметрии,
а
также граней
и
ребер кристаллов
—
