Егоров-Тисменко Ю.К. Кристаллография и кристаллохимия

Подождите немного. Документ загружается.

300

Кристаллография и кристаллохимия

Точки, не лежащие на макроэлементах симметрии, подвержены всем

симметрическим операциям пространственной группы и образуют об-

щую правильную систему (симметрия позиции 1) (все остальные

—

частные).

Симметрия позиции правильной системы точек определяет и другие

ее характеристики: величину симметрии, число степеней свободы, крат-

ность и координаты точек.

Величина симметрии определяется числом точек, на которые раз-

делится одна точка, выведенная из данной частной позиции в общую,

т. с. соответствует порядку той точечной группы, которая характеризует

симметрию позиции.

Число степеней свободы зависит от элементов симметрии, фикси-

рующих данную позицию (точку). Точка общего положения

—

тривари-

антна, т. е. не фиксирована пи одним элементом симметрии и, следова-

тельно, имеет три степени свободы. Точка, расположенная на зеркальной

плоскости, — дивариантна, с двумя степенями свободы. Точка на пово-

ротной оси симметрии — моновариантна, с одной степенью свободы.

Позиция, совпадающая с центром инверсии, точкой пересечения осей

симметрии или с особой точкой инверсионной оси,

—

инвариантна (ион-

вариантна), т. е. строго фиксирована этими элементами симметрии и ли-

шена степеней свободы.

Еще одной характеристикой правильных систем точек служит ее

кратность, т. е. число точек, приходящихся на одну элементарную ячейку.

Кратность любой правильной системы зависит от величины симметрии

позиций ее точек. И чем более симметрична позиция (т. е. чем больше

ее величина симметрии), тем меньше ее кратность, определяемая как

частное от деления порядка данной пространственной группы на величи-

ну симметрии позиции. Очевидна и обратная зависимость: произведение

кратности правильной системы точек (я.) на ее величину симметрии (s)

постоянно и равно кратности общей правильной системы (п), т. е. по-

рядку пространственной группы: п = п.- s

Данная зависимость помогает

получить недостающие сведения о той или иной кристаллической струк-

туре

—

информацию о расположении в ней атомов или молекул.

Число степеней свободы правильных систем точек отражено в зна-

чениях их координат. При этом координаты точек без степеней свободы

обозначаются рациональными долями параметров элементарной ячейки,

тогда как координаты точек со степенями свободы

—

нефиксированными

значениями х,уиг. Именно изменение последних приводит к различным

значениям координационных чисел (см. параграф 6.3), а следовательно,

и к переходу от одного структурного типа к другому.

В пространственной группе Рта2 (рис. 6.29) принципиально раз-

ными оказываются лишь три правильные системы точек: общая

—

три-

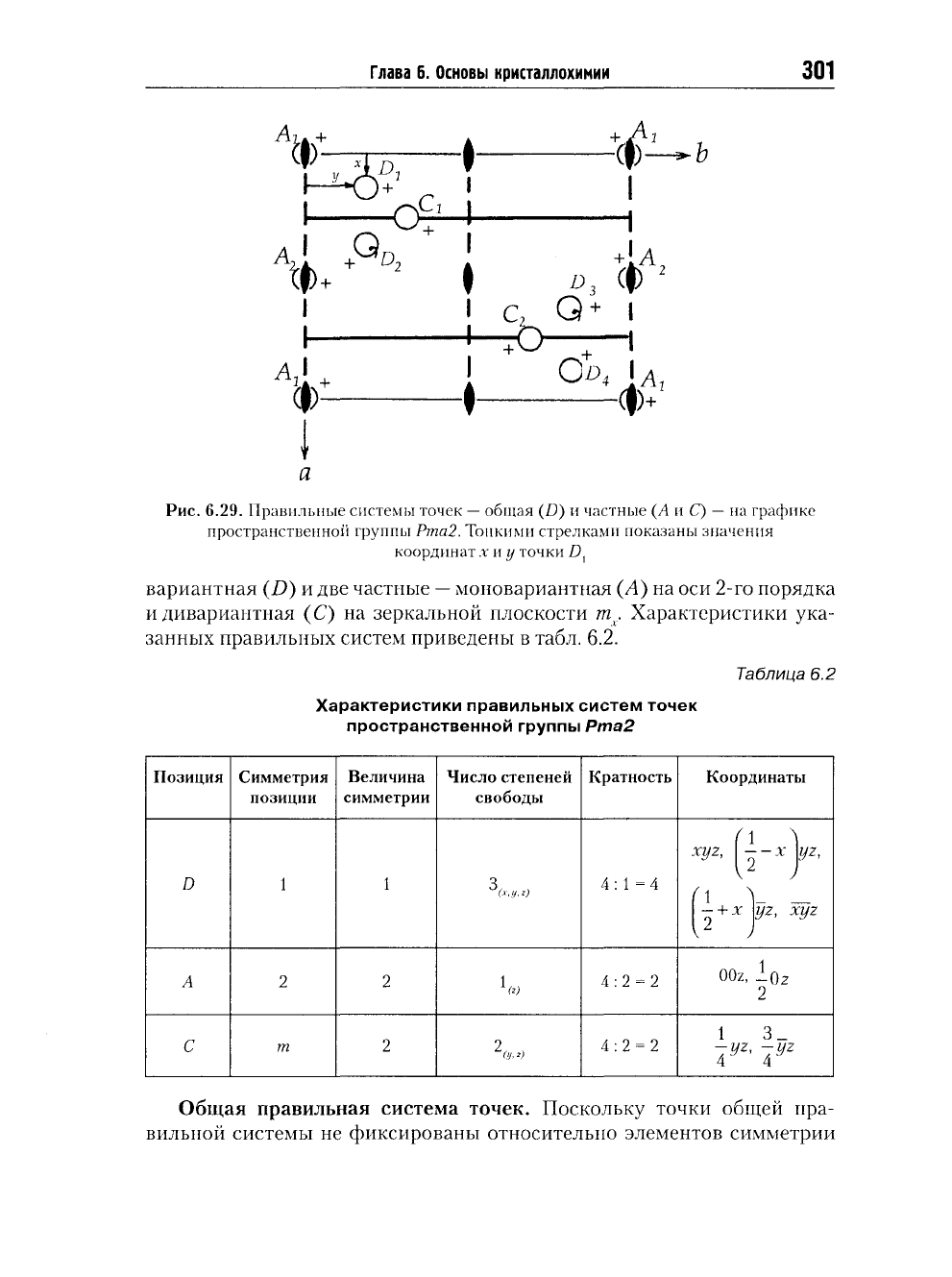
Глава 6. Основы кристаллохимии

301

Рис.

6.29. Правильные системы точек

—

общая (D) и частные (А и С) — на графике

пространственной группы Рта2. Топкими стрелками показаны значения

координат х и у точки D

вариантная (D) и две частные

—

моновариантная (А) на оси 2-го порядка

и дивариантная (С) на зеркальной плоскости т

. Характеристики ука-

занных правильных систем приведены в табл. 6.2.

Таблица 6.2

Характеристики правильных систем точек

пространственной группы

Рта2

Позиция Симметрия

позиции

Величина

симметрии

Число степеней

свободы

Кратность Координаты

1 4:1=4

xyz, — х yz,

fl V -

—

+ x yz, xyz

)

А 2 2 4:2 = 2

OOz,

i02

т 2

(!/,')

4:2 = 2

1 3_

-yz, -yz

4 4

Общая правильная система точек. Поскольку точки общей пра-

вильной системы не фиксированы относительно элементов симметрии

302

Кристаллография

кристаллохимия

данной пространственной группы

и,

следовательно, имеют

три

степени

свободы вдоль трех координатных направлений,

то

любое изменение

их координат

не

приводит

изменению кратности данной системы

то-

чек. Каждая координата, выраженная

долях элементарной ячейки,

от-

кладывается (измеряется)

от

начала координат вдоль соответствующей

координатной

оси.

Координата

±z

показывает высоту точки

над (под)

нулевым уровнем (плоскостью чертежа). Однако

на

графике

(рис.

6.29)

рядом

точкой оставляется лишь знак этой координаты

(+ или -), ибо

абсолютного значения вертикальной координаты

проекции простран-

ственной группы

па

плоскость чертежа

не

видно.

Для получения всех точек общей правильной системы следует

по-

действовать подрешеточными

—

порождающими

—

элементами симме-

трии группы.

На

заключительном этапе получения всех точек системы

необходимо включить

действие трансляционный комплекс данной

группы симметрии.

При

этом

непримитивных решетках число точек

правильной системы увеличится

по

сравнению

примитивной

соот-

ветствии

числом дополнительных трансляционных векторов:

в С-, I-

ячейках —

в два

раза,

Л-ячейке —

в три

раза

и в

F-ячейке —

четыре

раза.

На графике гемиморфной пространственной группы Рта2

для по-

лучения всех точек общего положения

(а их

количество (кратность)

Р-решетке соответствует порядку точечной группы тгп2, равному

(см.

рис.

6.30)

достаточно последовательно подействовать

на

исходную

точку

координатами

xyz

независимыми плоскостями симметрии

(т

а),

обозначенными

символе данной пространственной группы, посчи-

тав

их

порождающими элементами симметрии. Порожденные

же

этими

плоскостями

оси 2-го

порядка можно использовать

для

проверки пра-

вильности полученного результата.

Итак, исходная точка

(см. рис.

6.29) с

координатами

xyz

после

от-

ражения

зеркальной плоскости

займет энантиоморфное положение

(\ \

координатами

—х yz (на

графике такую энантиоморфную точку

„Л

;

отмечают запятой):

xyz(D

)-m

--х yz (D

)

Дальнейшее отражение полученных двух точек

плоскости

пере-

ведет каждую

из них в

энантиоморфное положение:

xyz(D

)-a

у,

г (£>),

—

wz (DJ

•

—>

x,y,z (D

)

(точка

при

этом потеряет запятую).

Глава

Основы кристаллохимии

303

Последовательные отражения исходной точки

двух взаимно пер-

пендикулярных плоскостях симметрии

и а

равносильны повороту

вокруг результирующей

оси 2 .

Действительно, каждая пара конгруэнт-

ных точек

— D

и D

, D

и D —

связана поворотом вокруг

оси 2,

располо-

„11

женпой

позиции

--г .

Частные правильные системы точек. Моновариантная позиция

(Л)

в данной группе расположена

на

поворотной

оси

симметрии

имеет

одну степень свободы вдоль координатной

оси Z.

Поэтому соответству-

ющая

оси Z

координата

(+г),

будучи переменной величиной,

на

графике

будет обозначена знаком

«+» (см. рис.

6.29).

Две

другие

ее

координаты

строго зафиксированы осью

2,.

Таким образом, координаты исходной

точки

Л — OOz.

Вторую точку

(Л

)

можно получить, подействовав

на нее

либо плоскостью

т.,

либо плоскостью

а . В

результате получим точку

1 "

с координатами

00*

ел,;-и-*

^ог

(л

Величина симметрии единственной

пространственной группе

Рта2 дивариантной позиции

(С) —

позиции

на

зеркальной плоскости

т (рис. 6.29) с

двумя степенями свободы

—-

равна

2, что

уменьшает

ее

кратность вдвое

по

сравнению

кратностью общей правильной системы

(4:2 = 2).

Поскольку плоскость

перпендикулярна

оси X, то

располо-

женная

на ней

исходная точка имеет

две

переменные координаты вдоль

двух координатных осей

— в

данном случае

Г и Z: ^yz.

Точка

такими

координатами плоскостью

т не

размножается

— на нее

действует лишь

независимая

от

плоскости

плоскость

а :

1 3 _

-yz(С,)

a -^-yz(C

4 4

Как легко убедиться, координаты точек легко получить, используя

график соответствующей пространственной группы. Однако, зная законо-

мерности изменения координат точек

под

действием того

или

иного эле-

мента симметрии

(см.

параграф

2.4.2),

можно

их

рассчитать

аналитиче-

ски.

Это не

вызывает затруднений, если данный размножающий элемент

симметрии проходит через начало координат. Например, плоскость сим-

метрии

переведет точку

xyz в

положение

xyz и т. д.

Если же размножа-

ющий элемент симметрии

не

проходит через начало координат,

то,

прежде

чем действовать

на

какую-либо точку этим элементом симметрии, надо

временно изменить начало координат, перенеся

его на

этот элемент,

и за-

писать координаты точки относительно выбранного нового начала. Затем

304

Кристаллография

кристаллохимия

произвести заданную элементом симметрическую операцию

и уже

после

этого координаты получе^той точки пересчитать

старому началу

ко-

ординат.

В Интернациональных таблицах

характеристику каждой правиль-

ной системы точек пространственной группы помимо кратности (коли-

чества позиций

элементарной ячейке)

и ее

симметрии входит буквен-

ное обозначение Уайкоффа

(Wyckoff)

(последовательность латинского

алфавита отвечает увеличению кратности позиции). Самая симметрич-

ная позиция

—

позиция

минимальной кратностью

—

обозначается

буквой

а.

Кроме этого, обязательно указывается символ данной про-

странственной группы

обозначении Шенфлиса,

ее

порядковый номер

и соответствующая точечная группа симметрии. Таким образом,

сим-

воле Уайкоффа независимые позиции даже

одинаковыми характери-

стиками, различающиеся лишь координатами, обозначаются разными

буквами.

В пространственной группе Рта2

= С

2т

позиция

на

оси

символе

Уайкоффа обозначается буквой

а, на оси -2

—

Ь, на

плоскости

—

с,

общего положения

—

(рис.

6.29).

Характеристика правильных систем точек

Интернациональных

та-

блицах выглядит следующим образом (рис.

6.30).

Positions

Coordinates

Multiplicity,

Wyckoff

letter.

Sire

symmetry

d 1

(l)x,y,z

(2)

x,y,z

(3)

x+Vi,

(4) x +

Л,

y, z

с m..

Й,

y.z

b ..2

Vl,

Vi,

Уг,

a ..2

0,2

'/2,0,2

Рис.

6.30.

Характеристика правильных систем точек

Интернациональных таблицах

6.3. КООРДИНАЦИОННЫЕ ЧИСЛА, КООРДИНАЦИОННЫЕ ПОЛИЭДРЫ,

ЧИСЛО ФОРМУЛЬНЫХ ЕДИНИЦ

Зная модель кристаллической структуры,

т.

е.

пространственное рас-

положение атомов относительно элементов симметрии

элементарной

ячейке —

их

координаты,

следовательно,

характеристики правильных

систем точек, которые занимают атомы, можно сделать

ряд

кристаллохи-

мических выводов, используя достаточно простые приемы описания струк-

тур.

Поскольку

выведенных выше решеток Браве

не

могут отразить

все

Глава

Основы кристаллохимии

305

многообразие известных

настоящему времени кристаллических струк-

тур,

необходимы характеристики, позволяющие однозначно описать

ин-

дивидуальные особенности каждой кристаллической структуры.

таким

характеристикам, дающим представление

геометрическом характере

структуры, относятся: координационные числа

(КЧ),

координационные

многогранники (КМ),

или

полиэдры (КП),

число формульных единиц

(Z).

Прежде всего

по

модели можно решить вопрос

типе химической

формулы рассматриваемого соединения,

т. е.

установить количественное

соотношение атомов

структуре.

Это

нетрудно сделать

на

основе ана-

лиза взаимного окружения — взаимной координации — атомов разных

(или одинаковых) элементов.

6.3.1.

Координационное число

(КЧ)

Термин «координация атома»

был

введен

химии

конце

XIX в.

в процессе формирования

ее

новой области — химии координационных

(комплексных) соединений.

И уже в 1893

г.

А.

Вернер ввел понятие коор-

динационное число

(КЧ) как

число атомов (лигандов

), непосредствен-

но связанных

центральным. Химики

свое время столкнулись

с тем

фактом,

что

число связей, образуемых атомом, может отличаться

от его

формальной валентности

даже превышать

ее.

Например,

ионном

со-

единении

NaCl

каждый

ион

окружен шестью ионами противоположного

заряда (КЧ

№/С]

= 6,

c|/Na

= 6),

хотя формальная валентность атомов

Na и

С1 равна

Таким образом, согласно современному представлению,

КЧ

—

это число ближайших

данному атому (иону) соседних атомов (ионов)

структуре кристалла независимо

от

того, являются

они

атомами того

же сорта,

что и

центральный,

или

иного.

При

этом межатомные расстоя-

ния являются основным критерием, используемым

при

подсчете

КЧ.

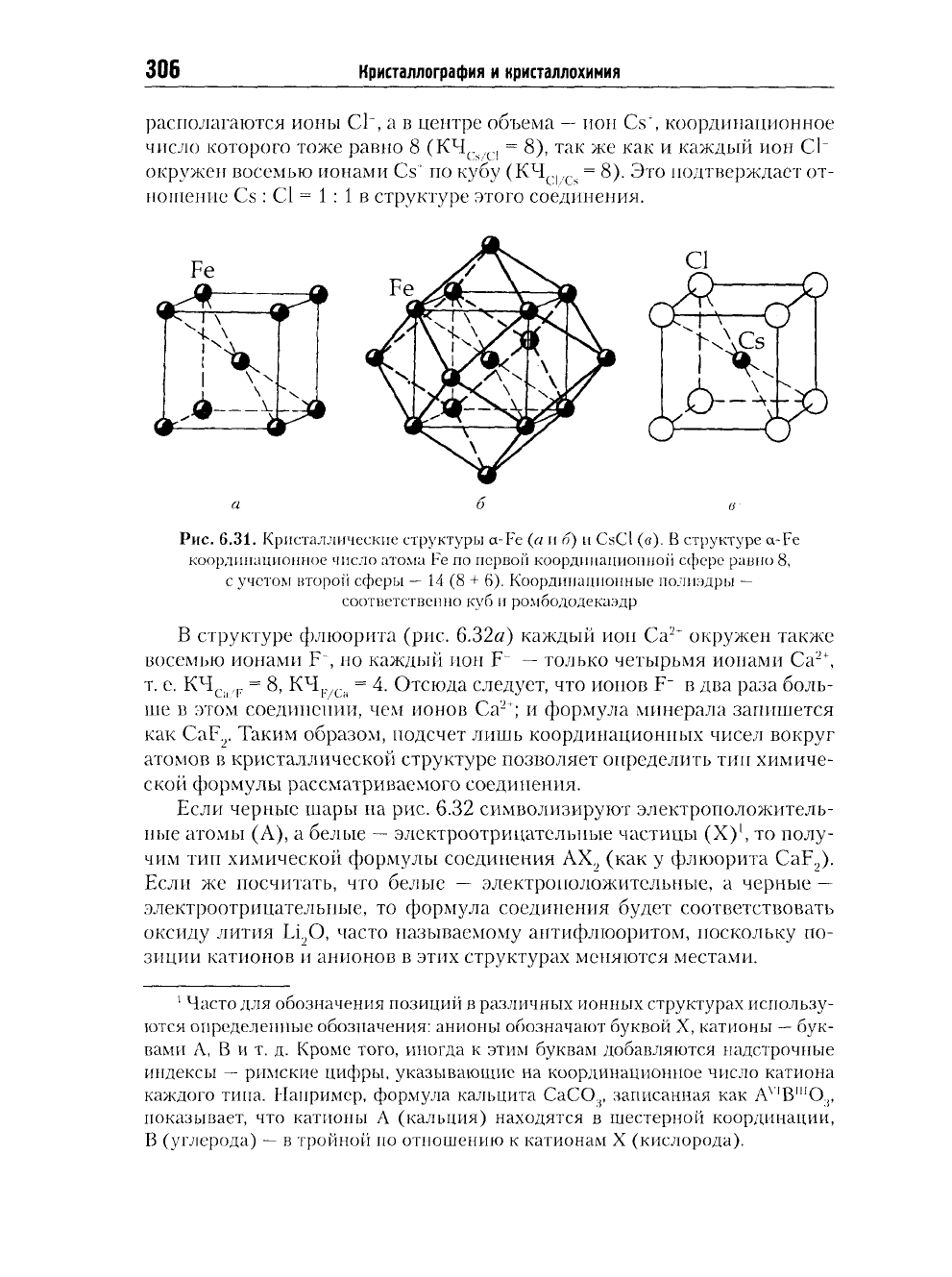
Например,

кубических структурах модификации

a-Fe (рис.

6.31я)

CsCl

(рис. 6.31в) координационные числа всех атомов равны

8: в

струк-

туре

a-Fe

атомы

располагаются

узлах объемноцентрированного куба,

отсюда КЧ

[;с/1

= 8

; в

структуре

CsCl

вершинах элементарной ячейки

Лиганд

(от

лат.

ligo

—

связываю) —

ион,

непосредственно связанный

цен-

тральным атомом (катионом).

Иногда, говоря

координационном числе,

не

ограничиваются лишь пер-

вой координационной сферой,

учитывают

вторую, третью

и т. д.

Например,

в случае структуры

a-Fe (или W) КЧ,.

можно увеличить

до 14 (8 + 6) за

счет

шести атомов второй координационной сферы, расположенных

центрах сосед-

них элементарных ячеек

удаленных

от

центрального

на

расстояния, превыша-

ющие расстояния

до

атомов первой координационной сферы

на 15%. С

учетом

атомов второй сферы координационный полиэдр будет иметь форму ромбодо-

декаэдра

(рис. 6.316). В

этом случае полезно указать

не

только

КЧ, но и

рассто-

яния

до

атомов вовлекаемых координационных сфер.

306

Кристаллография и кристаллохимия

располагаются ионы СТ, а в центре объема

—

ион Cs", координационное

число которого тоже равно 8 (КЧ

, = 8), так же как и каждый ион СТ

окружен восемью ионами Cs" по кубу (КЧ

С|/С

. = 8). Это подтверждает от-

ношение Cs: Cl = 1 : 1 в структуре этого соединения.

а б в

Рис.

6.31. Кристаллические структуры a-Fe (я и б) и

CsCl

(в). В структуре a-Fe

координационное число атома Fe по первой координационной сфере равно 8,

с учетом второй сферы — 14 (8 + 6). Координационные полиэдры —

соответственно куб и ромбододекаэдр

В структуре флюорита (рис. 6.32а) каждый ион Са

* окружен также

восемью ионами F", но каждый ион F

— только четырьмя ионами Са

т. е. КЧ

.,|

= 8, КЧ,,

/Са

= 4. Отсюда следует, что ионов F" в два раза боль-

ше в этом соединении, чем ионов Са

; и формула минерала запишется

как CaF

. Таким образом, подсчет лишь координационных чисел вокруг

атомов в кристаллической структуре позволяет определить тип химиче-

ской формулы рассматриваемого соединения.

Если черные шары на рис. 6.32 символизируют электроположитель-

ные атомы (А), а белые — электроотрицательные частицы (X)', то полу-

чим тип химической формулы соединения АХ., (как у флюорита CaF.,).

Если же посчитать, что белые — электроположительные, а черные

—

электроотрицательные, то формула соединения будет соответствовать

оксиду лития

Li.,0,

часто называемому антифлюоритом, поскольку по-

зиции катионов и анионов в этих структурах меняются местами.

Часто для обозначения позиций в различных ионных структурах использу-

ются определенные обозначения: анионы обозначают буквой X, катионы — бук-

вами Л, В и т. д. Кроме того, иногда к этим буквам добавляются надстрочные

индексы — римские цифры, указывающие на координационное число катиона

каждого типа. Например, формула кальцита СаСО , записанная как А

У|

показывает, что катионы А (кальция) находятся в шестерной координации,

В (углерода) — в тройной по отношению к катионам X (кислорода).

Глава 6. Основы кристаллохимии

307

Следует отмстить, что критерий минимальности межатомного рас-

стояния при определении координационного числа не является абсолют-

ным и может быть применен далеко не во всех случаях. Во-первых, свя-

зи центрального атома с атомами координационной сферы могут иметь

различную прочность и даже различную природу. Например, в графите

расстояния до трех атомов С в слое (см. рис. 6.40 в параграфе 6.5) состав-

ляет 1,42 А, расстояние же до четвертого атома из соседнего слоя боль-

ше 3 А. Во-вторых, атомы, входящие в окружение центрального, могут

иметь различную химическую природу. Следовательно, и расстояния

до них будут различны, даже если прочность связей будет одинакова.

В-третьих, даже если в окружение входят атомы одного сорта, они могут

располагаться на разных расстояниях от центрального. В этом случае в

координационную сферу включают атомы, расположенные на расстоя-

ниях, заключенных в определенном интервале. Например, в структуре

гипса CaSO,, • 2Н

0 КЧ

= 8; при этом расстояния Са-О изменяются

в диапазоне от 2,37 до 2,55 А. Соответственно должна меняться и проч-

ность химических связей.

Рис.

6.32. Кристаллическая структура флюорита CaF, (= антифлюорита

0).

Общий

вид структуры (а) с выделенными координационными полиэдрами вокруг атомов

Са (О) и F (Li) и план структуры с началом координат в атоме Са (б) и в атоме F (о).

Сдвиг контура элементарной ячейки легко выявляет количество принадлежащих

ей атомов Са и F

6.3.2.

Координационные полиэдры (КП)

Для полного описания особенностей кристаллических структур,

а, точнее, для получения характеристики особенностей ближайшего ок-

ружения каждого атома, кроме количественной оценки (т. е. КЧ) необ-

ходимо охарактеризовать и геометрию расположения лигандов вокруг

центрального атома (иона), т. е. дать характеристику координационного

полиэдра (КП) (многогранника — КМ), в вершинах которого располага-

ются лиганды.

308

Кристаллография и кристаллохимия

Например, в структуре флюорита CaF

(см. рис. 6.32 а) координа-

ционный полиэдр (КП) вокруг иона Са

будет иметь форму куба, в вер-

шинах которого располагаются центры тяжести ионов F". КП вокруг

ионов F~ будет иметь форму тетраэдра, в вершинах которого располо-

жены центры тяжести ионов Са

. Такая дополнительная характеристи-

ка необходима хотя бы потому, что одному и тому же координационному

числу могут отвечать разные координационные полиэдры. Например,

в структуре куперита PtS (рис. 6.33) координационные числа для ато-

мов Pt и S одинаковы:

PtS

= 4 и K4

S [ч

= 4. Однако их координаци-

онные полиэдры различны: КП для атомов Pt — квадрат, а для атомов

—

тетраэдр.

Рис.

6.33. Кристаллическая структура куперита PtS: КЧ,

= 4, КЧ ,

= 4.

Координационные многогранники — разные: квадрат

—

для атомов Pt,

тетраэдр

—

для атомов S

В высокосимметричных и не очень сложных кристаллических струк-

турах ближайшие соседи располагаются на одинаковых расстояниях от

центрального атома, и координационные полиэдры в этом случае обла-

дают достаточно высокой симметрией. В низкосимметричных структу-

рах к одной и той же координационной сфере обычно относят атомы, на-

ходящиеся лишь на приблизительно равных расстояниях, в этих случаях

координационные полиэдры не имеют правильной высокосимметрич-

ной формы (рис.

6.34).

Координационные числа и координационные многогранники явля-

ются важнейшими характеристиками конкретной кристаллической

структуры, отличающими ее от остальных структур. На этой основе

можно проводить классификацию, относя конкретную кристаллическую

структуру к определенному структурному типу.

Глава 6. Основы кристаллохимии

309

Ж 3 и к

Рис.

6.34. Некоторые координационные полиэдры, встречающиеся в кристаллических

структурах: а — гантель (КЧ = 2); б — треугольник (КЧ = 3); в — квадрат (КЧ = 4);

г — тетраэдр (КЧ = 4); д — тригональная призма (КЧ = 6); е

—

октаэдр (КЧ = 6);

ж — куб (КЧ = 8); з

—

томсоновский куб (КЧ = 8); и

—

архимедов

кубооктаэдр (КЧ = 12); к — гексагональный аналог

кубооктаэдра (КЧ = 12)

6.3.3. Число формульных единиц (Z)

Установить тип химической формулы по структурным данным (т. е.

по модели структуры или по ее проекции

—

чертежу) можно и иным пу-

тем, подсчитав число атомов каждого сорта (химического элемента), при-

ходящихся на одну элементарную ячейку. В рассматриваемой структуре

флюорита CaF.

;

все восемь ионов F~ расположены внутри элементарной

ячейки, выделенной на рис.

6.326

штриховыми линиями, т. е. принад-

лежат только этой ячейке. Расположение же ионов Са

различно: часть

из них локализована в восьми вершинах кубической ячейки структуры

минерала, другая часть — в центрах всех шести ее граней. Поскольку

каждый из восьми «вершинных» ионов Са

принадлежит одновременно

восьми соседним элементарным ячейкам — кубам, то лишь

/ часть каж-

дого из них принадлежит исходной ячейке. Таким образом, вклад «вер-

шинных» атомов Са в исходную ячейку будет равен 1 Са (

х 8 = 1 Са).

Каждый же из шести атомов Са, расположенных в центрах граней ку-

бической ячейки, принадлежит одновременно двум соседним ячейкам.

Отсюда вклад шести центрирующих грани куба атомов Са будет равен

/, х 6 = 3 Са. В итоге на одну элементарную ячейку будет приходиться

1 + 3 = 4 атома Са. Проведенный подсчет показывает, что на одну ячейку

приходятся четыре атома Са и восемь атомов F. Это подтверждает тип

химической формулы (АХ

) минерала — CaF

, где атомов Са в два раза

меньше, чем атомов F. К аналогичным результатам легко прийти, если