Егоров-Тисменко Ю.К. Кристаллография и кристаллохимия

Подождите немного. Документ загружается.

290

Кристаллография

кристаллохимия

Обратим внимание

на то, что при

записи символов групп

стандарт-

ном аспекте отличающуюся от двух других плоскость принято располагать

перпендикулярно

оси

т. е.

фиксировать

на

третьей позиции символа.

Следующее семейство составят пространственные группы

двумя

плоскостями

т и (или) п и

одной плоскостью

горизонтальным сколь-

жением

(а или Ь) на

третьей позиции символа (поскольку вертикальное

скольжение

горизонтальной плоскости невозможно!):

Ртта

= Pmmb (D

) (рис.

6.21а);

Pnna=Pnnb

);

Ртпа

= Pnmb (Щ

);

Рпта

= Pmnb (D™) (рис. 6.216).

Как видим, каждая

из

двух первых групп имеет своего топологиче-

ского напарника. Однако стандартный аспект

Интернациональных

та-

блицах соответствует установке

плоскостью

а на

последнем месте сим-

вола.

Во

второй паре групп

(D'

и ОЦ)

вектор скольжения плоскости

а,

расположенный

пространственной группе Ртпа перпендикулярно пло-

скости

т и в

пространственной группе Рпта

—

перпендикулярно клино-

плоскости

(рис.

6.216"),

делает

эти

группы топологически разными.

В третьем семействе пространственных групп,

одной плоскостью

(или

п) на

последнем месте символа,

две

другие плоскости могут быть

либо однотипными,

т. с. обе с

вертикальным

или обе с

горизонтальным

скольжением:

Реет (D*), Рссп (DH),

Pbam (D

), Pban

(£>",,) (рис.

6.22a, б),

Pmma = Pmmb

Ртпа

ф Pnmb

Рис.

6.21.

Трансляционная компонента плоскости скользящего отражения третьей

позиции символа, параллельная одной

из

вертикальных зеркальных плоскостей

и перпендикулярная другой

(а),

делает

две

установки пространственной группы

2ll

топологически одинаковыми: Ртта

= Pmmb;

компонента, параллельная плоскости

(или

) и

перпендикулярная

(или и ), в

пространственных группах Ртпа

и Pmnb

соответственно

(б)

делает

эти

группы топологически различными,

т. е.

Ртпа

* Pmnb

Глава

Основы кристаллохимии

291

либо разного типа

—

одна

горизонтальным, другая

вертикальным сколь-

жением:

Pbcm(Dll),Pbcn(Dli).

В последнем, четвертом семействе пространственных групп

нет

пло-

скостей

тип. При

этом

одном варианте векторы скольжения двух

плоскостей параллельны друг другу

перпендикулярны вектору третьи

плоскости:

Рсса

(= Pbaa = Pbab = Pccb = Pbcb =

Рсаа)

= D*

(рис.

6.22А),

в другом

—

векторы скольжения плоскостей симметрии всех трех позиций

символа взаимно перпендикулярны

(со

скольжением вдоль осей

X, YnZ):

Pbca (=

Pcab)

= D'

(рис.

6.22г).

В итоге получены

пространственных групп ромбической голо-

эдрии

Р-решеткой.

Каждая пара плоскостей

символе ромбической голоэдрии задает

характер

положение результирующей

оси 2-го

порядка, расположен-

ной параллельно линии пересечения плоскостей

фиксированной

на не

занятой плоскостями позиции символа. Причем если

обе

порождающие

плоскости зеркальные

или обе

содержат параллельные трансляционные

векторы,

то

возникшая

ось

окажется поворотной. Если

же

вектор,

па-

раллельный

оси,

содержится лишь

одной

из

плоскостей,

он

поменяет

характер

оси на

винтовой. Таким образом, каждый символ ромбической

2 2 2

группы может быть записан

развернутом виде: Рттт

= Р ,

2 2 2 2 2 2 ттт

Ртпа

= Р—

'-,

Pbca

Р~—

—

Не

следует также забывать,

что

любая

п a b с а

пара элементов симметрии любой позиции развернутого символа

(ось 2-го

Реет

РЪат

Рсса

>*—

Pbca

Рис.

6.22.

Группы

однотипными вертикальными плоскостями: только

с вертикальными

(а, в) или

только

горизонтальным

(б)

скольжениями.

Трансляционные векторы всех трех плоскостей скользящего отражения

в пространственной группе

Pbca

направлены вдоль разных

координатных осей

(г)

10*

292

Кристаллография и кристаллохимия

порядка и перпендикулярная ей плоскость симметрии) обусловит появ-

ление центра инверсии.

Для вывода пространственных групп ромбической голоэдрии с осталь-

ными решетками Браве

—

С,

I, F— необходимо рассмотреть взаимодействие

дополнительных (некоординатных) векторов решетки с порождающими

плоскостями символа. В результате этого появятся дополнительные пло-

скости симметрии, чередующиеся на той или иной позиции символа с

исходными, либо плоскости, тождественно равные исходным, но другого

наименования.

Топологическая эквивалентность всех трех направлений ромбо-би-

пирамидального класса ттт делает центрировки А, В к С неразличи-

мыми. Однако центрировка одной пары граней элементарной ячейки

(например, центрировка грани С) делает горизонтальную плоскость то-

пологически отличной от двух других, в данном случае от вертикальных

плоскостей (первой и второй позиций символа), так как вектор Т

по-

разному ориентирован относительно горизонтальной и вертикальных

плоскостей (лежит в горизонтальной плоскости и расположен под ко-

сыми углами к вертикальным) и поэтому по-разному с ними взаимодей-

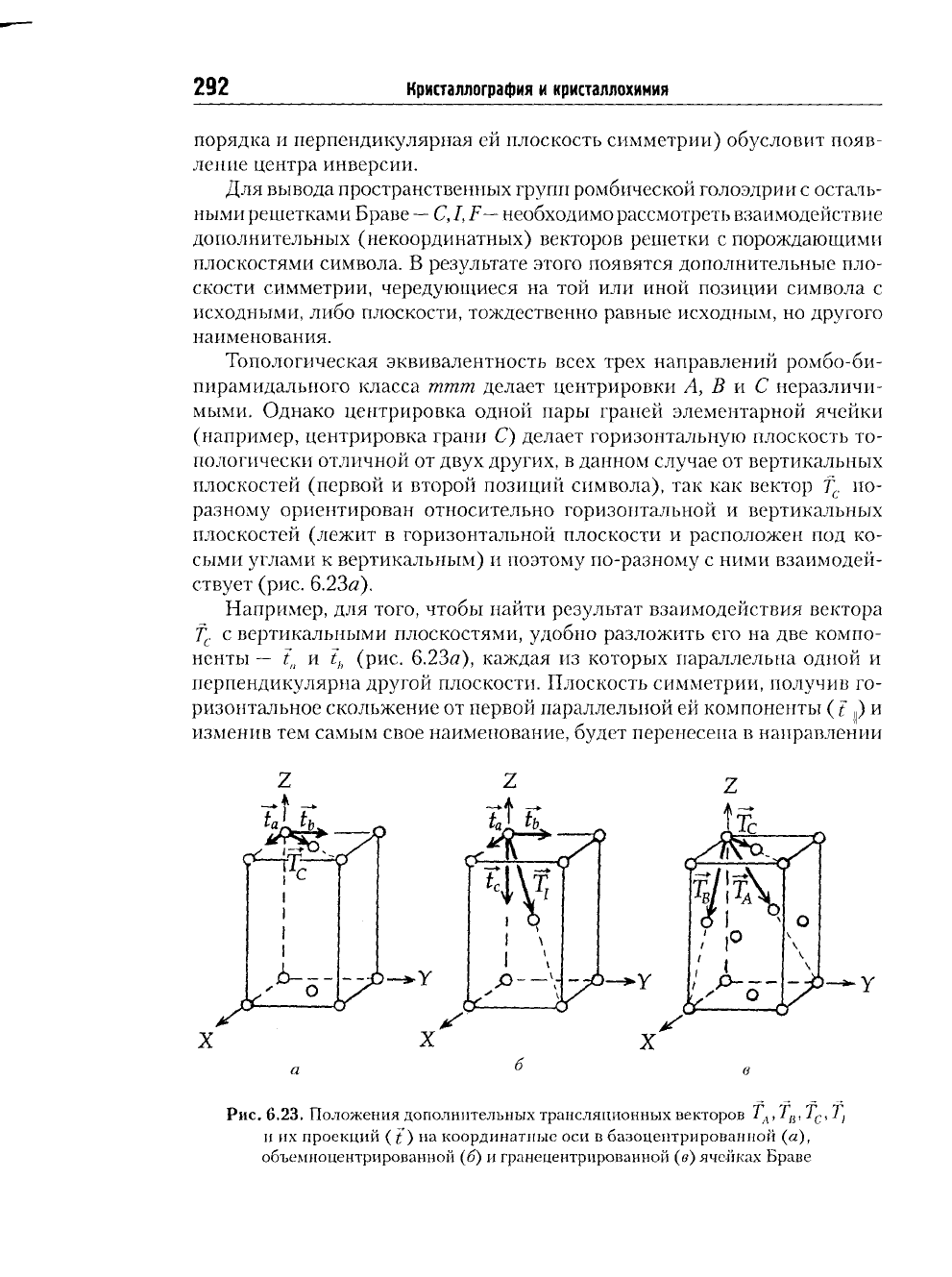
ствует (рис. 6.23а).

Например, для того, чтобы найти результат взаимодействия вектора

с вертикальными плоскостями, удобно разложить его на две компо-

ненты — t

и t

(рис. 6.23а), каждая из которых параллельна одной и

перпендикулярна другой плоскости. Плоскость симметрии, получив го-

ризонтальное скольжение от первой параллельной ей компоненты (t ц) и

изменив тем самым свое наименование, будет перенесена в направлении

XXX

Рис.

6.23. Положения дополнительных трансляционных векторов Т

, Т

, 7)

и их проекций ( {) на координатные оси в базоцентрированной (а),

объемноцентрированной (б) и гранецентрированной (в) ячейках Браве

Глава 6. Основы кристаллохимии

293

второй, перпендикулярной к ней компоненты (t

) на ее середину. Таким

образом, в базоцентрированной решетке (С) появятся дополнительные,

как бы «вложенные», плоскости симметрии, т. е. будет наблюдаться че-

редование плоскостей на первой и второй позициях: m(g)

и с(п).

Совсем иначе ведут себя горизонтальные плоскости (третья позиция

символа) т, п, а, Ь, взаимодействие которых с лежащим в них вектором

обусловит тождественное равенство плоскостей т = пка = Ь (где «=»

—

знак тождественности), т. е. одна и та же плоскость будет одновремен-

но «работать» в качестве плоскости как одного, так и другого наимено-

вания.

Таким образом, в базоцентрированных группах ромбической голо-

эдрии дополнительная трансляция f

обусловит следующие чередова-

ния плоскостей симметрии:

• на первой позиции символа

—

т(Ь) и с(п);

• на второй позиции символа

—

т(а) и с(п);

• на третьей позиции символа тождественное равенство т = пиа = Ь.

Это приведет к меньшему количеству пространственных групп с С-ре-

шеткой Браве.

Рассмотрев подобным образом взаимодействия плоскостей симмет-

рии с векторами объемноцентрированной и гранецентрированной ре-

шеток (рис.

6.236,

в), можно получить и соответствующие им простран-

ственные группы симметрии.

Принципы вычерчивания графиков

пространственных групп симметрии

Прежде чем задавать положения точек (атомов) относительно эле-

ментов симметрии кристаллической структуры, следует вычертить гра-

фик соответствующей пространственной группы.

Для этого, задав значения трансляционных координатных векто-

ров,

лежащих в плоскости чертежа, нужно изобразить в масштабе про-

екцию элементарной ячейки в соответствующей установке и далее при

вычерчивании гемиморфных (т. е. не имеющих горизонтальных элемен-

тов симметрии и центра инверсии) пространственных групп, посчитав

в качестве порождающих элементов симметрии записанные в символе

плоскости, изобразить их на соответствующих позициях. Если решетка

примитивная, то заданные плоскости симметрии будут взаимодейство-

вать лишь с перпендикулярными к ним координатными трансляционны-

ми векторами т,Т и j и между собой. В результате взаимодействия

Обозначение плоскости скользящего отражения буквой g не указывает на-

правление ее горизонтальной трансляционной составляющей. В скобки заключе-

ны дополнительные плоскости (например, g), чередующиеся с плоскостями т.

294

Кристаллография и кристаллохимия

плоскости с вектором, перпендикулярным к ней, возникнет плоскость

того же наименования на его середине.

Действительно, обратившись к рис. 6.24, которым проиллюстрирован

результат взаимодействия зеркальной плоскости симметрии с перпенди-

кулярной ей трансляцией, можно увидеть, что последовательно прове-

денные операции — отражение в плоскости симметрии т

и последую-

щий перенос на величину вектора j

—

переведут фигуру 1 в положение

2 и далее

—

в 3. Поскольку фигуры Ги 3 оказываются энантиоморфными,

то результирующая операция симметрии, их связывающая, будет опе-

рацией II рода, задаваемой плоскостью симметрии m ', расположенной

между этими (1 и 3) фигурами параллельно исходной плоскости т и от-

1 -

стоящей от нее на половину заданного трансляционного вектора —

—

7J,.

Как видим, трансляция не только размножает (транслирует) элемен-

ты симметрии, но и взаимодействует с ними. В результате появляется

новый, неэквивалентный исходному элемент симметрии на середине

трансляционного вектора. Это хорошо иллюстрирует графическая рабо-

та голландского художника М. Эшера (рис.

6.25).

При взаимодействии плоскостей симметрии в качестве порожденных

элементов возникнут оси 2-го порядка, характер и положение которых

будут зависеть от типа пересекающихся порождающих плоскостей сим-

метрии.

Задав вначале плоскости первых двух позиций символа и получив

результирующую ось 2-го порядка, мы таким образом вычертим график

одной из гемиморфных групп. Последующее взаимодействие элементов

симметрии гемиморфной группы с заданной горизонтальной плоскос-

тью обусловит возникновение целой серии характерных для голоэдри-

ческих пространственных групп дополнительных элементов симметрии:

горизонтальных осей 2-го порядка и центров инверсии.

В качестве примера рассмотрим построение графика пространствен-

ной группы Рта2 = C\

ill,

Ъ/2

Рис.

6.24. К взаимодействию зеркальной плоскости симметрии m

с перпендикулярным ей трансляционным вектором f

Глава 6. Основы кристаллохимии

295

Рис.

6.25. На рисунке Эшера хорошо видна неэквивалентность зеркальных плоскостей

симметрии: например, плоскости, проходящие через летучих мышей, отличаются

от плоскостей, проходящих через бабочек. При этом плоскости одного сорта

располагаются на середине перпендикулярного к ним трансляционного

вектора ("f ), связывающего плоскости другого сорта

Вычертив в масштабе элементарную ячейку (а Ф Ь, у = 90°), нанесем

на график (рис. 6.26а) записанные в символе вертикальные плоскости

т на.

Размножим заданные плоскости перпендикулярными к ним коорди-

натными трансляционными векторами Т

и Т

Таким образом, элементар-

ная ячейка окажется оконтуренной заданными плоскостями (рис.

6.266).

За счет взаимодействий исходных плоскостей с векторами f

и 1],

появятся дополнительные плоскости такого же наименования на их се-

рединах (рис. 6.26«):

тп

- Т

—>

на расстоянии ,

т f

•

1у

—>

на расстоянии —'- .

Взаимодействие двух взаимно перпендикулярных плоскостей т

•

а^

приведет к появлению результирующей оси 2-го порядка, характер ко-

торой определяется вертикальными трансляционными составляющими

296

Кристаллография и кристаллохимия

взаимодействующих плоскостей симметрии. Однако поскольку обе вза-

имодействующие плоскости (т

•

а) не содержат в качестве своих транс-

ляционных компонент вектор t

(а = т

•

), то результирующая ось 2

параллельная линии пересечения исходных плоскостей, не изменит

свой поворотный характер. Однако за счет взаимодействия этой оси с

перпендикулярным ей вектором t

(трансляционной компонентой пло-

скости а) она будет перенесена на середину этого вектора и окажется

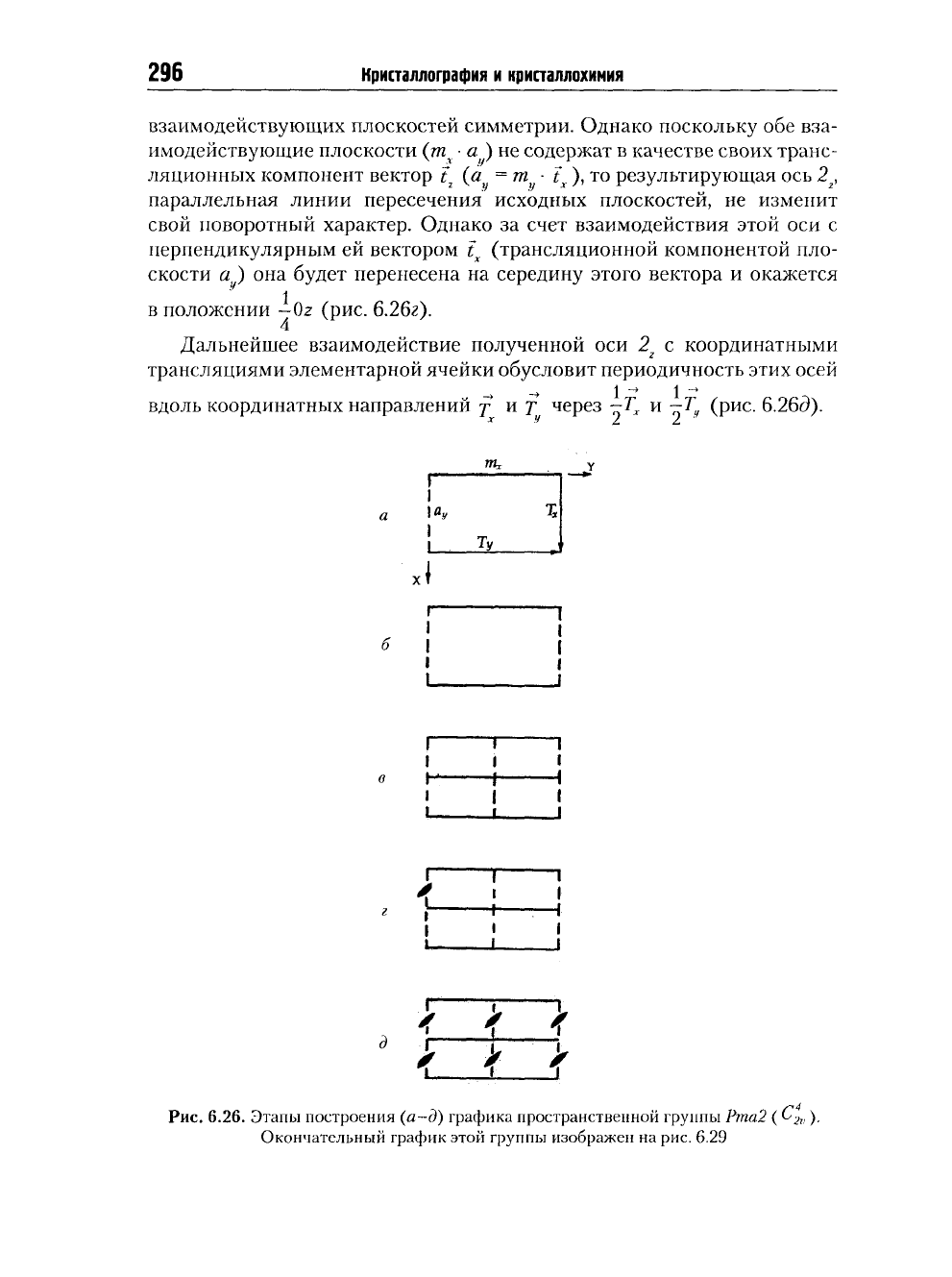
в положении -^Oz (рис. б.26г).

Дальнейшее взаимодействие полученной оси 2

с координатными

трансляциями элементарной ячейки обусловит периодичность этих осей

вдоль координатных направлений j и f через \-Т

и ^-Т

(рис. 6.26Э).

ГПх Y

а \*У

I—

б I

о | ' [ \

1—

Рис.

6.26. Этапы построения (я-Э) графика пространственной группы Рта2 ( с

, ).

Окончательный график этой группы изображен на рис. 6.29

Глава

Основы кристаллохимии

297

Таким образом оказывается построенным график гемиморфной груп-

пы Рта2(С;,

;

Выбор начала координат

Важным этапом вычерчивания графиков пространственных групп

симметрии является выбор начала координат.

соответствии

со

стан-

дартом, принятым

Интернациональных таблицах, начало координат

выбирают

самой высокосимметричной

максимально фиксированной

(т.

е.

самой неподвижной

— с

минимальным числом степеней свободы)

точке.

При

этом число степеней свободы указывает

на

количество

ко-

ординатных направлений, передвигаясь вдоль которых точка

не

меняет

своей симметрии.

Качественной оценкой симметричности

той или

иной позиции

дан-

ной пространственной группе является наличие пересекающихся

этой

точке конечных (макро-) элементов симметрии,

т. е. ее

точечной группы

симметрии. Количественной

же

мерой служит

так

называемая величина

симметрии, характеризующая симметрию данной позиции,

т. е.

порядок

(размножающая способность) точечной группы. Например, порядок

то-

чечной группы

ттт = 8, т = 2 и т. д.

Если позиции имеют одинаковую величину симметрии,

то

предпо-

чтение

при

выборе начала координат отдается наиболее неподвижной

из

них, т.

е.

имеющей наименьшее количество степеней свободы. Например,

позиция, совпадающая

центром инверсии

(величина симметрии

нет степеней свободы), предпочтительнее точки, расположенной

на оси

2-го порядка (величина симметрии

= 2,

одна степень свободы), далее идет

точка

на

зеркальной плоскости симметрии

(величина симметрии

2, две

степени свободы)

и т. д.

Выбор начала координат

гемиморфных группах

не

всегда однозначен,

так

как

отсутствие центров инверсии заставляет выбрать

для

него услов-

ную точку

на

поворотной

оси

2-го порядка (если

она

присутствует),

т. е. в

позиции с одной степенью свободы (точку с одной нефиксированной коор-

динатой). При отсутствии поворотных осей 2-го порядка начало координат

выбирается

на

плоскости симметрии

(как, например,

пространственной

группе Ртс2

(рис. 6.27а)).

При

этом, если возможно, такую точку обычно

выбирают

на

винтовой оси

1(z)

расположенной

плоскости

, или на

ли-

нии пересечения плоскостей

п^ (как

пространственной группе Ртп2

(рис.

6.2761)) для

облегчения сопоставления

соответствующей голоэдри-

ческой надгруппой. Однако такое положение выбранной

качестве нача-

ла координат точки

не

повышает

ее

величину симметрии

и не

уменьшает

число степеней свободы,

т. е. она

остается эквивалентной любой другой

точке, расположенной

на

плоскости

(точка

1 на

рис.

6.28).

Если точ-

ка расположена

на

трансляционном элементе симметрии

(на

плоскости

298

Кристаллография

кристаллохимия

скользящего отражения

или

винтовой

оси)

(точка

2 на

рис.

6.28), то она

ведет себя

так

же,

как

точка общего положения (точка

3), т. е.

размножа-

ется этим элементом симметрии

и не

фиксируется

им,

тогда

как

точка

расположенная

на

макроэлементе симметрии, — точка частного положе-

ния

—

зафиксирована

и им не

размножается (рис.

6.28).

•S !

1 \

j j

Ртс2

{

i—

—i—

H I I 1

...

•

...

^—— (-1

Pmn2j

Pca2

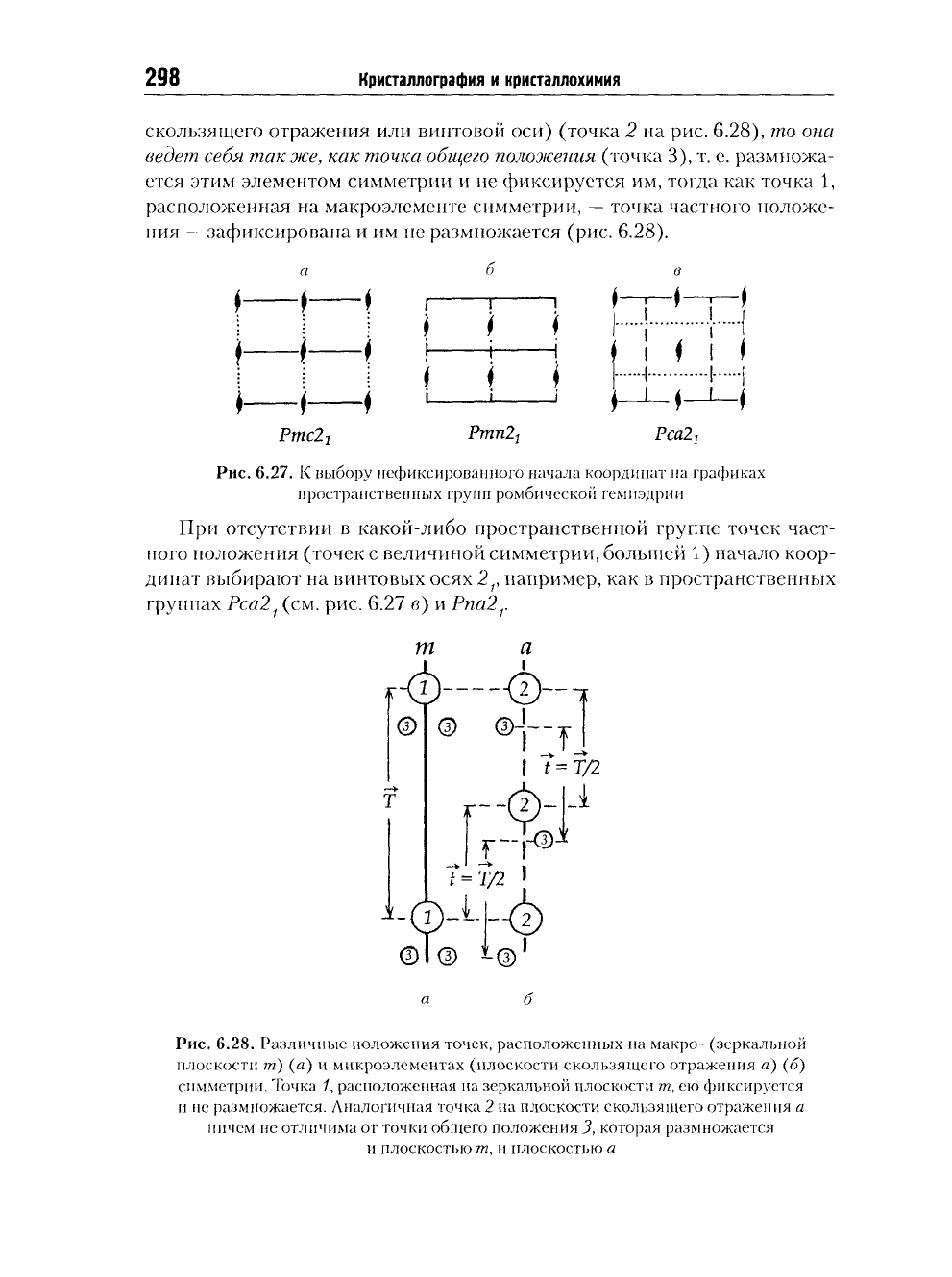
Рис.

6.27. К

выбору нефиксированного начала координат

на

графиках

пространственных групп ромбической гемпэдрии

При отсутствии

какой-либо пространственной группе точек част-

ного положения (точек

величиной симметрии, большей

начало коор-

динат выбирают

на

винтовых осях

, например,

как в

пространственных

группах Рса2

(см. рис.

6.27 в) и

Рпа2

= Т/2

©I®

^©

Рис.

6.28.

Различные положения точек, расположенных

на

макро- (зеркальной

плоскости

т) (а) и

микроэлементах (плоскости скользящего отражения

а) (б)

симметрии. Точка

расположенная

на

зеркальной плоскости

т, ею

фиксируется

не

размножается. Аналогичная точка

2 на

плоскости скользящего отражения

ничем

не

отличима

от

точки общего положения

которая размножается

и плоскостью

т, и

плоскостью

Глава 6. Основы кристаллохимии

299

Следуя выше сформулированным правилам выбора начала коорди-

нат, нетрудно понять, что на графике гемиморфной пространственной

группы Рта2 (рис. 6.26Э) отсутствуют нонвариантиые точки, т. е. точки

без степеней свободы. Из двух же точек частного положения с симмет-

рией 2 и т в качестве начала координат выбирается точка на поворот-

ной оси 2 — точка с одной степенью свободы. После этого график искомой

пространственной группы перерисовывается с новым началом координат.

Правильные системы точек и их характеристики

Определение пространственной группы симметрии соединения еще

не дает представления о его кристаллической структуре. Поэтому, также

как при описании кристаллических многогранников, кроме указания их

точечной группы симметрии приводятся сведения о расположении граней

относительно элементов симметрии, т. е. характеристика простых форм,

участвующих в огранке кристалла. При описании кристаллических струк-

тур помимо отнесения их к одной из 230 пространственных групп симмет-

рии необходимо привести сведения о расположении атомов относительно

элементов симметрии структуры (т. е. их координаты). Так же как огранка

кристаллов представлена в общем случае комбинацией нескольких про-

стых форм, так и кристаллическая структура является комбинацией се-

мейств атомов, каждое из которых получено размножением исходного

атома операциями симметрии данной пространственной группы. Каждое

семейство атомов, занимающее определенную совокупность эквивалент-

ных позиций, называется правильной системой точек или системой экви-

валентных точек

. Правильные системы точек являются как бы микро-

аналогами простых форм кристаллов, так же как 230 пространственных

групп являются микроаналогами 32 точечных групп симметрии.

Подобно тому как положения граней простых форм кристаллов мож-

но характеризовать как частные, т. е. расположенные перпендикулярно

или параллельно каким-либо элементам симметрии либо равноиаклон-

но к эквивалентным элементам симметрии точечной группы (см. пара-

граф 4.1), или общие, для которых не выполняются эти условия, так и в

структурах кристаллов атомы могут занимать частные или общие пра-

вильные системы точек.

Основной характеристикой правильной системы точек служит

симметрия позиции, т. е. комплекс тех элементов симметрии, которые, про-

ходя через точку, расположенную в данной позиции, не размножают ее. Та-

кими (не размножающими) могут быть лишь элементы макросимметрии,

и их сочетание оказывается одной из 32 точечных групп симметрии.

В современной кристаллографической литературе правильные системы

точек иногда называют орбитами.