Егоров-Тисменко Ю.К. Кристаллография и кристаллохимия

Подождите немного. Документ загружается.

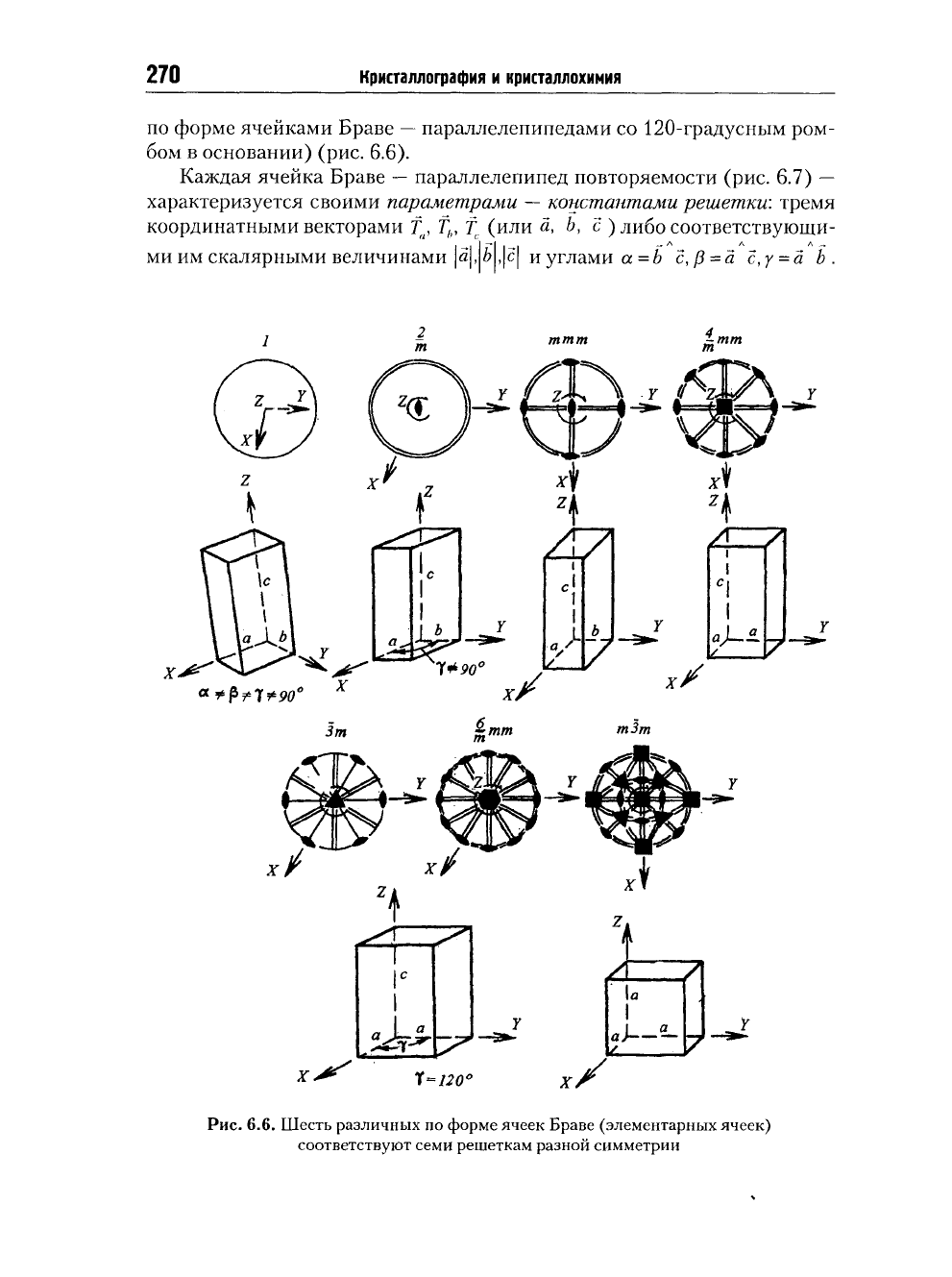
270

Кристаллография и кристаллохимия

по форме ячейками Браве

—

параллелепипедами со 120-градусным ром-

бом в основании) (рис. 6.6).

Каждая ячейка Браве — параллелепипед повторяемости (рис. 6.7) —

характеризуется своими параметрами — константами решетки: тремя

координатными векторами f

, f

(или а, Ь, с ) либо соответствующи-

ми им скалярными величинами |а|,Ы,|с| иугламиа=6 с,В-а с,у

а Ь.

Рис.

6.6. Шесть различных по форме ячеек Браве (элементарных ячеек)

соответствуют семи решеткам разной симметрии

Глава 6. Основы нристаллохимии

271

Рис.

6.7. Параметры решетки (ячейки Браве)

—

ребра a b с

углы между

ними а, (3, у

Иногда в качестве параллелепипеда повторяемости используют так

называемую основную ячейку, построенную на трех последовательных

минимальных трансляциях решетки: а <Ь <с . Однако собственная

mm mm min

симметрия такого параллелепипеда не всегда полностью отражает глав-

ную особенность решетки — ее симметрию. Поэтому основная ячейка не

всегда является ячейкой Браве.

Для полной характеристики пространственной решетки необходимо

кроме ее точечной группы симметрии установить и трансляционный ком-

плекс, т. е. выявить все возможные случаи расположения узлов в ячейке.

6.2.3.

Типы решеток Браве

Если ребра ячейки Браве соответствуют трем последовательным ми-

нимальным трансляциям, т. е. узлы решетки располагаются только в вер-

шинах параллелепипеда, то такая «пустая» ячейка (и соответственно ре-

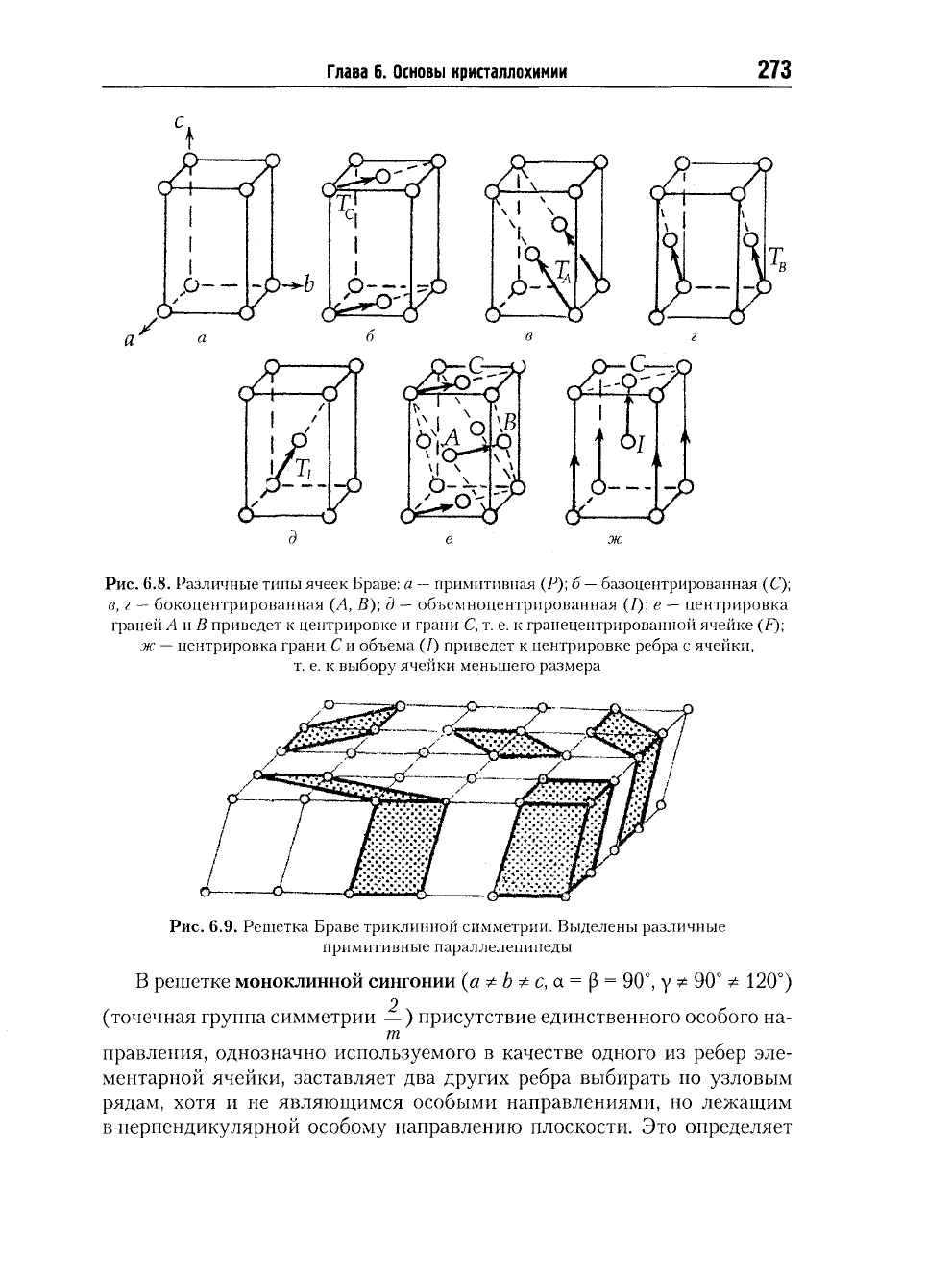
шетка) называется примитивной и обозначается буквой Р (рис. 6.8а).

Если же координатные трансляции ячейки Браве не соответствуют

трем последовательным минимальным трансляциям, т. е. в ячейке есть

более короткие (не координатные!) векторы

, то в ней кроме вершинных

окажутся дополнительные узлы. Указанная ячейка (а следовательно,

и решетка) будет непримитивной.

Обратим внимание на то, что в вершинных узлах ячеек Браве как точ-

ках пересечения векторов максимальной симметрии будут сосредоточены

все элементы симметрии соответствующей голоэдрической точечной груп-

пы.

А так как дополнительные узлы связаны трансляциями с вершинными

Такие дополнительные векторы не могут быть получены как векторные

суммы исходных координатных векторов.

272

Кристаллография

кристаллохимия

узлами

и,

следовательно, идентичны

им, они

могут располагаться лишь

в таких позициях,

которых голоэдрический (полносимметричный)

комплекс решетки представлен либо полностью, либо своей максималь-

ной подгруппой, содержащей главную (или одну

из

главных) ось симмет-

рии. Такие позиции находятся лишь

центрах ребер, граней

или

объема

ячейки. Поэтому ячейки

дополнительными узлами принято называть

центрированными.

При

этом наличие дополнительных узлов

не

наруша-

ет симметрию решетки

и не

уменьшает объем ячейки.

Центрировка ребер

не

имеет смысла,

так как

сократит координатные

трансляции решетки

приведет

выбору ячейки меньшего размера.

Если

ячейке зацентрировать лишь одну грань,

то

возникший транс-

ляционный вектор зацентрирует

противоположную грань

(рис. 6.86).

Так, если зацентрирована пара противоположных граней, перпенди-

кулярных

оси Z

ячейки —

ее

базис,

то

такую ячейку

(и

соответственно

решетку) называют базоцентрированной

обозначают буквой

(цент-

рированы грани

(001) и (001)).

Если зацентрированы боковые грани,

то

такая ячейка называется бокоцептрированной

обозначается либо бук-

вой

(узлы

на

гранях

(100) и

(ТОО), либо буквой

(узлы

на

гранях

(010)

и (ОТО (рис. 6.8в,

г).

Ячейку

дополнительным узлом

центре

ее

объема называют

объ-

емноцентрированной

обозначают буквой

(рис. 6.8Э).

Одновременная центрировка двух

пар

граней (например,

А и В)

(рис.

6.8е)

приводит

возникновению трансляции

АВ,

которая автома-

тически обеспечивает центрировку

грани

С.

Такие ячейки,

которых

центрированы

все

грани, называются гранецентрированными

обозна-

чаются буквой

Одновременная центрировка базиса ячейки

(С) и ее

объема

(Г)

(рис.

6.8ж) или

всех граней ячейки

объема приведет

появ-

лению укороченных векторов (например, вектор

1С), по

которым можно

выбрать параллелепипед меньшего объема.

Остановимся подробнее

на

некоторых моментах вывода решеток Бра-

ве,

рассмотрев

все

возможные позиции

для

дополнительных узлов

эле-

ментарных ячейках всех сингоний (систем),

покажем,

что не

всякая

центрировка ячейки приведет

оригинальной решетке.

В решетке триклинной сингоний

(а

С,

у)

(точечная группа

симметрии

7 )

отсутствие особых направлений никаких ограничений на вы-

бор ячейки Браве

не

накладывает, поэтому выбор характеристического

па-

раллелепипеда произволен.

любая триклинная ячейка может быть пред-

ставлена одним

из

косоугольных параллелепипедов минимального объема

без дополнительных узлов

. Отсюда

списке возможных типов решеток

триклинной сингоний будет лишь примитивная

—

Р(рис.

6.9 и 6.13).

Обычно предпочитают ячейку

наиболее короткими ребрами

углами,

минимально приближенными

к 90°.

Глава 6. Основы кристаллохимии

273

д е ж

Рис.

6.8. Различные типы ячеек Браве: а — примитивная (Р); б — базоцентрированная (С);

в, г — бокоцентрированная (А, В); д — объемноцентрированная (I); е — центрировка

граней Аи В приведет к центрировке и грани С, т. е. к гранецентрированной ячейке (F);

ж — центрировка грани Си объема (/) приведет к центрировке ребра с ячейки,

т. е. к выбору ячейки меньшего размера

Рис.

6.9. Решетка Браве триклинной симметрии. Выделены различные

примитивные параллелепипеды

В решетке моноклинной сингонии (О.ФЬФС, а =

= 90°, у Ф 90° Ф 120°)

(точечная группа симметрии — ) присутствие единственного особого на-

те

правления, однозначно используемого в качестве одного из ребер эле-

ментарной ячейки, заставляет два других ребра выбирать по узловым

рядам,

хотя и не являющимся особыми направлениями, но лежавшим

в перпендикулярной особому направлению плоскости. Это определяет

274

Кристаллография и кристаллохимия

косоугольность лишь одной пары граней ячейки Браве. Поэтому для допол-

нительных узлов пригодны лишь позиции в центрах прямоугольных граней

и в центре ячейки. Центрировка косоугольной грани не приведет к новой

решетке (рис. 6.10<з), ибо в этой плоскости особые направления отсут-

ствуют и ребра ячейки поэтому могут быть выбраны по любым узловым

рядам. Центрировка одной из прямоугольных граней, т. е. появление

дополнительного трансляционного вектора, приведет к оригинальной

В-

или Л-решетке. К этим же решеткам при ином выборе координатных

направлений приведет и центрировка объема ячейки. Отметим, что ра-

венство объемов бокоцентрированной и объемноцентрированной ячеек

Браве ни одной из них преимущества не дает, тогда как F- центрировка

приводит к предпочтительности выбора ячейки меньшего размера

—

/или В (А) (рис. 6.10а).

Напомним, что помимо рассмотренной выше рациональной уста-

новки моноклинной ячейки, при которой по единственному особому

направлению выбирается ось Z(ynwi моноклинности у = Х

У), нередко

используется и классическая (минералогическая) установка с особым на-

правлением вдоль оси Ки углом моноклинности

(X\Z),

что меняет обо-

значение центрировки моноклинной ячейки: В (А) = С (Л)

ч|им

(см. па-

раграф

2.8.2).

В решетке ромбической сингоний (а Ф b Ф с, а = (3 = у = 90°) (то-

чечная группа симметрии ттт) обязательное присутствие трех взаим-

но перпендикулярных неэквивалентных особых направлений диктует

ортогональную координатную систему и, следовательно, обусловливает

прямоугольную форму параллелепипеда Браве. Введение любого до-

полнительного узла в позицию с симметрией ттт (симметрия вершин-

ного узла), т. е. в центры граней или объема, приведет к появлению до-

полнительных трансляций, не совпадающих с особыми направлениями,

а следовательно, к непримитивным ячейкам Браве: С (А, В) — базо(боко)-

центрированной, F

—

гранецентрированной или / — объемноцентриро-

ванной (рис.

6.106).

В решетке тетрагональной сингоний (а = ЬФС, а =

= у = 90°) (точеч-

ная группа симметрии — mm) присутствие единственной оси 4-го поряд-

ка, вдоль которой выбирают координатную ось Z, делает эквивалентны-

ми два других перпендикулярных к ней направления — X и Y. Это об-

условливает форму ячейки в виде тетрагональной призмы. Выбор ребер

а и b элементарной ячейки в первую очередь лимитируется минималь-

ными трансляциями в плоскости, перпендикулярной оси 4-го порядка

(оси Z). Это делает некорректным выбор базо- и гранецентрированных

тетрагональных ячеек, которые являются лишь иными аспектами соот-

ветственно Р- и /-ячеек меньшего размера, т. е. С = Р, F = I.

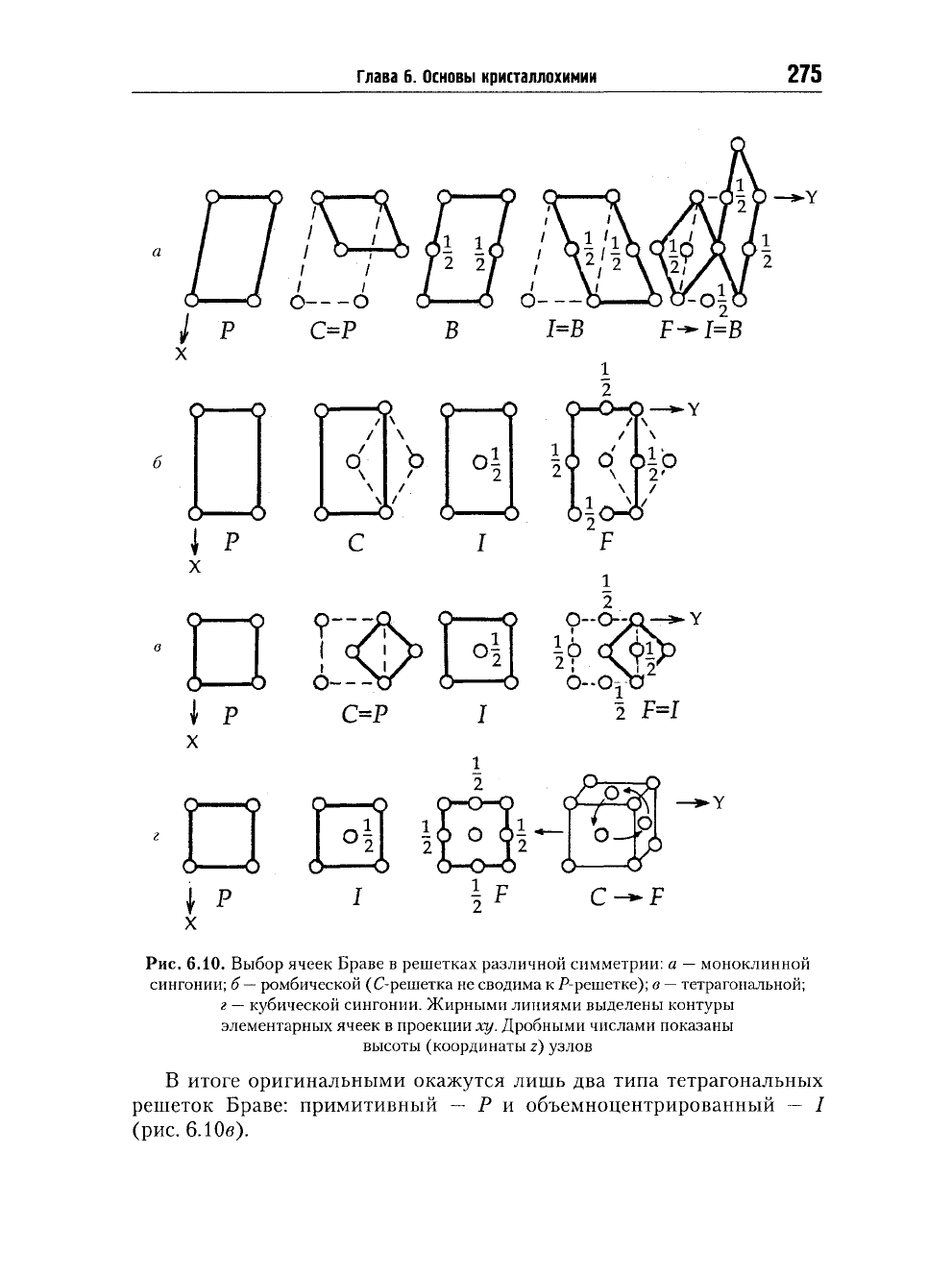
Глава 6. Основы кристаллохимии

275

°1

С — F

Рис.

6.10. Выбор ячеек Браве в решетках различной симметрии: а — моноклинной

сингонии; б

—

ромбической (С-решетка не сводима к Р-решетке); в — тетрагональной;

г — кубической сингонии. Жирными линиями выделены контуры

элементарных ячеек в проекции ху. Дробными числами показаны

высоты (координаты г) узлов

В итоге оригинальными окажутся лишь два типа тетрагональных

решеток Браве: примитивный — Р и объемноцентрированный — I

(рис.

6.10в).

276

Кристаллография

кристаллохимия

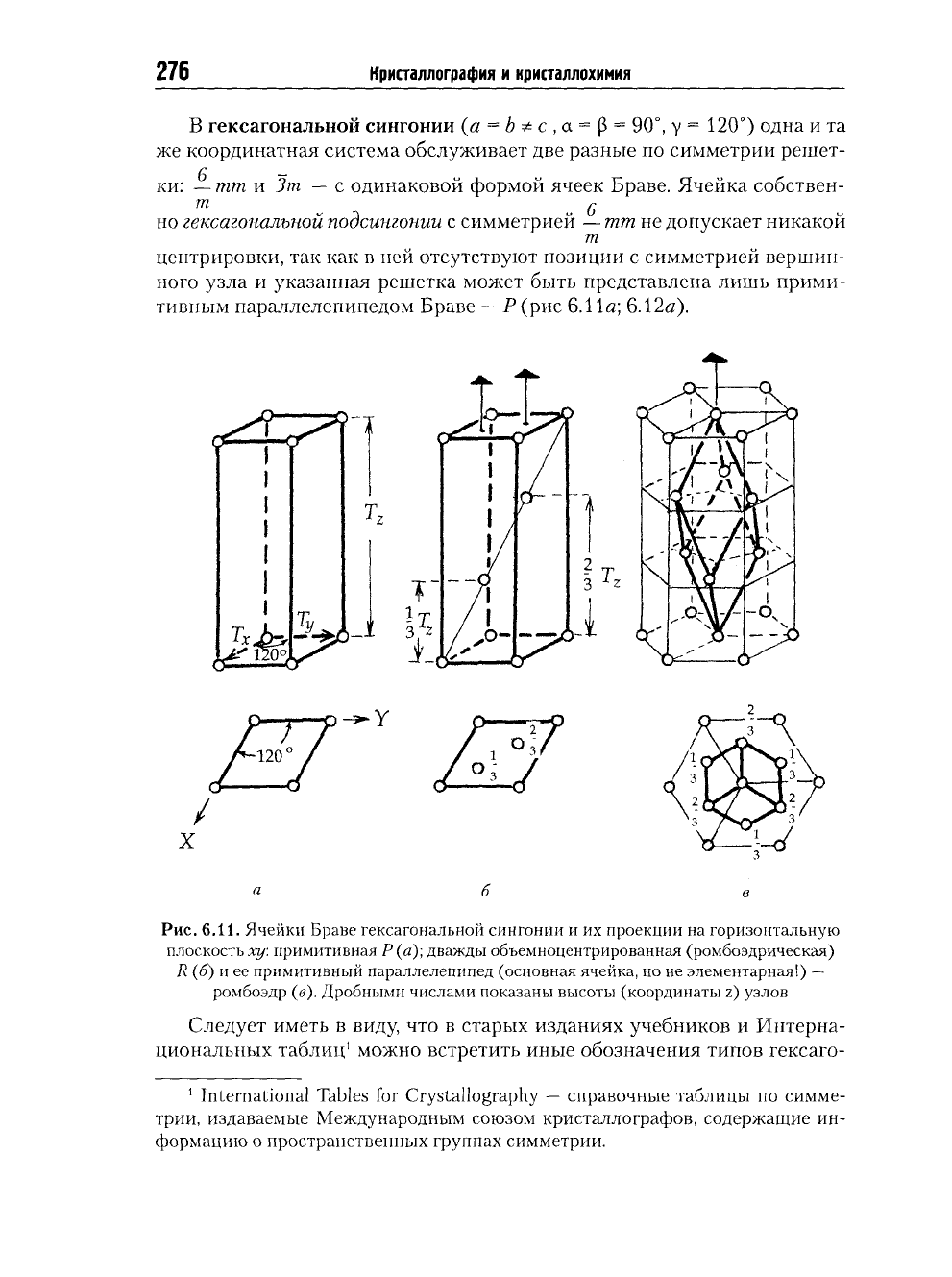
В гексагональной сингонии

(а =

Ь*с,а=$

= 90°, у = 120°)

одна

и та

же координатная система обслуживает

две

разные

по

симметрии решет-

ки:

—

mm и Зт — с

одинаковой формой ячеек Браве. Ячейка собствен-

но гексагональной подсингонии

симметрией —

mm не

допускает никакой

центрировки,

так как в ней

отсутствуют позиции

симметрией вершин-

ного узла

указанная решетка может быть представлена лишь прими-

тивным параллелепипедом Браве

—

Р(рис 6.11а; 6.12а).

б в

Рис.

6.11.

Ячейки Браве гексагональной сингонии

и их

проекции

на

горизонтальную

плоскость

ху:

примитивная

Р(а);

дважды объемноцентрированная (ромбоэдрическая)

R (б) и ее

примитивный параллелепипед (основная ячейка,

но не

элементарная!) —

ромбоэдр

(в).

Дробными числами показаны высоты (координаты

узлов

Следует иметь

виду,

что в

старых изданиях учебников

Интерна-

циональных таблиц

можно встретить иные обозначения типов гексаго-

International Tables for Crystallography —

справочные таблицы

по

симме-

трии, издаваемые Международным союзом кристаллографов, содержащие

ин-

формацию

пространственных группах симметрии.

Глава 6. Основы кристаллохимии

277

нальных решеток. Поскольку гексагональной элементарной ячейкой

считался не параллелепипед, построенный на трех координатных транс-

ляциях, а гексагональная призма (рис.

6.126),

в центре базисной грани ко-

торой оказывался узел решетки, то такая «базоцентрированная» ячейка

обозначалась буквой С.

Иногда в гексагональной решетке в качестве параллелепипеда по-

вторяемости выбиралась также базоцентрированная, но ортогональная

ячейка (аФ ЬФ с, а = (3 = у = 90°, где b = ал/3) ( рис. 6.12е), которая обозна-

чалась также буквой С. Однако все указанные решетки характеризуются

одним и тем же примитивным параллелепипедом — ячейкой Браве

—

с параметрами а = b Ф с, а = (3 = 90°, у =120° (рис. 6.12а). Современное

обозначение такой ячейки (и соответственно решетки)

—

Р.

Кроме рассмотренных установок (и обозначений — С) нередко упо-

треблялась дважды базоцентрированная ячейка Н (рис. 6.12г), ребра

которой расположены под углом 30° к координатным осям стандартной

Р-ячейки, т. е. направлены по ее длинным диагоналям. Обращение к Н-

ячейке снимает противоречие между классической кристаллографией,

опирающейся на минералогию, требующей, чтобы в гексагональной

сингоний за оси ХиУ принимались направления, перпендикулярные к

плоскости симметрии, и современным подходом к написанию символов

гексагональных групп, при котором координатные оси выбираются по

кратчайшим трансляциям и могут не совпадать с нормалями к плоско-

стям симметрии. В этом случае координатная позиция в символе группы

оказывается пустой и заполняется единицей — символом оси 1-го по-

рядка. Выбор укрупненной //-ячейки формально удовлетворяет требо-

ваниям минералогов, переводя особое направление (нормаль к плоско-

сти симметрии) на нужную — вторую — позицию символа. Например,

РЗ 1т = НЗт 1,Р6 2т=Н6т2.

,о-

С С

О L

4jP

Рис.

6.12. Различный выбор элементарных ячеек (выделены жирными линиями)

в решетке гексагональной симметрии: а — примитивная ячейка Браве (Р);

—

гексагональная базоцентрированная призма (Q; а

—

базоцентрированная

ортогональная ячейка (С); /.

—

дважды базоцентрированная ячейка (Н)

278

Кристаллография

кристаллохимия

Ячейка Браве тригональной под сингонии

(Зт) не

может быть при-

митивной,

так как в ней

обязательно должны присутствовать дополни-

тельные узлы, снижающие симметрию решетки

от

—

mm до Зт.

Такие

узлы могут находиться лишь

позициях

на

осях

3-го

порядка, проходя-

щих через центры тригональных призм ячейки,

т. е. в

позициях

симмет-

рией

Зт (см. рис. 6.116). Это

приводит

появлению новых векторов,

не

сокращающих координатные трансляции ячейки Браве. Таким образом,

11 12 2

дополнительные узлы могут иметь лишь координаты

и (или

212121

333333

), т. е.

располагаться

на

одной

из

длинных диагоналей ячей-

3 3 3 3 3 3

ки

точках

ее

пересечения

осями

3-го

порядка, делящих

эту

диагональ

на

три

равные части. Появление

указанных позициях центров инвер-

сии

(их

симметрия повысится

до Зт) не

нарушит симметрию решетки

не

сократит

ее

координатные трансляции. Такую элементарную ячей-

ку

—

ячейку Браве —

представляемую

ею

решетку называют дважды

объемноцептрированной

или

ромбоэдрической

— R (см. рис.

6.11е),

в со-

ответствии

формой примитивного параллелепипеда повторяемости-

ромбоэдра (основной ячейки,

но не

ячейки Браве

(!)).

В решетке кубической сингонии

(а = b = с, а =

= у = 90°)

(точечная

группа симметрии

тЗт) для

дополнительных узлов (кроме позиции

симметрией

тЗт в

центре объема ячейки Браве, порождающей объем-

ноцентрированнуго /-ячейку) легко выделяются позиции

центрах всех

граней

симметрией максимальной подгруппы

—

тт

- Эти

позиции свя-

заны между собой четверкой осей

3-го

порядка,

что

делает невозможной

центрировку лишь одной пары граней. Предположив

этих позициях до-

полнительные узлы, мы тем самым повышаем их симметрию до симметрии

вершинных узлов (тЗт)ч

при

этом убеждаемся, что

они не

нарушают

ни

координатные трансляции,

ни

симметрию всей решетки. Таким образом,

имеем

три

типа решеток кубической сингонии —

Р,1и

F(CM. рис. 6. Юг).

В итоге получили

типов пространственных решеток

— 14

типов

решеток Браве (рис.

6.13,

табл.

6.1).

Таблица

6.1

Типы решеток Браве

Сингония

Примитивная Базо(боко)цен- Объемноцен-

Гранецент-

трированная трированная рированная

Триклинная Р

— — —

Моноклинная

Р=

(В)* = I

- -

Ромбическая

Р С

(А, В)

Тетрагональная

Р=

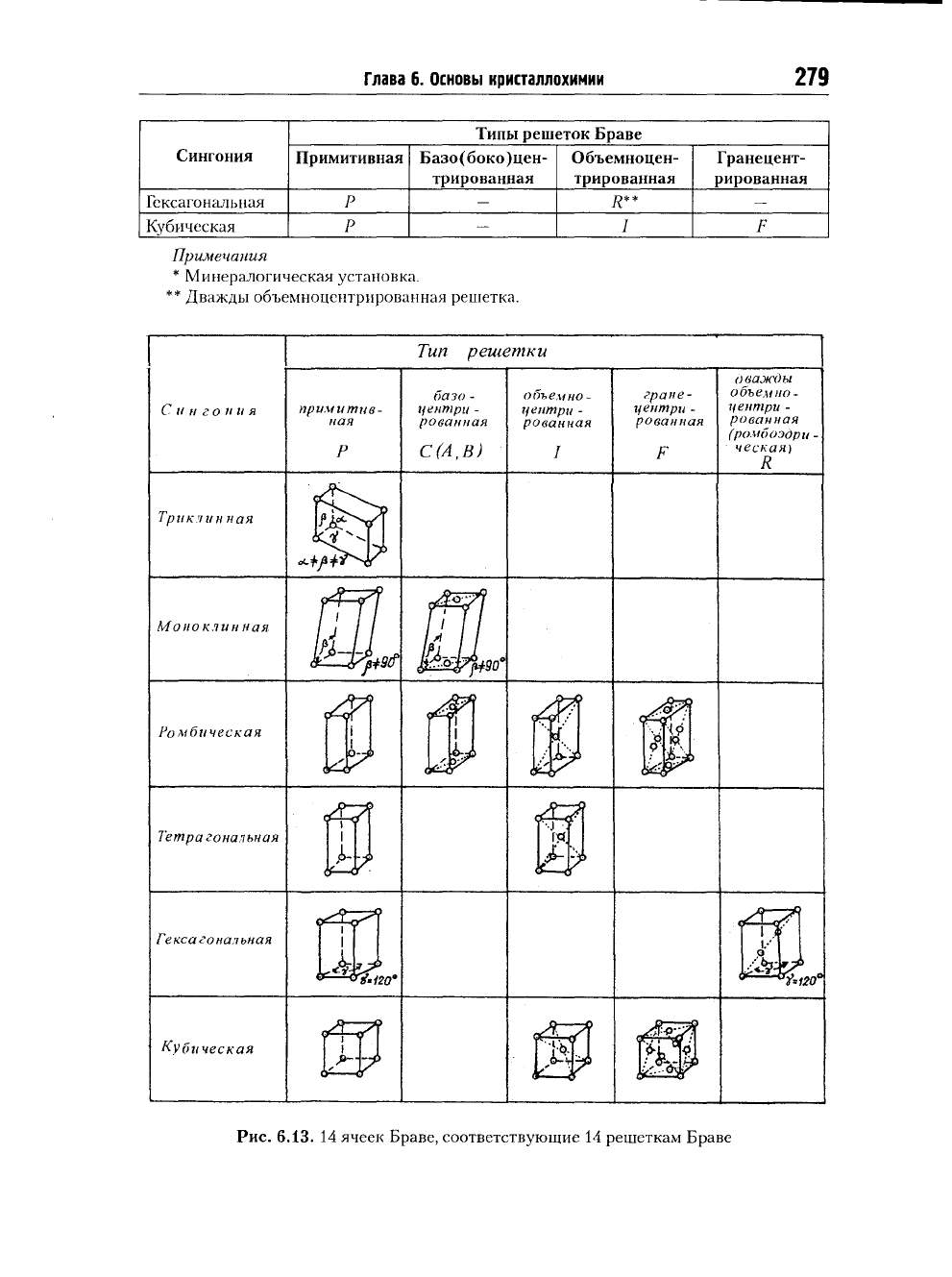
Глава 6. Основы кристаллохимии

279

Типы решеток Браве

Сингония

Примитивная Базо(боко)цен- Объемноцен- Гранецент-

трированная трированная рированная

Гексагональная Р

—

Кубическая Р

Примечания

* Минералогическая установка.

** Дважды объемноцентрированная решетка.

Сингония

Тип решетки

Сингония

примитив-

ная

базо -

центры

рованная

C(A,B)

объемно -

центри

рованная

гране-

центри

рованная

0важ<)ы

объем

но-

центри

рованная

(ромбоэори

ческая)

Триклпиная

Моноклинпая

Ромбическая

им

Тетрагональная

Гекса

гональная

о 1

Кубическая

-1

Рис. 6.13. 14 ячеек Браве, соответствующие 14 решеткам Браве