Егоров-Тисменко Ю.К. Кристаллография и кристаллохимия

Подождите немного. Документ загружается.

280

Кристаллография и кристаллохимия

6.2.4.

Трансляционные элементы симметрии

Информация, сообщаемая типом решетки Браве, недостаточна для

описания кристаллических структур, ибо все кристаллические соедине-

ния обслуживаются всего 14 решетками Браве. А это значит, что одна и

та же решетка описывает большое количество разнообразных структур.

Например, расположение атомов в структурах алмаза С, галита

NaCl,

меди Си описывается одной и той же F-решеткой (рис.

6.14).

Следова-

тельно, нужны дополнительные характеристики, отличающие одну кри-

сталлическую структуру от другой. Действительно, пространственная

решетка — не единственный элемент симметрии, отличающий симмет-

рию кристаллического многогранника от симметрии бесконечной кри-

сталлической структуры. В кристаллических структурах — трехмерных

регулярных постройках

—

легко обнаружить элементы макросимметрии,

используемые при описании симметрии конечных фигур и, в частности,

внешней формы кристаллов: зеркальные плоскости, поворотные и ин-

версионные оси и центр инверсии. Но присутствие в бесконечных по-

стройках трансляций

—

симметрических операций I рода

—

не оставляет

ни одну точку кристаллического пространства (а соответственно, и ни

один элемент симметрии) в единственном числе, а многократно повто-

ряет их (транслирует) в определенных направлениях, создавая таким

образом серии одинаковых элементов симметрии. Кроме того, трансля-

ции взаимодействуют с элементами макросимметрии, в результате чего

образуются специфические для трехмерного бесконечного кристалличе-

ского пространства трансляционные элементы симметрии: винтовые оси

и плоскости скользящего отражения.

Рис.

6.14. Кристаллические структуры алмаза С (я), галита

NaCl

(б) и меди Си (в)

описываются одной и той же гранецентрированной (F) решеткой Браве

Винтовые оси симметрии

Рассмотрим появление винтовых осей на примере взаимодействия

двух операций симметрии I рода — поворота вокруг оси 4-го порядка

Глава б. Основы кристаллохимии

281

и одновременного переноса в параллельном оси направлении, т. е. взаи-

модействие поворота с трансляцией вдоль оси

Размножив произволь-

но взятую точку (фигуру) вокруг вертикальной оси 4-го порядка - 4

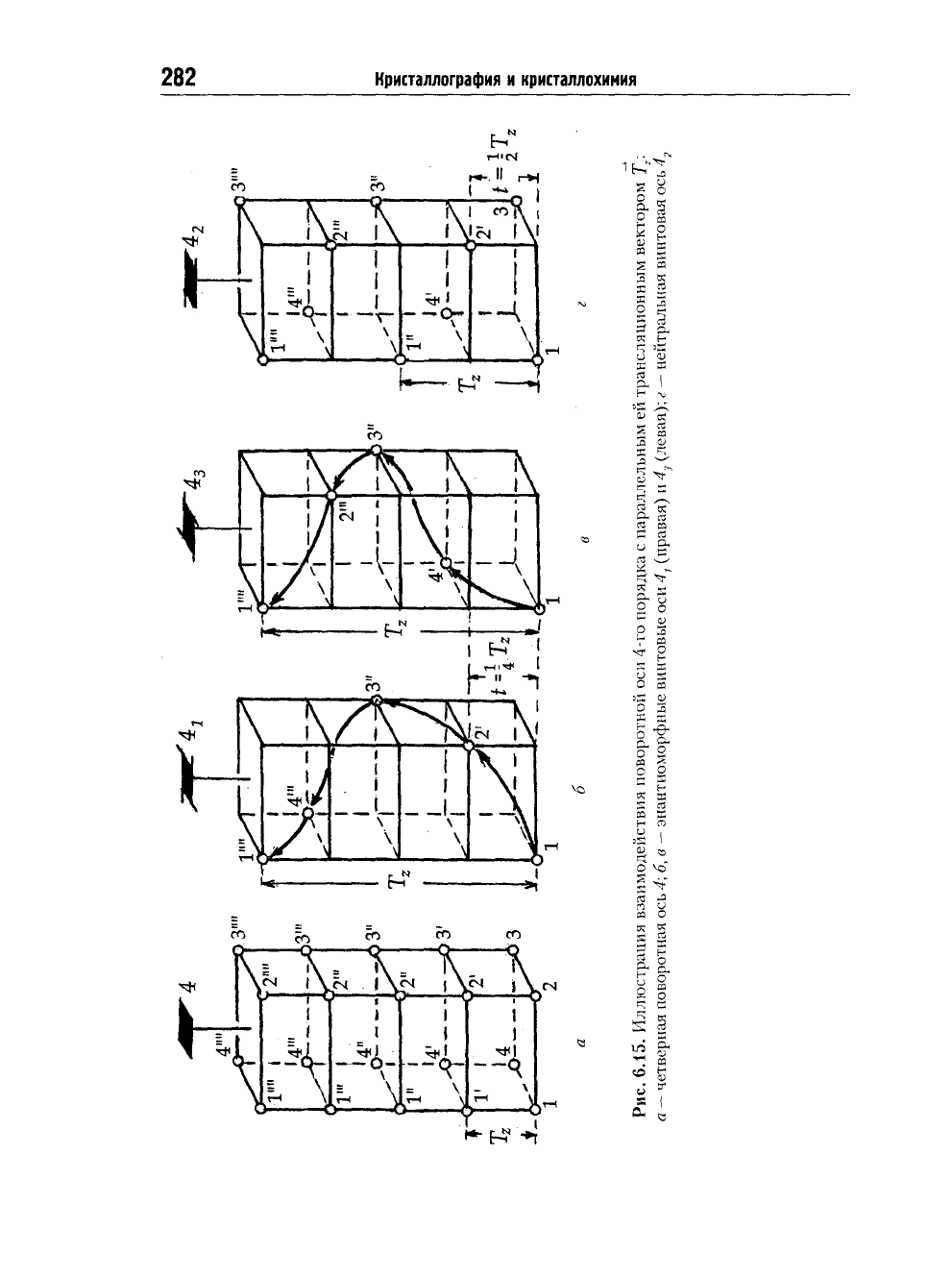
(рис.

6.15а), получим четыре эквивалентные точки 1-4 на одном уров-

не относительно координатной оси Z. Трансляция Т

размножит эти

точки в направлении данной оси: из точки 1 получим точки 1', 1", Г",

\"" и т. д., из точки 2

—

2', 2", 2"' и т. д. В результате возникнут четверки

точек на одном уровне по оси Z: 1', 2', 3', 4' и т. д., связанные поворотом

на 90° вокруг исходной оси 4; точки же, расположенные друг над дру-

гом, — 1, Г, 1" ...

—

связаны вертикальным трансляционным вектором Т

Для того чтобы от точки 1 перейти к точке 2', понадобятся две после-

довательные операции: поворот вокруг оси 4-го порядка на 90° против

часовой стрелки с одновременной трансляцией вдоль оси Z. Поскольку

кристаллографические группы

—

это частный случай абстрактных мате-

матических групп, в которых произведение симметрических операций

группы рассматривается как самостоятельная операция, принадлежа-

щая этой же группе, в данном случае будет иметь место новая симмет-

рическая операция I рода — винтовой поворот — и, соответственно,

новый элемент симметрии, задающий такое сочетание симметрических

операций, — винтовая ось симметрии. Таким образом, в данном случае

поворотная ось 4-го порядка одновременно является и винтовой осью

этого же порядка. Если порождающие элементы симметрии — пово-

ротную ось 4 и трансляцию Т

— убрать, то их произведение — винто-

вая ось симметрии — сохранится в чистом виде (рис.

6.156").

При этом

винтовое движение можно разложить на две в общем случае «мнимые»

симметрические операции: поворот вокруг несуществующей поворот-

ной оси 4-го порядка и перенос, не являющийся трансляцией в этом

направлении, т. е. элементом симметрии. Истинная же трансляция Т

кратное число раз (в данном случае в четыре раза) превысит величи-

ну исходного (мнимого!) переноса t_. Из рис. 6.156 видно, что поворот

на 90° вокруг «мнимой» поворотной оси 4-го порядка сопровождает-

ся переносом вдоль нее на вектор ?

, называемый ходом винтовой оси.

Четырехкратное винтовое движение приведет к точке 1"", связанной с

точкой 1 истинной трансляцией в этом направлении

=4t

Порядок

винтовой оси определяется, как и в случае с поворотными осями, эле-

ментарным углом поворота а. В данном случае имеет место винтовая

ось 4-го порядка, обозначаемая как 4 .

Разнообразие винтовых осей одного и того же порядка, связанное

с величинами векторов i

, отражено в их обозначениях: винтовые оси

обозначаются арабскими цифрами, соответствующими порядку оси,

с нижним цифровым индексом, указывающим, какой части истинной

трансляции Т

соответствует трансляционный вектор i

винтовой оси.

282

Кристаллография и кристаллохимия

Глава

Основы кристаллохимии

283

1 -

Например, если

t =—Т, а

вращение происходит против часовой стрелки

на

90°, то

винтовая

ось

обозначается

(рис. 6.156) и

называется пра-

вой.

Энантиоморфиая

ей ось с

вращением

противоположную сто-

рону

(по

часовой стрелке) называется левой

обозначается

или 4_

так

как

правое вращение

данном случае сопровождается переносом

t =-f

(рис. 6.15в).

Если

же i

2^'

то

винтовая

ось

оказывается нейтральной,

ибо

направление вращения

не

играет

данном случае существенной роли

(рис.

6.15г).

Графически вертикальные винтовые

оси

изображаются соответству-

ющими

их

порядку многоугольниками

«лопастями», указывающими

на направление вращения (рис.

6.16).

\ 3, 3

-^к 4, 4

4, Щ

Рис.

6.16.

Графическое обозначение вертикальных винтовых осей

Плоскости скользящего отражения

Плоскости скользящего отражения можно получить, рассмотрев соче-

тание двух операций симметрии: отражения

плоскости симметрии (опе-

рация

рода)

параллельной

ей

трансляцией — элементом симметрии

бесконечных построек

рода. Если произвольную фигуру

(рис.

6.17)

отразить

зеркальной плоскости симметрии, перпендикулярной

оси X

(mj, то

получим энантиоморфную

ей

фигуру

Трансляция

размно-

жит

эти

фигуры

направлении

оси

из

фигуры

получим фигуру

3, за-

тем

5,7 и

т. д.,

из

фигуры 2

—

фигуры

4,6,8 и

т. д.

Для

того чтобы перейти от

фигуры 1

фигуре

необходимо произвести

две

последовательные сим-

метрические операции: отражение

зеркальной плоскости

перенос

на величину вектора

т. В

итоге результирующим движением окажется

скользящее отражение, а следовательно, появится новый элемент симмет-

рии

рода — плоскость скользящего отражения, задающая

две

простые

симметрические операции: отражение

плоскости симметрии

перенос

в параллельном заданной плоскости направлении

на

определенное рас-

стояние. Отсюда расположение фигур

данном узоре (рис. 6.17а) может

быть описано

не

только

помощью зеркальной плоскости

вектора т

но

и с

помощью сложного элемента симметрии бесконечных построек

—

плоскости скользящего отражения, которая совпадает

плоскостью

284

Кристаллография и кристаллохимия

т. е. «работает» одновременно и как зеркальная плоскость, и как плоскость

скользящего отражения.

Однако если порождающие элементы симметрии (и зеркальную пло-

скость т

, и трансляцию Т ) убрать, то их произведение — плоскость

скользящего отражения — может сохраниться в качестве самостоятель-

ного элемента симметрии (рис.

6.176).

В этом случае оба элемента сим-

метрии, задающие симметрические операции плоскости скользящего

отражения, окажутся «мнимыми» и не существующими раздельно (т. е.

операция отражения задается мнимой зеркальной плоскостью), так же

как и вектор переноса является не реальной трансляцией, а лишь транс-

ляционной компонентой этой плоскости. Однако реальная трансляция,

как основная симметрическая операция кристаллического вещества, со-

всем исчезнуть не может. В данном случае она сохранится, трансформи-

руясь в вектор, равный удвоенному поступанию, т. е. Т

2t , тогда как

двукратно повторенные операции отражения в плоскости скользящего

отражения взаимно уничтожатся, т. е. дадут операцию идентичности

(тп •

m = 1). Отсюда ясно, что величина трансляционной компоненты пло-

скости скользящего отражения всегда равна половине реальной трансля-

ции в этом направлении.

Различают плоскости скользящего отражения двух типов. К перво-

му типу относятся плоскости со скольжением вдоль одного из коорди-

натных направлений. При этом буквами а, Ъ и с обозначаются плоско-

сти со скольжением вдоль координатных осей X, Y и Z соответственно.

а т

\ I

\—I

\ I

\ \

Ту

Рис.

6.17. Взаимодействие двух операций симметрии: отражение в плоскости

симметрии с параллельной ей трансляцией. В первом случае (а) Т

является

реальной трансляцией (элементом симметрии) бесконечной постройки.

Во втором случае (б) t

является лишь составной частью операций

плоскости скользящего отражения и в качестве самостоятельного

элемента симметрии не существует

Глава 6. Основы кристаллохимии

285

С изменением ориентации трансляционной компоненты меняются

и обозначения этих плоскостей. Графически вертикальные плоскости с

горизонтальным скольжением изображаются штриховой линией

(штрихи горизонтальны и параллельны плоскости чертежа) (рис.

6.175;

6.18а; 6.19а), плоскости с вертикальным скольжением (обычно вдоль

оси2)—

пунктирной (точечной ) линией (штрихи перпен-

дикулярны плоскости чертежа) (рис. 6.186 и 6.19а). Горизонтальные

плоскости а и

обозначаются соответственно значками Г

Г*, стрелки

на которых указывают направления трансляционных составляющих

(рис.

6.19а).

Плоскости второго типа характеризуются трансляционными векто-

рами, ориентированными одновременно вдоль двух координатных на-

правлений (т. е. вдоль двух ребер элементарной ячейки), и, следователь-

но,

результирующее скольжение совпадает с диагональю грани (узловой

сетки) элементарной ячейки, образуя косой угол с координатными ося-

ми.

Отсюда название таких плоскостей скользящего отражения

—

клино-

плоскости (от греч. клино (KXIVCO) — косой).

Различают клиноплоскости двух видов. Клиноплоскости, обозначае-

мые буквой п, содержат трансляционные компоненты, равные полови-

нам координатных трансляций Т

элементарной ячейки. Сам

же вектор скольжения (t ) соответствует половине диагонали «пустой»

(нецентрированной) грани (f ) элементарной ячейки:

а б в г

Рис. 6.18. Действия различных типов плоскостей скользящего отражения:

а — плоскости а; б

—

плоскости с; в — клиноплоскости я; г — клиноплоскости d.

Знаками «+» показаны высоты фигурок (+z) относительно нулевого уровня

по оси Z

286

Кристаллография и кристаллохимия

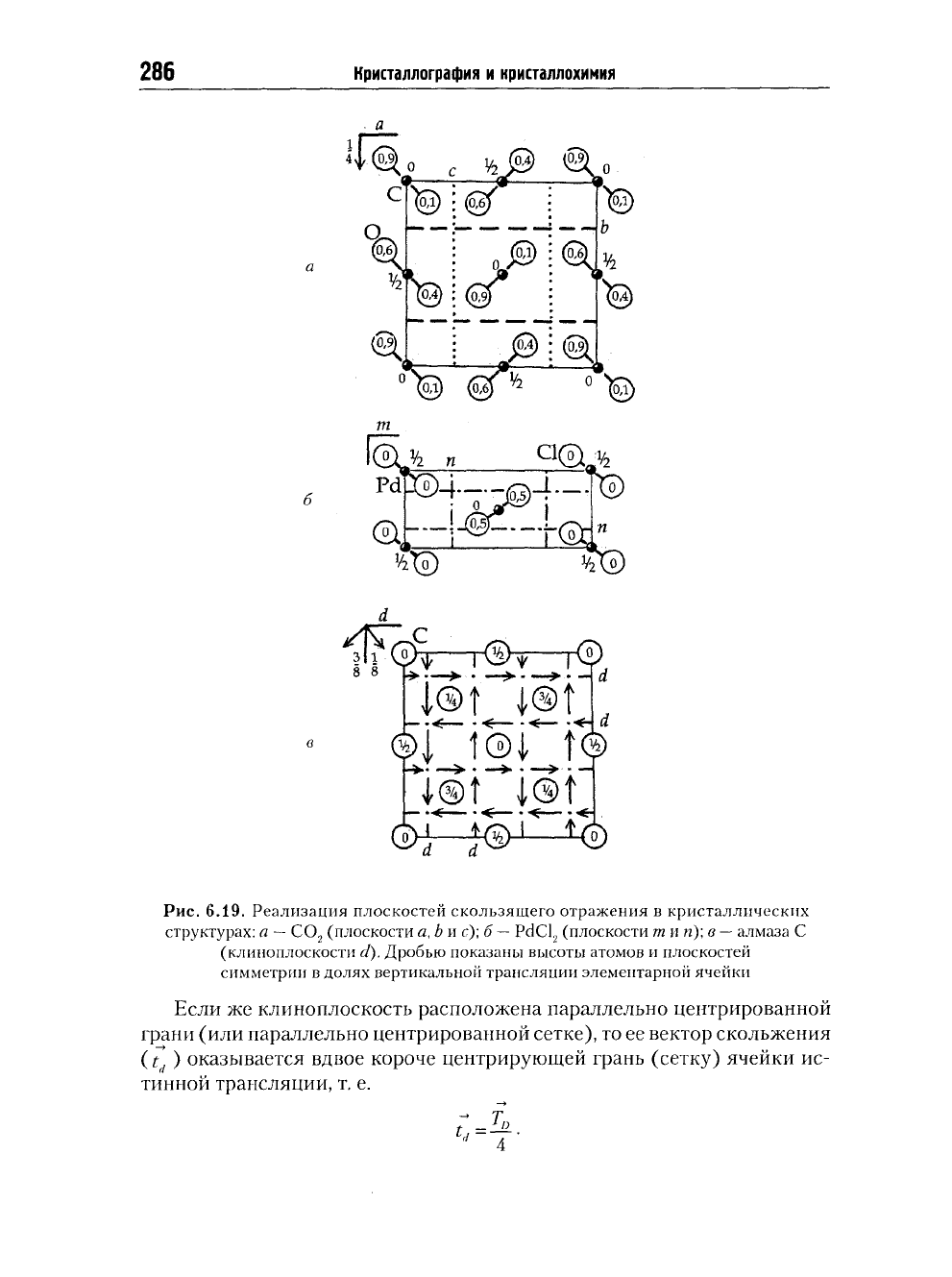
Рис.

6.19. Реализация плоскостей скользящего отражения в кристаллических

структурах: я

—

С0

(плоскости я, b и с); б ~

PdCl,

(плоскости т и и); в

—

алмаза С

(клиноплоскости d). Дробью показаны высоты атомов и плоскостей

симметрии в долях вертикальной трансляции элементарной ячейки

Если же клиноплоскость расположена параллельно центрированной

грани (или параллельно центрированной сетке), то ее вектор скольжения

(t ) оказывается вдвое короче центрирующей грань (сетку) ячейки ис-

тинной трансляции, т. е.

Глава 6. Основы кристаллохимии

287

Такая клиноплоскость обозначается буквой d'.

В отличие от плоскостей a, b и с клиноплоскости п и d не меняют

своего обозначения при изменении наименований координатных осей.

Графически клиноплоскости п обозначаются штрихпунктиром

(рис.

6.18е и

6.196),

в обозначении же плоскостей d каждый штрих заменя-

ется стрелкой, направление которой указывает на увеличение вертикаль-

ной трансляционной составляющей этой клиноплоскости

—>—>—>—>—>

(рис.

6.18г и 6.19е). Горизонтальные клиноплоскости dun обозначаются

значком J^i , где стрелка указывает направление скольжения, а дробь

—

высоту плоскости в долях вертикальной трансляции ячейки.

6.2.5.

Пространственные (федоровские) группы симметрии

При описании симметрии внешней огранки кристаллов используется

понятие «точечная группа симметрии»

(см. параграф 2.6). Взаимодей-

ствие элементов макросимметрии — зеркальных плоскостей, поворот-

ных и инверсионных осей, центра инверсии — приводит к 32 их сочета-

ниям

—

32 классам (точечным группам) симметрии.

Для описания симметрии внутреннего строения кристаллов — их

структур — помимо уже перечисленных макроэлементов симметрии по-

требуются еще трансляционные элементы микросимметрии: прежде все-

го кристаллическая решетка — главный элемент симметрии бесконеч-

ных построек, выявляющий трехмерную периодичность расположения

материальных частиц в кристаллическом пространстве, винтовые оси и

плоскости скользящего отражения. Взаимодействие всех указанных эле-

ментов симметрии приведет к 230 их сочетаниям — 230 пространствен-

ным (федоровским) группам симметрии.

Принцип вывода пространственных групп симметрии

Вывод пространственных групп симметрии посредством простого пе-

ребора всех сочетаний элементов симметрии и типов решеток Браве бу-

дет достаточно сложен и займет много времени. Н. В. Белов предложил

более простой и наглядный способ их вывода на основе использования

основного принципа Ю. В. Вульфа о фундаментальной роли плоскостей

Иногда клиноплоскости d называют алмазными, так как они присутствуют

в структуре алмаза (от англ.

diamond

—

алмаз) (рис. 6.19о).

Точечными группами симметрии называют такие операции симметрии,

при которых хотя бы одна точка пространства инвариантна, т. е. остается непод-

вижной. Так, при операции инверсии, точка, совпадающая с центром инверсии

остается на месте; при отражении в плоскости симметрии точки, принадлежа-

щая этой плосткости, также оказываются неподвижными, так же как точки, рас-

положеные на поворотных осях симметрии.

288

Кристаллография

кристаллохимия

симметрии

как

порождающих элементов симметрии.

Он

предложил «от-

толкнуться»

от 32

точечных групп симметрии,

т. е.,

взяв

за

основу одну

из точечных групп

выделив

в не й

порождающие элементы симметрии,

придавать

им

разные трансляционные компоненты, сочетания которых

с учетом определенного типа решетки Браве

дадут

все

пространствен-

ные группы, подчиненные данной точечной.

Наиболее ярко суть метода, предложенного

Н. В.

Беловым, выступает

при выводе групп ромбической голоэдрии,

так как

ортогональный коорди-

натный репер, максимальное число решеток Браве

присутствие порождаю-

щих неэквивалентных плоскостей симметрии (генераторов пространствен-

ных групп), перпендикулярных всем трем координатным направлениям,

делает такой вывод наиболее наглядным. Все это позволяет распространить

этот метод

и па

вывод пространственных групп остальных сингоний.

В обозначениях пространственных групп

на

первой позиции реги-

стрируется

тип

решетки Браве,

затем

символике Германна-Могена

(в международной символике,

см.

параграф

2.9)

записывается набор

порождающих элементов симметрии

учетом

их

трансляционных раз-

новидностей. Такие обозначения позволяют отразить различия симмет-

рии кристаллических структур соединений, внешняя огранка которых

подчиняется одной точечной группе. Например,

как мы уже

отмечали,

внешняя симметрия кристаллов галита

NaCl,

алмаза, граната описы-

вается одной

и той же

голоэдрической точечной группой

тЗт.

Одна-

ко

их

внутренняя симметрия

—

симметрия кристаллической структу-

ры

—

характеризуется разными пространственными группами:

Fm3m,

Fd3m

Ia3d

соответственно.

В качестве примера рассмотрим вывод пространственных групп ром-

бической голоэдрии, подчиненных точечной группе

международный

2 2 2

символ которой

ттт-

подчеркивает топологическое сходство

ттт

всех трех неэквивалентных особых направлений.

Это

позволяет

при вы-

воде групп перенести акцент

на

направления скольжения

плоскостях

трех позиций международного символа.

Прежде чем начать вывод пространственных групп

примитивной

(Р)

решеткой Браве, следует решить, какие трансляционные разновидности

плоскостей симметрии возможны

на

каждой

из

трех позиций междуна-

родного символа ромбической голоэдрии.

При

этом обратим внимание

на

то,

что плоскости скользящего отражения a,

b и

с с трансляционной компо-

нентой, ориентированной вдоль одной

из

координатных осей, изменяют

свои наименования

зависимости

от той или

иной ориентации

их

компо-

нент

('£ )•

Обозначения

же

клииоплоскостей

п не

меняются

зависимости

от

их

ориентации относительно координатных направлений вследствие

того,

что их

трансляционные компоненты направлены по диагоналям

гра-

Глава

Основы кристаллохимии

289

ней элементарной ячейки,

т. е. не

привязаны

какой-либо определенной

координатной оси. Таким образом, перпендикулярно осиХ, т.

е. на

первой

позиции международного символа, могут располагаться плоскости

т, п,

или

Ь;

на

второй позиции — перпендикулярно

оси Y

—

плоскости

т, п,

или а и на

третьей — перпендикулярно

оси Z

—

плоскости

т, п, а и Ь.

Вывод групп ромбической голоэдрии сведется

определению сочетаний

всех возможных перечисленных выше плоскостей. Однако формальная

перестановка букв приведет

большому количеству групп, значительно

превышающему

их

реальное число из-за того,

что

одна

и та же

группа

разных аспектах будет обозначаться разными символами

(рис.

6.20). Из-

бежать указанных трудностей можно, воспользовавшись рекомендация-

ми

Н. В.

Белова, предложившего следующую схему

их

вывода.

стандартный

аспект

РЬст

Ртса

Рсат

РапЪ

РЬта

РтаЬ

Рис.

6.20.

Различные аспекты пространственной группы РЬст

= ОЦ .

Стрелками показаны направления трансляционных компонент

плоскостей скользящего отражения

Первое семейство пространственных групп составляют комбинации

не меняющих свое наименование

зависимости

от

ориентации элемен-

тарной ячейки плоскостей симметрии —

тип:

Рттт

Рппп

(Dl),

Рттп

(£)") и

Рппт

{).

' Иногда описание

той или

иной кристаллической структуры дается

в не-

стандартной установке.

этом случае

на

помощь приходит символ Шенфлиса,

где надстрочный порядковый номер группы

пределах одного кристаллографи-

ческого класса указывает

на

определенную пространственную группу, выпол-

няя роль своеобразного ключа. Например, структура

PbCl

часто описывается

в аспекте РЬпт,

а не в

стандартном Рпта

( D'

Пространственная группа,

которую перешел весь набор элементов сим-

метрии соответствующей точечной группы, называется симморфной группой.

Например, симморфные группы ромбической голоэдрии: Рттт, Сттт,

Immm,

Fmmm.

Если

к 32

точечным группам приписать типы решеток Браве соответ-

ствующей сингонии,

то

получим

симморфные группы. Например,

триклин-

ной сингонии

их

будет

две: Р1 и Р1 и т. д.

Гемисимморфная группа

—

группа,

в которой сохранился только осевой комплекс точечной группы; асимморфная

группа —

не

сохранились полностью

ни

осевой,

ни

плоскостной комплексы.

К)

- 98