Егоров-Тисменко Ю.К. Кристаллография и кристаллохимия
Подождите немного. Документ загружается.

320
Кристаллография и нристаллохимия
а 6
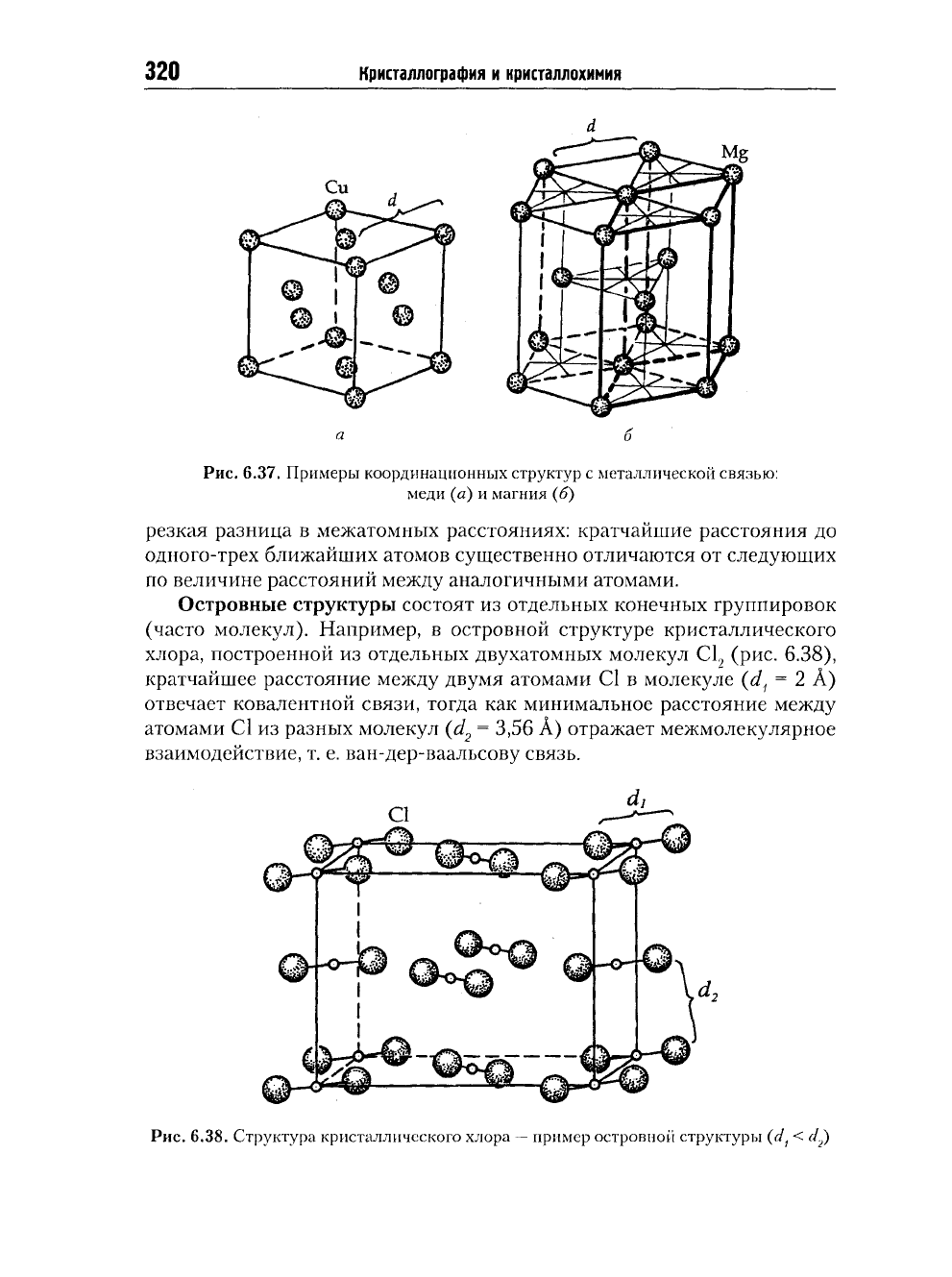
Рис.
6.37. Примеры координационных структур с металлической связью:
меди (а) и магния (б)
резкая разница в межатомных расстояниях: кратчайшие расстояния до
одного-трех ближайших атомов существенно отличаются от следующих
по величине расстояний между аналогичными атомами.
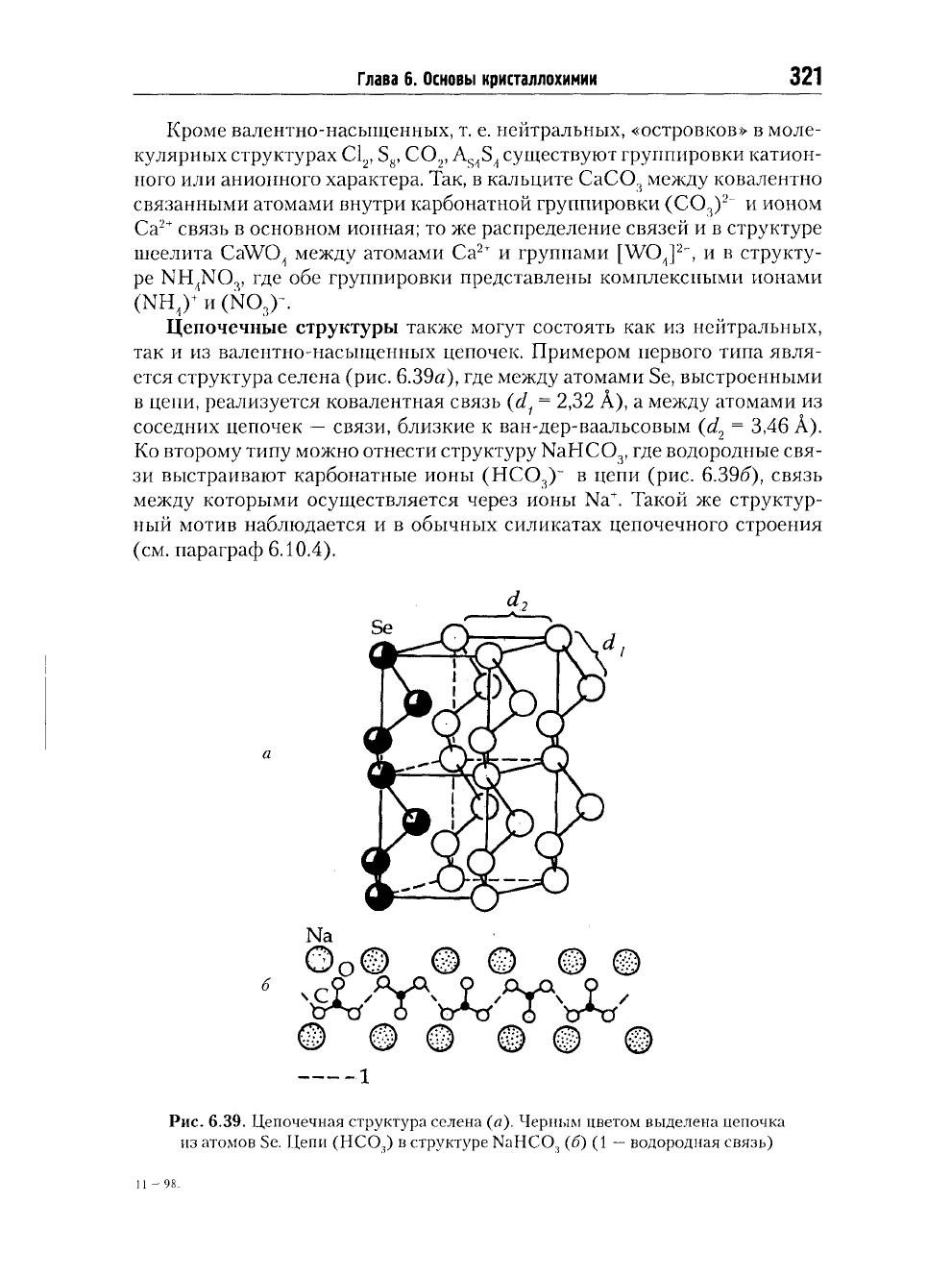
Островные структуры состоят из отдельных конечных группировок
(часто молекул). Например, в островной структуре кристаллического
хлора, построенной из отдельных двухатомных молекул С1
9
(рис.
6.38),
кратчайшее расстояние между двумя атомами О в молекуле (d
1
= 2 А)
отвечает ковалентной связи, тогда как минимальное расстояние между
атомами CI из разных молекул (d
2
= 3,56 А) отражает межмолекулярное
взаимодействие, т. е. ван-дер-ваальсову связь.
Рис.
6.38. Структура кристаллического хлора
—
пример островной структуры (d
t
< d.
2
)
Глава
6.
Основы кристаллохимии
321
Кроме валентно-насыщенных,
т. е.
нейтральных, «островков»
в
моле-
кулярных структурах
Cl
2
,
S
8
,
С0
2
,
A^S,,
существуют группировки катион-
ного
или
анионного характера. Так,
в
кальците
CaCO,
s
между ковалентно
связанными атомами внутри карбонатной группировки (С0
3
)
2
~
и
ионом
Са
2+
связь
в
основном ионная;
то же
распределение связей
и в
структуре
шеелита CaWO,, между атомами
Са
2,
и
группами [WOJ
2
*,
и в
структу-
ре
NH
4
NO
x
,
где обе
группировки представлены комплексными ионами
(NH
4
)
+
H(N0
3
)-.
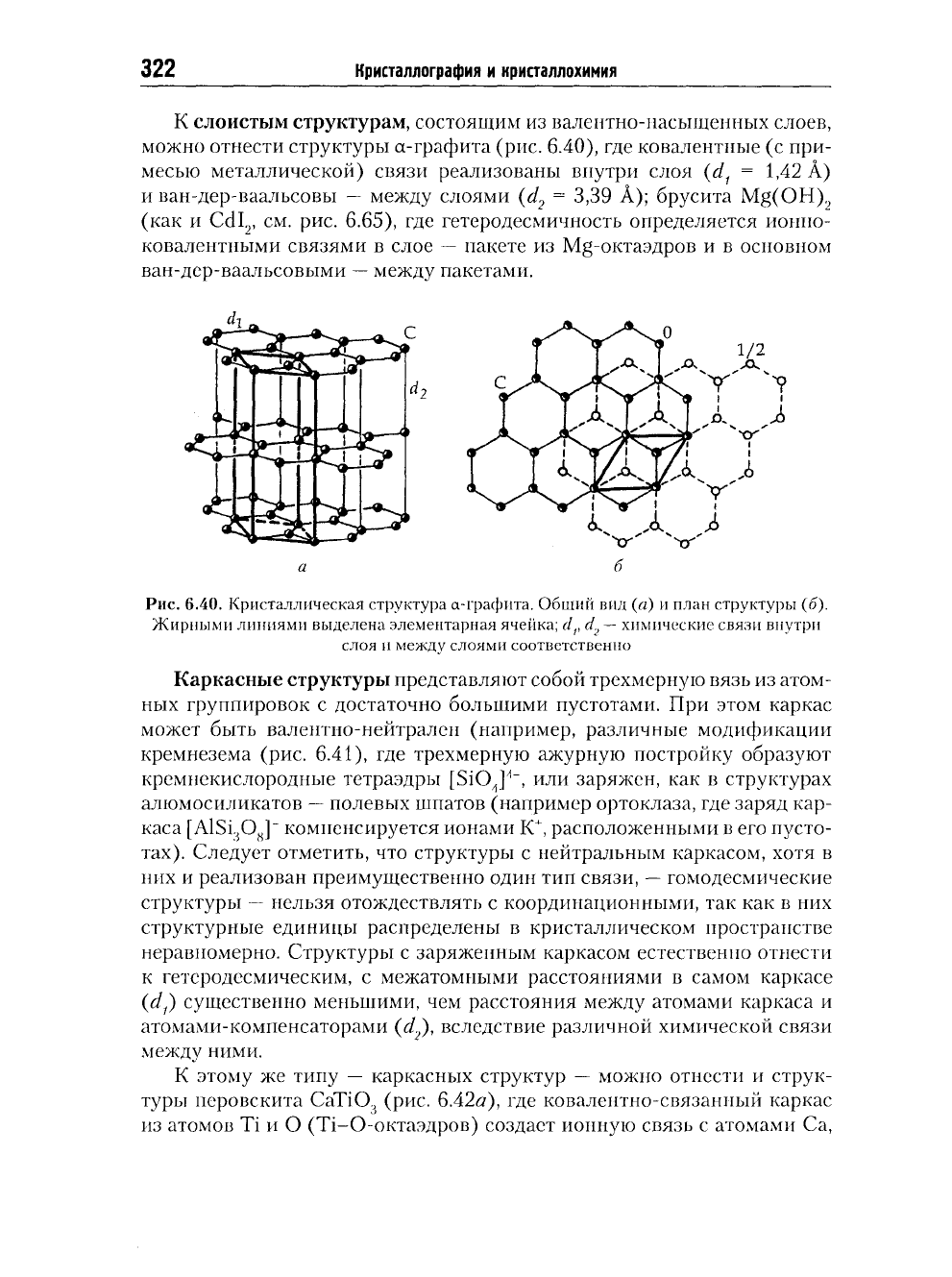
Цепочечные структуры
также могут состоять
как из
нейтральных,
так
и из
валентно-насыщенных цепочек. Примером первого типа явля-
ется структура селена (рис. 6.39а),
где
между атомами
Se,
выстроенными
в цепи, реализуется ковалентная связь
(d
1
= 2,32 А), а
между атомами
из
соседних цепочек — связи, близкие
к
ван-дер-ваальсовым
(d
2
= 3,46 А).
Ко второму типу можно отнести структуру NaHC0
3
, где водородные свя-
зи выстраивают карбонатные ионы (НС0
3
)~
в
цепи
(рис. 6.396),
связь
между которыми осуществляется через ионы
Na
+
.
Такой
же
структур-
ный мотив наблюдается
и в
обычных силикатах цепочечного строения
(см.
параграф
6.10.4).
а
6
Рис.
6.39.
Цепочечная структура селена (я). Черным цветом выделена цепочка
из атомов
Se.
Цепи (НСО^)
в
структуре
NaHCO.j
(б) (1
— водородная связь)
1 1
- 98.
322
Кристаллография
и
кристаллохимия
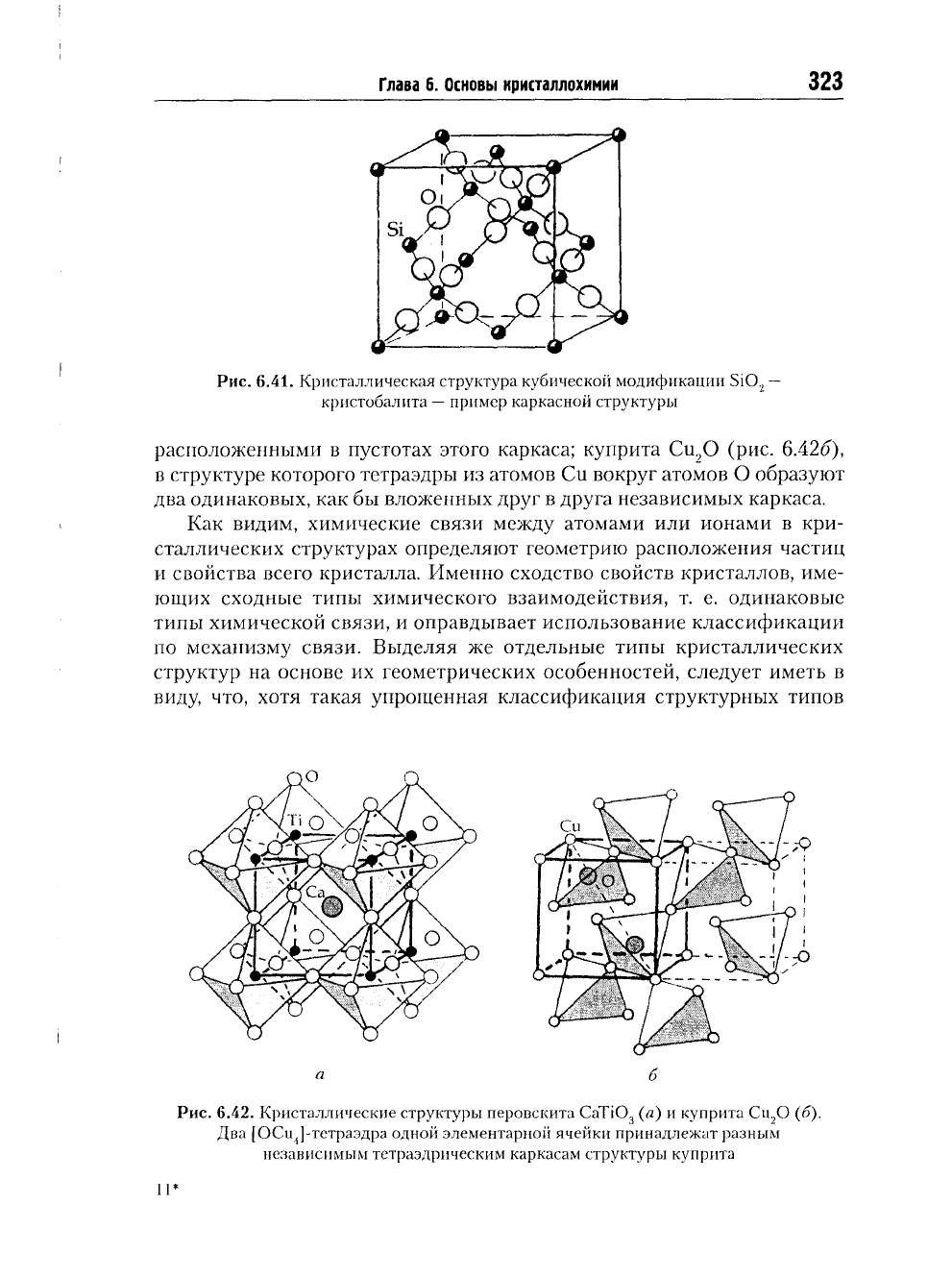
К слоистым структурам, состоящим
из
валентно-насыщенных слоев,
можно отнести структуры а-графита (рис.
6.40), где
ковалентпые
(с
при-
месью металлической) связи реализованы внутри слоя
(d
1
= 1,42 А)
и ван-дер-ваальсовы — между слоями
(d
2
= 3,39 А);
брусита Mg(OH)
2
(как
и
Cdl
2
,
см. рис. 6.65), где
гетеродесмичность определяется ионно-
ковалентными связями
в
слое — пакете
из
Mg-октаэдров
и в
основном
ван-дер-ваальсовыми
—
между пакетами.
Рис.
6.40.
Кристаллическая структура а-графита. Общий
вид (а) и
план структуры
(б).
Жирными линиями выделена элементарная ячейка;
d
v
d.j
—
химические связи внутри
слоя
и
между слоями соответственно
Каркасные структуры представляют собой трехмерную вязь
из
атом-
ных группировок
с
достаточно большими пустотами.
При
этом каркас
может быть валентно-нейтрален (например, различные модификации
кремнезема
(рис. 6.41), где
трехмерную ажурную постройку образуют
кремнекислородные тетраэдры [SiOJ'
1-
,
или
заряжен,
как в
структурах
алюмосиликатов
—
полевых шпатов (например ортоклаза,
где
заряд кар-
каса
[AlSLjOJ
-
компенсируется ионами К*, расположенными
в его
пусто-
тах).
Следует отметить,
что
структуры
с
нейтральным каркасом, хотя
в
них
и
реализован преимущественно один
тип
связи, — гомодесмические
структуры — нельзя отождествлять
с
координационными,
так как в них
структурные единицы распределены
в
кристаллическом пространстве
неравномерно. Структуры
с
заряженным каркасом естественно отнести
к гетеродесмическим,
с
межатомными расстояниями
в
самом каркасе
(d,)
существенно меньшими,
чем
расстояния между атомами каркаса
и
атомами-компенсаторами
(d
2
),
вследствие различной химической связи
между ними.
К этому
же
типу — каркасных структур — можно отнести
и
струк-
туры перовскита
CaTiO.^
(рис.
6.42а),
где
ковалентно-связанный каркас
из атомов
Ti и О
(Ti-O-октаэдров) создает ионную связь
с
атомами
Са,
Глава б. Основы кристаллохимии
323
Рис.
6.41. Кристаллическая структура кубической модификации
SiO,
2
—
кристобалита
—
пример каркасной структуры
расположенными в пустотах этого каркаса; куприта
Си.,
О (рис.
6.426),
в структуре которого тетраэдры из атомов Си вокруг атомов О образуют
два одинаковых, как бы вложенных друг в друга независимых каркаса.
Как видим, химические связи между атомами или ионами в кри-
сталлических структурах определяют геометрию расположения частиц
и свойства всего кристалла. Именно сходство свойств кристаллов, име-
ющих сходные типы химического взаимодействия, т. е. одинаковые
типы химической связи, и оправдывает использование классификации
по механизму связи. Выделяя же отдельные типы кристаллических
структур на основе их геометрических особенностей, следует иметь в
виду, что, хотя такая упрощенная классификация структурных типов
Рис.
6.42. Кристаллические структуры перовскита СаТЮ
3
(я) и куприта Cu
2
0 (б).
Два [OCuJ-тетраэдра одной элементарной ячейки принадлежат разным
независимым тетраэдрическим каркасам структуры куприта

324 Кристаллография и кристаллохимия
удобна и полезна, все же она не может охватить все многообразие струк-
тур известных к настоящему времени химических соединений.
6.6. ПЛОТНЕЙШИЕ ШАРОВЫЕ УПАКОВКИ В КРИСТАЛЛАХ
При изучении строения многих кристаллических веществ невольно
возникают вопросы: «Чем объяснить возникновение той или иной струк-
туры кристаллов? Почему структура одних кристаллов так разительно
отличается от структуры других?» Физик объяснит данное расположение
атомов тем, что иное их расположение привело бы к большей свободной
энергии. Действительно, закон природы связывает устойчивость струк-
тур кристаллов, и не только кристаллов, а вообще вещества в любом со-
стоянии, с минимальной свободной энергией. И кристалл в этом слу-
чае можно сравнивать с мячиком, брошенным со склона горы, который
катится вниз до тех пор, пока не достигнет стабильности положения,
т. е. того момента, когда силы тяжести и силы гравитационного взаимо-
действия между Землей и телом уравновесятся. Так и кристалл будет
иметь то распределение образующих его атомов, при котором силы вза-
имодействия между частицами уравновесятся. Именно такой структу-
ре и будет соответствовать минимальная свободная энергия кристалла.
Зафиксировав положения атомов, мы получим геометрическую модель
структуры кристалла, в которой координация того или иного элемента,
а следовательно, и геометрия самой структуры
—
ее геометрический ха-
рактер, симметрия — зависят от типа реализованных в ней химических
связей.
Симметрия структур кристаллов описывается одной из 230 федо-
ровских (пространственных) групп. Причем в современной кристалло-
графии широко известно важное эмпирическое наблюдение, касающе-
еся неравномерного распределения структур кристаллических веществ
между 230 пространственными группами. Действительно, всего девять
пространственных групп описывают около 40 % всех кристаллических
структур минералов и неорганических соединений, тогда как для описа-
ния остальных 60 % необходима почти сотня пространственных групп.
Еще 100 пространственных групп встречаются очень редко и описывают
примерно 0,2 % кристаллических структур, а около 20 вообще не реали-
зованы в известных к настоящему времени кристаллических структурах.
Одна из наиболее успешных попыток объяснения этого факта связана
с широко известной концепцией плотнейших упаковок сферических ато-
мов или ионов определенного радиуса. Хотя теория плотнейших упако-
вок разработана математиками, ее использование существенно упрощает
симметрийный анализ и описание геометрии расположения атомов или
ионов в кристаллических структурах многих веществ.

Глава
6.
Основы кристаллохимии
325
Например,
в
случае
с
ненаправленной
и
ненасыщаемой металличе-
ской связью атомы, подчиняясь геометрическому принципу максималь-
ного заполнения кристаллического пространства, располагаются
в
боль-
шинстве случаев плотнейшим образом.
Это
позволяет, представив атомы
в виде несжимаемых шаров одинакового размера, использовать теорию
плотнейших упаковок
для
описания многих кристаллических структур.
6.6.1.
Теория плотнейших упановок
Исторически первой была замечена укладка квадратных слоев,
т. е.
слоев тетрагональной симметрии
(рис.
6.43а). Укладывая друг
на
друга
эти слои
так,
чтобы шары каждого следующего слоя попадали
в
лунки
между четырьмя шарами предыдущего слоя, получим максимально плот-
ную упаковку шаров,
т. е.
будет достигнут максимальный коэффициент
заполнения пространства одинаковыми шарами —
74,05 %
(рис.
6.436).
Нетрудно убедиться
в
том,
что
каждый
шар в
этом случае будет касаться
12
соседних шаров: четыре шара
в
слое, четыре сверху
и
четыре снизу.
Такая упаковка имеет кубическую симметрию,
и в
выделенной
в ней
эле-
ментарной ячейке шары будут располагаться
по
узлам гранецентриро-
ванпой решетки Браве (рис. 6.43в
и
6.37а).
Такой способ плотнейшей укладки шаров долгое время считался
единственным,
что на
первый взгляд подтверждалось равенством числа
шаров
и
лунок
в
каждом слое (каждый
шар
окружен четырьмя лунками,
каждая лунка
—
четырьмя шарами).
При
этом шары каждого квадратно-
го слоя заполняют все лунки предыдущего,
и,
казалось бы, никаких иных
вариантов укладки шаров одинакового размера предложить нельзя.
Z
а
б а
Рис.
6.43.
Плотнейшая шаровая укладка
из
квадратных слоев:
а
— изолированный
квадратный шаровой слой (соотношение числа шаров
и
лунок
—1:1);
б
—
квадратные слои образуют плотнейшую упаковку;
а
—
шары плотнейшей упаковки служат узлами
кубической гранецентрированной
(F)
решетки Браве

326
Кристаллография и кристаллохимия
Однако более 100 лет назад англичанин В. Барлоу, сориентировав
кубическую ячейку плотнейшей упаковки вдоль одной из осей 3-го по-
рядка (рис. 6.44а), выделил в ней слои иной конфигурации и симметрии,
расположенные перпендикулярно этой оси (рис.
6.446).
В таких слоях
каждый шар оказался окруженным не четырьмя, а шестью аналогичны-
ми шарами (рис. 6.44в). Это максимальное число (6) касаний характе-
ризует плотноупакованный — плотнейший — слой, в котором шарами
(кругами в двухмерном случае) заполнено приблизительно 90,7 % двух-
мерного пространства. Симметрия слоя такой конфигурации оказалась
гексагональной.
Каждый шар в этом слое (назовем его слоем А) (рис. 6.44в) окружен
шестью лунками, каждая из которых в свою очередь образована тремя
шарами этого же слоя. Таким образом, число лунок в слое в два раза пре-
вышает число шаров. Однако кристалл
—
это трехмерная постройка, где
один плотноупакованный слой наложен на другой таким образом, что
каждый шар вышележащего слоя оказывается в треугольной лунке ни-
жележащего слоя. При этом не все шесть лунок предыдущего слоя А ока-
жутся заполненными шарами второго слоя (В), а только половина (рас-
положить шары в каждой лунке не позволит размер шаров) (рис. 6.44«).
Следует отметить, что, пока мы рассматриваем один слой, лунки В и С,
по сути, не различаются, т. е. в принципе неважно, какие из них будут
заполнены — В или С. В результате такого заполнения лунок получим
второй слой (например, В), геометрически совершенно эквивалентный
нижележащему (А).
Рис.
6.44. Разделение плотнейшей укладки шаров (а) на плотнейшие слои (б),
перпендикулярные оси 3-го порядка гексагональной симметрии.
В изолированном плотнейшем слое (в) каждый шар окружен
шестью лунками (В и С), а так как каждая лунка образована
тремя шарами, то соотношение числа шаров и лунок 1 : 2
а
б
в

Глава
6.
Основы кристаллохимии
327
Рис.
6.45.
Шары
2-го
слоя заполняют лишь половину лунок предыдущего
плотноупакованного слоя.
При
этом образуются половина сквозных
(1)
и половина несквозных
(2)
лунок
Однако
при
наложении шаров второго слоя одни лунки
(1)
оказыва-
ются сквозными
(т. е. над
ними
нет
шаров второго слоя
В),
другие
(2)
—
несквозными (прикрыты шарами второго слоя)
(рис. 6.45). Это
создает
два варианта наложения шаров третьего слоя.
В
первом случае заполне-
ние несквозных лунок
(2)
приведет
к
тому,
что уже
третий слой располо-
жится
над
первым, четвертый
—
над
вторым
и т. д. В
результате получен-
ная упаковка плотнейших слоев окажется двухслойной
и
запишется
как
чередование двух букв
АВ АВ АВ... —
слоев
А и В (рис. 6.46). Во
втором
случае если шары третьего слоя
(С)
укладывать
в
сквозные лунки
(1), то
повторение наступит
на
четвертом слое,
и
закономерность чередования
уже трех независимых слоев
в
этом случае
в
буквенном обозначении
за-
пишется
как ABC ABC...
(рис.
6.47).
В первом случае
на
период повторяемости упаковки будут при-
ходиться
два
слоя
А и В
(независимый пакет
АВ), в
результате чего
возникает двухслойная плотнейшая упаковка гексагональной симмет-
рии —
АВ АВ АВ... (рис. 6.46).
Отсюда
и ее
название
—
гексагональная
плотнейшая упаковка (ГПУ).
Во
втором случае формируется упаковка
из
трех слоев
А, В и С
кубической симметрии (независимый пакет
ABC) —
кубическая плотнейшая упаковка
(КПУ)
—
ABC ABC... (рис. 6.47).
Сле-
дует отметить,
что
если
в
гексагональной упаковке перпендикулярно
единственному направлению осей
3-го
порядка можно выделить лишь
одну систему параллельных плотноупакованных слоев,
то в
кубической
плотнейшей упаковке
с
четырьмя направлениями осей
3
таких систем
плотнейших слоев будет четыре
и
каждая
из них
окажется перпендику-
лярна одному
из
направлений осей
3-го
порядка.
Каждый слой гексагональной упаковки расположен между одинако-
выми слоями (слой
А —
между слоями
В,
слой
В
—
между слоями
А), т. е.
лежит
в
плоскости симметрии, связывающей верхний
и
нижний слои.
В кубической упаковке каждый слой расположен между двумя разны-
ми слоями (слой
А
— между слоями
В и С,
слой
В —
между слоями
А и
Сит. д.). Таким образом, верхний
и
нижний соседние слои относитель-
но центрального
в
двухслойной плотнейшей упаковке располагаются
328
Кристаллография и кристаллохимия
а б
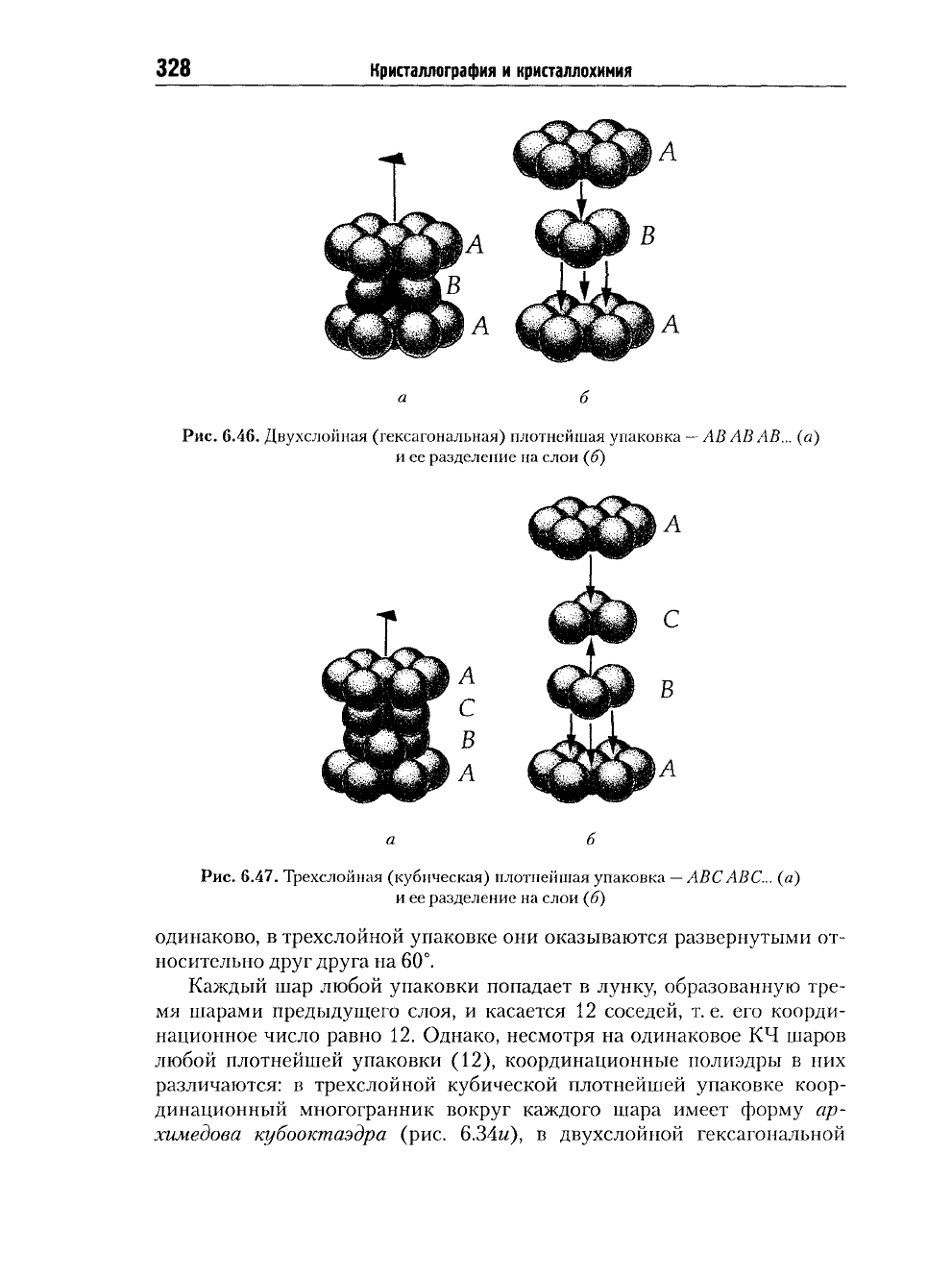
Рис.
6.46. Двухслойная (гексагональная) плотнейшая упаковка
—
АВ АВ АВ... (я)
и ее разделение на слои (б)
а б
Рис.
6.47. Трехслойная (кубическая) плотнейшая упаковка
—
ABC
ABC...
(я)
и ее разделение на слои (б)
одинаково, в трехслойной упаковке они оказываются развернутыми от-
носительно друг друга на 60°.
Каждый шар любой упаковки попадает в лунку, образованную тре-
мя шарами предыдущего слоя, и касается 12 соседей, т. е. его коорди-
национное число равно 12. Однако, несмотря на одинаковое КЧ шаров
любой плотнейшей упаковки (12), координационные полиэдры в них
различаются: в трехслойной кубической плотнейшей упаковке коор-
динационный многогранник вокруг каждого шара имеет форму ар-
химедова кубооктаэдра (рис. 6.34и), в двухслойной гексагональной

Глава 6. Основы кристаллохимии
329
упаковке — форму гексагонального аналога кубооктаэдра (рис.
6.34к)
с единственной осью 3-го порядка. Во всех случаях коэффициент запол-
нения пространства одинаков и равен
74,05
%. Различные закономерные
комбинации трех слоев — А, В и С — позволяют получить бесконечное
множество многослойных упаковок симметрии (например, четырех-
слойную —
ABAC...,
шестислойную — АВСАСВ... и т. п.) с тем же мак-
симальным коэффициентом заполнения пространства и координацион-
ным числом каждого шара 12. При этом существенно то, что симметрия
всех таким образом полученных упаковок описывается только восе-
мью пространственными группами, семь из которых — гексагональные
б
(Р—тс,
PG
s
mc,
Р6т2, РЗт, РЗт, R3m, R3m) и лишь одна (трехслой-
m _
пая)
—
кубическая ( РгпЗпг).
6.6.2.
Симметрия плотноупакованного слоя
Прежде чем определять симметрию плотнейших упаковок, следует
выяснить, какой точечной группой описывается симметрия одного изо-
лированного плотноупакованного слоя. Координационное число каждого
шара в слое равно б. Это наиболее плотная укладка шаров. Нетрудно уви-
деть (рис.
6.48),
что симметрия двухмерной упаковки шаров одинакового
размера описывается голоэдрической гексагональной пространственной
п
6
группой
F
~
mm
•
Через центр каждого шара проходит ось 6-го порядка,
перпендикулярная плотноупакованному слою. В центрах треугольных
лунок располагаются оси 3-го порядка, а между каждой парой шаров
локализована ось 2-го порядка. Убеждаемся в справедливости правила,
что взаимодействие оси п-го порядка с перпепдикулярушм к ней трансля-
ционным вектором приводит к появлению оси того же порядка в центре
п-уголышка, построенного на этой трансляции в сторону рассматри-
ваемого вращения. Действительно, оси 6
в
оказываются в центрах всех
шестиугольников, оси 3 и 2, являющиеся подгруппами оси 6, — в цен-
трах треугольников и двуугольников (серединах трансляций) соответ-
ственно.
Следует обратить внимание на то, что в точечных группах все элемен-
ты симметрии пересекаются в одной точке. В бесконечных же построй-
ках (в частности, в кристаллических структурах) присутствует бесконеч-
ное число одинаковых параллельных элементов симметрии, что связано
с присутствием в них трансляционных векторов.
Выделив по осям 6-го порядка элементарную ячейку (с параметрами
а = b * с, а = (3 = 90°, у
=
120°), обозначим координатные (X, Y, U) и рас-
положенные к ним под углами 30° (а/2) диагональные (апофемальные)
направления.
