Егоров-Тисменко Ю.К. Кристаллография и кристаллохимия

Подождите немного. Документ загружается.

330

Кристаллография и кристаллохимия

Рис.

6.48. К определению симметрии плотноупакованного слоя

Далее легко находим координатные плоскости

—

, т , т

и т

, каж-

дая из которых перпендикулярна одному из координатных направле-

ний

. При этом плоскость т

проходит через центры тяжести всех шаров

плотноупакованного слоя. Обнаруживаем и апофемальные плоскости

), расположенные перпендикулярно диагональным особым направ-

лениям выделенной элементарной ячейки и составляющие с координат-

иыми плоскостями углы в 30°. Отсутствие позиций с симметрией "~

тт

кроме как в вершинах элементарной ячейки, говорит о ее примитивно-

сти

—

Р.

В итоге получаем голоэдрическую симморфную (см. параграф

6.2.5)

пространственную группу ^~

тт

- Обращаем внимание на то, что пло-

скости симметрии (координатные и апофемальные) являются порожда-

ющими элементами симметрии, а оси симметрии

—

порожденными. Дей-

ствительно:

•

= З

, т

•

= 6

, т

•

= 2

СО'

30" 90

б.б.З. Симметрия двухслойной гексагональной плотнейшей упаковки

При воссоздании двухслойной (гексагональной) плотнейшей упа-

ковки удобно обозначать кружками лишь центры тяжести шаров с указа-

нием соответствующих высот в долях параметра с элементарной ячейки:

Следует иметь в виду, что плоскости, проходящие через координатные на-

правления, являются апофемальиыми, а проходящие через апофемальные — ко-

ординатными, так как особым направлением является не сама плоскость, а нор-

маль к пей.

Глава б. Основы кристаллохимии

331

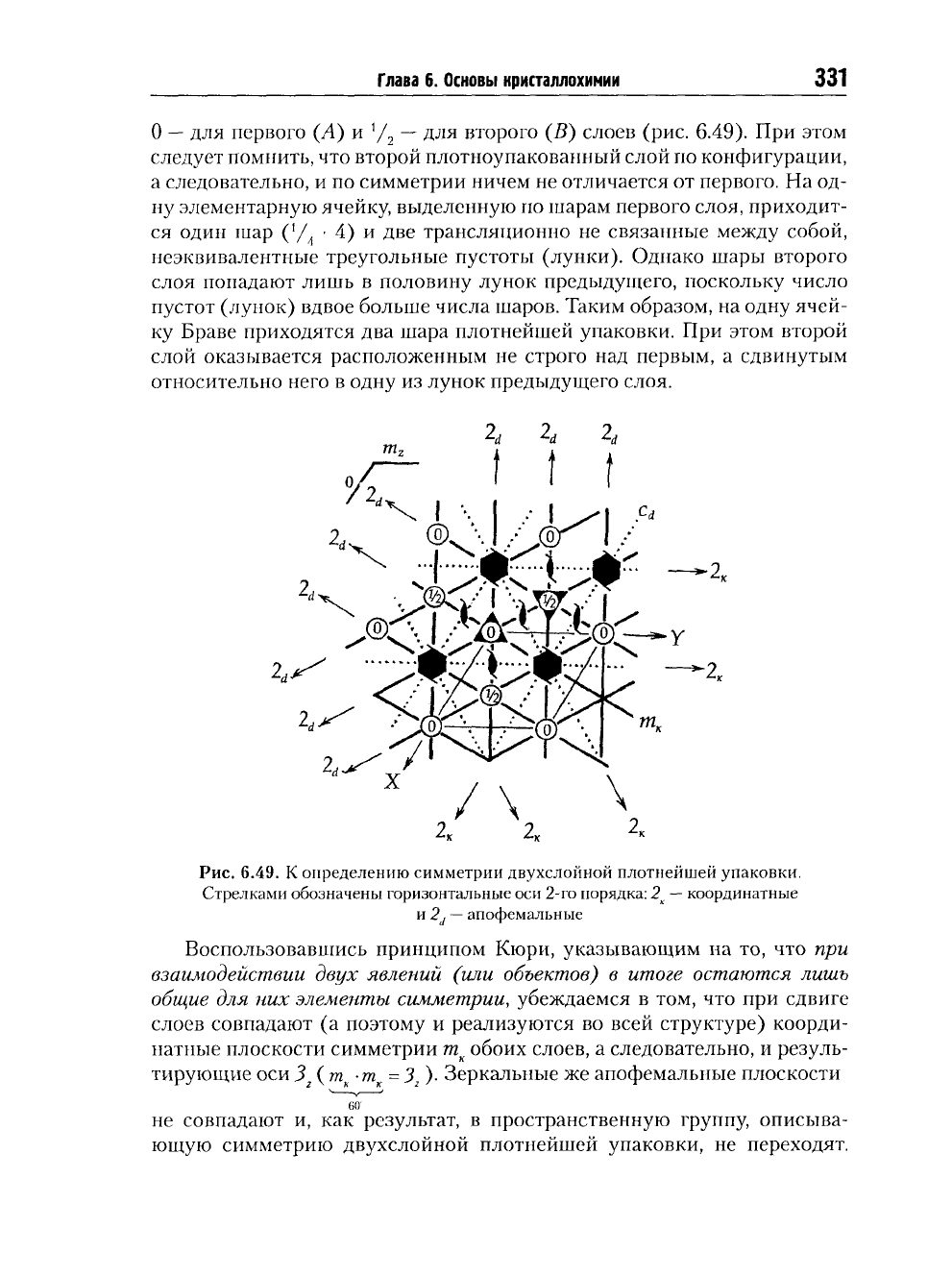
О —

для первого (А) и

— для второго (В) слоев (рис.

6.49).

При этом

следует помнить, что второй плотноупакованный слой по конфигурации,

а следовательно, и по симметрии ничем не отличается от первого. На од-

ну элементарную ячейку, выделенную по шарам первого слоя, приходит-

ся один шар ('/ • 4) и две трансляционно не связанные между собой,

неэквивалентные треугольные пустоты (лунки). Однако шары второго

слоя попадают лишь в половину лунок предыдущего, поскольку число

пустот (лунок) вдвое больше числа шаров. Таким образом, на одну ячей-

ку Браве приходятся два шара плотнейшей упаковки. При этом второй

слой оказывается расположенным не строго над первым, а сдвинутым

относительно него в одну из лунок предыдущего слоя.

Рис. 6.49. К определению симметрии двухслойной плотнейшей упаковки.

Стрелками обозначены горизонтальные оси 2-го порядка: 2

—

координатные

и 2j — апофемальные

Воспользовавшись принципом Кюри, указывающим на то, что при

взаимодействии двух явлений (или объектов) в итоге остаются лишь

общие для них элементы симметрии, убеждаемся в том, что при сдвиге

слоев совпадают (а поэтому и реализуются во всей структуре) коорди-

натные плоскости симметрии т

обоих слоев, а следовательно, и резуль-

тирующие оси 3 ( т

)• Зеркальные же апофемальные плоскости

60'

не совпадают и, как результат, в пространственную группу, описыва-

ющую симметрию двухслойной плотнейшей упаковки, не переходят.

332

Кристаллография

кристаллохимия

Однако вместо

них

появляются такой

же

ориентации плоскости сколь-

зящего отражения

связывающие шары

из

разных (первого

второго)

слоев. Взаимодействие

же

координатных

апофемальных плоскостей,

расположенных

под

разными углами одна

другой, вновь обусловит

по-

явление осей

6-го и 2-го

порядков,

но уже

винтовых (рис.

6.49).

Записав

для каждой порождающей плоскости симметрии составляющие

ее

опе-

рации, получим:

(=3-2

где

-1

(=^р\

=2;

•

с,

•

i.=3

(в

составе

оси

во

Горизонтальные зеркальные плоскости симметрии, проходящие

че-

рез каждый плотноупакованный слой, хотя

и не

совпали,

но

оказались

расположенными через полтрансляции вдоль координатной

оси Z.

И поскольку плотнейшая упаковка двухслойная, этим плоскостям под-

чиняется расположение всех слоев плотноупакованного пространства.

В итоге получаем также голоэдрическую,

но уже

несимморфную про-

странственную группу

примитивной решеткой Браве

—

Р—тс,

раз-

вернутый символ которой, помимо вертикальных осей симметрии, будет

содержать

горизонтальные

оси 2-го

порядка, возникшие

как

результат

взаимодействия горизонтальной плоскости

вертикальными плоско-

стями

т и с,

—

Р-1- .

' т т с Q

Построим график пространственной группы Р—тс

определим

характеристики правильной системы точек, занимаемой шарами двух-

слойной плотнейшей упаковки.

Прежде

чем

начать построение графика пространственной группы

Р—тс,

следует решить вопрос

выборе

в ней

начала координат,

для

чего

необходимо найти самую симметричную

самую неподвижную точку

(точку

минимальным количеством степеней свободы). Рассмотрим

все принципиально разные

по

симметрии позиции данной простран-

ственной группы, учитывая

при

этом лишь макроэлементы симметрии,

т.

е.

элементы симметрии, фиксирующие точку

и не

размножающие

ее

(помним,

что

трансляционные элементы симметрии точку

ие

фиксиру-

ют

и она

ведет себя относительно этих элементов

как

точка общего

по-

ложения (см. рис.

6.28)).

Симметрия точки пересечения

оси 3,

входя-

щей

состав

оси 6

}

= 3

•

горизонтальной плоскости

описывается

Глава

6. Основы кристаллохимии

333

точечной группой 6т2

=—т

Такой же точечной симметрией обладает

и позиция на самостоятельной оси 3-го порядка.

Обратим внимание на то, что в точечных группах безразлично, какая

тройка вертикальных плоскостей симметрии принята за порождающую:

координатных или диагональных. При описании симметрии кристалли-

ческих структур такой выбор небезразличен, поскольку координатные

направления выбираются по минимальным трансляционным векторам,

а они могут совпадать либо с нормалями к плоскостям, либо с осями 2-го

порядка. В результате вместо одной точечной группы бт2 появляются

две подчиненные ей пространственные группы

Р6т2

и P62m- Различия

в положении исходных плоскостей симметрии хорошо видны на графи-

ках пространственных групп Р31т и Р3т1, являющихся подгруппами

пространственной группы Рбтт (рис.

6.50).

Пространственная группа

Р6т2

не содержит центра инверсии (7),

так же как не содержит центра инверсии инверсионная ось 4. В то же

время ось 3

3-1 центр инверсии содержит. Помним, что центр инвер-

сии возникает при взаимодействии оси 2 с перпендикулярной ей плоскос-

тью симметрии (2 -т

= 1). В нашем же случае в пространственной группе

p^l-mc ось 6

содержит в качестве подгруппы винтовую ось 2

которая,

взаимодействуя с перпендикулярной плоскостью пг, обусловливает по-

явление центра инверсии, перемещенного из точки пересечения оси 2

1 •••

на половину трансляционного вектора t

=-t

. Таким образом, центр

„ 1 -

инверсии оказывается отстоящим от горизонтальной плоскости т

на -Г .

Убеждаемся в том, что симметрия позиции, совпадающей с 1 , описыва-

ется точечной группой Зт.

В результате в группе

Р—тс

имеем три позиции с одинаковой вели-

те

чиной симметрии 12 (т. е. с одинаковой размножающей способностью):

Рбтт

Р3т1 РЗЪп

Рис.

6.50. Графики гемиморфной пространственной группы Рбтт

ее подгрупп Р3т1 и Р31т

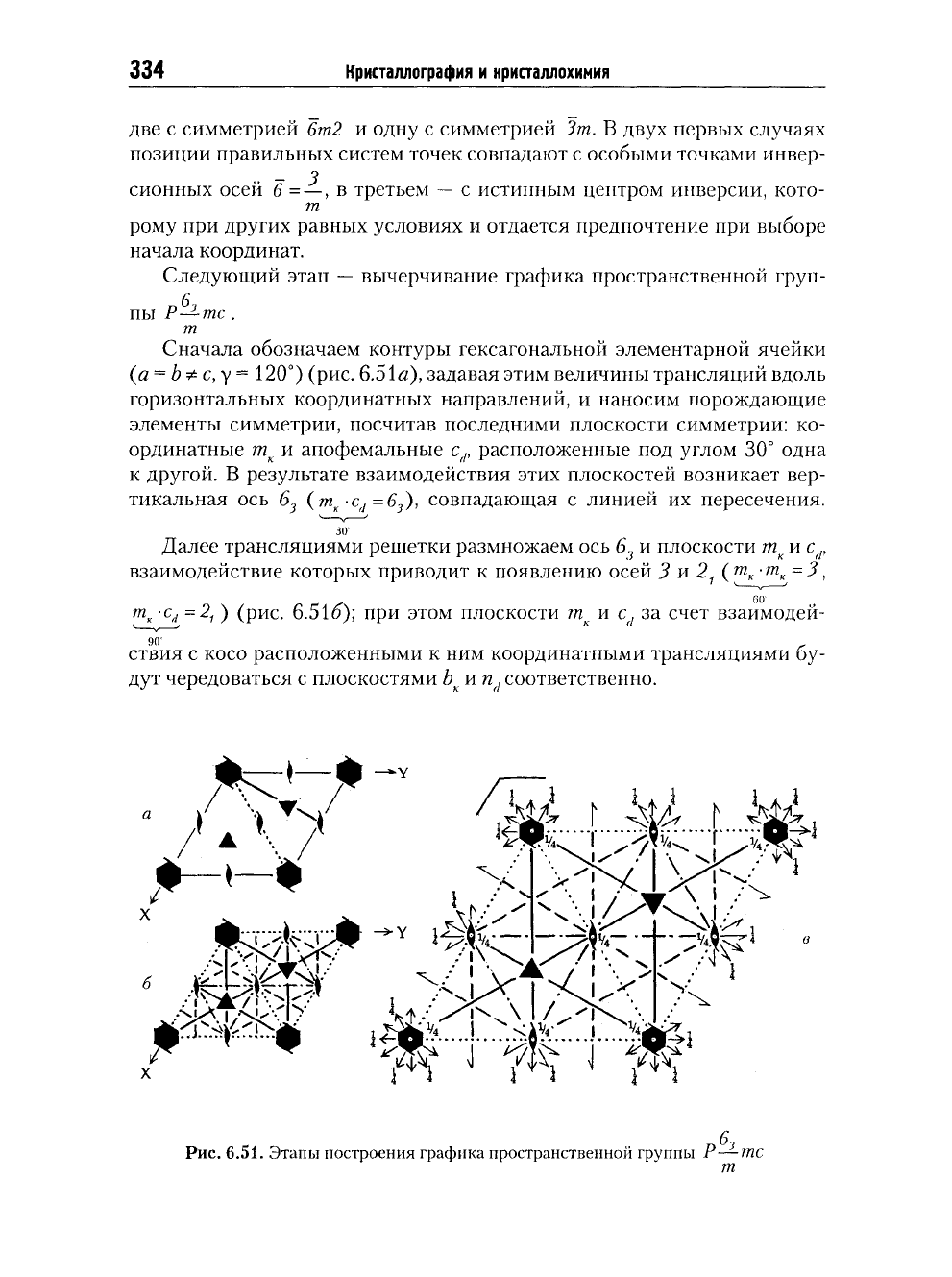
334

Кристаллография

кристаллохимия

две

симметрией

6т2 и

одну

симметрией

Зт. В

двух первых случаях

позиции правильных систем точек совпадают

особыми точками инвер-

- 3

сионных осей

—,

третьем —

истинным центром инверсии, кото-

рому

при

других равных условиях

отдается предпочтение

при

выборе

начала координат.

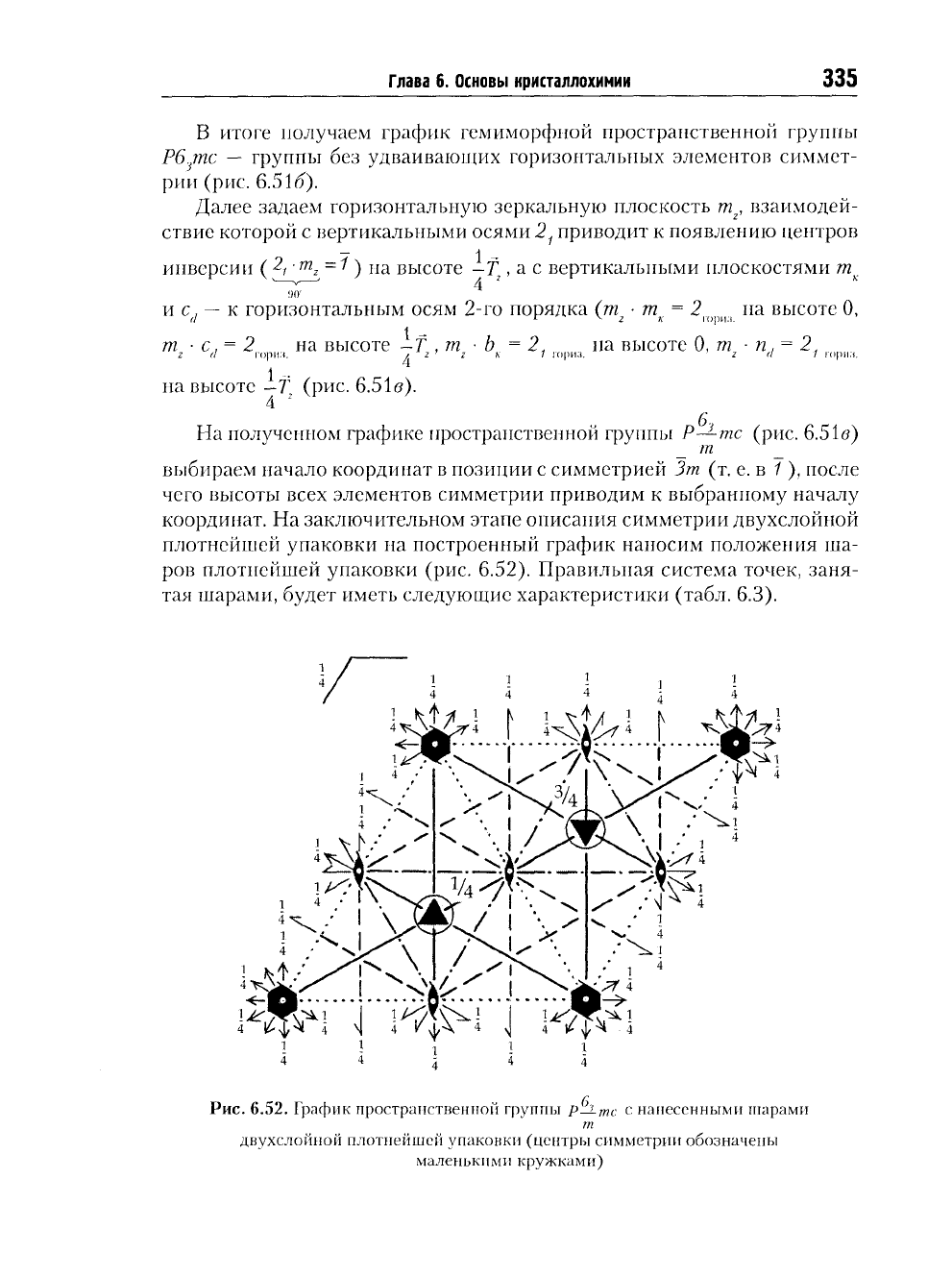
Следующий этап — вычерчивание графика пространственной труп-

ов

пы Р—тс.

Сначала обозначаем контуры гексагональной элементарной ячейки

(а =

с, у =

120°) (рис. 6.51а), задавая этим величины трансляций вдоль

горизонтальных координатных направлений,

наносим порождающие

элементы симметрии, посчитав последними плоскости симметрии:

ко-

ординатные

апофемальные

г1

расположенные

под

углом

30°

одна

к другой.

результате взаимодействия этих плоскостей возникает вер-

тикальная

ось 6

-Cj=6

совпадающая

линией

их

пересечения.

30*

Далее трансляциями решетки размножаем

ось 6

плоскости

и с

взаимодействие которых приводит

появлению осей

3 и 2

(

=3,

60'

-c

)

(рис. 6.51

о);

при

этом плоскости

и с

за

счет взаимодей-

ствия

косо расположенными

к ним

координатными трансляциями

бу-

дут чередоваться

плоскостями

и п

соответственно.

Глава

Основы кристаллохимии

335

В итоге получаем график гемиморфной пространственной группы

Рб./пс

—

группы

без

удваивающих горизонтальных элементов симмет-

рии (рис.

6.516).

Далее задаем горизонтальную зеркальную плоскость

взаимодей-

ствие которой

вертикальными осями

приводит

появлению центров

—

инверсии

( 2, •т

-1)

иа

высоте

-Т

, а с

вертикальными плоскостями

—

горизонтальным осям

2-го

порядка (тп

•

пг

= 2

иа

высоте

О,

тп

• с, = 2 на

высоте

—

тп

• b = 2. па

высоте

тп

• п, = 2,

г а

гори:).

^ 2 ' z к 1

гори.ч.

г п 1

I"O|IM:I,

на высоте

-Т

(рис. 6.51в).

На полученном графике пространственной группы Р—тс (рис. 6.51в)

т _

выбираем начало координат

позиции

симметрией

Зт (т. е. в 1 ),

после

чего высоты всех элементов симметрии приводим

выбранному началу

координат.

На

заключительном этапе описания симметрии двухслойной

плотнейшей упаковки

на

построенный график наносим положения

ша-

ров плотнейшей упаковки

(рис. 6.52).

Правильная система точек, заня-

тая шарами, будет иметь следующие характеристики (табл.

6.3).

Рис.

6.52.

График пространственной группы

pli-mc с

нанесенными шарами

двухслойной

плотнейшей упаковки (центры симметрии обозначены

маленькими

кружками)

336

Кристаллография

кристаллохимия

Таблица

6.3

Характеристики правильной системы точек, занимаемой

шарами двухслойной плотнейшей упаковки

Симметрия Величина

Число степеней Кратность Координаты

позиции симметрии свободы

6т2

24:

12 = 2

11 123

334'334

При этом позиции

симметрией

6т2 (001/4) и Зт

(ООО) остаются

вакантны.

6.6.4.

Симметрия трехслойной (кубической) плотнейшей упаковки

От двухслойной, гексагональной плотнейшей упаковки

(АВ) к

трех-

слойной, кубической легко перейти, расположив шары третьего слоя

(С)

над лунками

(1)

(см. рис.

6.45), еще не

занятыми шарами второго слоя

(В)

(рис.

6.53).

Выделив элементарную ячейку

по

горизонтальным трансля-

циям, убеждаемся,

что в

вертикальном направлении слои Л,

В и

С отстоят

друг

от

друга

на -if.. В

такой ячейке, помимо координатных трансляций,

возникает дополнительный трансляционный вектор

(Т

располо-

женный вдоль длинной телесной диагонали ячейки:

—>

—»

—>

А,

указывающий

на

дважды объемноцентрированный (ромбоэдрический)

тип ячейки Браве

—

Легко увидеть,

что

шары всех трех уровней располагаются

на по-

воротных осях

3-го

порядка,

центры тяжести всех шаров совпадают

центрами инверсии. Кроме того, через

оси 3-го

порядка проходят коор-

динатные зеркальные плоскости.

итоге, рассматривая плотно упако-

ванное пространство

указанном ракурсе, получаем ромбоэдрическую

пространственную группу

R3m.

Однако, выделив вокруг какого-либо

шара

ближайших соседей (шесть

слое,

три

сверху

и три

снизу)

мысленно соединив

их

отрезками, получим многогранник (координа-

ционный полиэдр),

по

форме отвечающий архимедову кубооктаэдру

(рис.

6.54а).

Симметрия такого полиэдра описывается точечной группой

m3m

т.

е.

комбинацией элементов симметрии кубической голоэдрии, содержа-

щей

три оси 4-го

порядка, четыре

оси 3-го

порядка

и т. д.

Сориентировав

кубооктаэдр (рис.

6.54-5) и

соответственно кубическую плотнейшую упа-

ковку

по

одной

из

осей

4-го

порядка, увидим,

что в

таком плотноупако-

ванном пространстве можно выделить кубическую гранецентрированную

ячейку. Симметрия кубической F-ячейки оказывается выше ромбоэдриче-

Глава

Основы кристаллохимии

337

Рис.

6.53. К

определению симметрии трехслойной (кубической)

плотнейшей упаковки

ской

описывается симморфной пространственной группой

Fm3m

}

под-

группой которой будет

Ют.

Построив проекцию кубической /^-ячейки

на

координатную пло-

скость

ху

(рис.

6.55),

убеждаемся,

что в ней

присутствуют координатные

(т

)

диагональные

(т

г1

)

зеркальные плоскости симметрии

и,

следо-

вательно,

как

результат

их

взаимодействий присутствует

весь осевой

комплекс 2>L

ALAbL

. Развернутый международный символ получен-

ной пространственной группы будут иметь следующий

вид: F—3-.

m m

Начало координат

этой группе выбирается

самой высокосимметрич-

ной позиции, описываемой точечной группой

m3m

т. е. в

центре тяжести

одного

из

шаров плотнейшей упаковки.

Рис.

6.54.

Координационный полиэдр

виде кубооктаэдра,

ориентированный

по

осям

3-го (а) и 4-го (б)

порядков

338

Кристаллография и кристаллохимия

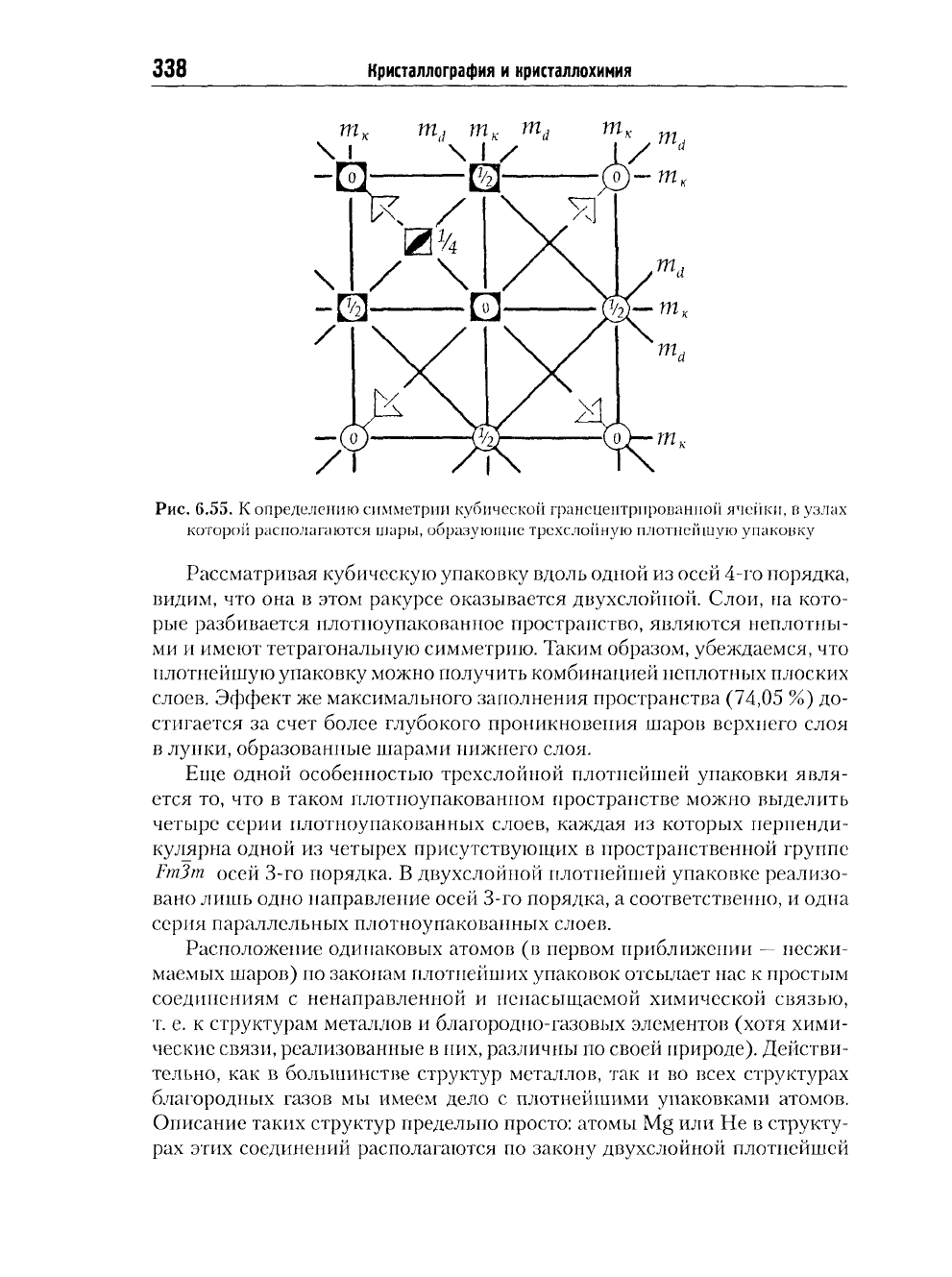
Рис. 6.55. К определению симметрии кубической грансцентрированной ячейки, в узлах

которой располагаются тары, образующие трехслойную плотнейшую упаковку

Рассматривая кубическую упаковку вдоль одной из осей 4-го порядка,

видим, что она в этом ракурсе оказывается двухслойной. Слои, на кото-

рые разбивается плотноупакованное пространство, являются неплотны-

ми и имеют тетрагональную симметрию. Таким образом, убеждаемся, что

плотнейшую упаковку можно получить комбинацией неплотных плоских

слоев. Эффект же максимального заполнения пространства

(74,05

%) до-

стигается за счет более глубокого проникновения шаров верхнего слоя

в лунки, образованные шарами нижнего слоя.

Еще одной особенностью трехслойной плотнейшей упаковки явля-

ется то, что в таком плотиоупакованпом пространстве можно выделить

четыре серии плотноупакованных слоев, каждая из которых перпенди-

кулярна одной из четырех присутствующих в пространственной группе

Fm3m осей 3-го порядка. В двухслойной плотнейшей упаковке реализо-

вано лишь одно направление осей 3-го порядка, а соответственно, и одна

серия параллельных плотноупакованных слоев.

Расположение одинаковых атомов (в первом приближении — несжи-

маемых шаров) по законам плотнейших упаковок отсылает нас к простым

соединениям с ненаправленной и ненасыщаемой химической связью,

т. е. к структурам металлов и благородно-газовых элементов (хотя хими-

ческие связи, реализованные в них, различны по своей природе). Действи-

тельно, как в большинстве структур металлов, так и во всех структурах

благородных газов мы имеем дело с плотнейшими упаковками атомов.

Описание таких структур предельно просто: атомы Mg или Не в структу-

рах этих соединений располагаются по закону двухслойной плотнейшей

Г лава

Основы кристаллохимии

339

упаковки (см. рис.

6.376),

атомы

Си

ИЛИ

АГ

образуют трехслойную кубиче-

скую упаковку (см. рис. 6.37а), атомы

—

четырехслойную упаковку.

Особенно изящной теория плотнейших упаковок шаров становится

при описании кристаллических структур

ионным типом связи.

Это

структуры также

ненаправленными

ненасыщаемыми связями,

од-

нако

ионных структурах приходится иметь дело

ионами

не

только

разных зарядов,

но и

разных размеров.

этом случае важен

тот

факт,

что плотнейшую упаковку

в них

создают

не

нейтральные атомы,

чаще

более крупные

по

размеру отрицательно заряженные частицы

—

анионы

(О

F~, CI", S

' и

др.), более мелкие катионы оказываются

пустотах

этой упаковки.

Следует отметить,

что о

«шарах, касающихся друг друга» можно

го-

ворить лишь

случае

кристаллами металлических

благородно-газо-

вых элементов, считая радиусами таких шаров (атомов) половины рас-

стояний между центрами

их

тяжести.

При

кулоновском взаимодействии

между атомами

ионных структурах катион, попав

окружение анио-

нов,

не

должен «болтаться»:

он

раздвигает своих соседей, разрежая

тем

самым

их

укладку

(см.

параграф

6.4.2).

Фактически речь

этом случае

может идти

не о

плотнейшей упаковке

строгом смысле слова,

т. е. не

о максимальном коэффициенте заполнения пространства,

лишь

рас-

положении центров тяжести более крупных

по

размеру ионов

по

закону

плотнейшей упаковки.

Итак,

учетом указанной оговорки принцип плотнейшей упаковки

вполне может быть применен

для

описания структур ионных соедине-

ний. Однако,

для

того чтобы

это

описание было достаточно полным,

не-

обходимо рассмотреть пустоты между шарами

плотнейших упаковках.

6.6.5. Пустоты

плотнейших упаковках.

Их расположение

симметрия

В многослойной модели

из

одинаковых атомов-шаров, пока

мы

рас-

сматриваем один слой, лунки

1 и 2 (см. рис. 6.45)

принципиально

не

отличаются друг

от

друга.

Но как

только накладывается второй слой,

лунки одного типа (например,

оказываются окруженными четырь-

мя соседними шарами,

лунки другого типа (например,

1) —

шестью.

Теперь

они

оказываются совершенно разными, поскольку

плотноупа-

кованном пространстве образуются

два

типа пустот:

первом случае,

соединив центры тяжести четырех шаров, получим тетраэдр — тетра-

эдрическую пустоту (рис. 6.56а,

б), во

втором получим пустоту

форме

октаэдра

—

октаэдрическую пустоту (рис. 6.56е,

г). Это

главные пустоты

плотнейшей упаковки; можно говорить

и о

тригональных (треугольных)

пустотах, расположенных

самом плотноупакованном слое (рис. 6.56Э),

и несколько условно

—

позициях

с КЧ = 2

(рис. 6.56е). Перечисленные