Динкель А.Д. Теория автоматического управления

Подождите немного. Документ загружается.

Знаменатель этой функции, приравненный к нулю, представляет со-

бой уравнение характеристической кривой разомкнутой системы:

0ω)(

jQ , (4.41)

а числитель, приравненный к нулю,— уравнение характеристической кри-

вой замкнутой системы:

0ω)(ω)(ω)(

зpp

+ jQjQjP . (4.42)

Если разомкнутая система устойчива, то, как показано выше, измене-

ние аргумента вектора

ω)(arg ∆

ω 0

nQ =

∞+≤≤

j . (4.43)

Заметим, что порядок характеристических уравнений разомкнутой

и замкнутой систем будет одинаковым в силу того, что порядок полинома

(р) практически всегда меньше порядка полинома Q

(p).

Если характеристическое уравнение замкнутой системы имеет m кор-

ней в правой полуплоскости комплексной плоскости, то изменение аргу-

мента вектора ω)(

jQ равно

)2(ω)(аrg ∆

mnQ −=j . (4.44)

Тогда изменение аргумента вектора

∞+≤≤ ω 0

ω)( аrg ∆ jF −

∞+≤≤ ω 0

ω)( аrg ∆

∞+≤≤ ω 0

ω)( аrg ∆

)2( mn −

n−

= –m π.(4.45)

Но замкнутая система будет устойчивой только при условии m = 0,

а следовательно, при условии, что изменение аргумента вектора

∞+≤≤ ω 0

ω)( аrg ∆ jF 0.

Это условие будет выполняться, если годограф вектора ω)( jF не ох-

ватывает начало координат, как это показано на рис. 4.12.

Рис. 4.12. Годограф вектора

ω)( jF

От годографа вектора )( ωjF , учитывая, что из (4.40)

1ω)(ω)(

−

jFjW

, (4.46)

можно перейти к годографу вектора ω)(

jW смещением начала координат

на рис. 4.13 в точку с координатами (–1, j0). Тогда начало вектора )( ωjF

сместится в точку с координатами (–1, j0), а годограф обращается в годо-

граф вектора

ω)(

, как это видно из рис. 4.13. Из этого следует, что

точка с координатами (–1, j0) не охватывается амплитудно-частотной ха-

рактеристикой разомкнутой системы.

Заметим, что все изложенное относится к системам, которые в ра-

зомкнутом состоянии являются устойчивыми и статическими, т. е. в поли-

номе знаменателя передаточной функции разомкнутой системы нет со-

множителя

p .

Рис. 4.13. Годограф вектора

ω)(

Для таких систем, т. е. статических систем автоматического регулиро-

вания, основная формулировка критерия Найквиста следующая: замкнутая

система автоматического регулирования устойчива, если амплитудно-

фазовая частотная характеристика разомкнутой системы не охватывает

точку на вещественной оси, удаленную от начала координат на величину

минус единица.

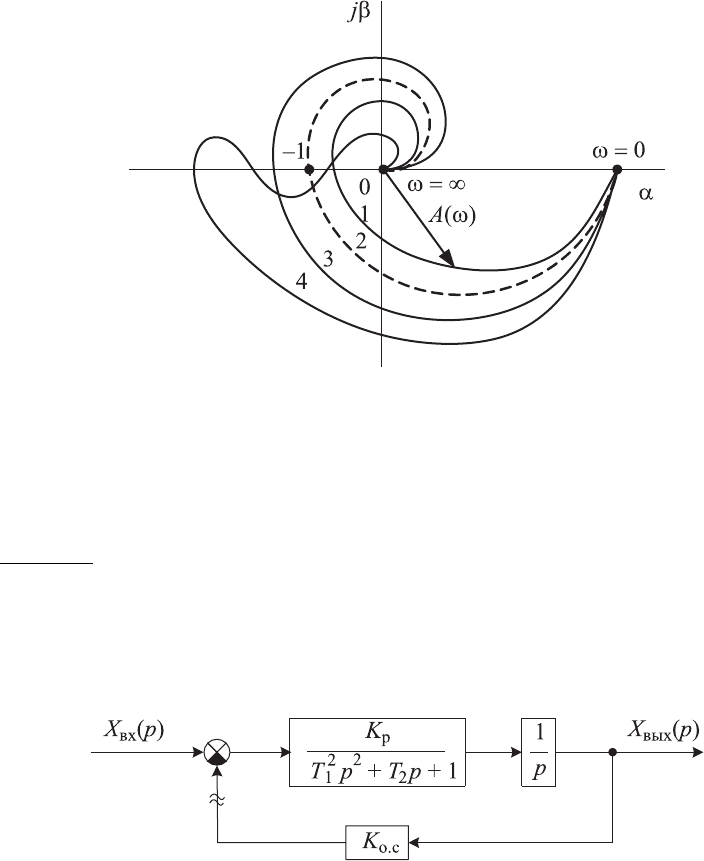
На рис. 4.14 приведены варианты амплитудно-фазовых частотных ха-

рактеристик

для устойчивых и неустойчивых систем.

Рис. 4.14. Амплитудно-фазовые частотные характери-

стикиразомкнутых систем, при которых статическая

замкнутая система: 1, 4 — устойчива; 2 — на границе

устойчивости; 3 — неустойчива

Пример. С помощью критерия Найквиста определить устойчивость

замкнутой системы автоматического регулирования, структурная схема

которой приведена на рис. 4.15, при следующих параметрах:

= 0,5 с, Т

= 1 с, K

= 20, K

о.с

= 0,05.

Рис. 4.15. Структурная схема системы автоматического регулирования

Решение.

Передаточная функция разомкнутой системы

pрТpТ

(p)W

где K = K

о.с

Частотная характеристика

(

)

[

]

222

1)ω(ω

1ωω

ωωω

ω)(

−+

−−

−=

+−−

Тj

TjТ

ТjТ

W .

Вещественную и мнимую частотные характеристики запишем в виде

222

1)ω(ω

) (ω

−+

−=

ТТ

KТ

;

222

1)ω(ω

1)ω(

) (ω

−+

−

I .

Подставляя исходные данные, получим

222

1)(0,25ωω

) (ω

−+

−=R ,

222

1)(0,25ωω

1)(0,25ω

) (ω

−+

−

=I .

Результаты расчета R(ω) и I(ω):

ω 0 0,7 1 1,5 2 2,5 3 ∞

R(ω) –2 –1,56 –1,28 –0,82 –0,5 –0,3 –0,19 0

I(ω) –∞ –1,96 –0,96 –0,24 0 0,07 0,08 0

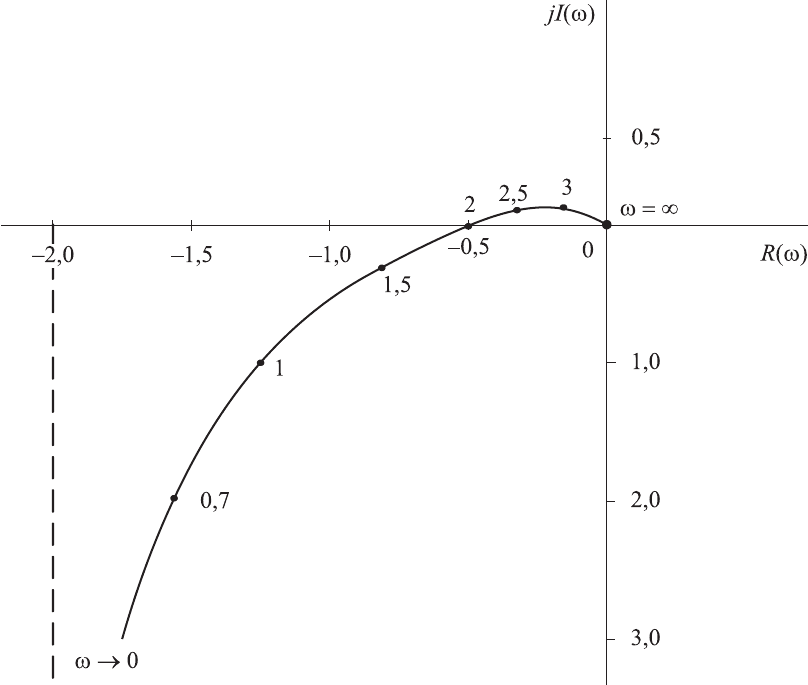
Согласно результатам расчета на рис. 4.16 построена амплитудно-

частотная характеристика разомкнутой системы. Из этого рисунка сле-

дует, что замкнутая система устойчива, так как амплитудно-фазовая час-

тотная характеристика разомкнутой системы не охватывает точку с ко-

ординатами (–1, 0).

Рис. 4.16. Амплитудно-фазовая частотная характеристика

разомкнутой системы

У астатических систем ввиду того, что знаменатель их передаточной

функции содержит сомножитель

p , амплитудно-фазовые частотные харак-

теристики при значениях частот, стремящихся к нулю, уходят в бесконеч-

ность, асимптотически приближаясь к осям координат. При ν = 1 амплитуд-

но-фазовая частотная характеристика уходит в бесконечность, приближаясь

к отрицательной мнимой полуоси, при ν = 2 —

к отрицательной действи-

тельной полуоси, при ν = 3 — к положительной мнимой полуоси и так далее.

Чтобы сделать вывод об устойчивости таких систем, начала амплитудно-

фазовых частотных характеристик, которые находятся в бесконечности, их

амплитудно-фазовые частотные характеристики мысленно дополняют в по-

ложительном направлении дугой бесконечного радиуса до положительной

полуоси. Далее, руководствуясь формулировкой критерия

устойчивости, ре-

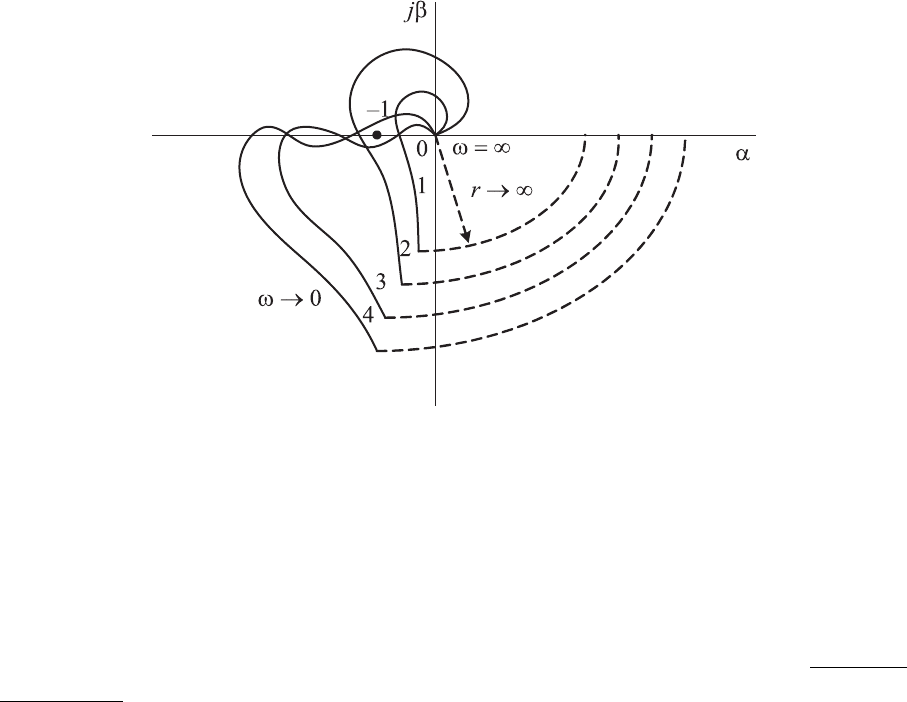
шают вопрос устойчивости системы. На рис. 4.17 приведены амплитудно-

фазовые частотные характеристики астатических устойчивых и неустойчи-

вых систем автоматического регулирования с астатизмом первого порядка.

Рис. 4.17. Амплитудно-фазовые частотные характери-

стики разомкнутых систем, при которых астатическая

замкнутая система: 1, 3 — устойчива;

2, 4 — неустойчива

Для суждения об устойчивости систем, имеющих амплитудно-

фазовые характеристики сложной конфигурации и пересекающих действи-

тельную ось координат левее точки (–1, j0), можно использовать правило

переходов. Согласно этому правилу система устойчива, если при возраста-

нии частоты разность между числом положительных (сверху вниз) и чис-

лом отрицательных (снизу вверх) переходов амплитудно-фазовой частот-

ной характеристики через отрицательную вещественную полуось левее

точки (–1, j0) равна нулю.

Частота, при которой модуль вектора (р)W

принимает значение еди-

ница, называется частотой среза и обозначается

сp

. Графически это озна-

чает, что значение частоты среза соответствует значению частоты, при ко-

торой годограф )(jW ω

пересекает окружность с центром в начале коорди-

нат и с радиусом, равным единице.

4.6. ЛОГАРИФМИЧЕСКИЙ КРИТЕРИЙ

Логарифмический критерий по сути своей является интерпретацией

критерия Найквиста в логарифмической форме. Соответствующим точкам

и значениям амплитудно-фазовой частотной характеристики, очевидно,

будут соответствовать вполне определенные точки и значения логарифми-

ческих амплитудной и фазовой частотных характеристик, т. е. характери-

стики взаимосвязаны. Например, при частоте среза

сp

ω модуль вектора

)(jW ω

равен единице, что соответствует переходу L

(jω) через ось абсцисс

при этой частоте; пересечение годографом )(jW ω

отрицательной вещест-

венной полуоси соответствует пересечению логарифмической фазовой

частотной характеристикой прямой — π. Наиболее наглядно эту связь

можно проследить по различным графикам амплитудно-фазовых частот-

ных характеристик и логарифмических характеристик.

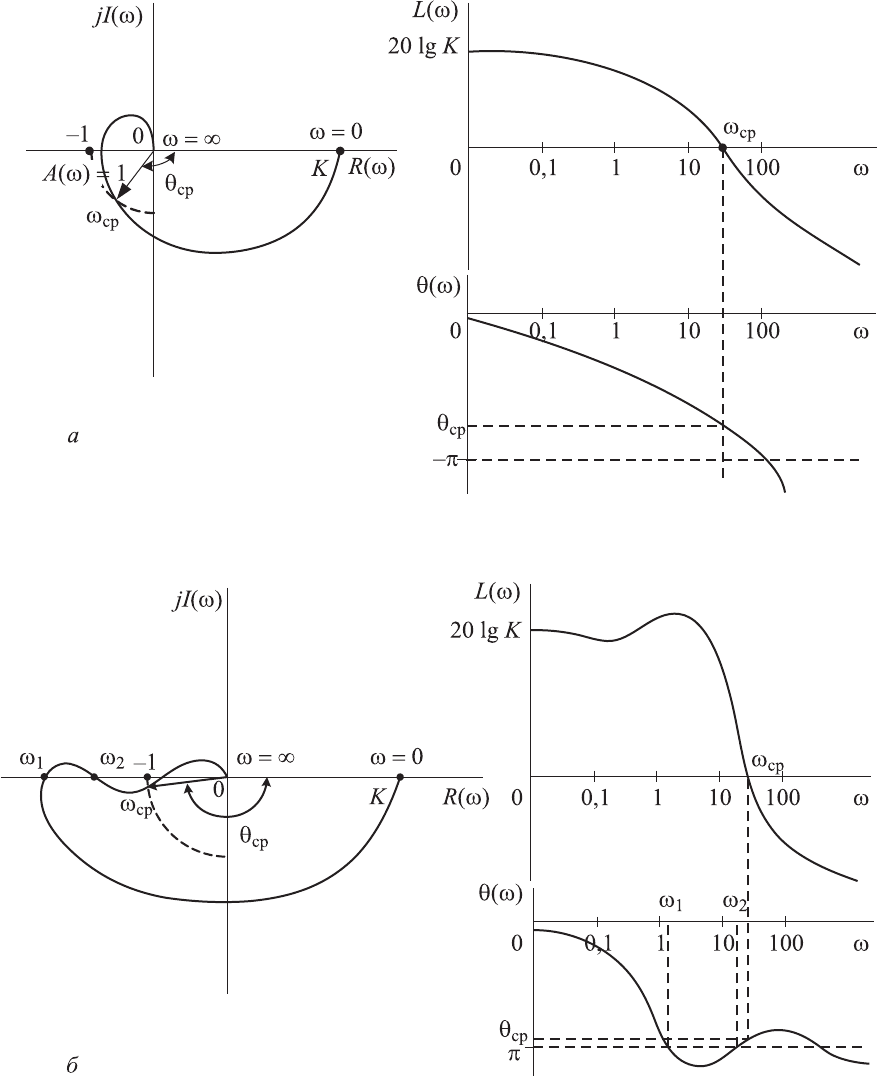
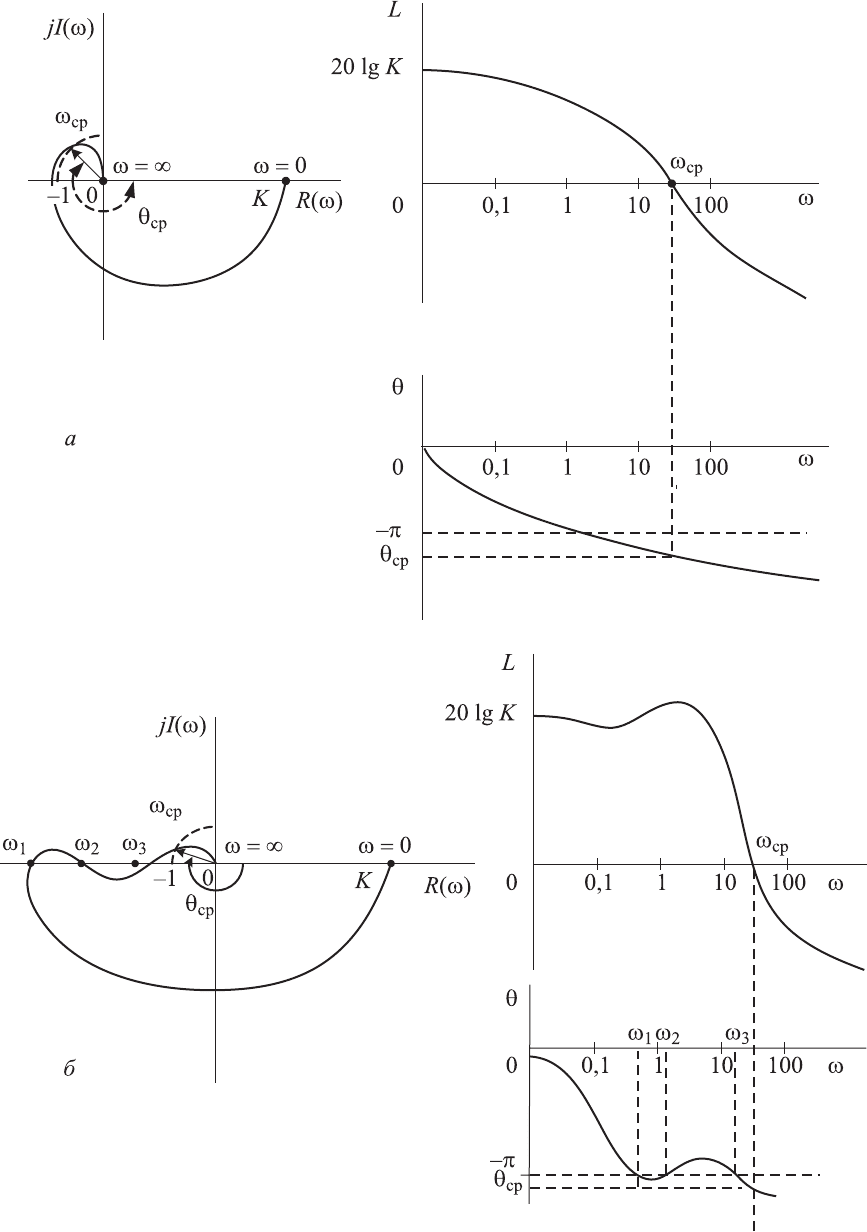
На рис 4.18 приведены амплитудно-фазовые и логарифмические частот-

ные характеристики для устойчивых астатических систем, а на рис. 4.19 —

для неустойчивых астатических систем.

На основании сравнительного анализа этих графиков логарифмиче-

ский критерий можно сформулировать следующим образом: замкнутая

система автоматического регулирования устойчива, если логарифмическая

фазовая частотная характеристика разомкнутой системы не пересекает

прямую –π при значениях частот, меньших значения частоты ω

ср

, а при

амплитудно-фазовой частотной характеристике со сложной конфигураци-

ей число пересечений логарифмической частотной фазовой характеристи-

ки и прямой –π должно быть четным при частотах, меньших частоты среза.

Логарифмический критерий устойчивости, позволяющий судить об

устойчивости замкнутой системы по ее логарифмическим частотным ха-

рактеристикам разомкнутой системы, наиболее удобен в силу относитель-

ной простоты построения логарифмических частотных характеристик ра-

зомкнутой системы.

Пример

. Определить устойчивость астатической системы регулирова-

ния, структурная схема которой представлена на рис. 4.20, на основе лога-

рифмического критерия при следующих значениях параметров:

= 10, K

= 5, K

о.с

= 0,2, Т

= 0,5 с, Т

= 0,33 с.

Решение.

Передаточный коэффициент разомкнутой системы

K = K

о.с

= 2,0510

⋅

= 10.

Находим

20lg1020lg20

дБ

Рис. 4.18. Амплитудно-фазовые и логарифмические частотные характери-

стики статических устойчивых систем автоматического регулирования

Рис. 4.19. Амплитудно-фазовые и логарифмические частотные характери-

стики статических неустойчивых систем автоматического регулирования

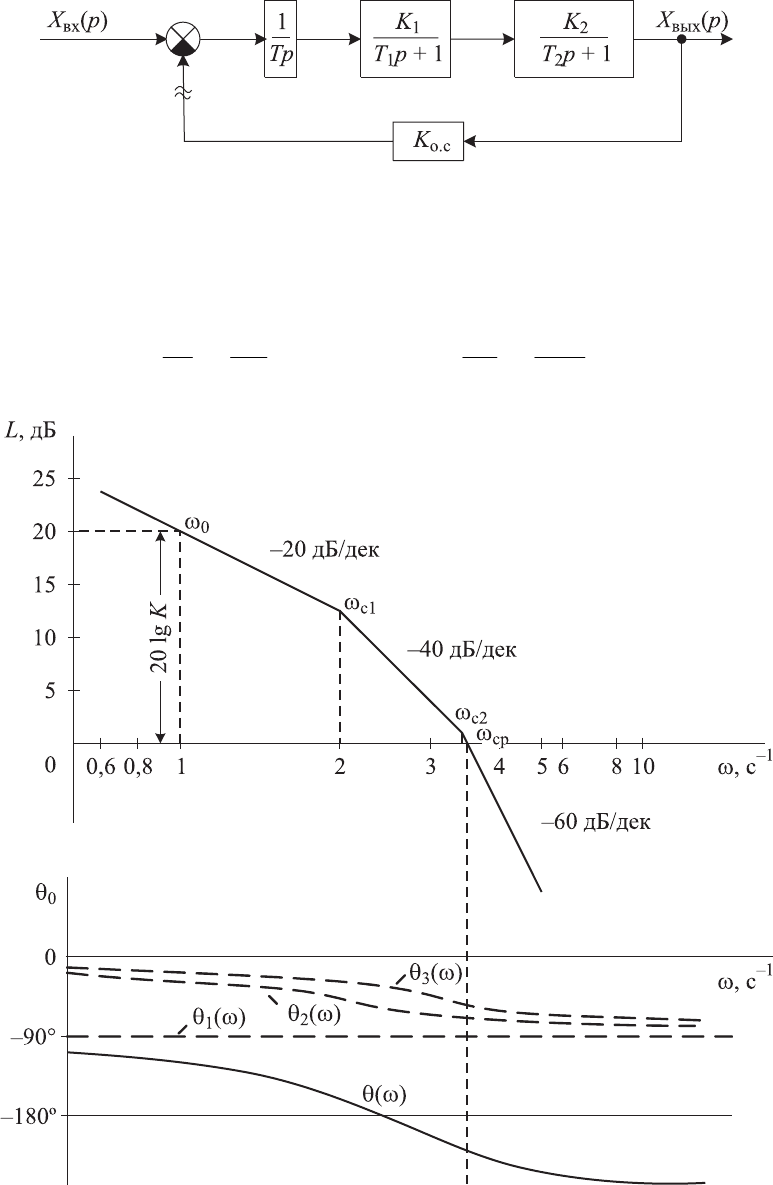
Рис. 4.20. Структурная схема системы автоматического регулирования

и частоты сопряжения логарифмической амплитудной частотной характе-

ристики

с1

с 2

0,5

−

===

с2

с 3

0,33

−

===

Рис. 4.21. Расчетные логарифмические амплитудная частотная

и фазовая частотная характеристики

Согласно полученным значениям на рис. 4.21 построена логарифми-

ческая амплитудная частотная характеристика.