Динкель А.Д. Теория автоматического управления
Подождите немного. Документ загружается.


73
=
++++++
=
р
р
KрТТрТТТpТТ
K
(p)W
1)()(
31
2
31
2
2
32
21
з
1
111
1
31
2
31
2
2
3
2
21
+
+
+
+
+
+
+
+
+
=
р
K
ТТ
р
K
ТТТ
p
K
ТТ
K
K
ррр
р
р
.
Запишем характеристическое уравнение системы:
01
111
31
2
31
2
2
3
2
21
=+
+
+
+
+
+
+
+
р
K
ТТ
р
K
ТТТ
р
K
ТТ
ррр
.
Согласно (4.16) и исходным данным определим значения коэффици-
ентов характеристического уравнения:
K
р
= K
1
K
2
K
о.с
= 19 ⋅ 10 ⋅ 0,1 = 19;
0,00025;
20
0,10,5
1
2
2
21
0
=
⋅
=
+
=
р
K
ТТ
c
0,008
20
0,30,50,1
1
2
31
2
2
1
=
⋅+
=
+
+
=
р
K
ТТТ
c ;
0,04
20
0,30,5
31
=
+
=
+
+
=
р
K1
ТТ
2
c
;
1
3
=
c .
Тогда из определителя
31
20
31
0
0
0
сс
сс
сс
и значений коэффициентов имеем
с
0
> 0;
74
∆
1
= с
1
> 0;
∆
2
= с
1
с
2
–с
0
с
3
= 0,008 ⋅ 0,04–0,00025 ⋅ 1 = 0,00007 > 0;
∆
3
= ∆
2
с
3
= 0,00007 ⋅ 1 = 0,00007 > 0.
Следовательно, система устойчива.
4.4. КРИТЕРИЙ МИХАЙЛОВА
Михайлов, используя известный в теории функций комплексного пе-
ременного принцип аргумента, в 1938 г. сформулировал критерий устой-
чивости систем автоматического регулирования, который по существу яв-
ляется геометрической интерпретацией этого принципа.
Рассмотрим суть принципа аргумента и дадим обоснование рассмат-
риваемого критерия устойчивости.
Пусть дано алгебраическое уравнение с постоянными действительны-
ми коэффициентами:
0λλλ) Д(λ
1
1
10
=++++=
−
−
nn
nn
аа...аа
. (4.19)
Найдя корни этого уравнения и обозначив их через
,,... λλ,λ
21 n
а также используя известную формулу разложения многочлена на множи-
тели, уравнение (4.19) можно представить в следующем виде:
0)λ)(λλ)...(λλ)(λλ(λ) Д(λ
121
=
−
−
−
−=
− nnn
а . (4.20)
Положим
ω
λ
j
=
, тогда
0)λω)(λω)...(λω)(λω() ωД(
121
=−
−
−
−
=
− nnn
jjjjаj . (4.21)
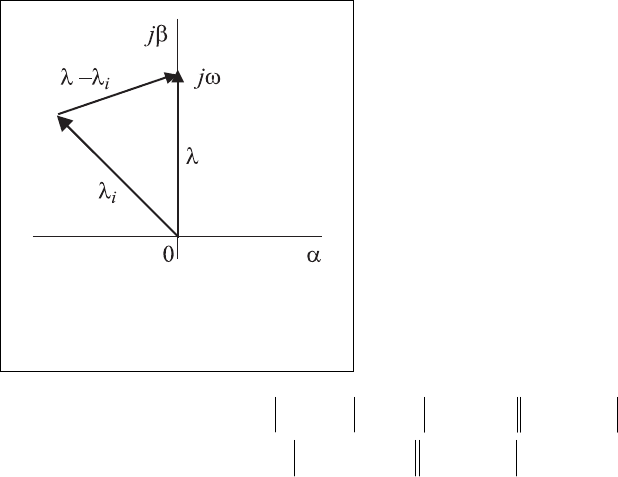
На комплексной плоскости каждому корню
λ
i
соответствует вполне
определенная точка, которая в полярных координатах является концом век-
тора, проведенного из начала координат к этой точке, как это показано на
рис. 4.5. Длина этого вектора равна модулю
λ
i
, а угол его поворота относи-
тельно вещественной оси — аргументу
λ
i
. Независимой переменной jω в
полярных координатах будет соответствовать вектор, совпадающий с мни-
мой осью комплексной плоскости. Тогда вектор с началом в точке
λ
i
и
75
концом в точке j
ω (см. рис. 4.5) будет пред-
ставлять собой разность двух векторов, т. е.
вектор комплексного числа (j
ω–λ). Тогда,
исходя из (4.20), вектор Д(j
ω) является про-
изведением элементарных n векторов, кон-
цы которых все сходятся на мнимой оси в
точке j
ω, как это показано на рис 4.6, и дей-
ствительного числа а
n
: Модуль вектора
Д(j
ω) равен произведению модулей элемен-
тарных векторов и числа а
n
:
0,λωλω
λωλω) ωД(
1
21
=−−
−−=
− nn
n
jj...
...jjаj
(4.22)
а аргумент, или фаза, вектора Д(j
ω) равен сумме аргументов )λω(
i
j − :
0.)λωаrg()λω( аrg ...
)..
.
λω( аrg)λωаrg(ω)Д( аrg
1
21
=−+−
−+−=
− n
jj
jjj
n
(4.23)
При изменении частоты в пределах –∞ ≤ ω ≤ +∞ каждый элементар-
ный вектор )λω(
i
j − , скользящий своим концом по мнимой оси, повер-
нется на пол-оборота, т. е. на угол, равный
π. При этом поворот будет про-
исходить против часовой стрелки (в положительном направлении), если
корень
λ
1
расположен в левой полуплоскости, и по часовой стрелке (в от-
рицательном направлении), если корень
λ
i
расположен в правой полуплос-
кости комплексной плоскости, как это показано на рис. 4.7.
Допустим, что исходное уравнение Д(
λ) = 0 имеет m корней, располо-
женных в правой полуплоскости и, следовательно, n–m корней, располо-
женных в левой полуплоскости. Тогда при изменении частоты от –∞ до +∞
изменение аргумента, или угла поворота, вектора Д(j
ω)
(
)
(
)
ω
∆ arg Д( ω ) ππ 2 πjnmmnm
−∞≤ ≤+∞
=− − =− . (4.24)
Исходя из этого, принцип аргумента формулируется следующим об-
разом. Изменение аргумента вектора Д(j
ω) при изменении частоты от –∞
до +∞ равно разности между числом корней уравнения Д(j
ω) = 0, располо-
женных в левой полуплоскости, и числом корней, расположенных в правой
полуплоскости, умноженной на
π.
Рис. 4.5. Графическое
представление разно-
сти векторов
76
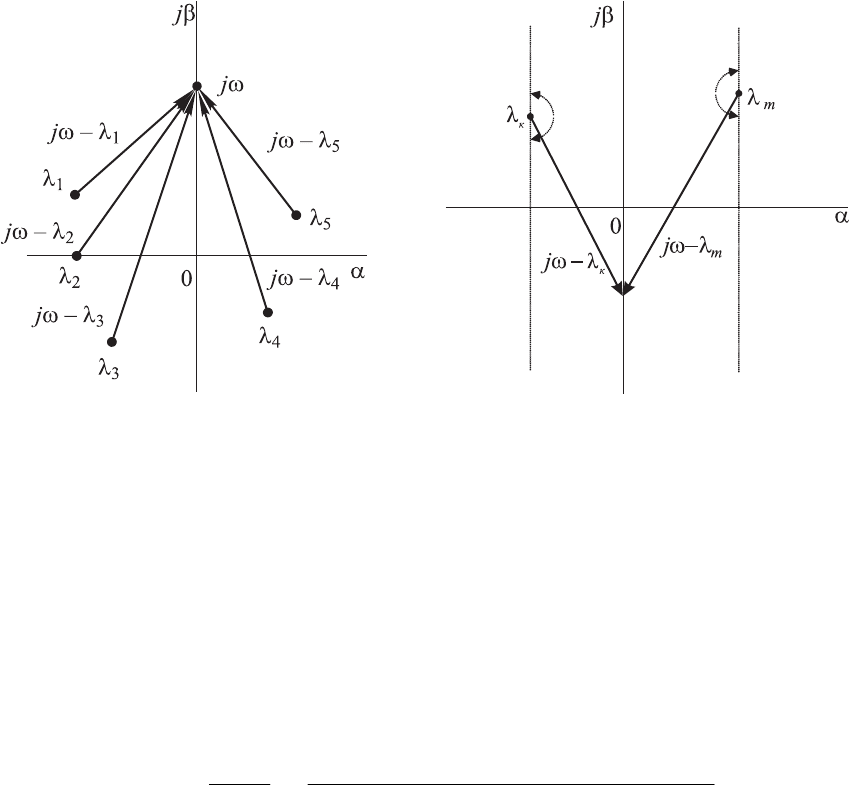
Рис. 4.6. Графическое пред-
ставление векторов сомножи-
телей вида (j
ω–λ
i
)
Рис. 4.7. Расположение векто-
ров j
ω–λ
i
и описываемые ими
углы
Как указывалось выше, критерий устойчивости Михайлова является
геометрической интерпретацией принципа аргумента.
Допустим, что система автоматического регулирования имеет сле-
дующую передаточную функцию:
nn
nn
mm
mm
аpа...pаpa
bpb...pbpb
pQ
pP
pW
++++
++++
==
−
−
−
−
1
1
10
1
1
00
)(
)(
)( . (4.25)
Исходя из этой передаточной функции, характеристическое уравнение
системы записывается в следующем виде:
0)(
1
1
10
=++++=
−
−
nn
nn
аpа...pаpаpQ . (4.26)
Для того чтобы система была устойчива, необходимо, как это следует
из условия устойчивости, чтобы все корни характеристического уравнения
(4.19) лежали в левой полуплоскости комплексной плоскости, т. е. чтобы
m = 0. В этом случае согласно (4.24) изменение аргумента
πω аrg ∆
ω
n)Q(j =
+∞≤≤∞−
. (4.27)
Уравнение характеристической кривой

77
ω)( jQ = 0 (4.28)
получается из (4.26) путем подстановки p = jω:
0ωω)(ω)(ω)(
1
1
10
=++++=
−
−
nn
nn
аjа...jаj аjQ
. (4.29)
Геометрическое место точек конца вектора ω)( jQ на комплексной
плоскости при изменении частоты в пределах –∞ ≤ ω ≤ +∞ называется го-
дографом вектора ω)( jQ или годографом Михайлова.
Разделяя ω)( jQ на вещественную и мнимую составляющие:
)(ω)(ω) ω( j
I
R
jQ
+
=
, (4.30)
получили
...ωω ) (ω
4
4
2
2
−+−=
−− nnn
аааR
; (4.31)
...ωωω) (ω
5
5
3
31
−+−=
−−− nnn
аааI
(4.32)
Из (4.31) и (4.32) следует, что
)(ωω)(
R
R
=
−
,
)ω()ω(
I
I
−
=
−
,
т. е. R(ω) — четная функция, I(ω) — нечетная функция.
Следовательно,
)(ω)(ω) ω( j
I
R
Q
+
=j при ω > 0; (4.33)
)(ω)(ω) ω( j
I
R
Q
−
=− j при ω < 0. (4.34)
Это свидетельствует о том, что характеристическая кривая симмет-
рична относительно вещественной оси. Поэтому при построении характе-
ристической кривой на комплексной плоскости, можно ограничиться диа-
пазоном изменения частоты ω от нуля до плюс бесконечности. В этом слу-
чае угол поворота вектора Q(jω) изменяется в два раза,
а следовательно,
изменение аргумента для устойчивой системы равно:
2
π
) ωQ( аrg ∆
ω
nj =
+∞≤≤∞−
. (4.35)

78
Из (4.35) следует формулировка критерия устойчивости Михайлова.
Система автоматического регулирования устойчива, если при изменении
частоты от 0 до +∞ вектор Q(jω) повернется на угол
2
π
n , или, иначе, если
годограф вектора Q(jω) с ростом частоты от 0 до +∞, начинаясь на дейст-
вительной оси, обходит последовательно в положительном направлении
(против часовой стрелки) n квадрантов.
На рис. 4.8, а показаны годографы Q(jω) устойчивых систем для раз-
ных значений n. Все они последовательно проходят через
соответствую-
щее число квадрантов в положительном направлении.
На рис. 4.8, б показаны годографы неустойчивых систем. Все они не
удовлетворяют условию обхода n квадрантов в положительном направле-
нии.
Рис. 4.8. Годографы вектора Q(j
ω) для устойчивых систем (а)
и неустойчивых систем (б)
Если годограф Q(jω) проходит через начало координат, то система на-
ходится на границе устойчивости.
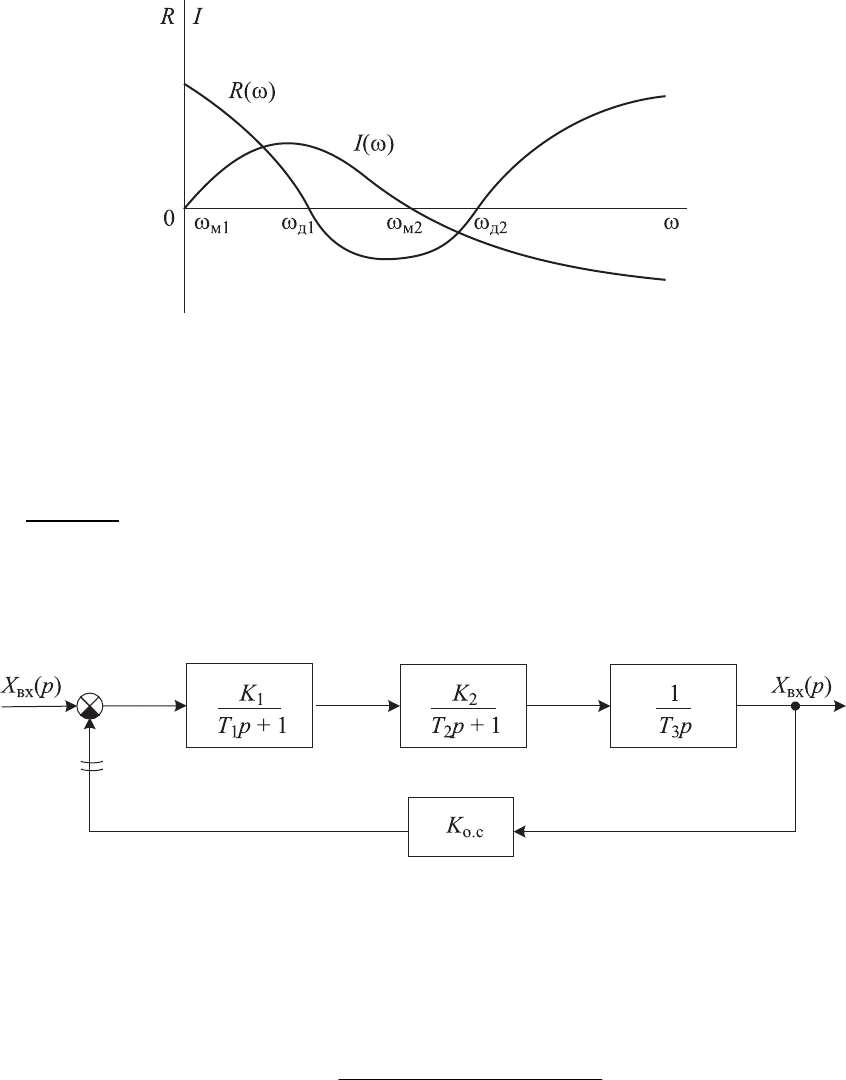
В практических расчетах удобно применять следствие критерия Ми-
хайлова: система автоматического регулирования устойчива, если дейст-
вительная R(ω) и мнимая I(ω) части характеристической кривой Q(jω) об-
ращаются в нуль поочередно (рис. 4.9).
79
Рис. 4.9. Графики изменения вещественной
и мнимой составляющих
) ω( jQ
Критерий устойчивости Михайлова применим как к разомкнутым, так
и замкнутым системам автоматического регулирования.
Пример
. С помощью критерия Михайлова определить устойчивость
замкнутой системы автоматического регулирования, структурная схема
которой приведена на рис. 4.10, при следующих параметрах: Т
1
= 0,1 с, Т
2
= 3 с, Т
3
= 2 с, K
1
= 20, K
2
= 10, K
о.с
= 0,05.
Рис. 4.10. Структурная схема системы автоматического регулирования
Решение.
Передаточная функция разомкнутой системы
pТрТpТ
KKK
(p)W
321
о.с
21
p
1)1)(( ++
= .
Передаточная функция замкнутой системы
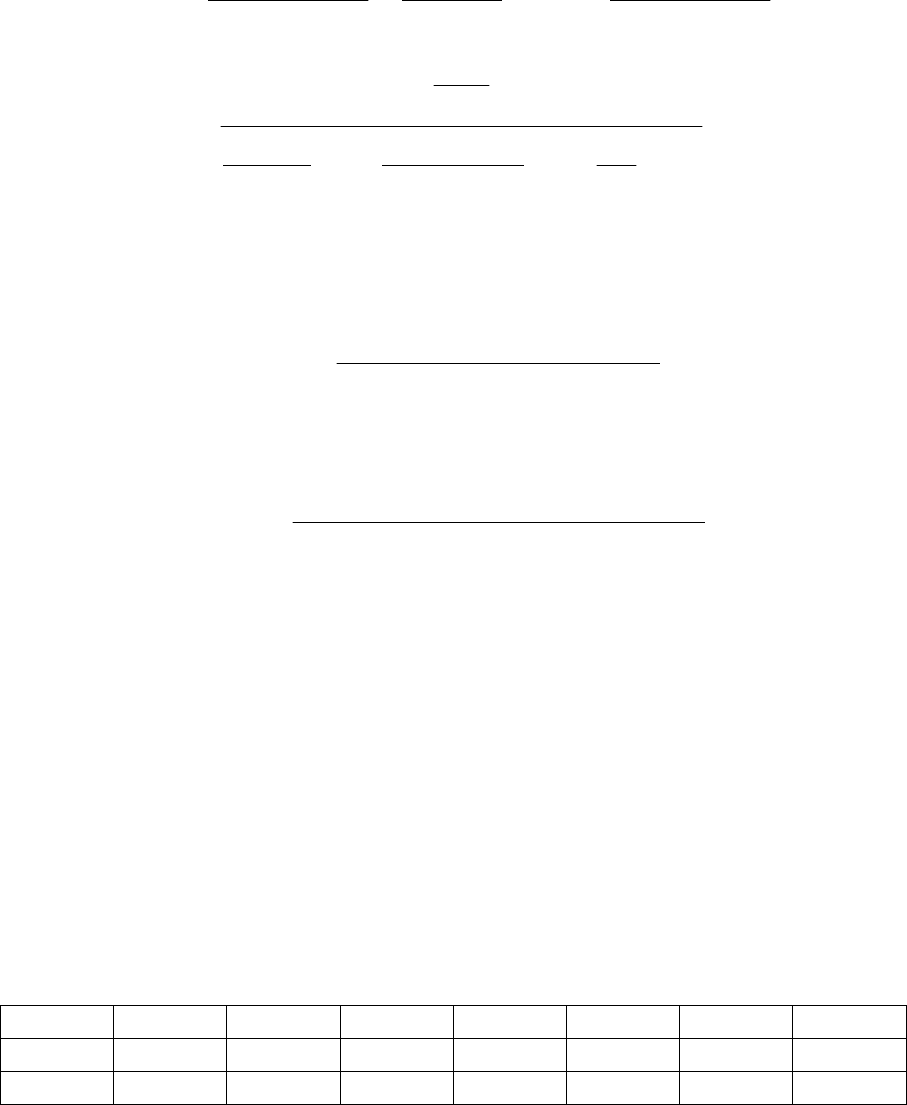
80
=
+
=
(p)WK
(p)W
(p)W
ро.с
р
з
1
(p)Х
(p)X
вх
вых
=
+
=
(p)WK
(p)W
(p)W
ро.с
р
з
1
1
)(
1
р
3
2
р
321
3
р
321
о.с
++
+
+
=
р
K
Т
р
K
ТТТ
p
K
ТТТ
K
,
где K
р
= K
1
K
2
K
о.с
— передаточный коэффициент разомкнутой системы.
Подставляя исходные данные, получим
10,20,620,06
20
23
з
+++
=
ррр
(p)W .
Частотная характеристика
10,2ω0,62ω0,06ω
20
23
з
+⋅+−⋅−
=
jj
(p)W .
Запишем характеристическое уравнение
10,2ω0,62ω0,06ωω)(
23
++−−= jjjQ = 0.
Вещественная и мнимая части характеристики
2
0,62ω1) (ω −=R
,
)0,06ωω(0,2) (ω
2
−=I
.
Результаты расчета R(ω) и I(ω):
ω 0 0,5 1 1,27 1,79 2 2,5
R(ω) 1 0,85 0,32 0 –1 –1,49 –2,9
I(ω) 0 0,09 0,14 0,13 0,03 –0,08 –0,44
Согласно результатам расчета на рис. 4.11 построен годограф вектора
)ω( jQ . Из этого рисунка следует, что система устойчива, так как годограф
вектора )ω( jQ поочередно проходит через три квадранта комплексной
плоскости в соответствии с порядком характеристического уравнения.

81
Рис. 4.11. Годограф вектора
)( ωjQ
Об устойчивости системы можно судить на основании следствия кри-
терия Михайлова. Для этого определим положительные корни уравнений
2
0,62ω1) (ω −=R = 0,
)ω 0,06ω(0,2) (ω
2
−=I = 0.
Положительные корни:
1,612ω
1
= — для первого уравнения,
1,8ω
0ω
3
2
=
=
— для второго уравнения.
Полученные значения корней свидетельствуют о том, что R(ω) и I(ω)
обращаются в нуль поочередно, а следовательно, система устойчива.

82
4.5. КРИТЕРИЙ НАЙКВИСТА
Этот критерий, основанный на использовании частотных характери-
стик, предложен Найквистом в 1932 г. для исследования устойчивости уси-
лителей с обратной связью. Позднее Михайлов, в 1938 г., по-новому
обосновал этот критерий и показал возможность его применения для ана-
лиза устойчивости систем автоматического регулирования. В основу кри-
терия Найквиста также положен принцип аргумента.
Этот
критерий, в отличие от рассмотренных критериев Рауса, Михай-
лова, Гурвица, позволяет судить об устойчивости замкнутой системы ав-
томатического регулирования по амплитудно-фазовой частотной характе-
ристике этой системы в разомкнутом
состоянии.
Допустим, что передаточная функция системы в разомкнутом состоянии
(p)Q
(p)P
(p)W
р
р
р
= . (4.36)
Следовательно, передаточная функция замкнутой системы с единич-
ной обратной связью
(p)Q(p)P
(p)P
(p)W
(p)W
(р)W
рр
р
р
р
З
1 +
=
+
=
. (4.37)
Соответственно, комплексные частотные характеристики разомкнутой
и замкнутой систем можно записать в следующем виде:
) ω(
) ω(
р
р
р
j
j
Q
P
) (jωW = ; (4.38)
) ω() ω(
) ω(
) ω(
pp
p
З
jj
j
j
QP
P
W
+
= . (4.39)
Образуем новую функцию:
=
+
= ) ω(1) ω(
p
jjWF
) ω(
ω)(ω)(
p
pp
j
jj
Q
PQ
+
. (4.40)
