Динкель А.Д. Теория автоматического управления

Подождите немного. Документ загружается.

203

В любой точке фазовой плоскости, где переменная у и функция f

(x, y)

не равны нулю, фазовая траектория имеет только одно определенное на-

правление, соответствующее значению производной dy / dx в данной точке.

Из этого следует, что фазовые траектории в таких точках не пересекаются.

Согласно выражению (9.3) при у = 0 производная dy / dx = ∞, т. е. фа-

зовые траектории пересекают ось x под прямым

углом, а переменная х дос-

тигает своего максимума. Если при у = 0 одновременно f

(x, y) = 0, то фа-

зовая траектория в таких особых точках плоскости не имеет определенного

направления, а производные от х и у согласно уравнениям (9.1) равны ну-

лю. Последнее означает, что изображающая точка неподвижна, а система

регулирования находится в состоянии равновесия.

Особые точки могут быть обособленными и образовать особые отрез-

ки на

оси х. Такие отрезки называются отрезками покоя. Если в импульс-

ную характеристику входит нелинейный элемент с зоной нечувствитель-

ности, то длина отрезка покоя равна ширине зоны нечувствительности.

Самые важные для анализа нелинейных систем свойства фазовых тра-

екторий заключаются в следующем:

1. Затухающему (устойчивому) переходному процессу (см. рис. 9.5, а)

соответствует фазовая траектория,

сходящаяся к началу координат или от-

резку покоя;

2. Неустойчивому процессу (см. рис. 9.5, б) соответствует фазовая

траектория, удаляющаяся от начала координат;

3. Периодическому процессу (см. рис. 9.5, в) соответствует замкнутая

фазовая траектория, называемая предельным циклом.

Предельный цикл может быть устойчивым или неустойчивым. Если

все соседние фазовые траектории стягиваются к предельному циклу, то он

является устойчивым и соответствует автоколебаниям. Если же соседние

траектории отходят от цикла, то он является неустойчивым.

Фазовый портрет нелинейной системы, нелинейный элемент которой

имеет кусочно-линейную или разрывную характеристику, состоит из не-

скольких областей с различными фазовыми траекториями. Линии, отде-

ляющие на плоскости одну область от другой, называются линиями пере-

ключения.

В точках пересечения фазовыми траекториями линий переключения

происходит излом траекторий. Это обусловлено сменой правой части урав-

нения (9.3).

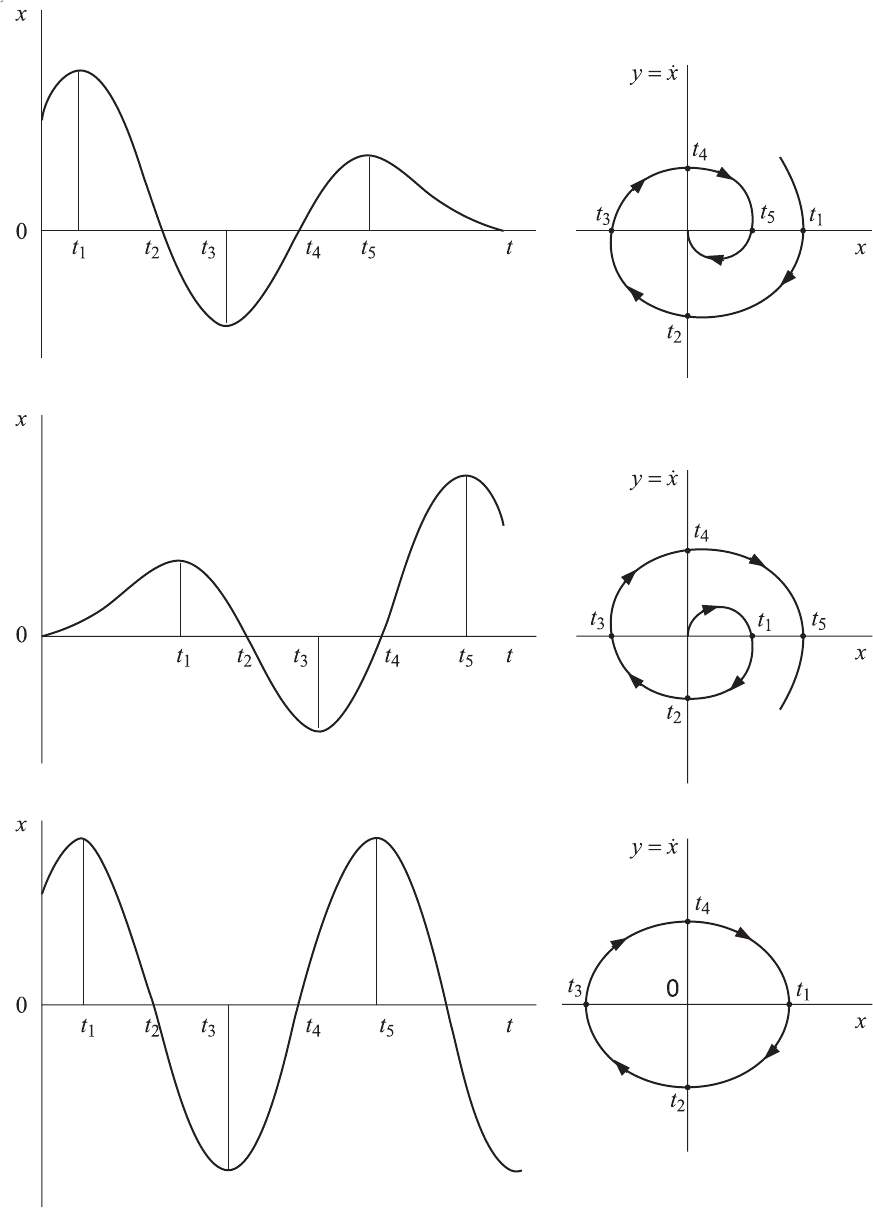
204

Рис. 9.5. Переходные процессы и фазовые траектории нелинейной системы:

а — устойчивой; б — неустойчивой; в — на границе устойчивости

205

Пример 9.1. Построим фазовый портрет нелинейной системы автома-

тического регулирования, структурная схема которой приведена на рис.

9.6, а. Объект регулирования представлен последовательно соединенными

интегрирующим звеном и инерционным звеном первого порядка.

Будем рассматривать процессы в системе при х

= 0. Тогда согласно

структурной схеме уравнение замкнутой системы запишется в следую-

щем виде:

Kf(x)

Т −=+

. (9.5)

В соответствии с характеристикой нелинейного элемента, приведен-

ной на рис. 9.5, б, нелинейная функция

⎪

⎩

⎪

⎨

⎧

−<−

.при

,при0

,при

bхс

b|х|

bх

f(x)

(9.6)

Рис. 9.6. Структурная схема нелинейной системы (

а)

и характеристика нелинейного элемента (

б)

Уравнение (9.5) эквивалентно системе двух уравнений первого поряд-

ка, записанной в форме Коши:

⎪

⎭

⎪

⎬

⎫

−=+

Kf(x)z

. (9.7)

Разделив второе уравнение на первое, получим нелинейное уравнение

фазовых траекторий:

206

⎥

⎦

⎤

⎢

⎣

⎡

−−= f(x)

. (9.8)

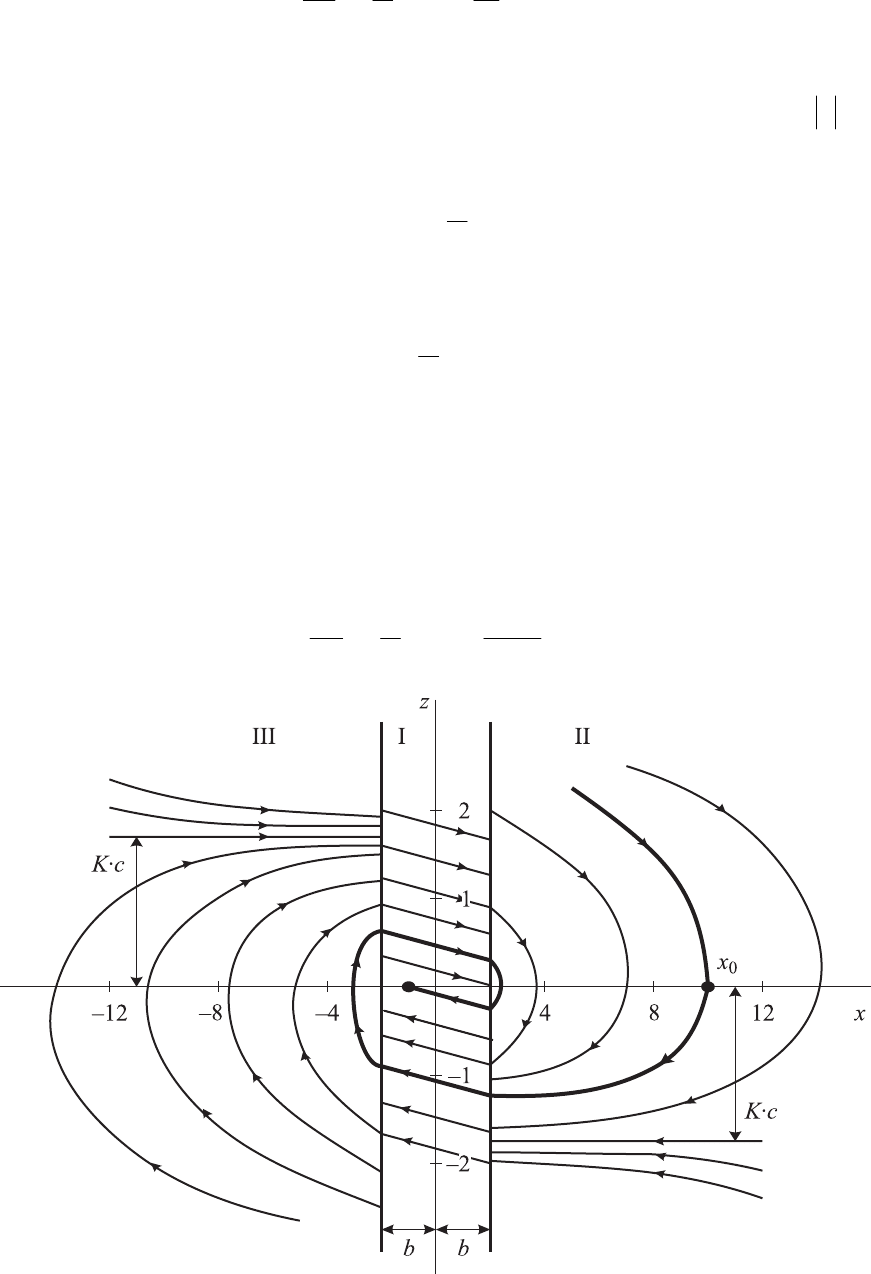
В соответствии с видом функции (9.6) фазовую плоскость делим на

три области (рис. 9.7). В области I, соответствующей значениям

bх

уравнение (9.8) примет вид

z d

d −= . (9.9)

Решение этого уравнения:

z +−= , (9.10)

где С

— постоянная интегрирования.

Таким образом, в средней области I фазовые траектории представляют

собой прямые линии с отрицательным наклоном, равным 1/T.

В областях II и III, где соответственно х > b и x < b, а f(x) = +с

и f(x) = — с, уравнение (9.8) примет такой вид

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−=

сK

Тx

. (9.11)

Рис. 9.7. Фазовый портрет системы

207

Разделяя переменные x и z, получим

сKz

x dd

⋅±

−= . (9.12)

После интегрирования (9.12) находим уравнение фазовых траекторий:

(2,3)

ln СсKzсKТ(zх +⋅±⋅⋅±−= , (9.13)

где верхние знаки относятся к области II, а нижние — к области III.

На рис. 9.7 приведены фазовые траектории, построенные при различ-

ных значениях постоянных интегрирования C

(1,2,3)

и следующих парамет-

рах: Т = 10 с, K = 0,04 с

–1

, с = 50, b = 5.

Жирной линией выделена фазовая траектория, соответствующая на-

чальному отклонению х

= 10.

По фазовому портрету видно, что после любых начальных отклонений

х и z в системе происходит затухающий колебательный процесс, который

продолжается до тех пор, пока отклонения х не станут меньше зоны нечув-

ствительности b = 2.

9.4. МЕТОД ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ

Метод гармонической линеаризации является приближенным частот-

ным методом исследования режима автоколебаний в нелинейных системах.

На основе этого метода можно определить условия возникновения и пара-

метры автоколебаний в системе как второго, так и более высокого порядка.

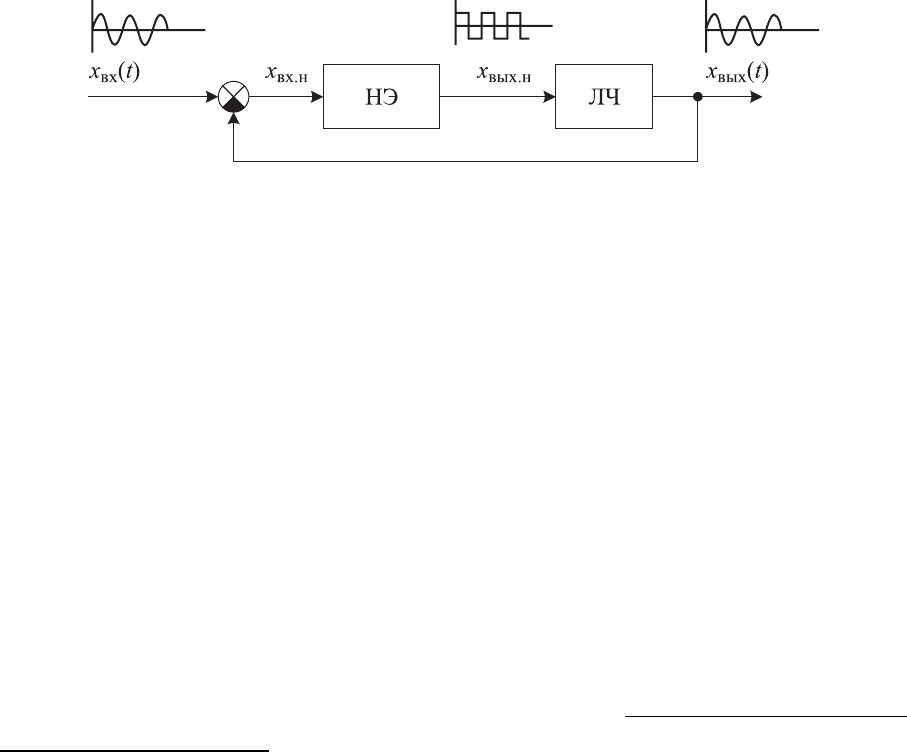
Нелинейная система с одним нелинейным элементом, как показано

выше, может быть приведена к схеме, в которой

нелинейный элемент

включен последовательно с линейной частью, объединяющей все линей-

ные элементы.

Предполагается, что в такой нелинейной замкнутой системе (рис. 9.8),

на вход которой поступает гармонический сигнал, входной сигнал нели-

нейного элемента будет изменяться по гармоническому закону.

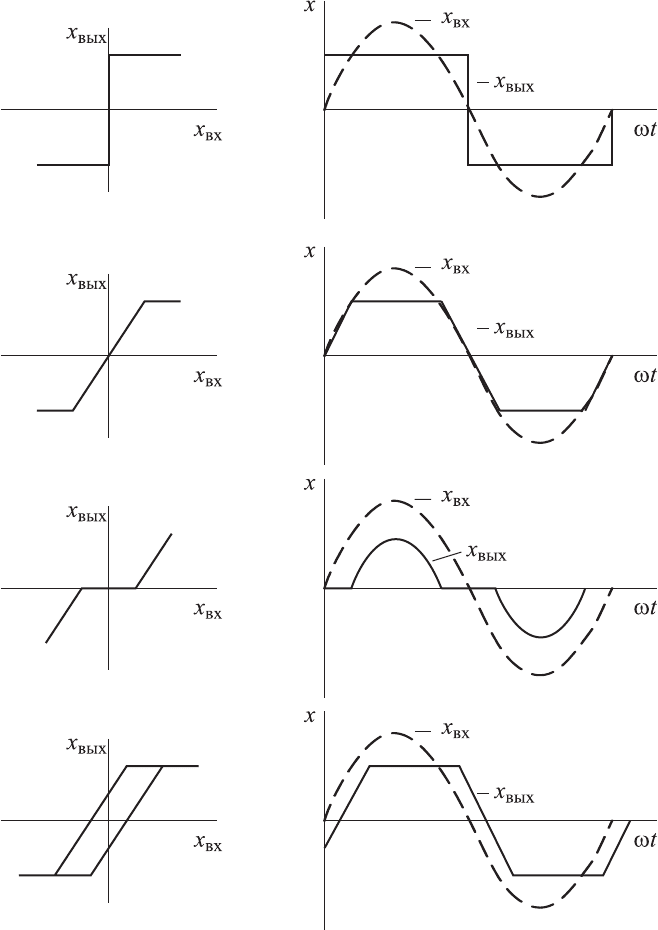
Сигнал на выходе нелинейного элемента, как это видно из рис. 9.9,

будет периодическим и совпадающим

по частоте с частотой входного гар-

монического сигнала, но содержащим высшие гармоники.

208

Рис. 9.8. Структурное представление нелинейной системы

Следовательно, вышепринятое предположение допустимо, если ли-

нейная часть системы будет являться фильтром низких частот. Тогда все

высшие гармоники, поступающие на вход линейной части, будут значи-

тельно ослабляться, и выходной сигнал линейной части можно принять

гармоническим.

Такое допущение в процессах, протекающих в нелинейной системе,

позволяет с достаточной точностью для практических расчетов определять

условия устойчивости системы, судить о возможности возникновения ав-

токолебательных режимов и определять их параметры. На этой базе можно

также давать оценку качества процесса регулирования и решать вопросы

синтеза системы.

Таким образом, анализ нелинейной системы в данном случае произ-

водится исходя из предположения, что движение системы имеет гармони-

ческий характер. Это

позволяет ввести понятие о передаточной функции

нелинейного элемента.

В общем случае, в зависимости от характеристики нелинейного эле-

мента, сигнал на выходе нелинейного элемента является функцией входно-

го сигнала и его производной х

),(

вх.нвх.нвых.н

ххfх

. (9.14)

Если на вход нелинейного элемента в соответствии с принятым пред-

положением поступает гармонический сигнал

tхх

ωsin

н.мвх.н

, (9.15)

где х

н.м

— амплитуда входного сигнала,

и производная гармонического сигнала

tхх

ω cos ω

н.мвх.н

, (9.16)

то выходной сигнал нелинейного элемента является периодической функцией

)ω cos,ωsin

н.м

н.мвых.н

tхtf(х(t)х

. (9.17)

209

Рис. 9.9. Характеристики нелинейных элементов

и графики их входных и выходных сигналов

Разлагая (9.17) в ряд Фурье:

)ωcosω sin (

0вых.н

t K btK aA(t)х

∑

++=

∞

, (9.18)

где а

, b

— коэффициент Фурье,

и учитывая, что для нелинейных элементов с кососимметричными харак-

теристиками A

выражение для первой гармоники выходного сигнала не-

линейного элемента запишем в следующем виде:

210

t ω cosωsin

вых.н

bt a(t)х

. (9.19)

Исходя из (9.15) и (9.16)

,ωsin

н.м

вх.н

= (9.20)

н.м

вх.н

ω cos

= . (9.21)

Тогда (9.19) запишется в следующем виде:

н.м

вх.н

н.м

вх.н

вых.н

ωх

а(t)х

+= . (9.22)

Введя обозначения

н.м

)(

хq = ,

н.м

н.м1

)(

хq =

получим

)()()()()(

вх.нн.м1вх.нн.мвых.н

tххqtххqtх

= . (9.23)

Таким образом, выполнив указанные выше действия, нелинейное

уравнение (9.17) заменили линейным уравнением (9.23). Эта операция на-

зывается гармонической линеаризацией

, а коэффициенты )(

н.м

хq и

)(

н.м1

хq — коэффициентами гармонической линеаризации и могут быть

определены по известной методике определения коэффициентов Фурье.

Выражения для определения этих коэффициентов применительно к наибо-

лее часто встречающимся нелинейностям приведены в табл. 9.2. При этом

амплитуда выражена в безразмерных единицах через базовый параметр b:

н.м

Гармоническая линеаризация принципиально отличается от обычной

линеаризации в силу того, что коэффициенты гармонически линеаризо-

211

ванного элемента непостоянны и зависят от амплитуды

н.м

х входного сиг-

нала. Однако при определенном режиме периодических колебаний, когда

значение частоты ω и амплитуды

н.м

х фиксированы, коэффициенты гар-

монической линеаризации имеют постоянные значения. Благодаря этому

решение некоторых задач анализа нелинейных систем может быть выпол-

нено с использованием методов теории линейных систем автоматического

регулирования.

Тогда, представив (9.23) в операторной форме:

)()()()()(

вх.нн.м1вх.нн.мвых.н

tрххqрХхqрХ

= , (9.24)

можно получить эквивалентную передаточную функцию нелинейного

элемента

)(

ω),,(

н.м1н.м

вых.н

н.мн

рХ

хрW +==

вх.н

, (9.25)

а подстановкой в нее

ωjр =

— эквивалентную амплитудно-фазовую час-

тотную характеристику

).()()(

н.м1н.мн.мн

хjqхqхW

(9.26)

Модуль функции (9.26)

н.м1

н.мн.мн

][][ )()()( хqxqхА += , (9.27)

определяет отношение первой гармоники выходного сигнала к амплитуде

входного сигнала, а аргумент этой функции

)(

arctg)()(arg

н.м

н.м1

н.мн.мн

хq

ххW =ϕ= (9.28)

является фазовым сдвигом между первой гармоникой выходного сигнала и

гармоническим входным сигналом.

Необходимо отметить, что у всех нелинейностей с однозначной ха-

рактеристикой 0)(

н.м1

=хq , т. е. нет сдвига по фазе между выходным и

входным сигналами.

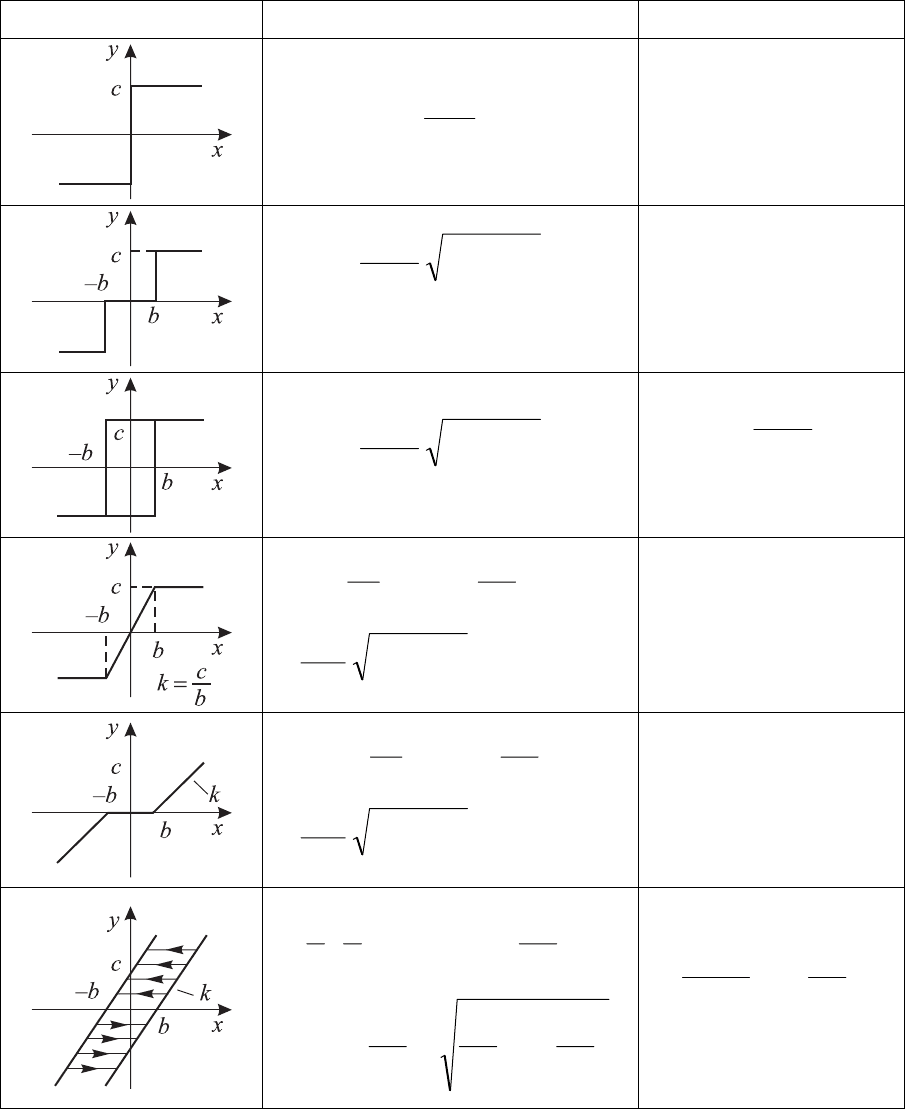
212

Таблица 9.2

Коэффициенты гармонической линеаризации

типовых нелинейностей

= f(х

) q(х

) q

(х

)

bх

−

при

bх

−

bх

−

при

bхbх

>−+

⎟

⎠

⎞

⎜

⎝

⎛

при

sinarc

bхbх

>−+

⎟

⎠

⎞

⎜

⎝

⎛

−

при

sinarc

⎥

⎦

⎤

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

mmm

–1

–12

–1sinarc

bх

⎟

⎠

⎞

⎜

⎝

⎛

при

4–

–