Динкель А.Д. Теория автоматического управления

Подождите немного. Документ загружается.

193

== (q)(q)ХW(q)Х

вх

вых

(q)Х

(q)Q

(q)P

вх

, (8.39)

которое связывает изображения сигналов, представленных в дискретной

форме, на входе и выходе импульсной системы. Следовательно, зная ха-

рактер изменения входного сигнала и дискретную передаточную функцию

замкнутой системы, можно из (8.39), переходя от изображений к оригина-

лам, используя формулу обратного дискретного преобразования Лапласа,

определить характер изменения оригинала выходного сигнала импульсной

системы. Значение

выходного сигнала в дискретные моменты времени

][

вых

nх

∑

nх

],[

)(

(0)

вх

(8.40)

где q

— корни характеристического уравнения

0)(

=qQ

;

m — порядок характеристического уравнения.

Переходную характеристику импульсной системы можно получить

приближенным графоаналитическим методом по импульсной веществен-

ной частотной характеристике, аналогично методу, применяемому в не-

прерывных системах.

194

ГЛАВА 9. НЕЛИНЕЙНЫЕ СИСТЕМЫ

АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

Система автоматического регулирования является нелинейной, если хо-

тя бы один элемент, входящий в структуру этой системы, является нелиней-

ным, т. е. зависимость выходного сигнала от входного (характеристика) этого

элемента в статике или динамике описывается нелинейными уравнениями.

Различают два вида нелинейных элементов: существенно нелинейные

и несущественно нелинейные. Нелинейность является несущественной

если ее замена нелинейным элементом не изменяет принципиальных осо-

бенностей системы и процессы в линеаризованной системе качественно не

отличаются от процессов в реальной системе. Если такая замена приводит

к сильному отличию процесса в линеаризованной системе от процесса

в реальной системе, то нелинейность является существенной

Принципиальными особенностями существенно нелинейных систем

являются: невозможность применения принципа наложения (суперпози-

ции), зависимость показателей качества процесса регулирования и условий

устойчивости от величины и формы внешнего воздействия. В связи с этим,

применительно к существенно нелинейным системам введены понятия «ус-

тойчивость в малом», «устойчивость в большом» и «устойчивость в целом».

Специфическим режимом

для нелинейных систем является режим ав-

токолебаний. Автоколебания

— это устойчивые собственные колебания

системы, возникающие вследствие нелинейных свойств самой системы.

Рассмотрению этого режима уделяется особое внимание.

Нелинейные системы автоматического регулирования описываются не-

линейными уравнениями. Существует ряд точных и приближенных методов

решения задач анализа нелинейных систем, к числу которых относятся:

–

отыскание возможных состояний равновесия системы и оценка их

устойчивости;

–

определение возможности существования автоколебаний и выявле-

ние их устойчивости;

–

установление соотношений между параметрами системы, при ко-

торых возникают автоколебания;

–

определение параметров автоколебаний и их связи с параметрами

системы.

195

9.1. СТРУКТУРНАЯ СХЕМА НЕЛИНЕЙНОЙ СИСТЕМЫ

И ХАРАКТЕРИСТИКИ НЕЛИНЕЙНЫХ ЭЛЕМЕНТОВ

В общем случае нелинейную систему регулирования можно предста-

вить в виде последовательно соединенных нелинейной и линейной частей,

охваченных обратной связью и воздействующих на эту систему управ-

ляющего (входного) и возмущающего сигналов (рис. 9.1).

Прежде чем приступить к анализу нелинейной системы любой слож-

ности, в ней необходимо в явном виде выделить нелинейную и

линейную

части и привести ее к виду, представленному на рис. 9.1.

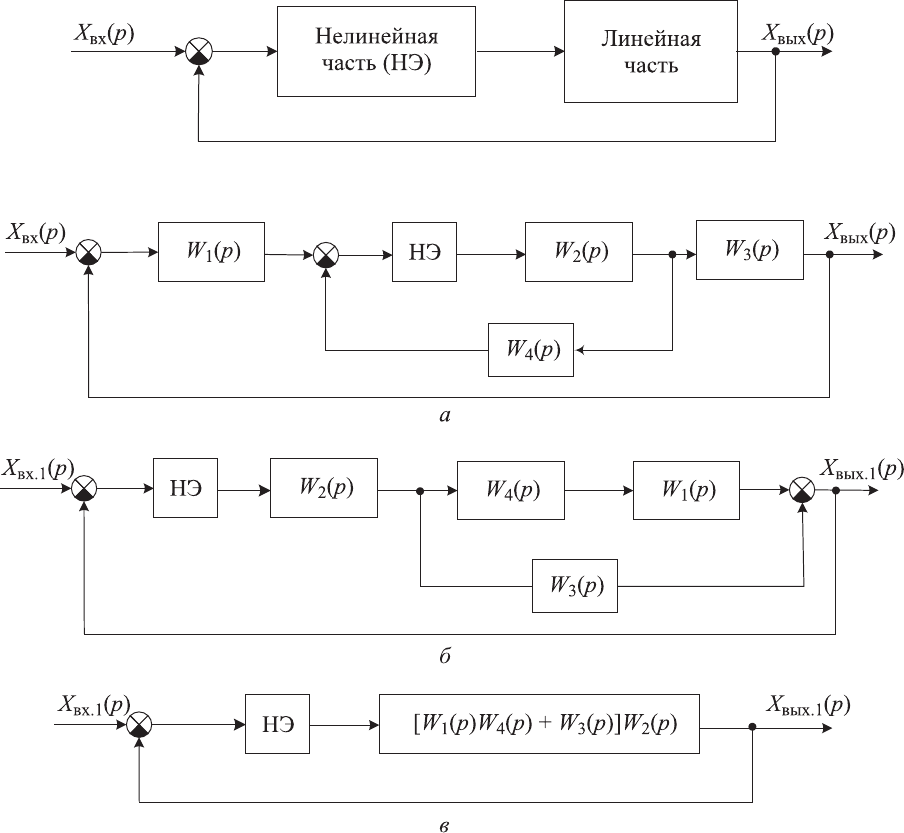
Рис. 9.1. Структурная схема нелинейной системы

Рис. 9.2. Структурные схемы нелинейной системы с НЭ в прямом канале:

а — исходная; б — преобразованная; в — приведенная

196

В практически применяемых нелинейных системах регулирования со-

держится, как правило, один существенно нелинейный элемент, включен-

ный в прямой канал регулирования или в какую-либо цепь обратной связи.

Рассмотрим импульсную систему регулирования, в которой нелиней-

ный элемент находится в прямом канале, как это показано на рис. 9.2, а.

По структурно преобразованной схеме (

см. рис. 9.2, б) получена однокон-

турная приведенная схема импульсной системы (см. рис. 9.2, в). На рис.

9.3, а приведена схема с нелинейным элементом в цепи обратной связи.

Здесь же, на рис. 9.3, б, показана преобразованная и на рис. 9.3, в приве-

денная структурные схемы исходной нелинейной системы.

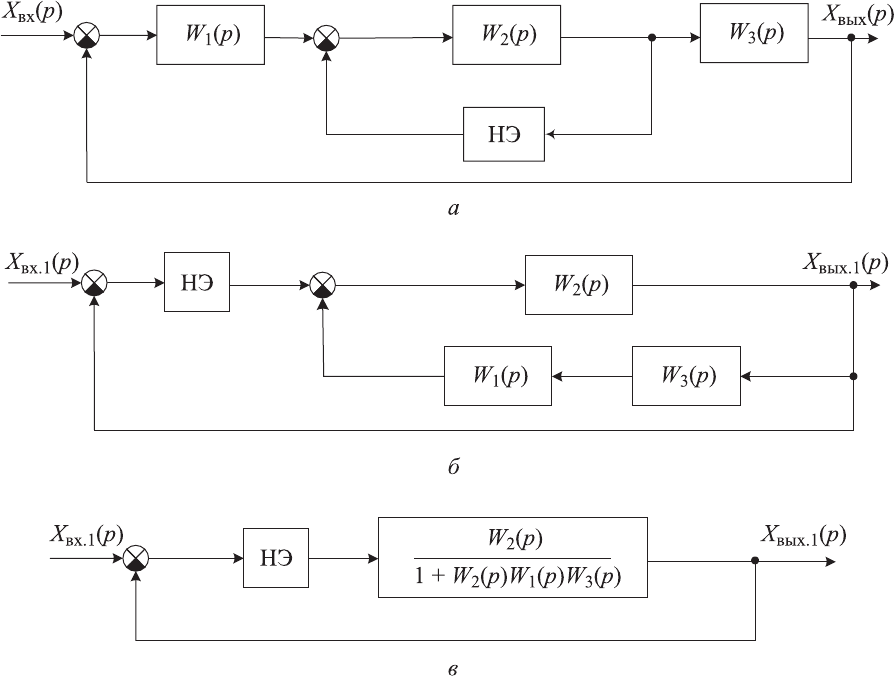
Рис. 9.3. Структурные схемы нелинейной системы с НЭ в обратной связи:

а — исходная; б — преобразованная; в — приведенная

Применяемые на практике нелинейные элементы в зависимости от их

характеристик, устанавливающих связь между входным и выходным сиг-

налами, можно разделить на две группы: элементы с однозначными харак-

теристиками (рис. 9.4, а) и элементы с неоднозначными характеристиками

(см. рис. 9.4, б). Обе эти группы могут в свою очередь подразделяться по

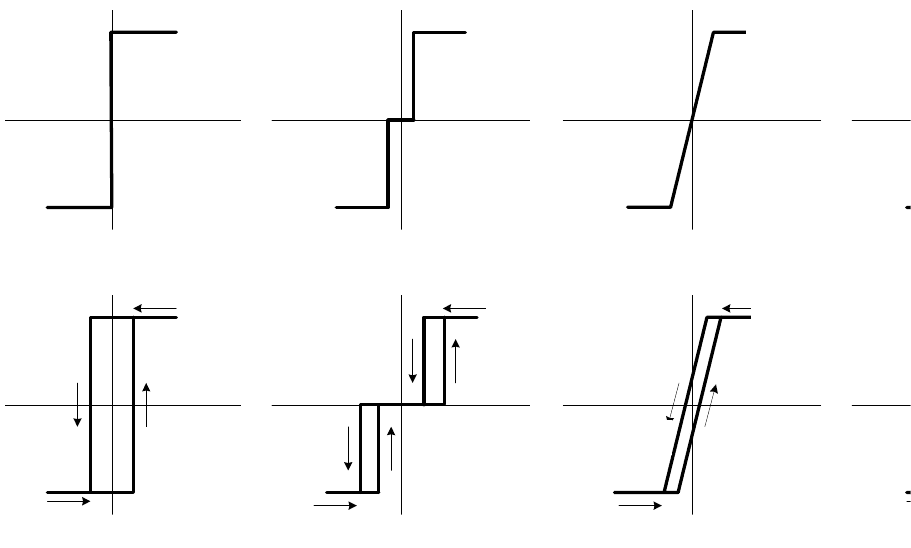
197

другим различным признакам. Особенность неоднозначных характеристик

заключается в том, что выходной сигнал зависит не только от входного

сигнала, но и от его производной.

вых

вх

вых

вх

вых

вх

вых

вх

вых

Рис. 9.4. Характеристики нелинейных элементов:

а — однозначные; б — неоднозначные

Для исследования нелинейной системы автоматического регулирова-

ния необходимо математическое описание ее линейной и нелинейной части.

Математическое описание нелинейной части заключается в установлении

аналитической зависимости между выходным и входным сигналами нели-

нейного элемента в зависимости от вида его характеристики. В табл. 9.1

приведены некоторые характеристики нелинейных элементов и даны анали-

тические зависимости, выражающие

связь между выходным и входным

сигналами.

Рассмотренные нелинейности относятся к классу нелинейностей с ку-

сочно-линейными характеристиками.

вых

вх

вых

вх

198

9.2. ЗАДАЧИ И МЕТОДЫ

ИССЛЕДОВАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ

В связи с тем, что для нелинейных систем характерными и важными

являются вопросы устойчивости, состояния равновесия, возникновения и

существования автоколебаний, то при исследовании динамически нели-

нейных систем возникает необходимость решения таких задач, как:

• отыскание возможных состояний равновесия системы и оценка ее

устойчивости;

• оценка возможности существования автоколебаний и установление

степени их устойчивости;

• выявление соотношений между параметрами, при которых возни-

кают автоколебания;

• определение параметров автоколебаний и их связи с параметрами

системы.

199

Таблица 9.1

Характеристики и аналитическое описание нелинейных элементов

Вид характеристики Аналитическая связь между входом и выходом

вых

−

вх

⎩

⎨

⎧

0при

0,при

вх

вых

х b

вых

вх

b−

−

⎪

⎩

⎪

⎨

⎧

≤

≥

≤ 0при

,||при

,при

вх

вхвх

вх

вых

х b

хахkx

вых

вх

вых

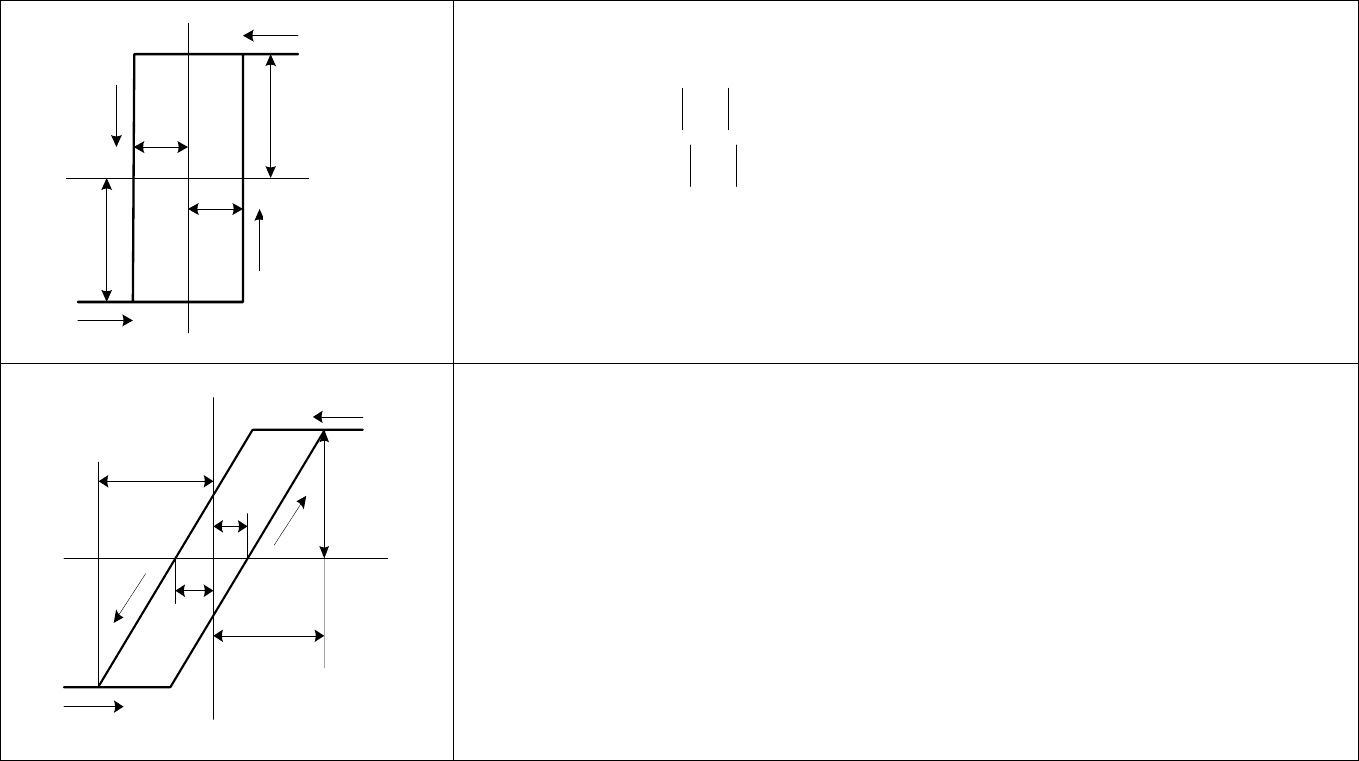
200

Окончание табл. 9.1

вых

вх

b−

−

⎪

⎩

⎪

⎨

⎧

−<

><−

вх

вхвх

вх

вых

0,0,

0,,

х b-

xах

ах b

вых

вх

−

a−

⎪

⎩

⎪

⎨

⎧

≤−

>+≤≤−−

>−≤≤−+

>≤≤+−−

<≤≤−

≥

ах b

хаха b

хаха ахk

хахаа ахk

хахаа b

ах b

2вх

вх12вх2

1вх

вх2вх12

1вх

вх2вх12

2вх

вых

при

0,,2при

0,,2при )(

0,,2 при )(

0,,2при

,при

вх

вых

вх

вых

201

Наличие нелинейных элементов в импульсной системе, естественно,

приводит к описанию процессов в такой системе нелинейными уравнения-

ми, которые в большинстве случаев не решаются в общем виде, и можно

лишь говорить лишь о частных случаях решений. Поэтому при исследова-

нии нелинейных систем важное значение приобретают различные прибли-

женные методы.

В настоящее время

существует большое число различных аналитиче-

ских и графоаналитических методов исследования нелинейных систем, на-

правленных на решение указанных задач. Наиболее существенными из

них, получившими широкое применение в инженерной практике расчета и

проектирования, являются:

1. Метод фазовых траекторий (фазовый);

2. Метод гармонической реализации (баланса);

3. Метод, основанный на критерии абсолютной устойчивости;

4. Метод математического

моделирования.

Использование конкретного метода зависит от структуры исследуе-

мой системы и вида решаемых при этом задач.

9.3. МЕТОД ФАЗОВЫХ ТРАЕКТОРИЙ

Метод фазовых траекторий основан на понятии о фазовом пространстве.

Фазовым пространством

называется многомерное пространство, по

координатным осям которого откладываются значения какой-либо пере-

менной и ее производных соответствующих порядков. Если система регу-

лирования описывается уравнением n-го порядка, то ее состояние можно

рассматривать как задание положения (фазы) некоторой точки, которую

принято называть изображающей точкой

, в n-мерном пространстве. При

изменении состояния системы меняется положение изображающей точки,

и траектория ее перемещения называется фазовой траекторией

Метод фазовых траекторий представляет собой графоаналитический

способ исследования нелинейных систем, сущность которого заключается

в описании поведения систем при помощи наглядных геометрических

представлений — фазовых траекторий (фазовых портретов).

Свободное движение нелинейной системы автоматического регулиро-

вания n-го порядка с одним регулируемым параметром в общем случае

можно описать с помощью n уравнений первого

порядка.

202

Пользование многомерным пространством в практических расчетах

связано с рядом больших аналитических трудностей. В силу этого при

анализе нелинейных систем обычно ограничиваются двумерной фазовой

плоскостью, которая практически позволяет рассматривать поведение сис-

тем, описываемых уравнением не выше третьего порядка или уравнениями

к нему приводимыми. Фазовые траектории этих систем можно построить

непосредственно по дифференциальному

уравнению, не решая его.

Пусть описание системы представлено в виде системы двух уравне-

ний первого порядка:

⎪

⎭

⎪

⎬

⎫

).,(

);,(

yxf

(9.1)

В этих выражениях х — отклонение регулируемого параметра от ус-

тановившегося значения, а y — производная от x. Следовательно,

(x, y) = y. (9.2)

Разделив второе уравнение (9.1) на первое, получим уравнение фазо-

вых траекторий в дифференциальной форме:

yxf

),(

= , (9.3)

в котором независимой переменной является регулируемый параметр, а за-

висимой — его производная.

Разделяя переменные х

и х

и интегрируя уравнение (9.3), получим

уравнение фазовых траекторий в явном виде:

СxFх

= )(

F(x)y

, (9.4)

где С — постоянная интегрирования, зависящая от начальных условий.

Характерные фазовые траектории системы второго порядка приведе-

ны на рис. 9.5.

Построение фазовых траекторий значительно облегчается, если учи-

тывать их следующие свойства, вытекающие из анализа уравнений (9.1)

и (9.3). В верхних квадрантах изображающая точка всегда движется слева

направо, а в нижних — справа налево.