Динкель А.Д. Теория автоматического управления

Подождите немного. Документ загружается.

163

Тогда

1)(σ

раз

ррТ

(р)W

(7.20)

и соответственно для замкнутой системы

1σ

1)(σ1

рТрТ

ррТ

(р)W

. (7.21)

Принимая, что в общем случае

аТ

, (7.22)

запишем передаточные функции для разомкнутого и замкнутого контуров:

1) (σ σ

раз

рра

(р)W

; (7.23)

11)(σ σ

рра

(р)W

. (7.24)

В этих выражениях коэффициент

а определяет быстродействие кон-

тура регулирования и называется коэффициентом демпфирования

. В ко-

нечном итоге все контуры регулирования можно представить эквивалент-

ным инерционным звеном второго порядка с передаточной функцией

(7.24).

С учетом вышепринятого допущения структурная схема любого кон-

тура системы подчиненного регулирования может быть представлена в ви-

де, показанном на рис. 7.2. Согласно этой структурной схеме передаточная

функция разомкнутого контура

(р)W(р)W

0реграз

1 σ

. (7.25)

Тогда из условия равенства правых частей (7.24) и (7.25) получим вы-

ражение для определения передаточной функции регулятора:

(р)рWа

(р)W

рег

. (7.26)

164

7.3. СИНТЕЗ СИСТЕМЫ

ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ

Синтез системы подчиненного регулирования заключается в последо-

вательной оптимизации соподчиненных замкнутых контуров регулирова-

ния, начиная с первого внутреннего и кончая основным внешним. При син-

тезе системы по заданным структуре и параметрам подобъектов регулиро-

вания определяются структура и параметры соответствующих регуляторов.

Под оптимизацией контура регулирования понимается придание конту-

ру таких статических и динамических свойств, при которых

он удовлетворяет

требованиям согласно принятым критериям оптимальности. При этом необ-

ходимо отметить, что оптимизация всех соподчиненных контуров в много-

контурной системе осуществляется по единой методике и выполняется по-

следовательно, начиная с первого внутреннего конура и кончая основным

внешним контуром.

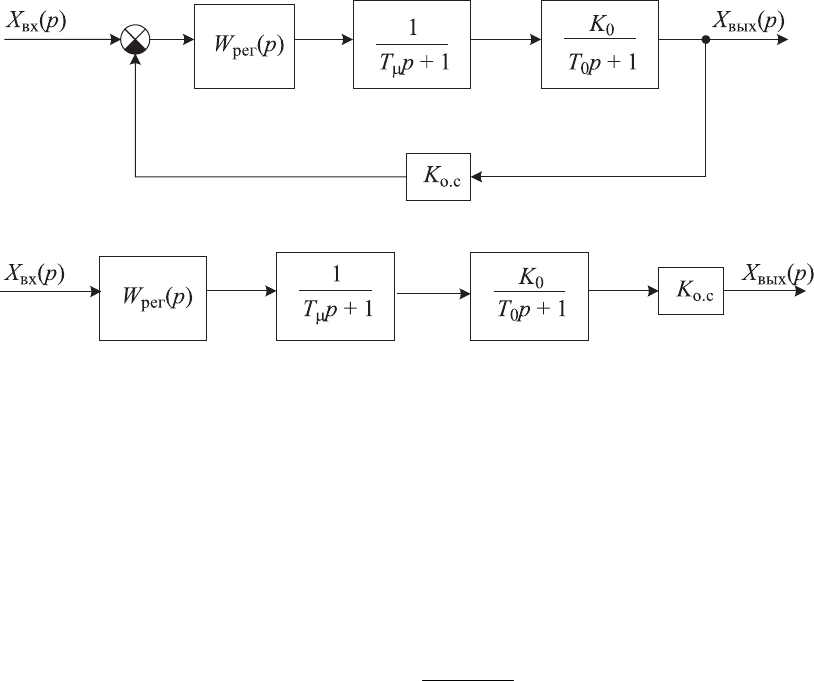
Рис. 7.3. Структурные схемы контура регулирования:

а — замкнутого; б — разомкнутого

Рассмотрим методику синтеза на примере одного контура подчинен-

ного регулирования с учетом определенного критерия оптимальности.

В структурной схеме контура подчиненного регулирования, приведенной

на рис. 7.3,

а, объект регулирования представлен звеном с малой неком-

пенсируемой постоянной и единичным передаточным коэффициентом

н.к

рТ

(р)W

(7.27)

165

и объектом компенсации

о.к

рТ

(р)W

. (7.28)

При этом имеется в виду, что обратная связь в контуре не единичная.

Для определения передаточной функции регулятора по вышеизло-

женной методике исходную структурную схему необходимо представить в

виде разомкнутой структурной схемы с выходом по сигналу обратной свя-

зи, как это показано на рис. 7.3,

б.

Исходя из структурной схемы, некомпенсируемая постоянная времени

Т ,

а передаточная функция расчетного объекта компенсации запишется в

следующем виде:

о.к

рТ

(р)W

о.с

. (7.29)

Подставив эти данные в (7.26), получим передаточную функцию регу-

лятора

о.с0µ

рег

KрKаТ

рТ

(р)W

= . (7.30)

Полученное выражение позволяет определить структуру регулятора, а

для определения параметров регулятора необходимо знать значение коэф-

фициента демпфирования

а.

Передаточная функция замкнутого контура, учитывая (7.30), с выхо-

дом по сигналу обратной связи запишется в следующем виде:

вх

о.с

раТраТ

(р)Х

(р)W

(7.31)

Из этого следует, что динамические свойства контура при заданном

значении некомпенсируемой постоянной времени

зависят только от ко-

эффициентов демпфирования. Он может быть определен из условия обес-

печения оптимального переходного процесса.

166

В системах подчиненного регулирования за оптимальный принимает-

ся переходный процесс в идеальном фильтре, при котором достигается

максимальное быстродействие, т. е. минимальное время регулирования,

при перерегулировании, не превышающем 20 %. Такой оптимум динами-

ческого процесса называется техническим

или модульным.

Применительно к этому оптимуму желаемая передаточная функция

системы второго порядка, исходя из нормированной, будет иметь следую-

щий вид:

11,4

вх

о.с

рр

(р)Х

(р)W

. (7.32)

Тогда, из условия

(р)W(р)W

жз

, (7.33)

получим равенства

а 1

=Т ; (7.34)

а 1,4

Т , (7.35)

из которых следует, что

а = 1,4

≈

2. (7.36)

Таким образом, из условия принятого оптимума динамического про-

цесса получено конкретное значение коэффициента демпфирования кон-

тура регулирования, в соответствии с которым определяются параметры

регулятора.

Далее необходимо отметить, что при оптимизации какого-либо внеш-

него контура по отношению к одному или ряду внутренних контуров, в

полиноме знаменателя передаточной функции не учитываются

члены

высшего порядка от

р, а учитывается лишь член первого порядка, т. е. пе-

редаточная функция внутренних контуров

()

вн

caT p

, (7.37)

где

с — целое число, зависящее от количества внутренних контуров.

167

7.4. ОГРАНИЧЕНИЕ РЕГУЛИРУЕМОГО

ПАРАМЕТРА И ЕГО ПРОИЗВОДНОЙ

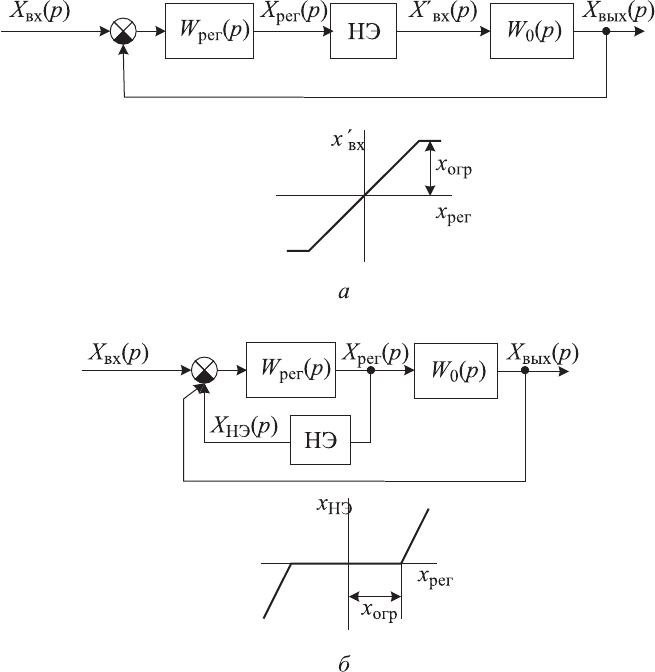
Принцип ограничения регулируемого параметра, т. е. сигнала на вы-

ходе контура регулирования, основан на ограничении сигнала на входе

контура объекта регулирования, которым является выходной сигнал регу-

лятора. Реализовать этот принцип можно введением в контур регулирова-

ния нелинейного элемента с соответствующей характеристикой. При этом

возможны два варианта включения нелинейного элемента, которые пред

ставлены на рис. 7.4. В первом варианте используется нелинейный элемент

(НЭ) с линейно-ограниченной характеристикой, а во втором элемент с зо-

ной нечувствительности в его характеристике.

Рис. 7.4. Схемы вариантов ограничения выходного параметра

В реальных системах подчиненного регулирования возникает необхо-

димость ограничения производной (скорости изменения) регулируемого

168

(выходного) параметра какого-то контура регулирования. Это ограничение

может осуществляться тремя принципиально различными способами.

Первый способ основан на введении в систему дополнительного кон-

тура регулирования производной соответствующего регулируемого пара-

метра. Реализация этого способа, как правило, связана с измерением про-

изводной регулируемого параметра. Как известно, операция дифференци-

рования в системах регулирования

нежелательна. В связи с этим в реаль-

ных системах подчиненного регулирования этот способ ограничения про-

изводной регулируемого параметра практически не применяется.

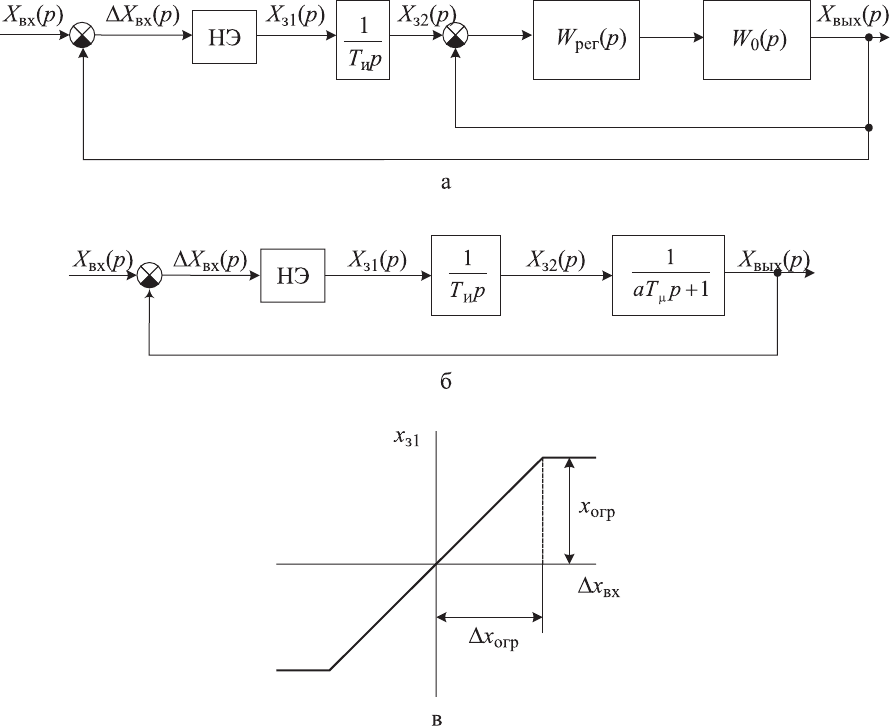
Второй способ, как и первый, основан на введении в структуру систе-

мы подчиненного регулирования дополнительного контура, в структуру

которого входит нелинейный элемент с линейно ограниченной характери-

стикой и интегрирующее

звено, как это показано на рис. 7.5, а.

Рис. 7.5. Структурные схемы системы с контуром ограничения производной

регулируемого параметра:

а — исходная; б — преобразованная;

в — характеристика нелинейного элемента

169

После оптимизации внутреннего контура по выше изложенной мето-

дике, его можно представить в виде динамического звена с передаточной

функцией

раТ

(р)W

. (7.38)

Соответственно исходная структурная схема преобразуется к виду,

представленному на рис. 7.5,

б.

Рассматриваемая система подчиненного регулирования с ограничени-

ем производной выходного сигнала работает в двух режимах в зависимо-

сти от величины

вх

∆х (см. рис. 7.5, в):

Когда

огрвх

∆∆ хх ≥ , на выходе НЭ будет постоянный сигнал, рав-

ный

огр

х , т. е. на вход интегрирующего звена будет поступать постоянный

по величине сигнал

const

огрз1

хх ,

т. е. система регулирования фактически будет разомкнутой. В этом случае,

из-за постоянства

з1

сигнал на выходе интегрирующего звена х

з2

изменя-

ется линейно в функции времени. Темп изменения этого сигнала определя-

ется постоянной времени интегрирующего звена

. Соответственно с та-

ким же темпом будет изменяться выходной сигнал

вых

Когда

огрвх

∆∆ хх ≥ , нелинейный элемент работает на линейном

участке. При этом система регулирования становится замкнутой по внеш-

нему контуру, обеспечивая отработку входного сигнала

вх

(t). На линей-

ном участке НЭ характеризуется передаточным коэффициентом

огр

∆

НЭ

= . (7.39)

Во втором режиме с учетом

и K

НЭ

передаточная функция системы

1)(

НЭНЭ

НЭ

µи

вх

вых

аТ

раТрТ

(р)Х

(р)W

. (7.40)

170

Потребуем, чтобы замкнутая система регулирования с нелинейным

контуром при работе нелинейного элемента на линейном участке была эк-

вивалентна обычной двухконтурной системе подчиненного регулирования

µ1

раТраТ

(р)W

, (7.41)

где

µµ1

аТТ = .

Из условия равенства коэффициентов полиномов знаменателей (7.40)

и (7.41) получим

µ1

НЭ

ТааТ

. (7.42)

Исходя из передаточной функции интегрирующего звена

рТ(р)Х

(р)Х

(р)W

из1

з2

== , (7.43)

получим

(р)Х

(р)рХ

з1

з2

= . (7.44)

Переходя в (7.44) от изображений к оригиналам, связь между

з1

(t) и

з2

(t) запишем в следующем виде

(t)х

з1

з2

= . (7.45)

Тогда постоянная времени интегрирующего звена

(

)

()

з1

з2

dx t

= . (7.46)

Для момента перехода системы из второго режима в первый можно

записать следующие равенства:

огрз1

хх

;

выхз2

хх

171

Задавшись значением

огр

нелинейного элемента и при заданном зна-

чении ограничения производной выходного сигнала

огр

вых

⎟

⎠

⎞

⎜

⎝

⎛

(t)х

, полу-

чим выражение для определения постоянной времени интегрирующего

звена

огр

вых

огр

⎟

⎠

⎞

⎜

⎝

⎛

(t)х

Т (7.47)

Определив по этому выражению Т

, из (7.42) получим, что передаточ-

ный коэффициент нелинейного элемента на его линейном участке

НЭ

Та

K =

. (7.48)

Таким образом, выражения (7.47) и (7.48) позволяют определить тре-

буемые Т

и K

НЭ

, при которых обеспечивается требуемое ограничение

производной регулируемого выходного сигнала при работе системы регу-

лирования в первом режиме и адекватность рассматриваемой нелинейной

системы оптимизированной линейной двухконтурной системе при работе

во втором режиме.

Данный способ применяется как для ограничения производной вы-

ходного регулируемого параметра, так и для ограничения любого проме-

жуточного параметра

в системе регулирования, например ограничения

скорости изменения тока в различных системах автоматизированного

электропривода.

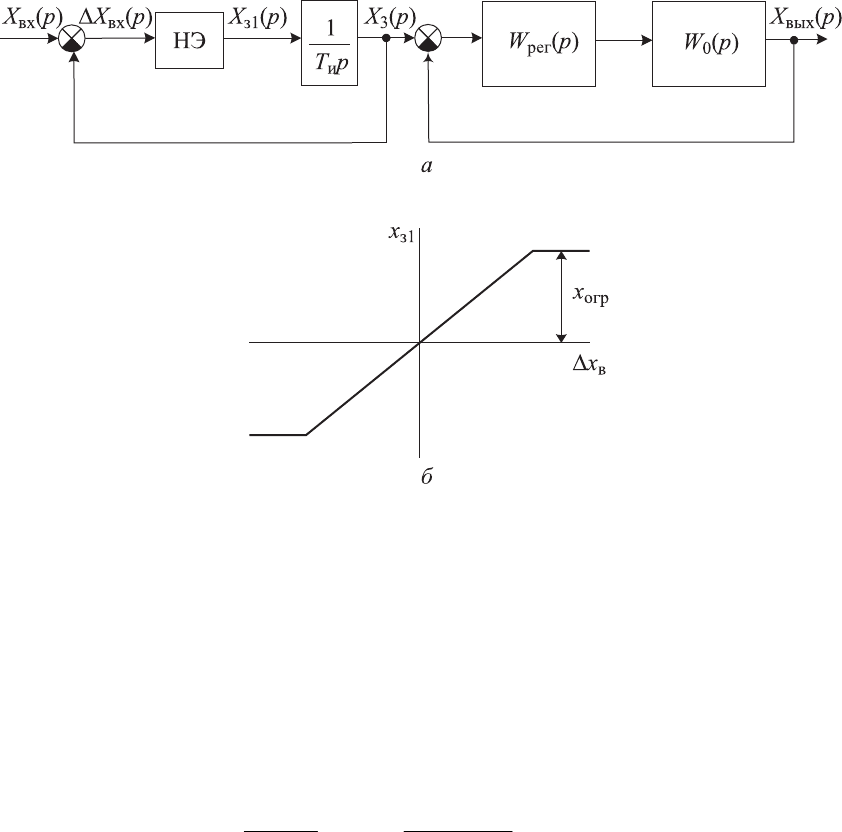
Третий способ основан на ограничении производной задающего сиг-

нала на входе основной системы регулирования выходного параметра

вых

(t). Этот способ реализуется с помощью так называемого задатчика ин-

тенсивности, как это показано на рис. 7.6. Как видно из структурной схе-

мы, задающий сигнал Х

(р) на входе основной системы регулирования вы-

ходного параметра формируется нелинейным контуром регулирования.

172

Рис. 7.6. Структурная схема системы с ограничением производной

задающего сигнала и характеристики нелинейного элемента

Расчет этого контура регулирования заключается в определении по-

стоянной времени интегрирующего звена и передаточного коэффициента

нелинейного элемента на его линейно-ограниченном участке. Для этого

необходимо задать значение х

огр

, исходя из реальных возможностей, и по

формуле (7.47) при заданном постоянном темпе изменения

огр

⎟

⎠

⎞

⎜

⎝

⎛

(t)х

⎟

⎠

⎞

⎜

⎝

⎛

tх

)( d

вых

= const

определить постоянную времени интегрирующего звена Т

и далее по

формуле (7.48) определить значение нелинейного элемента K

НЭ

Необходимо отметить, что данный способ используется в основном

для ограничения темпа изменения выходного параметра системы автома-

тического регулирования, например для ограничения или задания опреде-

ленного темпа разгона электропривода. При этом основная система авто-

матического регулирования выходного сигнала может представлять собой

систему подчиненного регулирования с любым количеством соподчинен-

ных контуров регулирования.