Динкель А.Д. Теория автоматического управления

Подождите немного. Документ загружается.

213

9.5. РЕЖИМ АВТОКОЛЕБАНИЙ

И УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ

Применительно к нелинейным системам автоматического регулиро-

вания существует два понятия — устойчивость автоколебаний и устойчи-

вость равновесного состояния.

Под устойчивостью режима автоколебаний понимается такой режим

автоколебаний, который физически осуществим в системе и устойчиво

удерживается при возможных отклонениях его как по амплитуде, так и по

частоте, возникающих по какой либо причине.

Если известны

передаточная функция линейной части

(

)

()

, (9.29)

где I

(р), R

(р) — полиномы числителя и знаменателя эквивалентная пере-

даточная функция нелинейной части (9.25), то эквивалентная передаточная

функция разомкнутого и замкнутого контуров нелинейной системы соот-

ветственно будут следующими:

⎥

⎦

⎤

⎢

⎣

⎡

+= )(

)(

ω),,(

м1м

хq

хpW

, (9.30)

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

)(

)()()(

)(

)()(

ω),,(

м1млл

м1мл

хq

хqpIpR

хq

хqpI

хpW

. (9.31)

В режиме автоколебаний амплитуда х

и частота

будут постоянны-

ми. Следовательно, и передаточная функция системы как в разомкнутом,

так и в замкнутом состоянии также постоянная, а выражения (9.29) и (9.30)

линейны и их можно анализировать методами теории линейных систем ав-

томатического регулирования.

Условием существования в нелинейной системе установившихся ав-

токолебаний вида

214

tхtх

ωsin )(

м.авых

(9.32)

с постоянной амплитудой х

м.а

и частотой автоколебаний ω

является нахо-

ждение нелинейной линеаризованной системы на колебательной границе

устойчивости. Эта граница может быть определена на основе любого из

критериев устойчивости линейных систем автоматического регулирова-

ния. Наиболее удобными для определения колебательной границы устой-

чивости являются частотные методы Михайлова и Найквиста.

Комплексные частотные характеристики разомкнутой и замкнутой

системы при условии существования

автоколебаний, исходя из (9.30) и

(9.31) запишутся в следующем виде:

[]

)()(

)ω(

)ω,(

м.a1м.a

aл

ам.а

хjqхq

jхW

+= ; (9.33)

[

]

[]

)()()(ω)ω(

)()()ω(

)ω,(

м.a1м.aaлaл

м.a1м.aaл

aм.аз

хjqхqIjR

хjqхqjI

jхW

= . (9.34)

Приравняв знаменатель (9.34) к нулю, получим уравнение характери-

стической кривой Михайлова:

[

]

0)()()(ω)ω(

м.a1м.aaлaл

+ хjqхqIjR , (9.35)

которая проходит через начало координат при конкретных значениях х

м.а

, что и будет соответствовать условию существования автоколебаний в

системе.

Выделив в левой части (9.35) вещественную и мнимую составляющие,

получим систему двух уравнений:

⎭

⎬

⎫

0.)ω,(

0;)ω,(

ам.а

хQ

хP

(9.36)

Выполнение этих равенств соответствует прохождению характери-

стической кривой через начало координат, а следовательно, получаемые

значения х

м.а

и ω

в результате решения (9.36) и будут параметрами авто-

колебательного режима в нелинейной системе.

Если уравнения (9.36) не имеют положительных действительных кор-

ней х

м.а

и ω

, то автоколебания в системе невозможны.

215

Полученные в результате решения (9.36) значения х

м.а

и ω

необходимо

проверить, соответствуют ли они устойчивым автоколебаниям в системе.

Для этого используется следующее условие устойчивости автоколебаний:

ωω

м.aаaм.а

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

−

⎟

⎠

⎞

⎜

⎝

⎛

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

QPQ

. (9.37)

При этом в (9.37) необходимо подставить числовые значения х

м.а

и ω

полученные в результате решения (9.36).

Данный метод определения параметров устойчивых автоколебаний в

нелинейной системе автоматического регулирования приемлем при отно-

сительно невысоком порядке дифференциального уравнения, описываю-

щего динамические процессы в линейной части системы, ввиду сложности

или невозможности решения системы уравнений (9.36). Если линейная

часть описывается дифференциальным уравнением высокого порядка или

включает в себя

элемент запаздывания, то для выявления параметров авто-

колебаний и их устойчивости можно воспользоваться критерием устойчи-

вости Найквиста.

Согласно этому критерию система автоматического регулирования на-

ходится на границе устойчивости, если амплитудно-фазовая характеристика

разомкнутой системы проходит через точку с координатами (–1, j0). Следо-

вательно, условием существования автоколебаний является равенство

1)()

ω(

м.анл

−

хWjW , (9.38)

где

()

(

)

()

ал

jW = ; )()()(

м.а1м.ам.ан

хjqхqхW

или

()

м.ан

ал

хW

jW −=

. (9.39)

Левая часть уравнения (9.39) представляет собой амплитудно-фазовую

характеристику линейной части системы, а правая — обратную характери-

стику нелинейного элемента, взятую с противоположным знаком.

Уравнение (9.39) удобно решать графически. Для этого указанные ха-

рактеристики необходимо построить в одной системе координат (рис. 9.10),

отмечая при этом на кривой ω)(

jW частоту колебаний ω

, а на кривой

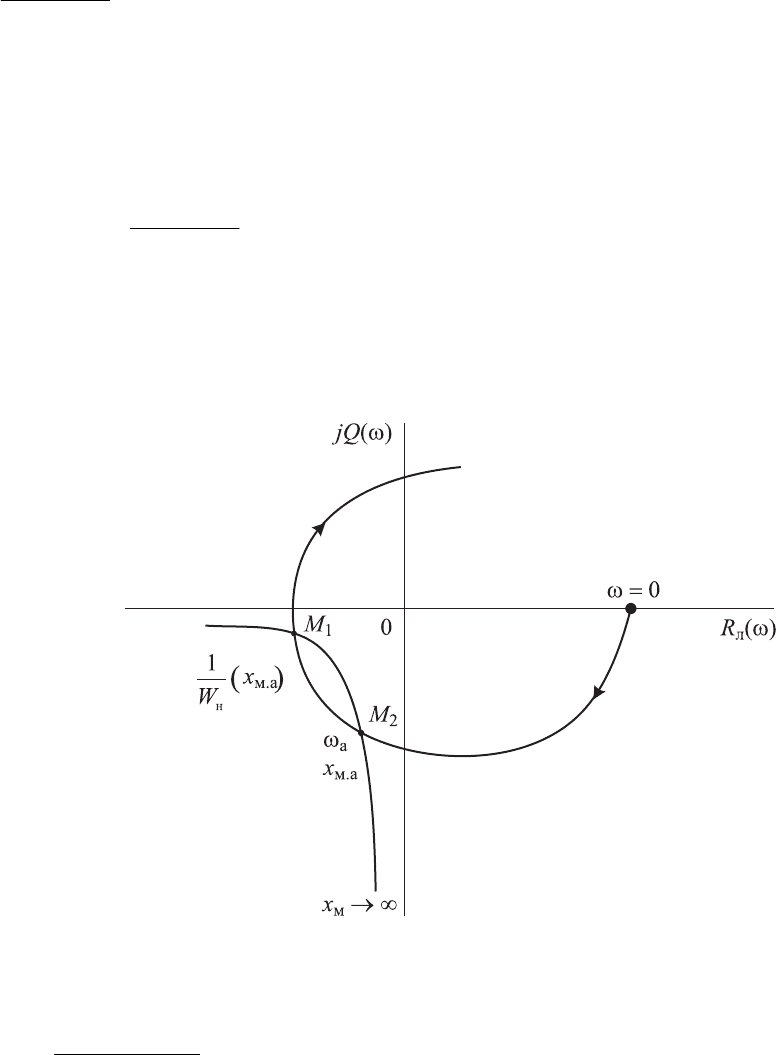
216

)(

м.а

хW

амплитуду колебаний х

м.а

. В точках пересечения этих характе-

ристик выполняется условие (9.39). Если характеристики не пересекаются,

то автоколебания отсутствуют.

Точка пересечения характеристик, соответствующая режиму устойчи-

вых автоколебаний, устанавливается по следующему правилу: если точка

на кривой

)(

м.ан

хW

, близкая к точке пересечения, но сдвинутая в направ-

лении возрастания параметра х

м.а

, не охватывается кривой ω)(

jW , то ав-

токолебания устойчивы с параметрами х

м.а

и ω

(точка М

), если же охва-

тывается, то неустойчивы (точка М

Рис. 9.10. Определение амплитуды и частоты автоколебаний

Пример 9.2. Определим амплитуду и частоту автоколебаний в нели-

нейной системе автоматического регулирования (рис. 9.11) на основе кри-

терия Михайлова при следующих параметрах:

= 1, Т

= 2 с, Т

= 0,5 с, с = 1, b = 0,5.

Согласно структурной схеме, приведенной на рис. 9.11, передаточная

функция разомкнутой и замкнутой систем на основе (9.30) и (9.31) соот-

ветственно равны:

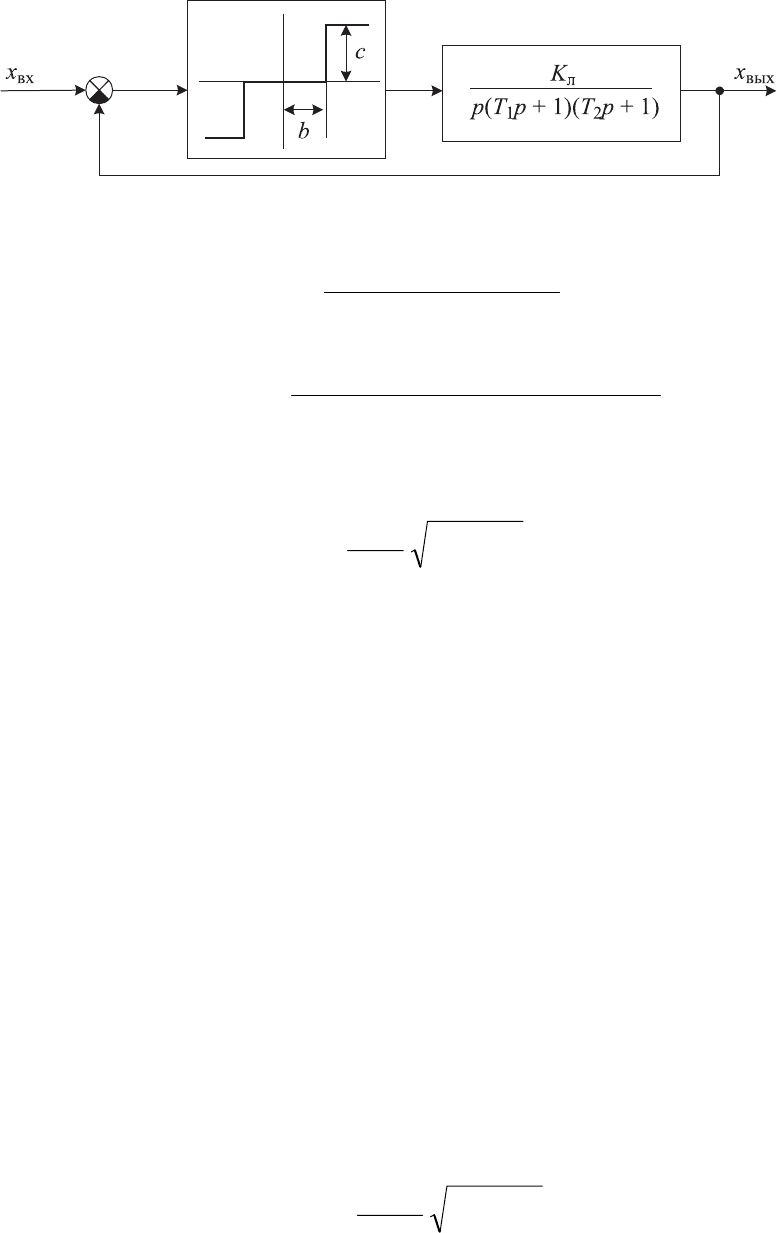
217

Рис. 9.11. Структурная схема нелинейной системы

)(

1)1)((

ω),,(

хq

рТрТр

хрW

, (9.40)

)(1)1)(

)(

ω),,(

мл21

мл

мз

хqKрТрТр

хqK

хрW

+++

(

. (9.41)

В соответствии с табл. 9.1 для принятого типа нелинейного элемента

)( bх

хq −= ; (9.42)

Исходя из (9.41), характеристическое уравнение замкнутой системы

имеет вид

0)()(

мл

=++++ хqKррТТрТТ

. (9.43)

Подставив в (9.43) р = jω, получим

0)(ω)ω(ω

=+++−− хqjТТТjТ

. (9.44)

Тогда вещественную и мнимую части (9.44) можно записать так:

⎪

⎭

⎪

⎬

⎫

−−=

++−=

1).ωω()ω,(

),()ω()ω,(

21ам

мл

21ам

ТТхQ

хqKТТхP

(9.45)

Приравнивая выражения (9.45) к нулю и подставляя в них (9.42), по-

лучим следующую систему уравнений:

⎪

⎭

⎪

⎬

⎫

=−

=−++−

0.1ω

)ω

а21

ТТ

bх

сK

ТТ(

(9.46)

218

Из второго уравнения системы (9.46) частота автоколебаний

с 1

0,52

−

⋅

ТТ

. (9.47)

Подставляя в первое уравнение (9.46) частоту ω

(9.47), его можно

привести к виду

=+− ВуАу , (9.48)

где

ху =

лк

⎟

⎠

⎞

⎜

⎝

⎛

ТТ

Корни этого уравнения

Аb

411

1,2

−±

=у

. (9.49)

Подставляя в (9.49) исходные данные, с учетом принятых обозначе-

ний получим

1,23

0,871

1,2

=у

Следовательно,

1,27

м1

х и 0,316

м2

х .

Так как (9.42) справедливо при bх >

, то окончательно принимаем

значение амплитуды колебаний

1,27

м1м.а

хх .

Для того чтобы установить устойчивость колебаний при полученных

значениях частоты

с 1

−

=ω

и амплитуды

27,1

м1

, применим общее ус-

ловие устойчивости автоколебаний (9.37). В данном случае имеем

219

⎪

⎭

⎪

⎬

⎫

−=

∂

+−=

∂

−

∂

.ω31

;)ω2(

;

)(24

а21

a21

ТТ

bхх

хbсK

(9.50)

Подставляя значения частных производных (9.50) в условие (9.37) и

учитывая одновременно выражение (9.47), получим

)(28

−

bхх

хbсK

(9.51)

или

0,71

>х .

Это условие в данном случае выполняется, а следовательно автоколе-

бания с частотой

c 1ω

−

= и амплитудой 1,27

а м.

х будут устойчивыми.

Пример 9.3.

Определим амплитуду и частоту автоколебаний в нели-

нейной системе автоматического регулирования (рис. 9.12) на основе кри-

терия Найквиста при следующих параметрах:

= 2, Т = 0,5 с, с = 1, b = 0,5.

Рис. 9.12. Пример структурная схемы нелинейной системы

Исходя из передаточной функции линейной части разомкнутой систе-

мы, ее амплитудно-фазовая частотная характеристика

220

)ω(

ωω

ω)(

−=

+−

jТ

. (9.52)

Соответственно вещественная и мнимая составляющие этой характе-

ристики запишутся в следующем виде:

⎪

⎭

⎪

⎬

⎫

1ω

) (ω

;

1ω

) (ω

ТK

(9.53)

Согласно табл. 9.1 отрицательная обратная характеристика нелиней-

ного элемента

⎟

⎠

⎞

⎜

⎝

⎛

+−−=

−−

−=−

jbbх

сK

jbх

хW

мн

)(

.(9.54)

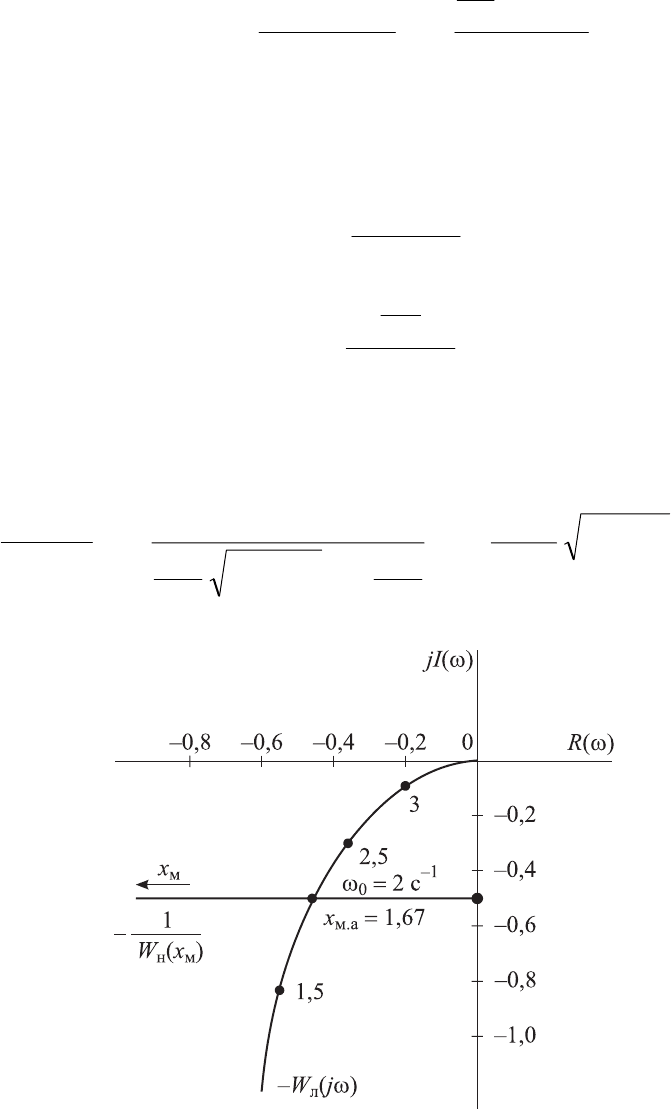
Рис. 9.13. Определение амплитуды и частоты автоколебаний

на основе критерия Найквиста

221

Соответственно вещественная и мнимая составляющие этой характе-

ристики запишутся в следующем виде:

⎪

⎭

⎪

⎬

⎫

−=

−−=

.)(

;

)(

мн

bхI

bх

сK

хR

(9.55)

Графическое решение поставленной задачи на основе (9.53) и (9.55)

при исходных данных приведено на рис. 9.13. Здесь показаны графики ам-

плитудно-фазовой характеристики линейной части ω)(

jW и обратная от-

рицательная характеристика нелинейного элемента

)(

мн

хW

− . Точка пере-

сечения этих характеристик определяет частоту ω

и амплитуду х

м.а

авто-

колебаний в нелинейной системе. В данном случае автоколебания устой-

чивые, так как точка на характеристике

)(

мн

хW

−

, близкая к точке пересе-

чения, сдвинутая в направлении увеличения

, не охватывается характе-

ристикой ω)(

jW .