Динкель А.Д. Теория автоматического управления

Подождите немного. Документ загружается.

(

)

(

)

),(

)(

вх1

вых1

pХ bpb...pbpb

pХcpc...pcpc

++++=

=++++

−

(1.7)

где )( ),(

выхвх

pХpХ — изображения входного и выходного сигналов.

Полученное уравнение (1.7) является изображением исходного линей-

ного дифференциального уравнения (1.4) при нулевых начальных услови-

ях. Как видно из сравнения (1.4) и (1.7), для того чтобы линейное диффе-

ренциальное уравнение представить в операторной форме, необходимо

сделать подстановку

и функции х

вх

(t) и х

вых

(t) заменить их изображениями )( ),(

выхвх

pХpХ .

1.2.2. Статические и динамические характеристики

Для анализа процессов, протекающих в системе автоматического ре-

гулирования, необходимо знать статические и динамические характери-

стики как самой системы автоматического регулирования, так и отдельных

элементов (звеньев), на основе которых построена эта система.

Статические характеристики элементов или системы устанавливают

связь между выходными и входными сигналами в установившемся режи-

ме, то есть при

t → ∞. Статика системы регулирования определяет харак-

теристику установившихся состояний

вых

= f(х

вх

). (1.8)

Эта зависимость может быть как линейной, так и нелинейной. Боль-

шое количество характеристик реальных элементов и систем может быть

нелинейным. Во многих случаях нелинейные характеристики можно заме-

нить эквивалентными (приближенными) линейными характеристиками, не

допуская при этом погрешностей, превышающих допустимые пределы.

Например, если нелинейная характеристика представляет собой линейно

ограниченную функцию, то

систему с такой характеристикой представля-

ют как линейную, если рабочий диапазон изменения сигналов не выходит

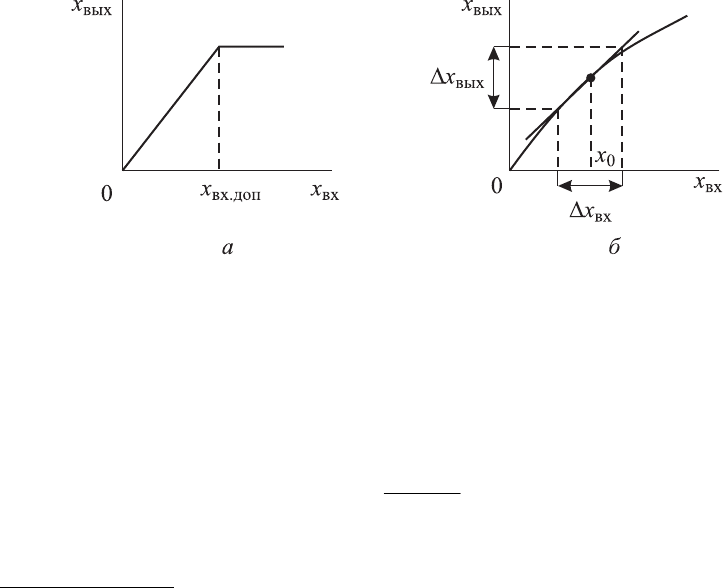
за пределы линейного участка (рис. 1.4, а). Если нелинейная характеристи-

ка представляет собой непрерывно дифференцируемую функцию, как это

показано на рис. 1.4, б, то в окрестности рабочей точки в определенном ог-

раниченном диапазоне изменения входного и выходного сигналов нели-

нейную характеристику можно заменить линейной

вых

= K х

вх.

Рис. 1.4. Линеаризация нелинейных статических характеристик

При этом коэффициент K определяется по наклону касательной, про-

веденной к исходной характеристике в рабочей точке, соответствующей

установившемуся режиму.

вх

вых

∆

K =

. (1.9)

Динамические

характеристики устанавливают аналитическую (функ-

циональную) связь между выходным и входным параметрами системы в

динамике, т. е. в переходных режимах

вых

(t) = f х

вх

(t). (1.10)

Эта зависимость описывается линейным или нелинейным дифференциаль-

ным уравнением.

Для линейных систем динамические характеристики вида (1.10) полу-

чаются в результате решения линейных дифференциальных уравнений.

Применительно к системам автоматического регулирования, в струк-

туре которых имеются нелинейные элементы, для установления динамиче-

ских характеристик необходимо решать нелинейные дифференциальные

уравнения, что связано с определенными

трудностями. С целью упроще-

ния анализа нелинейных систем используется метод линеаризации нели-

нейности нелинейного элемента, как это показано выше, в результате чего

при малых изменениях х

вх

(t), не выходящих за пределы ∆х

вх

динамические

процессы можно описать линейными дифференциальными уравнениями

устанавливающими связь между отклонениями выходных и входных сиг-

налов относительно значений х

. В результате решения полученного таким

образом дифференциального уравнения в отклонениях (вариациях), полу-

чается динамическая характеристика системы, связывающая отклонение

выходного и входного сигналов относительно их установившихся значе-

ний, соответствующих определенному значению сигнала на входе системы

вх. 0

, которую можно записать в виде

∆х

вых

=f ∆ х

вх

(t), при х

вх 0

= const. (1.11)

Допустимость такой линеаризации нелинейной системы автоматиче-

ского регулирования определяется характеристиками нелинейных элемен-

тов и весьма ограничена. Эта линеаризация применима только для малых

отклонений и при непрерывно дифференцируемых характеристиках нели-

нейных звеньев, называемых линеаризуемыми.

1.2.3. Передаточная функция и структурная схема

Передаточной функцией звена или системы называется отношение

изображения выходной величины к изображению входной величины. При

этом принимаются нулевые начальные условия. Следовательно, переда-

точная функция определяется в виде отношения

(p)Х

(p)X

W(p)

вх

вых

= , (1.12)

где

вых

(p) = L [X

вых

(t)] и Х

вх

(p) = L [X

вх

(t)].

Если имеется линейное дифференциальное уравнение, описывающее

динамические процессы:

вых вых вых

вых

01 1

вх вх вх

вх

01 1

[()] [()] [()]

... ( )

[()] [()] [()]

... ( ),

−

++ + =

=+ ++ +

dx t d x t dx t

cc c cxt

dxt d xt dxt

bb b bxt

(1.13)

то, как показано выше, путем подстановки оператора

получаем

уравнение, представленное в операторной форме:

()

01 1 вых

01 1 вх

...

−

++++ =

++++

cp cp c p c x p

bp bp b p b x p

. (1.14)

Исходя из (1.12) и (1.14) передаточная функция

М(р)

(р) Е

cpc...pc

bpb...pbpb

(p)Х

(p)X

W(p)

++++

−

вх

вых

. (1.15)

М(р)(р)

, — полиномы числителя и знаменателя передаточной функции.

В реальных системах всегда

m ≤ n.

Приравняв полиномы числителя и знаменателя к нулю, получим соот-

ветствующие алгебраические уравнения

m-го и n-го порядка относительно р:

=++++

−

bpb...pbpb

, (1.16)

=++++

−

cpc...pcpc

. (1.17)

Корни уравнения (1.16) называются нулями.

Уравнение (1.17) называется характеристическим уравнением, а его

корни — полюсами.

Структурной схемой системы автоматического регулирования назы-

вается схема, в которой входящие в нее звенья представлены в виде пря-

моугольников с указанными в них соответствующими передаточными

функциями и соединены стрелками, показывающими связь между звенья-

ми и направление прохождения сигналов.

Стрелками также указываются

входные и выходные сигналы. Структурная схема системы, как правило,

строится на основе функциональной или алгоритмической схемы.

1.2.4. Переходная функция

Функция, отражающая изменение выходного сигнала звена или сис-

темы автоматического регулирования в зависимости от времени при пода-

че на вход сигнала в виде ступенчатой функции, называется переходной

функцией или переходным процессом.

Ступенчатой функцией называется функция, которая мгновенно воз-

растает от нуля до какого-то значения и значение которой с течением вре

мени остается постоянным:

()

⎪

⎩

⎪

⎨

⎧

≥

0.приconst

0;при0

вх

tх (1.18)

Переходную функцию можно определить по изображению выходно-

го сигнала Х

вых

(р), воспользовавшись обратным преобразованием Лапла-

са (1.3):

вых

(t) =L

–1

[Х

вых

(p)]. (1.19)

Частным случаем ступенчатой функции является единичная ступенча-

тая функция. Единичной ступенчатой функцией называется функция, ко-

торая мгновенно возрастает от нуля до единицы:

[

]

вх

(t)х . (1.20)

При подаче на вход звена или системы входного сигнала в виде еди-

ничной ступенчатой функции выходной сигнал представляет собой пере-

ходную характеристику h(t) звена или системы.

Согласно выражению для передаточной функции (1.12) и табл. 1.1 при

воздействии единичной входной ступенчатой функции получим

W(p)

(p)Х

вых

, (1.21)

с учетом (1.19) из (1.21) следует, что

⎥

⎦

⎤

⎢

⎣

⎡

−

W(p)

Lh(t)

. (1.22)

Исходя из (1.22) переходную функцию или переходный процесс мож-

но получить путем умножения переходной характеристики на значение

ступенчатой функции, отличной от единичной.

Переходные процессы в устойчивых системах, описываемые переход-

ными функциями, крайне разнообразны. Однако их можно разбить на сле-

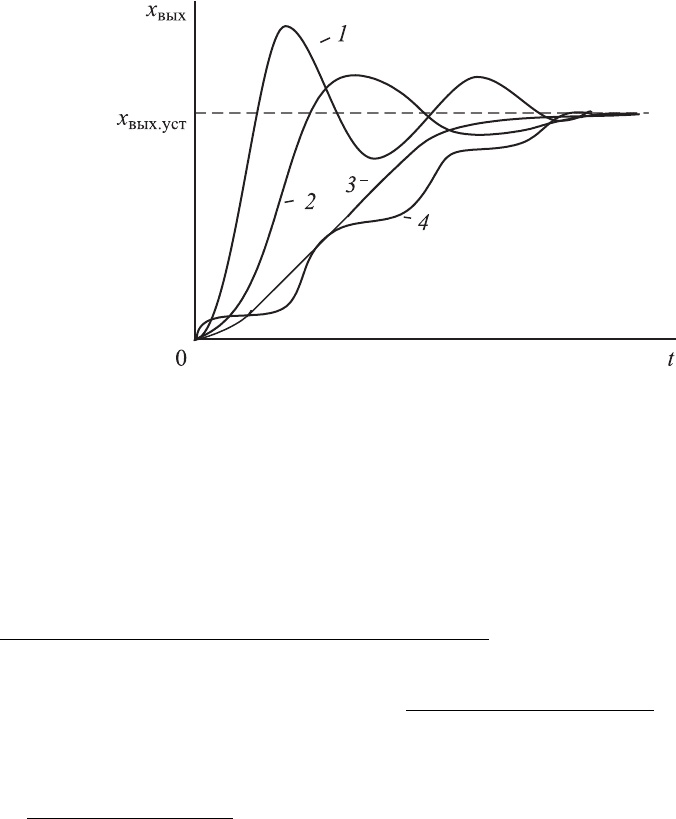
дующие четыре основных вида (рис. 1.5):

Колебательные, в которых производная меняет знак теоретически

бесконечное число раз.

Малоколебательные, в которых производная меняет знак два раза;

Монотонные колебательные, в которых производная может изме-

нять знак, но переходная функция не превышает своего

установившегося значения.

Монотонные, в которых производная не меняет знак и постепенно

уменьшается по мере приближения переходной функции к устано-

вившемуся значению.

Рис. 1.5. Виды переходных процессов:

1 — колебательные; 2 — малоколебательные;

3 — монотонноколебательные; 4 — монотонные

Наряду с переходной характеристикой, для оценки динамических

свойств звеньев и системы автоматического регулирования используется

импульсная переходная характеристика (весовая функция).

Импульсная переходная характеристика

w(t) отражает изменение вы-

ходного сигнала в функции времени при воздействии на систему входного

сигнала в виде единичного импульса. Единичный импульс

— это импульс,

площадь которого равна единице при длительности, стремящейся к нулю,

и высоте, стремящейся к бесконечности. Такой единичный импульс назы-

вается дельта-функцией

и обозначается δ(t). Математически это можно за-

писать так:

()

⎪

⎩

⎪

⎨

⎧

≤

=∞

0.при0

0;при

(1.23)

При этом согласно определению

∫

∞

∞−

= 1 )dδ( tt .

Дельта-функция просто связана с единичной функцией

[1]d

)δ(

= . (1.24)

Из этого следует аналогичная связь между переходной и импульсной

характеристиками линейных звеньев:

(t) h

(t) w

= , (1.25)

и наоборот:

ttwth

d()(

∫

= )

. (1.26)

1.2.5. Частотные характеристики

Частотные характеристики широко используются при анализе и син-

тезе систем автоматического регулирования. Понятие «частотные характе-

ристики» применимо как к отдельным звеньям, так и к системе автомати-

ческого регулирования в целом.

В основу выявления частотных характеристик положена реакция зве-

на и системы на гармонический входной сигнал. Если на вход линейной

системы подать

гармонический входной сигнал, то по истечении некоторо-

го времени после подачи такого входного сигнала, в интервале которого

затухает свободная составляющая выходного сигнала, т. е. после того как

закончится переходный процесс, выходной сигнал также будет гармониче-

ским с той же частотой, которую имеет входной сигнал, но с иными ам-

плитудой и

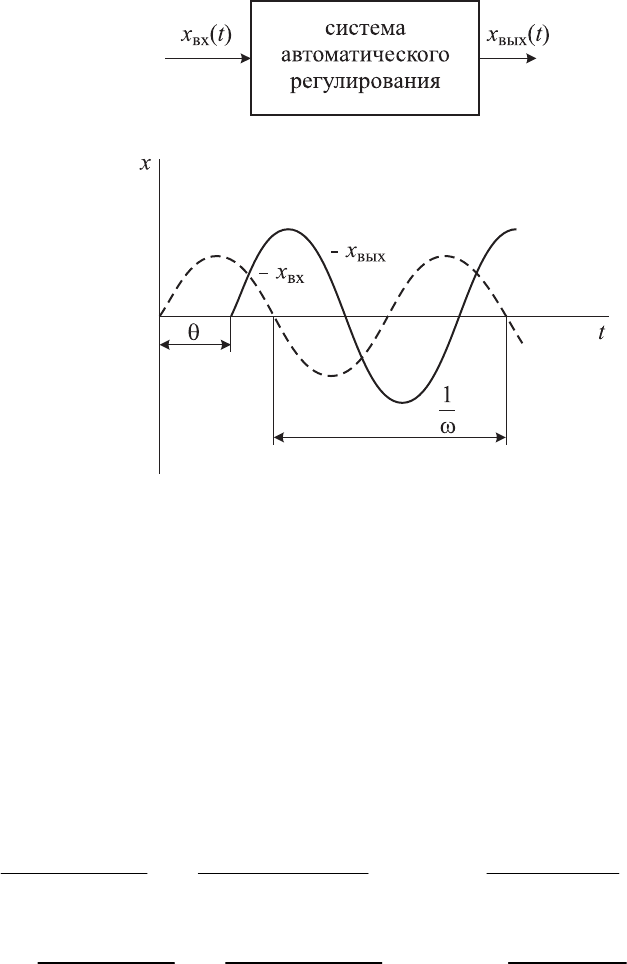
фазой (рис. 1.6). Амплитуда и фаза выходного сигнала будут

зависеть от частоты, и по ним можно судить о динамических свойствах как

звеньев, так и системы в целом.

Гармонический входной сигнал в символической форме описывается

следующим выражением:

хtх

вх.мвх

е)( = , (1.27)

где ω — частота гармонического сигнала.

Учитывая, что

tj t

ωsin ω cosе

+= , (1.28)

то это выражение представляет собой единичный вектор, у которого

cos ωt и sin ωt представляют собой вещественную и мнимую составляющие

этого вектора.

Рис. 1.6. Графики изменения выходного

и входного сигналов в установившемся режиме

В установившемся режиме вынужденные периодические колебания

(см. рис. 1.6) определяются следующим выражением:

θω

вых.м

θ) (ω

вых.мвых

ее)(

jtjj

еххtх ==

. (1.29)

Пусть в общем случае система автоматического регулирования опи-

сывается следующим дифференциальным уравнением:

(

)

(

)

(

)

()

() () ()

()

вых вых вых

01 1

вх вх вх

01 1 вх

вых

...

... .

−

⎡⎤ ⎡⎤ ⎡⎤

⎣⎦ ⎣⎦ ⎣⎦

++++=

⎡⎤ ⎡⎤ ⎡⎤

⎣⎦ ⎣⎦ ⎣⎦

=+ ++ +

dx t d x t dx t

cc c cxt

dt dt

dxt d xt dxt

bb b bxt

dt dt

(1.30)

Принимая входной сигнал гармоническим и зная, что

⎪

⎭

⎪

⎬

⎫

,eω)()e(

,eω)e(

ω ω

tjtj

хjх

LLLLLLLLLLL

(1.31)

уравнение (1.30), с учетом (1.27) и (1.29), запишем в следующем виде:

.еω)(ω)(ω)(

e еω)(ω)(ω)(

вх.м

θω

вых.м

j j

х bjb...jbjb

х cjc...jcjc

⎥

⎦

⎤

⎢

⎣

⎡

++++=

⎥

⎦

⎤

⎢

⎣

⎡

++++

−

(1.32)

Сокращая в этом уравнении е

jωt

, получим выражение, определяющее

зависимость соотношения амплитуд и фазы выходного сигнала от частоты:

ω)(

ω)(ω)(ω)(

еω)(

вх.м

вых.м

jМ

jЕ

cjc...jcjc

bjb...jbjb

++++

−

. (1.33)

Полученная функция W(jω) называется комплексной частотной харак-

теристикой.

Из сравнения (1.15) и (1.33) следует, что комплексная частотная ха-

рактеристика может быть получена по передаточной функции путем под-

становки в нее р = jω.

Комплексную частотную характеристику можно представить в декар-

товых координатах на комплексной плоскости как геометрическую сумму

ее вещественной R

(ω) и мнимой I(ω) составляющих:

)(ω)(ωω)( j

, (1.34)

или в полярных координатах в показательной форме вектора с модулем

А(ω) и фазой θ(ω):

) (ω θ

e ) (ωω)(

АjW = . (1.35)

В этом выражении

) (ω) (ωω)() (ω

IRjWА +== ; (1.36)

()

) (ω

arctgωθ

. (1.37)

Если представить W(jω) как вектор, который характеризует устано-

вившийся процесс при периодическом входном сигнале с частотой ω,

и изменяя частоту в пределах 0 ≤ ω ≤ ∞, то конец этого вектора прочертит

на комплексной плоскости кривую, называемую годографом вектора ком-

плексной частотной характеристики. Эта же кривая в координатах [R(ω

I(ω) ] называется амплитудно-фазовой частотной характеристикой

(АФЧХ). Примеры таких характеристик приведены на рис. 1.7. При изме-

нении частоты в указанных пределах, т. е. от 0 до ∞, вектор будет вращать-

ся либо против часовой стрелки, либо по часовой стрелке. При этом угол

поворота будет положительным при вращении вектора против часовой

стрелки

(см. рис. 1.7, а) и отрицательным при вращении вектора по часо-

вой стрелке (см. рис. 1.7, б).

Зависимости вещественной и мнимой составляющей комплексной

частотной характеристик R(ω) и I(ω) соответственно называются вещест-

венной частотной характеристикой и мнимой частотной характеристикой.

Зависимость А(ω), характеризующая соотношение амплитуд выходного

и входного сигналов, при изменении

ω называется амплитудно-частотной

характеристикой (АЧХ), а зависимость θ(ω) характеризующая его фазу,

при изменении ω, называется фазочастотной

характеристикой (ФЧХ).

Широкое применение в практике расчета и проектирования систем

автоматического регулирования находят амплитудно-частотная и фазоча-

стотная характеристики, построенные в логарифмическом масштабе, назы-

ваются логарифмическими частотными характеристиками.

Если комплексную частотную характеристику (1.35) прологарифми-

ровать, то можно записать

θ(ω)) (ωln)e (ωlnω)(ln

θ(ω)

jА А jW

+== . (1.38)

Характеристика ln A(ω), построенная в логарифмическом масштабе по

оси абсцисс и в обычном линейном масштабе по оси ординат, называется

логарифмической амплитудной частотной характеристикой

(ЛАЧХ). Ха-

рактеристика θ(ω), построенная в логарифмическом масштабе по оси абс-

цисс и в линейном масштабе по оси ординат называется логарифмической

фазовой частотной характеристикой (ЛФЧХ).