Динкель А.Д. Теория автоматического управления
Подождите немного. Документ загружается.

33
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−
−
−=
−−
21
ee
12
2
21
1
вых
1)(
T
t
T
t
TT
T
TT
T
Ktх , (2.27)
оно описывает переходную характеристику (см. рис. 2.3, а).
Исходя из (2.26), передаточная функция звена
1)1)(()(
)(
)(
21вх
вых
++
==
рТрТ
K
pХ
pX
pW
. (2.28)
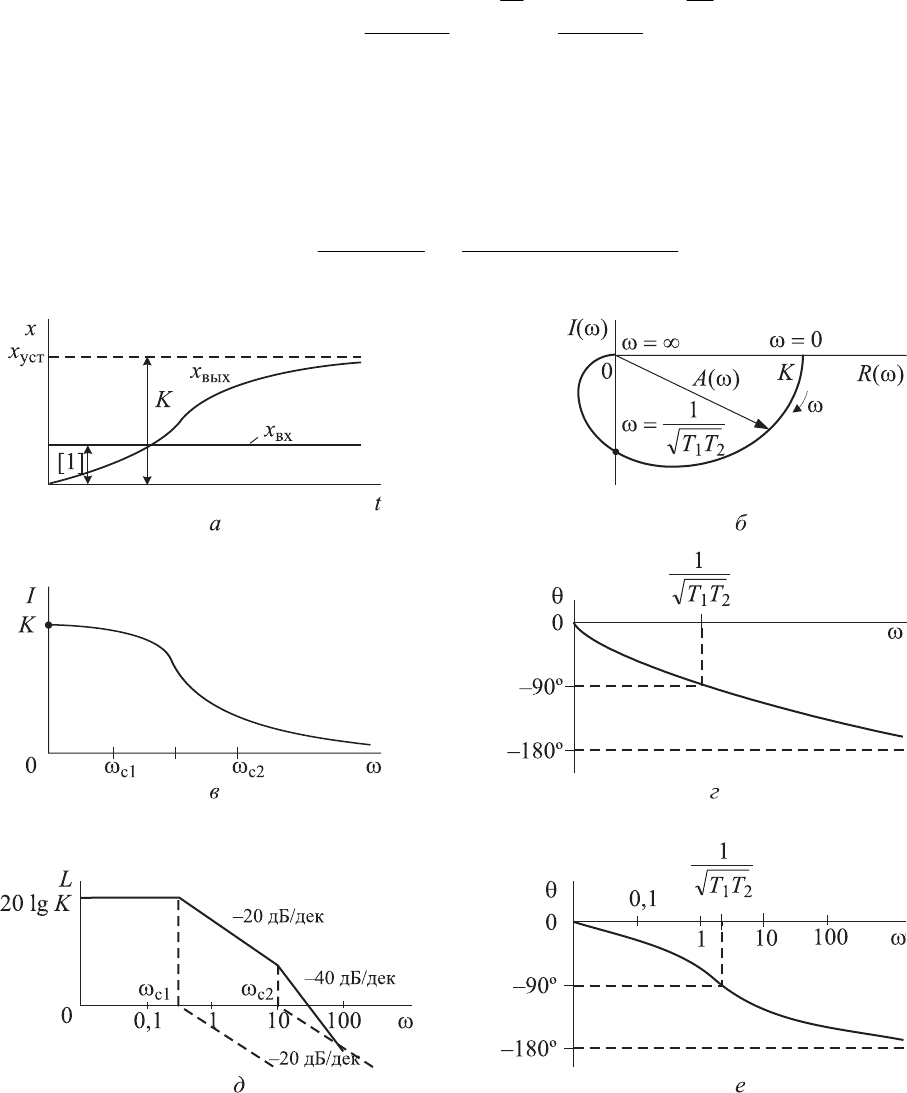
Рис. 2.3. Характеристики инерционного звена второго порядка:
а — переходная; б — амплитудно-фазовая частотная; в — амплитудно-
частотная; г — фазочастотная; д — логарифмическая амплитудно-частотная;
е — логарифмическая фазочастотная
На основании этой передаточной функции получим комплексную час-
тотную характеристику:
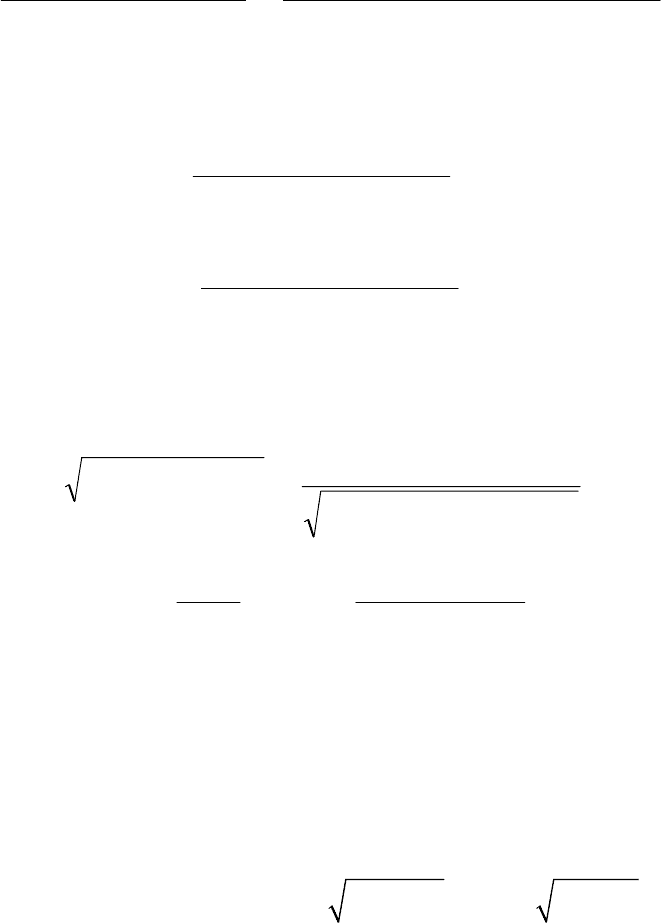
34
1)ω1)(ω(
] )ω(1)ω[(
1)ω1)(ω(
ω)(
22
2
22
1
21
2
21
21
++
+−+−
=
++
=
TT
TTjTTK
jТjТ
K
jW
,(2.29)
и соответственно вещественную и мнимую частотные характеристики:
=
) (ωR
1)ω1)(ω(
1)ω(
22
2
22
1
2
21
++
+−
TT
TTK
; (2.30)
=
) (ω
I
1)ω1)(ω(
)ω(
22
2
22
1
21
++
+
−
TT
TTK
. (2.31)
Тогда, исходя из (2.30) и (2.31), амплитудно-частотную и фазочастот-
ную характеристики запишем в следующем виде:
1)ω1)(ω(
) (ω) (ω) (ω
22
2
22
1
22
++
=+=
ТT
K
IRА ; (2.32)
1)ω(
ω )(
arctg
) (ω
) (ω
arctg) θ(ω
2
21
21
+−
+
−==
ТТ
ТT
R
I
. (2.33)
Графики этих характеристик приведены на рис. 2.3, в и г.
Годограф вектора )ω(
А
, который является амплитудно-фазовой час-
тотной характеристикой, приведен на рис. 2.3, б.
Логарифмируя (2.32), получим выражение для логарифмической ам-
плитудной частотной характеристики
22 2
12
( ) 20 lg ( ) 20 lg 20 lg 1 20 lg 1ω= ω= − ω+− ω+LAKT T. (2.34)
Анализируя полученное выражение, можно заключить, что логариф-
мическая амплитудно-частотная характеристика, по сути своей, является
алгебраической суммой логарифмических амплитудных частотных харак-
теристик безынерционного звена и двух инерционных звеньев первого по-
рядка (рис. 2.3, д).
Из (2.33) следует, что

35
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎬
⎫
∞==
==
==
.ωпри–180θ(ω)
;
1
ωпри–90θ(ω)
0;ωпри0θ(ω)
21
o
o
ТТ
(2.35)
График логарифмической фазовой частотной характеристики приве-
ден на рис. 2.3, е.
Для уточнения логарифмических амплитудно-частотных характери-
стик в окрестности частот сопряжения ω
с1
и ω
с2
можно воспользоваться
таблицей поправок (см. табл. 2.1).
2.4. Колебательное звено
Звено называется колебательным, если связь между выходным и вход-
ным сигналами описывается линейным дифференциальным уравнением
)()(
d
)](d[
2ξ
d
)]([d
вхвых
вых
2
вых
2
2
tх Ktх
t
tх
Т
t
t
Т =++
х
, (2.36)
при условии
044ξ
222
<− ТТ или 01ξ
2
<− , (2.37)
следовательно 1ξ0 << ,
где Т — постоянная времени;
K — передаточный коэффициент;
ξ — коэффициент демпфирования (постоянная затухания).
Запишем уравнение (2.36) в операторной форме:
)()(1)2ξ(
вхвых
22
рKXрX ТррТ =++
. (2.38)
Приравняв левую часть этого уравнения нулю, получим характери-
стическое уравнение
01ξ2
22
=++ ТррТ , (2.39)
корни которого

36
Т
Т
ТТТ
р
1ξξ
2
44ξ 2ξ
2
2
222
1,2
−±−
=
−±−
= . (2.40)
В связи с тем, что значения ξ находятся в пределах 0 < ξ < 1, эти кор-
ни будут комплексно-сопряженными. Введя обозначения
Т
ξ
α =
,
Т
2
ξ1
β
−
=
,
получим выражение для корней в следующем виде:
βα
1,2
j±−=р . (2.41)
Запишем решение исходного уравнения при входном сигнале в виде
единичной ступенчатой функции, с учетом принятых обозначений:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ϕ+−= ) (βsin
β
1
1)(
α
вых
e t
t
t
Ktх
, (2.42)
где
α
β
arctg=ϕ
— начальная фаза выходного сигнала, это выражение
представляет собой аналитическое описание переходной характеристики,
которая приведена на рис. 2.4,
а.
Переходная характеристика оценивается по следующим параметрам:
ξ — коэффициент демпфирования;
1
21
ψ
А
АА −
=
— степень затухания;
α
β
µ =
— степень колебательности.
Исходя из (2.38) передаточная функция колебательного звена
12ξ
)(
)(
)(
22
вх
вых
++
==
ТррТ
K
pХ
pX
pW
, (2.43)
в соответствии с ней получим комплексную частотную характеристику
в следующем виде:
222222
22
22
ω4ξ)ω(1
ω]2ξ)ω[(1
1 ω2ξω
ω)(
TT
TjT K
ТjТ
K
j W
+−
−−
=
++−
=
, (2.44)
37
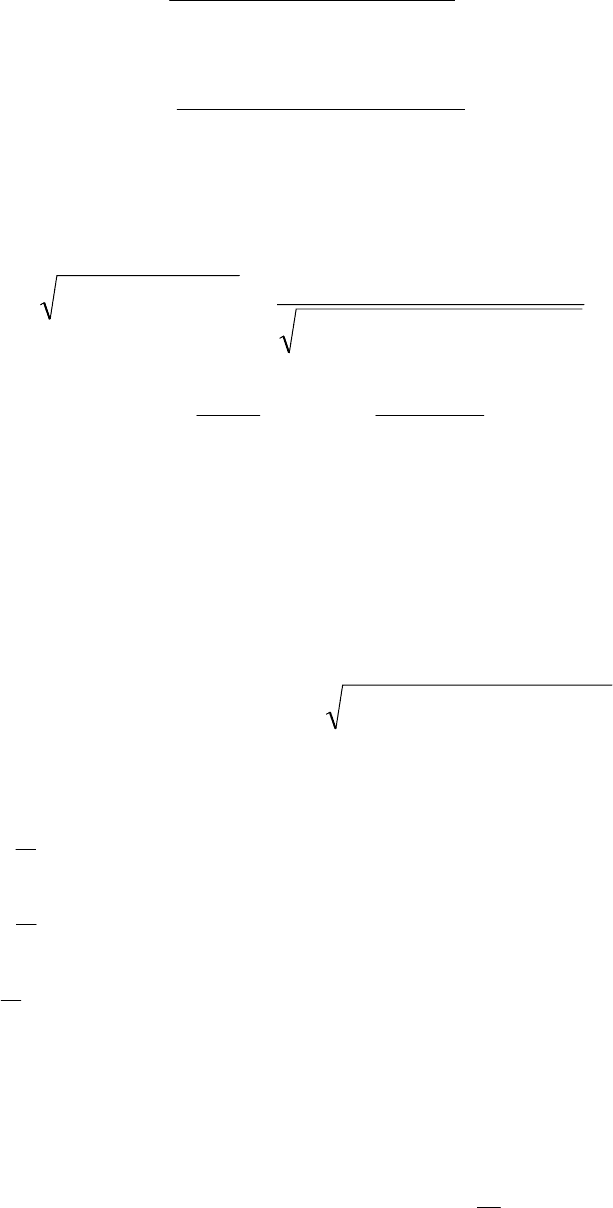
в соответствии с которой вещественная частотная характеристика:
222222
22
ωT4ξ)ω(1
)ω(1
) (ω
+−
−
=
T
TK
R
, (2.45)
22222
ω4ξ)ω1
ω ξ2
) (ω
T
2
T(
I
+−
−=
TK
. (2.46)
Тогда в соответствии с (2.45) и (2.46) амплитудно-частотная и фазо-
частотная характеристики запишутся в следующем виде:
222222
22
ω4ξ)ω(1
) (ω) (ω) (ω
ТT
K
IRА
+−
=+= ; (2.47)
22
ω1
ω2ξ
arctg
) (ω
) (ω
arctg) θ(ω
Т
R
I
−
−==
Т
; (2.48)
их графики приведены на рис. 2.4,
в и г.
Годограф вектора )ω(
А
, являющийся амплитудно-фазовой частотной
характеристикой, приведен на рис. 2.4,
б.
Логарифмируя (2.47), получим логарифмическую амплитудную час-
тотную характеристику
22222
ω4ξ)ω(1lg 20lg 20) (ωlg 20) ω ТT +−−== KAL( . (2.49)
Исходя из этого выражения получим, что
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎬
⎫
==
=≈>>
≈<<
. 2ξ lg 02–lg20) (ω
1
ωпри
;ω40lg20ω lg 02–lg20) (ω
1
ωпри
;lg20) (ω
1
ωпри
22
KL
Т
– KKL
Т
KL
Т
TT (2.50)
Если принять ξ = 1, то логарифмическую амплитудную частотную ха-
рактеристику, согласно (2.50), приближенно можно представить двумя
прямыми, первая из которых параллельна оси ординат и удалена от нее на
K
lg20 , а вторая, сопрягающаяся с первой при
Т
1
ω
с
=
, имеет наклон по
38
отношению к оси абсцисс — 40 дБ/дек, как это показано на рис. 2.4, д. При
значении 0ξ = и
Т
1
ω
с
=
эта характеристика уходит в бесконечность, а
характер ее изменения в окрестности ω
с
будет зависеть от промежуточных
значений
ξ (см. рис. 2.4, д).
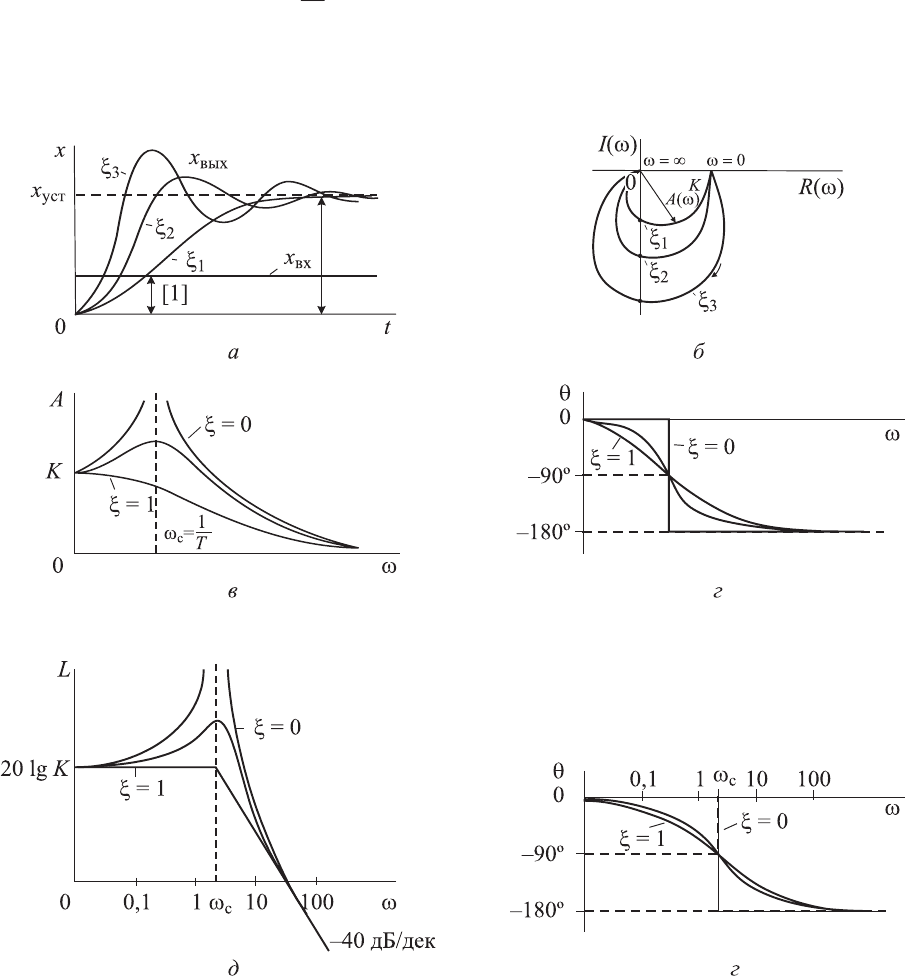
Рис. 2.4. Характеристики инерционного колебательного звена второго по-
рядка:
а — переходная; б — амплитудно-фазовая частотная;
в — амплитудно-частотная; г — фазочастотная; д — логарифмическая ам-
плитудно-частотная;
е — логарифмическая фазочастотная
Логарифмическая фазовая частотная характеристика колебательного
звена также зависит от
ξ (2.48) и характер ее изменения в зависимости от
значений
ξ будет аналогичен характеру изменения амплитудно-частотной
характеристики.
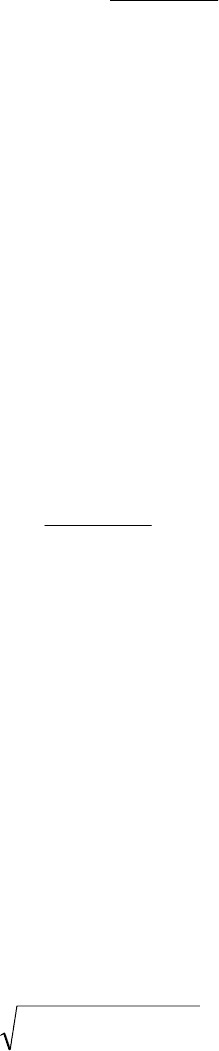
39
2.5. Дифференцирующее звено первого порядка
Дифференцирующее звено может быть идеальным или реальным.
Звено называется идеальным, если связь между выходным и входным
сигналами описывается уравнением
t
tх
Ktх
d
)]([ d
)(
вх
вых
= , (2.51)
где K — передаточный коэффициент звена.
Следовательно, в таком звене выходной сигнал пропорционален ско-
рости изменения входного сигнала.
Решение этого уравнения, при входном сигнале в виде единичной
ступенчатой функции [1])(
вх
=tх , представляет собой дельта-функцию и
является аналитическим описанием переходной характеристики идеально-
го дифференцирующего звена.
)δ()(
вых
t Ktх
=
. (2.52)
График этой характеристики приведен на рис. 2.5, а.
Исходя из (2.50), передаточная функция
Kp
pХ
pX
W(p) ==
)(
)(
вх
вых
. (2.53)
Соответственно комплексная частотная характеристика запишется в
следующем виде:
ω)ω( K
j
j
W
=
, (2.54)
откуда вещественная частотная характеристика
0)(ω
=
R
; (2.55)
ω)(ω
K
I
=
. (2.56)
Тогда амплитудно-частотную и фазочастотную характеристику можно
записать в виде
ω) (ω) (ω) (ω
22
KIRА =+= ; (2.57)
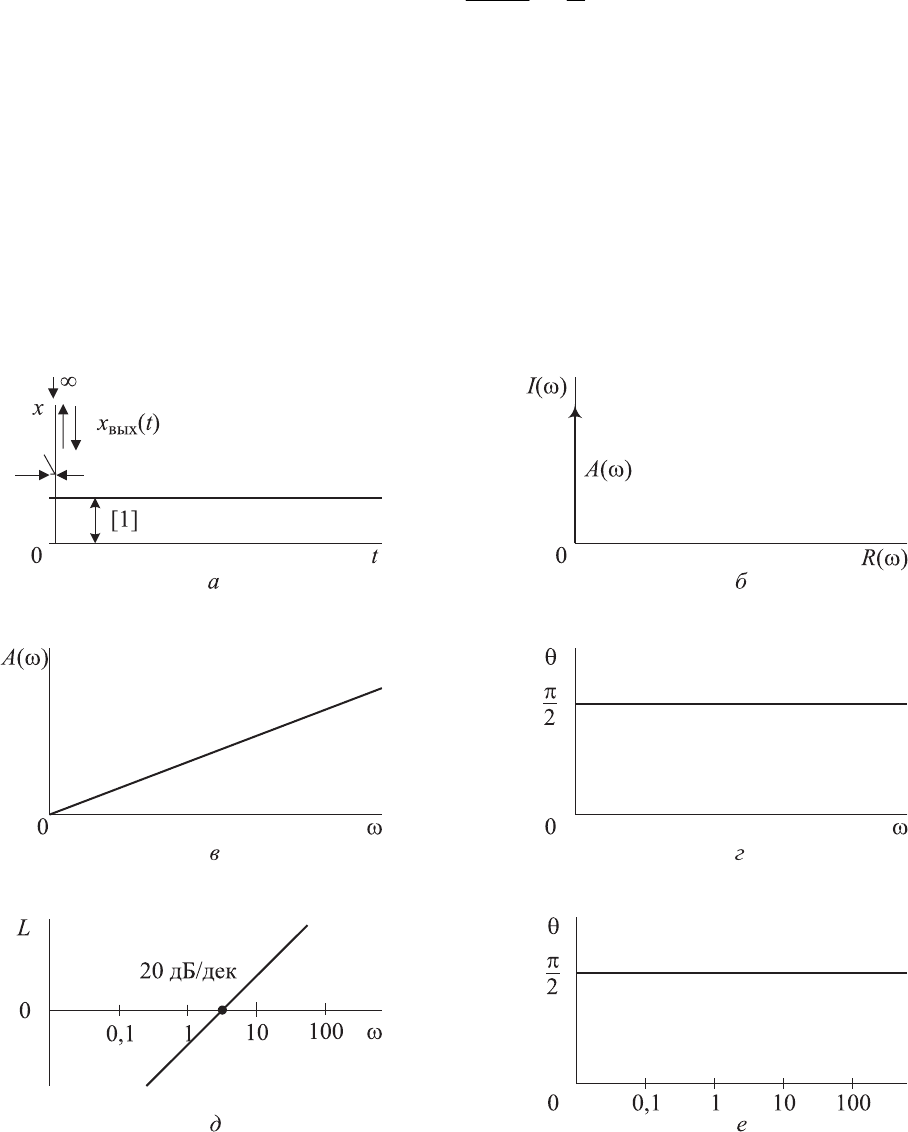
40
2
π
) (ω
) (ω
arctg) θ(ω
==
R
I
, (2.58)
их графики приведены на рис. 2.5, в и г.
Годограф вектора )ω(
А
, являющийся амплитудно-фазовой частотной
характеристикой, приведен на рис. 2.5, б.
Логарифмируя (2.57), получим аналитическое описание логарифмиче-
ской амплитудной частотной характеристики:
ωlg20)(ωlg20) (ω
K
A
=
=
L
. (2.59)
График этой характеристики приведен на рис. 2.5, д.
Рис. 2.5. Характеристики идеального дифференцирующего звена:
а — переходная; б — амплитудно-фазовая частотная; в — амплитудно-
частотная;
г — фазочастотная; д — логарифмическая амплитудно-частотная;
е — логарифмическая фазочастотная

41
Как следует из (2.58), логарифмическая фазовая частотная характери-
стика представляет собой прямую, параллельную оси абсцисс и удаленную
от нее на
2
π
(рис. 2.5, е).
В практике используются так называемые реальные дифференцирую-
щие звенья, выполняющие приближенное дифференцирование с опреде-
ленной точностью. Такие звенья называются реальными дифференцирую-
щими звеньям, и связь между выходным и входным сигналами описывает-
ся следующим уравнением:
()
[
]
()
(
)
[
]
t
tх
Ktх
t
tx
T
d
d
d
d
вх
вых
вых
=+
, (2.60)
где
Т — постоянная времени звена.
Решение этого уравнения, при входном сигнале в виде единичной
ступенчатой функции
х
вх
(t) = [1], определяется следующей зависимостью:
T
t
Ktх
−
= е)(
вых
, (2.61)
которая представляет собой переходную характеристику звена. График
переходной функции реального дифференцирующего звена приведен на
рис. 2.6,
а.
Уравнение (2.60) в операторной форме запишется в следующем виде:
)()(1)(
вхвых
рKрХрХТр
=
+ . (2.62)
Тогда передаточная функция
1)(
)(
)(
вх
вых
+
==
Tp
Kp
pX
pX
pW
, (2.63)
и в соответствии с этой передаточной функцией комплексная частотная
характеристика
1ω
)ω( ω
1ω
ω
) ω(
22
+
+
=
+
=
T
jTK
Тj
Kj
jW
. (2.64)
Тогда получим
42
1ω
ω
) (ω
22
22
+
=
T
KT
R
; (2.65)
1ω
ω
) (ω
22
+
=
T
K
I
, (2.66)
а амплитудная и фазовая частотные характеристики будут следующими:
1ω
ω
) (ω) (ω) (ω
22
22
+
=+=
Т
K
IRА
; (2.67)
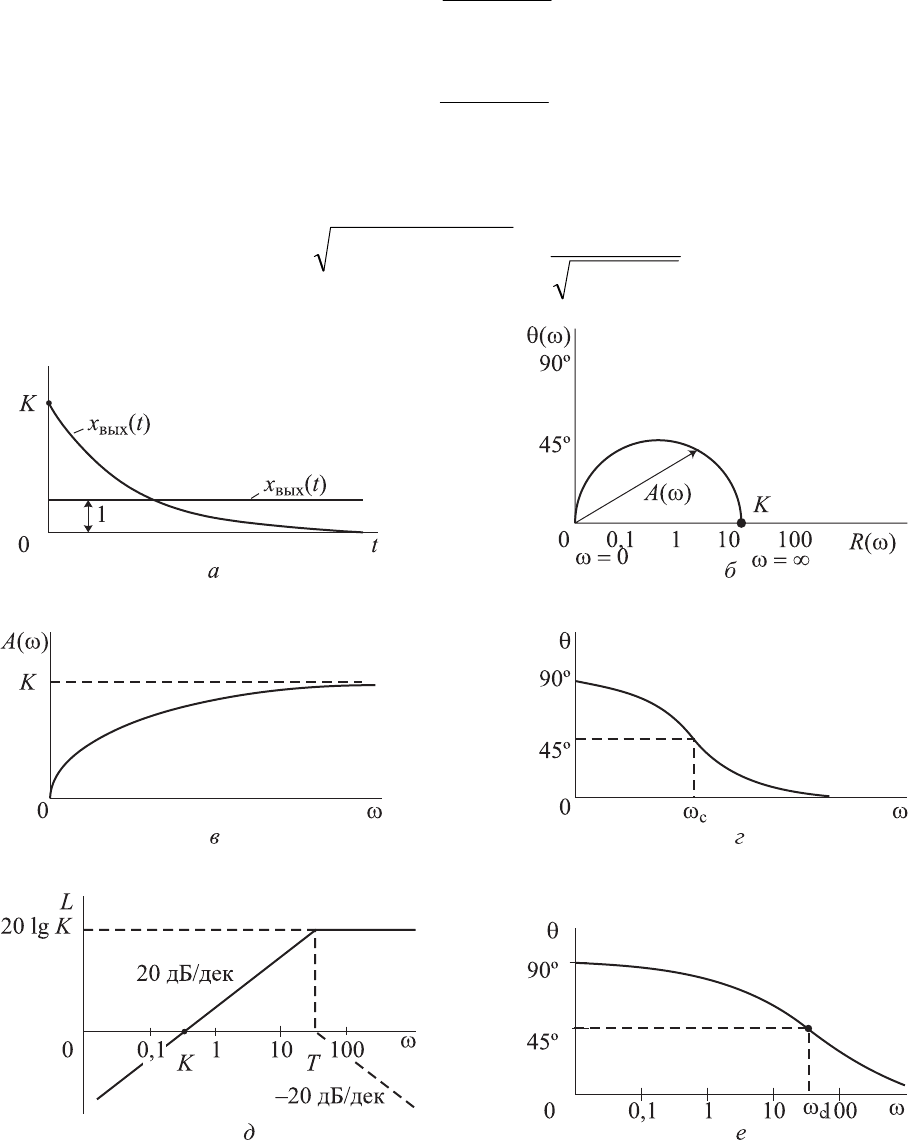
Рис. 2.6. Характеристики реального дифференцирующего звена:
а — переходная; б — амплитудно-фазовая частотная; в — амплитудно-
частотная;
г — фазочастотная; д — логарифмическая амплитудно-частотная;
е — логарифмическая фазочастотная
