Динкель А.Д. Теория автоматического управления
Подождите немного. Документ загружается.


43
ω arctg90
ω
1
arctg
) (ω
) (ω
arctg) θ(ω
о
T
T
−===
R
I
. (2.68)
Графики этих характеристик приведены на рис. 2.6,
в, г.
Амплитудно-фазовая частотная характеристика, являющаяся годогра-
фом вектора ) (ω
А
, приведена на рис. 2.6, б.
В результате логарифмирования (2.67) получим логарифмическую
амплитудную частотную характеристику в следующем виде:
() ()
22
ω 20 lg ω 20 lg ωω1LA KT== +. (2.69)
Из этого выражения следует, что логарифмическая амплитудно-
частотная характеристика реального дифференцирующего звена
(см. рис. 2.6,
д), представляет собой алгебраическую сумму двух состав-
ляющих, первая из которых является характеристикой идеального диф-
ференцирующего звена, а вторая — апериодического звена первого
порядка, т. е. она состоит из двух прямых, сопрягающихся при частоте
Т
1
ω
с
=
, как это показано на рис. 2.6, д.
Согласно (2.68) логарифмическая фазовая частотная характеристика
θ(ω) = 90° при ω = 0,
θ(ω) = 45° при ω = ω
с
,
θ(ω) = 0 при ω = ∞.
График этой характеристики приведен на рис. 2.6,
е.
2.6. Дифференцирующее звено второго порядка
Звено называется дифференцирующим второго порядка, если динами-
ческие процессы описываются следующим линейным дифференциальным
уравнением второго порядка:
[]
[
]
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
++=
)(
d
)( d
2ξ
d
)(d
)(
вх
вх
2
вх
2
2
вых
tх
t
tх
T
t
tх
TKtх
, (2.70)
где
K — передаточный коэффициент;
Т — постоянная времени,
или в операторной форме

44
)(1) 2ξ()(
вх
22
вых
рХТррТKрX ++=
. (2.71)
Решение этого уравнения, представляющее собой переходную харак-
теристику, при [1])(
вх
=tх имеет следующий вид:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
++=
1)δ( 2ξ
d
)]( [δ d
)(
2
2
вых
tТ
t
ТKt
t
х . (2.72)
График этой характеристики приведен на рис. 2.7,
а.
Передаточная функция, согласно (2.69) равна
1) 2ξ(
)(
)(
22
вх
вых
++== ТpрТK
pХ
pX
W(p)
. (2.73)
Тогда комплексная частотная характеристика
1) 2ξω() ω(
22
++−= ТjТKWj , (2.74)
исходя из нее, получим вещественную и мнимую частотные характеристи-
ки:
)ω(1) (ω
22
ТKR −=
; (2.75)
ωξ2)(ω
Т
K
I
=
. (2.76)
Амплитудно-частотная и фазочастотная характеристики, с учетом
(2.75) и (2.76), соответственно запишем в виде
22222222
ω4ξ)ω(1) (ω) (ω) (ω ТТKIRА +−=+= ; (2.77)
22
ω1
ω 2ξ
arctg
) (ω
) (ω
arctgθ(ω)
T
Т
−
==
R
I
. (2.78)
Графики этих характеристик приведены на рис. 2.7,
в, г.
Амплитудно-фазовая частотная характеристика, являющаяся годогра-
фом вектора
А(ω) на комплексной плоскости, показана на рис. 2.7, б.
Логарифмическая амплитудная частотная характеристика, полученная
в результате логарифмирования (2.77), определяется следующим выражением:
22222
ω4ξ)ω(1lg 20 lg 20(ωω lg 20) (ω ТTKAL +−+==
. (2.79)
45
Из анализа этого выражения следует, что при
ξ = 1 логарифмическая
амплитудная частотная характеристика в логарифмическом масштабе со-
стоит из двух прямых, одна из которых при
Т
1
ω
= параллельна оси абсцисс
и удалена от нее на 20 lg
K, а вторая — наклонная с наклоном 40 дБ/дек
при
Т
1
ω
= и сопрягающаяся с первой при
Т
1
ω
с
= . При 0
=
ξ
и
Т
1
ω
= эта
характеристика стремится к минус бесконечности. Графики рассматривае-
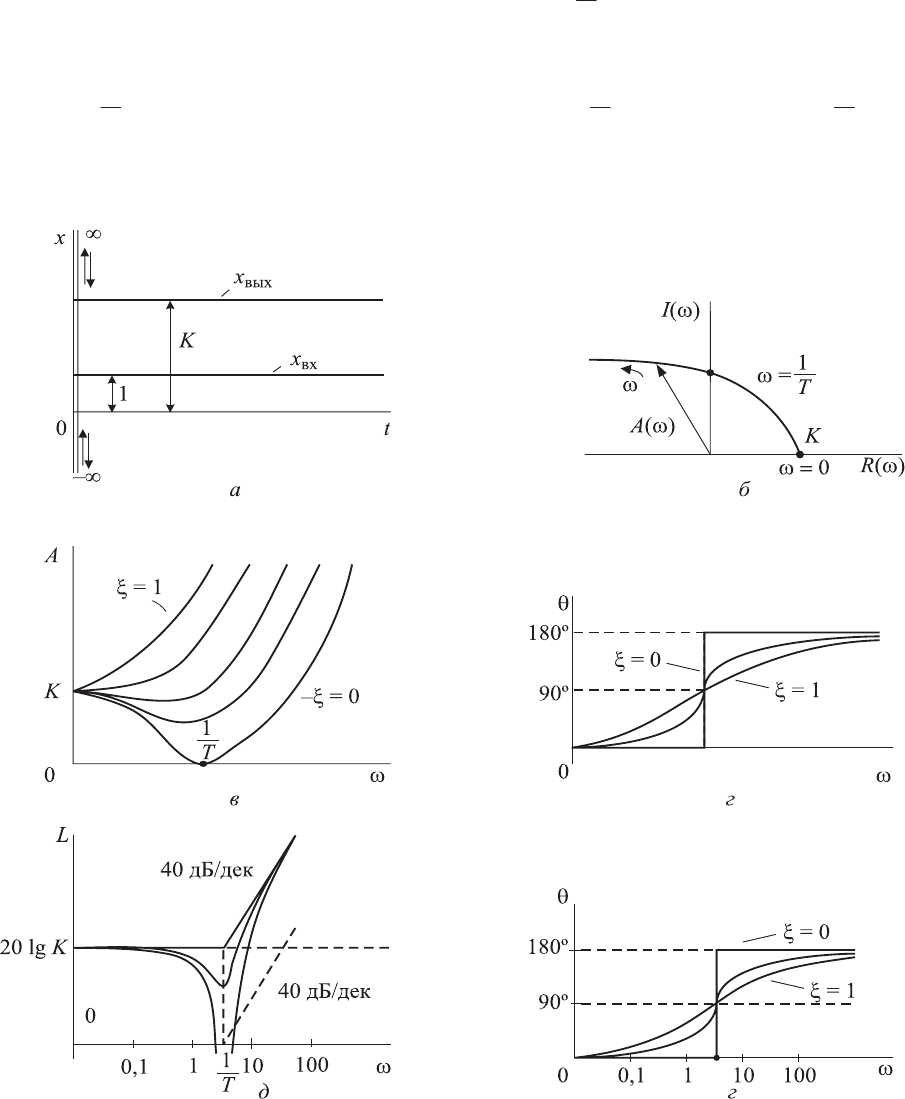
мой характеристики приведены на рис. 2.7,
д.
Рис. 2.7. Характеристики дифференцирующего звена второго порядка:
а — переходная; б — амплитудно-фазовая частотная; в — амплитудно-
частотная;
г — фазочастотная; д — логарифмическая амплитудно-частотная;
е — логарифмическая фазочастотная

46
Из анализа (2.76) следует, что при
ξ = 1 логарифмическая фазовая час-
тотная характеристика плавно изменяется от 0 до 180
о
, проходя через точ-
ку с координатами (1/
Т, 90
о
). При ξ = 0 эта характеристика скачком изме-
няется от 0 до 180
о
на частоте ω
с
. Графики логарифмических фазовых час-
тотных характеристик приведены на рис. 2.7,
г.
2.7. Интегрирующее звено
Интегрирующим называется звено, у которого выходной сигнал про-
порционален интегралу по времени от входного сигнала
() ()
∫
= ttx
T
x d
1
выхвых
t . (2.80)
При входном сигнале, представляющем собой одиночную ступенча-
тую функцию, выполняя интегрирование (2.80) получим уравнение, опре-
деляющее характер переходной характеристики:
()
tt
T
x
1
вых
=
. (2.81)
График переходной характеристики приведен на рис. 2.8,
а.
Запишем уравнение (2.80) в операторной форме:
)(
1
)(
вхвых
рХ
Тр
рХ =
, (2.82)
согласно ему передаточная функция
ТррХ
рХ
W(р)
1
)(
)(
вх
вых
==
.
Исходя из передаточной функции, запишем комплексную частотную
характеристику:
ω
1
) ω(
Т
jjW −=
. (2.83)
Следовательно вещественная и мнимая частотные характеристики равны:
0)(ω
=
R
; (2.84)
ω
1
) (ω
Т
I −=
, (2.85)
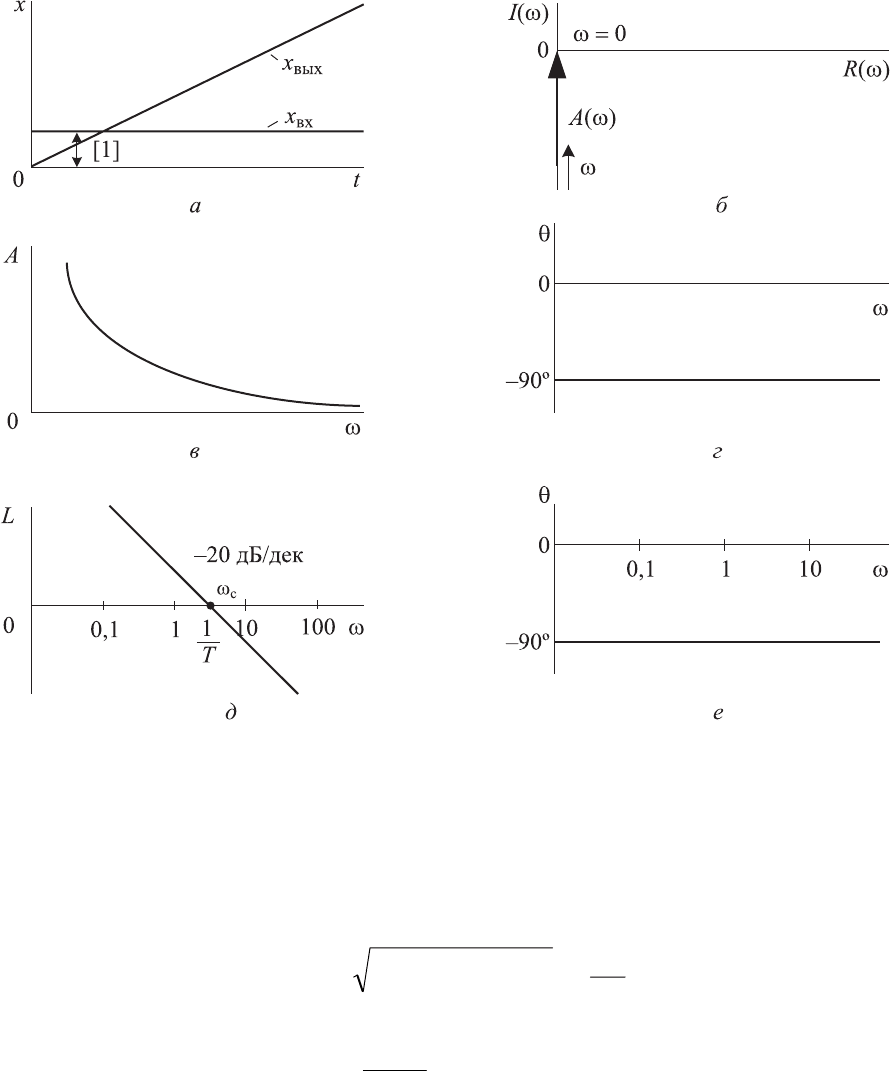
47
Рис. 2.8. Характеристики интегрирующего звена:
а — переходная;
б — амплитудно-фазовая частотная; в — амплитудно-частотная;
г — фазочастотная; д — логарифмическая амплитудно-частотная;
е — логарифмическая фазочастотная
соответственно амплитудно-частотная и фазочастотная характеристика
ω
1
) (ω) (ω) (ω
22
T
=+= IRА
; (2.86)
o
90)( arctg
) (ω
) (ω
arctg) θ(ω −=−∞==
R
I
. (2.87)
Графики этих характеристик приведены на рис. 2.8,
в, г.
Амплитудно-фазовая частотная характеристика, являющаяся годогра-
фом вектора
А(ω) приведена на рис. 2.8, б, из которой видно, что эта ха-
рактеристика совпадает с отрицательной частью оси ординат.

48
Логарифмическая амплитудная частотная характеристика, получае-
мая в результате логарифмирования (2.86), определяется следующим вы-
ражением:
ω
1
lg 20) (ω lg 20) (ω
T
== AL
. (2.88)
Из этого выражения следует, что
⎪
⎪
⎭
⎪
⎪
⎬
⎫
==
==
==
.
10
ωпридБ/дек20) (ω
;
0,1
ωпридБ/дек20) (ω
;
1
ωпри0) (ω
Т
Т
Т
L
L
L
(2.89)
Согласно этому логарифмическая амплитудная частотная характери-
стика представляет собой прямую проходящую под наклоном –20 дБ/дек
и пересекающую ось абсцисс при значении
Т
1
ω
с
= , как это показано на
рис. 2.8, д. Логарифмическая фазовая частотная характеристика, как это
следует из (2.87), не зависит от частоты и представляет собой прямую,
параллельную оси абсцисс и удаленную от нее на величину
о
90θ(ω) −=
(см. рис. 2.8, г).
2.8. Запаздывающее звено
Звено является запаздывающим, если его динамические свойства, т. е.
зависимость между выходным и входным сигналами, описывается сле-
дующим дифференциальным уравнением:
τ)()(
вхвых
−
=
tKхtх , (2.90)
где K — передаточный коэффициент;
τ — время запаздывания.
По (2.90) можно заметить, что при t > τ выходной сигнал равен нулю,
а при
τ≥
t
этот сигнал повторяет входной сигнал, отставая от него по вре-
мени на величину τ (рис. 2.8, а).
В операторной форме это уравнение запишется в виде

49
)()(
вх
τ
вых
е рX KрХ
р−
= . (2.91)
Переходная характеристика запаздывающего звена приведена на
рис. 2.8, а.
Следовательно, передаточная функция запаздывающего звена
τ
вх
вых
е
)(
)(
р
K
рХ
рХ
рW
−
==)( , (2.92)
а комплексная частотная характеристика запишется в следующем виде:
ωτ
е) ω(
j
KW
−
=j , (2.93)
или в тригонометрической форме
ωτ)sin ωτ (cos) ω(
jj
−
=
K
W . (2.94)
Исходя из (2.94), вещественная и частотная характеристики
ωτcos)(ω
K
R
=
; (2.95)
мнимая характеристика
ωτsin )(ω
K
I
−
=
. (2.96)
Тогда амплитудно-частотная и фазочастотная характеристики запи-
шутся в следующем виде:
KKIRА =+=+= ωτsinωτcos) (ω) (ω) (ω
2222
; (2.97)
ωτ
) (ω
) (ω
arctgθ(ω) −==
R
I
, (2.98)
графики их приведены на рис. 2.8,
в, г.
Амплитудно-фазовая частотная характеристика, являющаяся годогра-
фом вектора
А(ω), который он опишет на комплексной плоскости при еди-
ничном ступенчатом входном сигнале [1])(
вх
=
tх , и, как это следует из
(2.106) представляет собой окружность с радиусом
K (см. рис. 2.8, б).
Из (2.97) следует, что логарифмическая амплитудная частотная харак-
теристика запаздывающего звена
K
A
L
lg20)(ωlg20) (ω
=
= , (2.99)
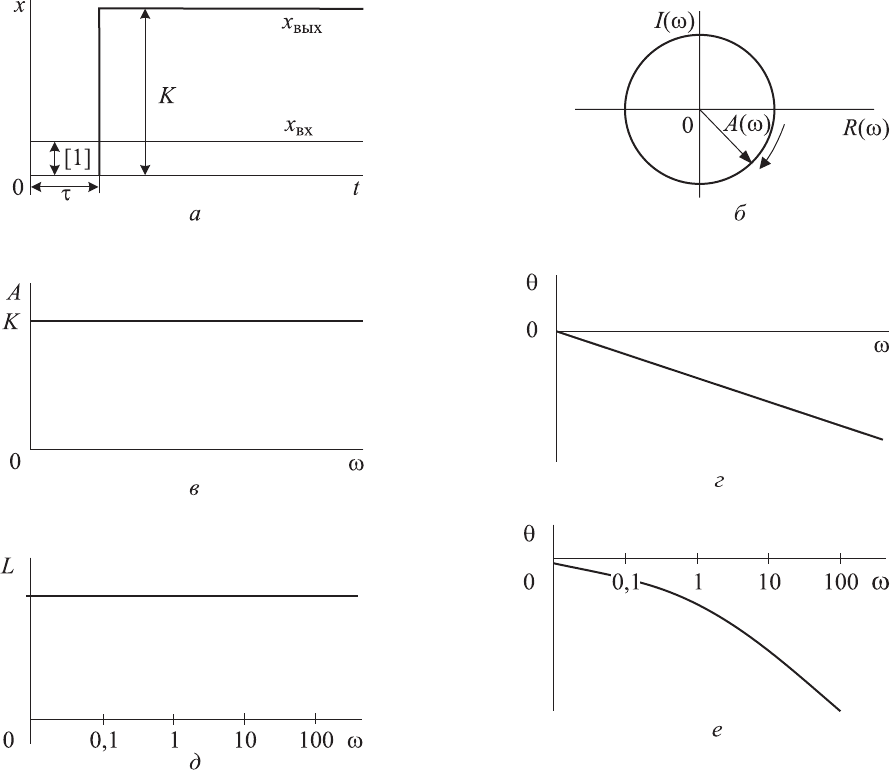
50
Рис. 2.9. Характеристики запаздывающего звена:
а — переходная;
б — амплитудно-фазовая частотная; в — амплитудно-частотная;
г — фазочастотная; д — логарифмическая амплитудно-частотная;
е — логарифмическая фазочастотная
а ее график представляет собой прямую, параллельную оси абсцисс и уда-
ленную от нее на
K
lg 20 (см. рис. 2.9, д).
Логарифмическая фазовая частотная характеристика, построенная со-
гласно (2.98) в логарифмическом масштабе, приведена на рис. 2.9,
е.

51
ГЛАВА 3.
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ, ЧАСТОТНЫЕ
ХАРАКТЕРИСТИКИ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
И ПРЕОБРАЗОВАНИЕ СТРУКТУРНЫХ СХЕМ
Для получения математического описания характеристик и анализа
статических и динамических свойств системы автоматического управления
любой сложности в ней необходимо выделить типовые динамические зве-
нья направленного действия и выявить взаимосвязь между ними. На осно-
вании установленных связей между звеньями и математического описания
характеристик звеньев составляется структурная схема системы в целом.
При этом
в структурной схеме системы возможны три варианта соедине-
ния звеньев и их комбинация.
3.1. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
ПОСЛЕДОВАТЕЛЬНОГО СОЕДИНЕНИЯ ЗВЕНЬЕВ
Структурная схема n звеньев, соединенных последовательно, приведе-
на на рис. 3.1,
а. Согласно этой схеме можно записать систему уравнений:
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎬
⎫
=
=
=
=
−
−−−
).()()(
);()()(
........................................
);()()(
);()()(
1вых
211
122
вх11
pХpWpХ
pXpWpХ
рХрWpХ
рXpWpX
nn
nnn
(3.1)
Исключив из этой системы промежуточные переменные, получим
)()]()()()([)(
вх121вых
рХpWp.....WpWpWрХ
nn
⋅
⋅
=
−
. (3.2)
52
Следовательно, передаточная функция из n звеньев, соединенных по-
следовательно равна
∏
=⋅⋅==
=
−
n
i
pWpWp.....WpWpW
pX
pХ
pW
inn
1
)()()()()(
)(
)(
)(
121
вх
вых
, (3.3)
т. е. передаточная функция системы последовательно соединенных звеньев
равна произведению передаточных функций звеньев.
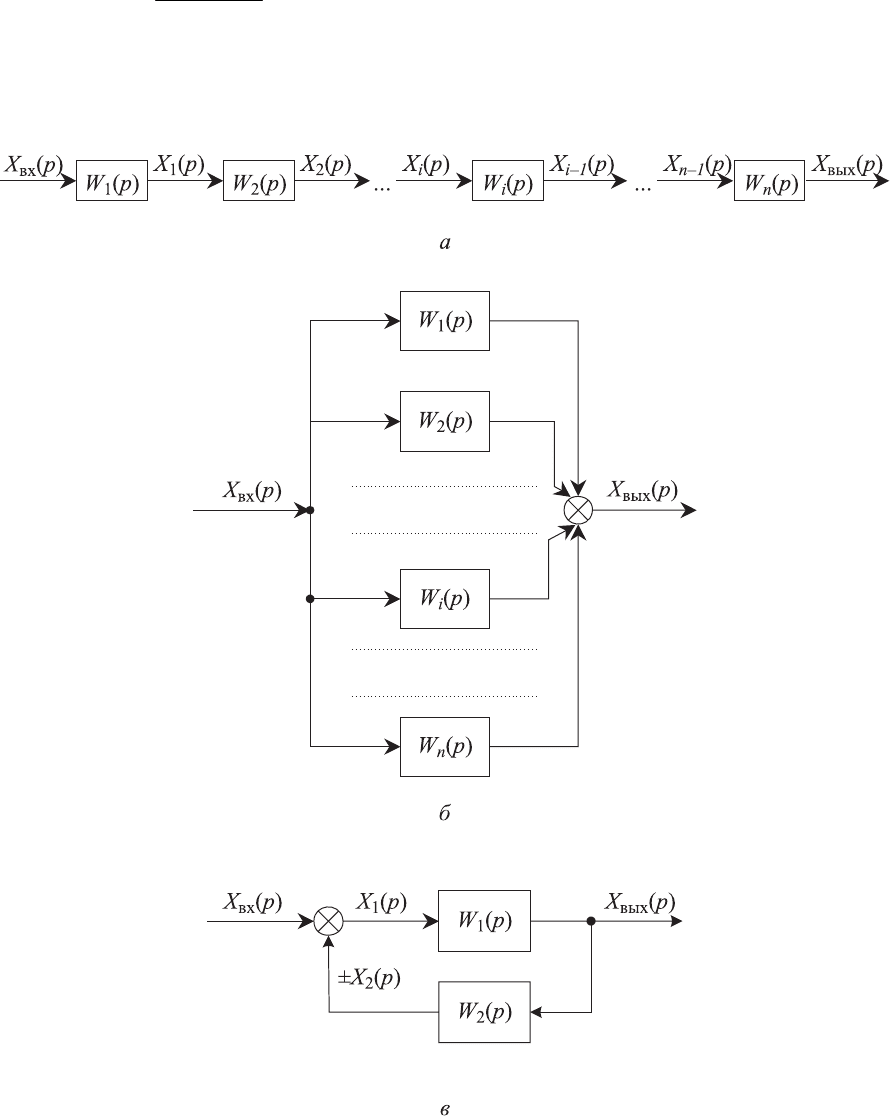
Рис. 3.1. Схемы соединения звеньев:
а — последовательно;
б — параллельно; в — встречно-параллельно
