Динкель А.Д. Теория автоматического управления
Подождите немного. Документ загружается.


53
3.2. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
ПАРАЛЛЕЛЬНО-СОГЛАСОВАННО
СОЕДИНЕННЫХ ЗВЕНЬЕВ
Структурная схема n звеньев, соединенных параллельно согласованно,
приведена на рис. 3.1, б. Из этой схемы следует, что входной сигнал X
вх
(p)
поступает на входы всех звеньев, а результирующий выходной сигнал равен
сумме выходных сигналов звеньев. Согласно этой схеме можно записать
следующую систему уравнений, связывающих выходные и входные сигна-
лы звеньев и системы параллельно согласованно соединенных звеньев:
⎪
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎪
⎬
⎫
++++=
=
=
=
=
=
−
−−
).()()()()(
);()()(
);()()(
..............................
);()()(
);()()(
);()()(
121вых
вх
вх11
вх33
вх22
вх11
pXpX...pXpХpХ
pXpWpХ
pXpWpХ
pXpWpХ
pХpWpХ
pXpWpX
nn
nn
nn
(3.4)
Из этой системы уравнений получаем
)()]()()()([)(
вх121вых
рХр
n
Wр
n
.....WрWрWрХ
+
−
+= . (3.5)
Следовательно, передаточная функция n звеньев, соединенных парал-
лельно-согласованно,
∑
=++==
=
−
n
i
рWрWр.....WрWрW
рX
рХ
рW
inn
1
)()()()()(
)(
)(
)(
121
вх
вых
,(3.6)
т. е. передаточная функция системы параллельно-согласованно соединен-
ных звеньев равна сумме передаточных функций звеньев.

54
3.3. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
ВСТРЕЧНО-ПАРАЛЛЕЛЬНО СОЕДИНЕННЫХ
ЗВЕНЬЕВ
Структурная схема этого варианта включения приведена на рис. 3.1, в.
Согласно этой схеме и принятым обозначениям можно записать следую-
щую систему уравнений:
⎪
⎭
⎪
⎬
⎫
=
=
±=
.XWХ
ХWХ
ХXX
)()()(
);()()(
;)()(
11вых
вых22
2вх1
ppp
ppp
pp
(3.7)
Исходя из этой системы уравнений, получаем
)()]()([1)
вх21
(
вых
рррр XWWХ
⋅
±
=
. (3.8)
Тогда передаточная функция системы встречно-параллельно соеди-
ненных звеньев
)()(1
)(
)(
)(
)(
21
1
вх
вых
рр
р
р
р
р
WW
W
X
Х
W
⋅±
==
. (3.9)
При таком соединении звеньев получается так называемая система
с обратной связью, и сигнал Х
2
(р) является сигналом обратной связи
Х
о.с
(р). Если знак Х
о.с
(р) совпадает со знаком Х
вх
(р), то система является
системой с положительной обратной связью и в знаменателе (3.9) стоит
знак минус, а если знаки противоположные, то система является системой
с отрицательной обратной связью и в знаменателе (3.9) стоит знак плюс.
В общем случае в системе с обратной связью передаточные функ-
ции W
1
(p) и W
2
(p) могут представлять собой передаточные функции
группы звеньев с различными вариантами их соединения.
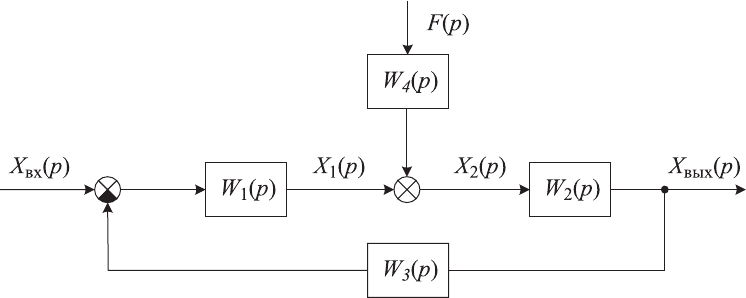
55
3.4. ПРЕОБРАЗОВАНИЕ
СЛОЖНЫХ СТРУКТУРНЫХ СХЕМ
СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Системы с одной или несколькими обратными связями называются
замкнутыми системами автоматического управления. В зависимости от чис-
ла обратных связей, образующих контуры управления, замкнутые системы
автоматического управления делятся на одноконтурные и многоконтурные.
В общем случае, независимо от сложности на систему действуют
управляющие и возмущающие воздействия, которые и определяют ее со-
стояние.
Прежде
чем приступить к исследованию, анализу и расчету сложных
систем автоматического регулирования, их структурные схемы, как прави-
ло, необходимо преобразовать и привести к эквивалентной одноконтурной
схеме, вид которой, в общем случае, представлен на рис. 3.2.
Рис. 3.2. Структурная схема одноконтурной системы управления
Анализ как одноконтурных, так и многоконтурных замкнутых систем
осуществляется на основе их передаточных функций. Передаточная функ-
ция одноконтурной системы определяется достаточно просто с учетом ме-
тодов определения передаточных функций группы звеньев при различных
схемах их соединения. Для того чтобы определить передаточную функцию
многоконтурной системы, последнюю необходимо привести к эквивалент-
ной ей
одноконтурной системе. При этом многоконтурная система, в об-
щем случае, может содержать произвольное число внутренних контуров,
некоторые из которых взаимосвязаны друг с другом, т. е. в системе имеют-
ся так называемые перекрещивающиеся связи.
56
Получить передаточную функцию такой многоконтурной системы
возможно двумя путями. Первый путь — предварительное преобразование
структурной схемы многоконтурной системы в эквивалентную ей струк-
турную схему одноконтурной системы, второй — применение готовой
формулы для передаточной функции замкнутой системы произвольной
сложности.
Первый путь более нагляден и удобен в инженерной практике анализа
сложных многоконтурных систем. В
связи с этим остановимся на рассмот-
рении этого пути получения передаточной функции сложной многокон-
турной системы.
При преобразовании структурных схем сложных многоконтурных
систем, имеющих в своей структуре различные схемы соединения отдель-
ных звеньев и перекрещивающиеся связи, необходимо, во-первых, очередь
использовать изложенные выше способы определения передаточных
функций группы звеньев при различных
схемах их соединения, а во-
вторых, освободиться от перекрещивающихся связей, что связано с пере-
носом точек суммирования сигналов и точек съема сигналов. Перенос этих
точек связан с соблюдением следующих правил:
1.
При переносе точки суммирования сигналов через звено или группу
звеньев по направлению прохождения сигнала, суммирующий сигнал не-
обходимо умножить на передаточную функцию звена или группы звеньев,
через которые переносится точка суммирования (рис. 3.3, б).
2.
При переносе точки суммирования сигналов через звено или группу
звеньев встречно направлению прохождения сигнала, суммируемый сиг-
нал необходимо разделить на передаточную функцию звена или группы
звеньев, через которые переносится точка суммирования (рис. 3.3, в).
3.
При переносе точки съема сигнала через звено или группу звеньев
по направлению прохождения сигнала, снимаемый сигнал необходимо
разделить на передаточную функцию звена или группы звеньев, через ко-
торые переносится точка съема сигнала (рис. 3.4, б).
4.
При переносе точки съема сигнала через звено или группу звеньев
встречно направлению прохождения сигнала, суммируемый сигнал необ-
ходимо умножить на передаточную функцию звена или группы звеньев,
через которые переносится точка съема сигнала (рис. 3.4, в).
5.
Точку суммирования нельзя переносить через точку съема сигна-
лов, как и точку съема сигнала нельзя переносить через точку суммирова-
ния сигналов.
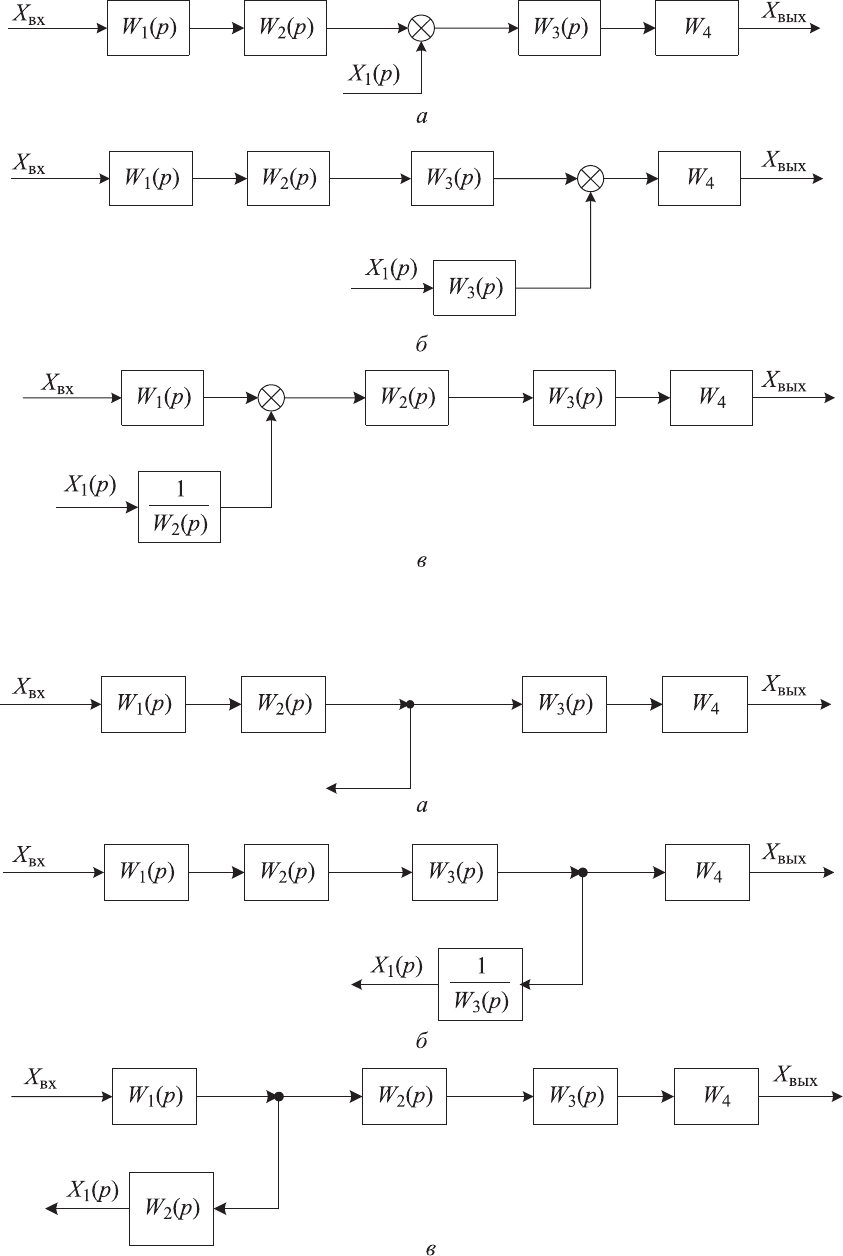
57
Рис. 3.3. Перенос точки суммирования сигналов: а — исходная схема; б — через
звено по направлению сигнала; в — через звено встречно направлению сигнала
Рис. 3.4. Перенос точки съема сигналов: а — исходная схема; б — через зве-
но по направлению сигнала; в — через звено встречно направлению сигнала

58
Рис. 3.5. Примеры преобразования структурных схем (см. также с. 59 и 60)
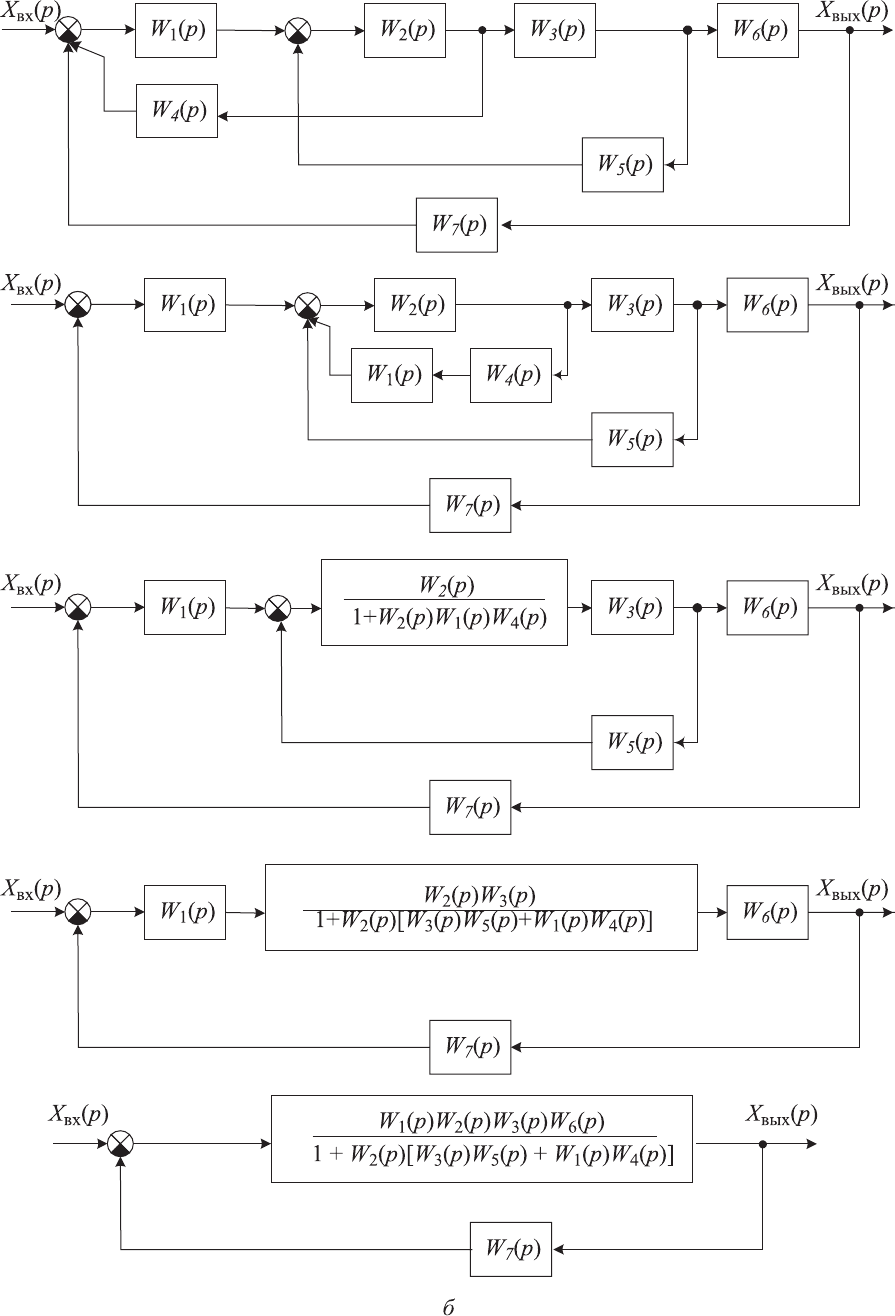
59
Рис. 3.5. Продолжение

60
Рис. 3.5. Окончание
Примеры преобразования сложных структурных схем систем автома-
тического управления на основе изложенных правил приведены на рис. 3.5.
При этом возмущения, действующие на систему приняты нулевыми.
В ряде случаев возникает необходимость приведения сложной систе-
мы автоматического управления к системе с одиночной регулирующей об-
61
ратной связью. Эта необходимость возникает при построении логарифми-
ческих частотных характеристик многоконтурной системы по логарифми-
ческим частотным характеристикам одноконтурной системы.
Последовательность преобразования исходной многоконтурной струк-
турной схемы в эквивалентную ей одноконтурную структурную схему при
переносе точки суммирования через звено по направлению прохождения
сигнала показана на рис. 3.5, а, и при переносе
точки суммирования через
звено против направления прохождения сигнала показана на рис. 3.5, б.
На рис. 3.5, в показана последовательность преобразования структур-
ной схемы при переносе точки съема сигнала по направлению прохожде-
ния сигнала.
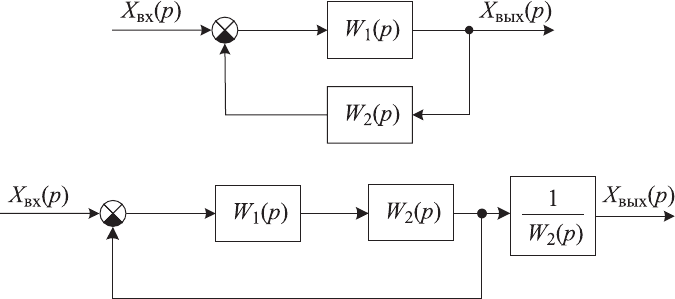
Рис. 3.6. Пример приведения исходной структурной схемы
к схеме с единичной обратной связью
В ряде случаев возникает необходимость приведения замкнутой сис-
темы автоматического управления с неединичной обратной связью к сис-
теме с единичной обратной связью. Эта необходимость возникает при по-
строении логарифмических частотных характеристик замкнутой системы
по логарифмическим частотным характеристикам разомкнутой системы
и обратно, а также при исследовании точностных характеристик системы.
Пример приведения замкнутой
системы с неединичной обратной связью
к системе с единичной обратной связью приведен на рис. 3.6.

62
3.5. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СЛОЖНЫХ
СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Для анализа динамических свойств и расчета систем автоматического
управления широко используются их различные частотные характеристики.
Как показано выше, любая многоконтурная система путем последова-
тельных структурных преобразований может быть приведена к эквива-
лентной ей одноконтурной системе. По полученной структурной схеме эк-
вивалентной одноконтурной системы можно определить передаточную
функцию системы как в разомкнутом
, так и в замкнутом состоянии, пред-
ставляющую собой отношение полиномов от р числителя и знаменателя.
Далее, подставляя в передаточную характеристику р = jω, получим ком-
плексные частотные характеристики разомкнутой и замкнутой системы
W(jω). Выделяя в комплексных частотных характеристиках вещественные
и мнимые составляющие, определим соответственно вещественные R(jω)
и мнимые
I(jω) частотные характеристики. Исходя из этих характеристик
найдем амплитудно-частотные А(ω) и фазочастотные θ(ω) характеристики:
) (ω) (ωω)() (ω
22
IRjWА +==
; (3.10)
) (ω
) (ω
arctgω)(arctg) θ(ω
R
I
jW ==
. (3.11)
Изменяя частоту в пределах 0 ≤ ω ≤ ∞, можно построить графики харак-
теристик R(jω), I(jω), А(ω), θ(ω), а в координатах R(jω), I(jω) — амплитудно-
фазовые частотные характеристики разомкнутой и замкнутой системы.
Для получения логарифмических частотных характеристик необходи-
мо полиномы числителя и знаменателя передаточной
функции разложить
на сомножители, в результате чего получим
()
()
()
1
1
=
=
∏
=
∏
m
l
l
n
i
i
Wp
W р K
Wp
, (3.12)
где W
l
(p) и W
i
(p) — передаточные функции типовых звеньев, получаемых в
результате разложения полиномов.
Следовательно, комплексные частотные характеристики
