Динкель А.Д. Теория автоматического управления

Подождите немного. Документ загружается.

183

В соответствии с вышесформулированным п. 2, значение решетчатой

функции

х[n] = n, n = 1, 2, 3,…,

и в абсолютных единицах времени

х(nT) = nT,

откуда нетрудно увидеть, что

x(t) = t,

что соответствует табл. 8.1.

Введение понятия передаточной функции импульсной системы по

аналогии с понятием передаточной функции непрерывной системы в зна-

чительной мере облегчает исследование импульсных систем автоматиче-

ского регулирования.

Структурную схему замкнутой импульсной линейной системы автома-

тического регулирования с одним импульсным элементом можно, как ука-

зывалось выше, представить в виде соединенных

последовательно импульс-

ного элемента и линейной части, охваченных обратной связью (рис. 8.5).

Рис. 8.5. Схема замкнутой системы импульсного регулирования

Если на вход непрерывной линейной части подается прямоугольный

единичный импульс длительностью γ

в момент времени

iTt

(рис. 8.6), то на ее выходе будет сигнал, который в зависимости от

t имеет

следующее значение:

⎩

⎨

⎧

−−−−

−

=−

)()(

)(

)(ω

ипп

пвых

γTtiThtiTh

tiTh

tiT

при

,∞≤≤+

≤

itТiT

ТiTtiT

пп

ппп

,γ

(8.16)

или в относительных единицах времени

⎩

⎨

⎧

−−−−

−

=−

γ)τ()(

)(

)τω(

ihτih

τih

при

,τγ

γ,τ

∞≤≤+

+≤≤

(8.17)

где

h — переходная функция.

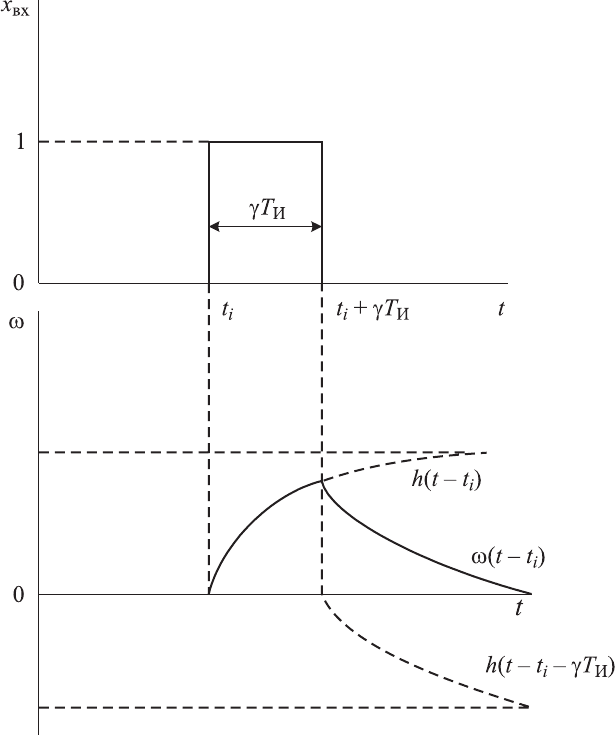
184

Рис. 8.6. Прохождение единичного импульса

в импульсной системе

Практически это выражение описывает переходную импульсную ха-

рактеристику непрерывной части системы регулирования.

Если на вход непрерывной части системы в дискретные моменты вре-

мени

i = 1, 2, 3,… поступает сигнал в виде последовательности прямо-

угольных импульсов с скважностью γ и амплитудой, равной

вх

(i), то, с

учетом метода суперпозиции, результирующая величина выходного сигна-

ла будет равна сумме выходных сигналов, возникающих от каждого

импульса, т. е.

∑

−=

tiTiTхKnTх

)( )ω()(

пвхипвых

(8.18)

или

185

∑

−=

.iniхKnх

)ω( ][][

вхивых

(8.19)

Переходя в (8.19) от оригиналов к изображениям на основе дискрет-

ного преобразования Лапласа, получим

∑

−=

iniх(q)Х

]}.[ ]ω[Д{

вхи

вых

K (8.20)

Используя теорему свертывания, формулу (8.20) можно записать иначе:

]}.ω[]}Д}[Д{

ивх

вых

nKnх(q)Х =

(8.21)

Учитывая, что

∑

∞

−

nKnK

nх(q)Х

,]ω[]}ω[Д{

]},[Д{

ии

вх

из (8.21) получим дискретную передаточную функцию непрерывной ли-

нейной части системы в следующем виде:

∑

∞

−

e]ω[

вх

вых

(q)Х

(q)W , (8.22)

или, используя

Z-преобразование, запишем выражение (8.22) следующим

образом:

∑

∞

−

e]ω[

вх

вых

(z)Х

(z)W

. (8.23)

Таким образом, получена дискретная передаточная функция непре-

рывной линейной части системы.

Для того чтобы получить дискретную передаточную функцию ра-

зомкнутой импульсной системы необходимо учесть передаточную функ-

цию формирующего звена (8.7).

Импульсную замкнутую систему можно привести к виду, показанно-

му на рис. 8.7. Тогда с учетом (8.7) передаточная функция приведенной

непрерывной части

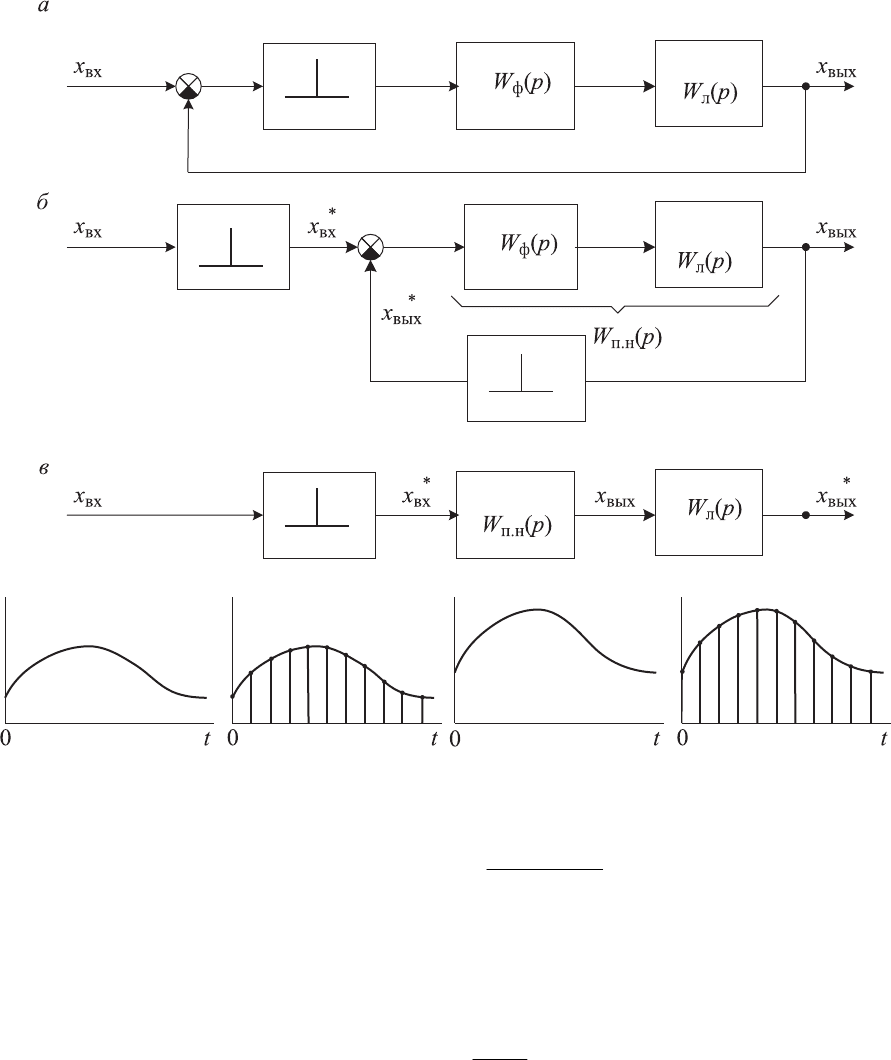
186

Рис. 8.7. Структурная схема импульсной системы и ее преобразование

(р)W

(р)(р)WW(р)W

лфпн

⋅

−

. (8.24)

Учитывая, что переходную характеристику непрерывной системы

можно представить как

⎥

⎦

⎤

⎢

⎣

⎡

−

W(p)

Lh(t)

, (8.25)

тогда (8.24) запишется в следующем виде

].[)(1

пн

e h(t)L(р)W

Tp−

−= (8.26)

Исходя из структурной схемы разомкнутой системы (см. рис. 8.7,

б),

представим ее дискретную передаточную функцию с учетом (8.26) как отно-

187

шение изображения решетчатой функции выходного сигнала

(q)Х

вых

к изображению решетчатой функции входного сигнала

(q)Х

вх

, приняв γ = 1:

)},(Д{

]}[)Д{(1

вх

вых

рТ

h(t)L

(q)Х

(q)W

−

=−==

−

(8.27)

переходя к

Z-преобразованию, получим

}.{

вх

вых

h(t)z

(z)Х

(z)W

−

Любую передаточную функцию можно получить из разностного

уравнения (8.11), применив к нему дискретное преобразование Лапласа

aza...zaza

bzb...zbzb

(z)Х

(z)W

++++

−

вх

вых

. (8.28)

По аналогии с непрерывными системами дискретная передаточная

функция замкнутой импульсной системы автоматического регулирования

(z)W

1 +

= . (8.29)

Дискретные передаточные функции

W(q) и W(z) могут определяться

по передаточным функциям непрерывных систем

W(p) с помощью таблиц

соответствия, которые приводятся в специальной литературе по импульс-

ным системам.

На основании вышеизложенного можно отметить, что импульсная

система с линейной непрерывной частью и импульсным элементом с ам-

плитудно-импульсной модуляцией описывается линейными уравнениями,

т. е. является линейной. В соответствии с этим получены выражения для

дискретной передаточной функции.

188

8.3. УСЛОВИЕ И КРИТЕРИИ

УСТОЙЧИВОСТИ ИМПУЛЬСНЫХ СИСТЕМ

Динамические свойства импульсных систем с амплитудно-

импульсной модуляцией во многом аналогичны динамическим свойствам

непрерывных систем. Поэтому методы анализа таких импульсных систем

являются аналогами соответствующих методов исследования непрерыв-

ных систем.

Устойчивость импульсной системы автоматического регулирования,

как и устойчивость непрерывной системы, определяется характером ее

свободного движения. Следовательно, импульсная система устойчива, ес-

ли свободная

составляющая переходного процесса с течением времени за-

тухает, т. е. если

0lim

∞→

(iT)х

. (8.30)

Как и у непрерывных систем, в импульсной системе свободная со-

ставляющая переходного процесса определяется знаменателем передаточ-

ной функции замкнутой системы:

(q)Q

(q)P

(q)W

= . (8.31)

Следовательно, для выполнения условия устойчивости (8.30) необхо-

димо, чтобы все корни характеристического уравнения

eee

1)(

=++++=

−

mqqm

cc...cc(q)Q (8.32)

располагались в левой полуплоскости комплексной плоскости

При Ωω

jTjq ±=±= , функция е

является периодической функци-

ей вдоль мнимой оси, т. к.

) кπ 2(ΩΩ

eee

+±±

jjq

, (8.33)

Ω — частота, в относительных единицах.

Поэтому нет необходимости рассматривать расположение всех корней

комплексной плоскости

q, а достаточно рассматривать их расположение в

полосе

±π вдоль мнимой оси.

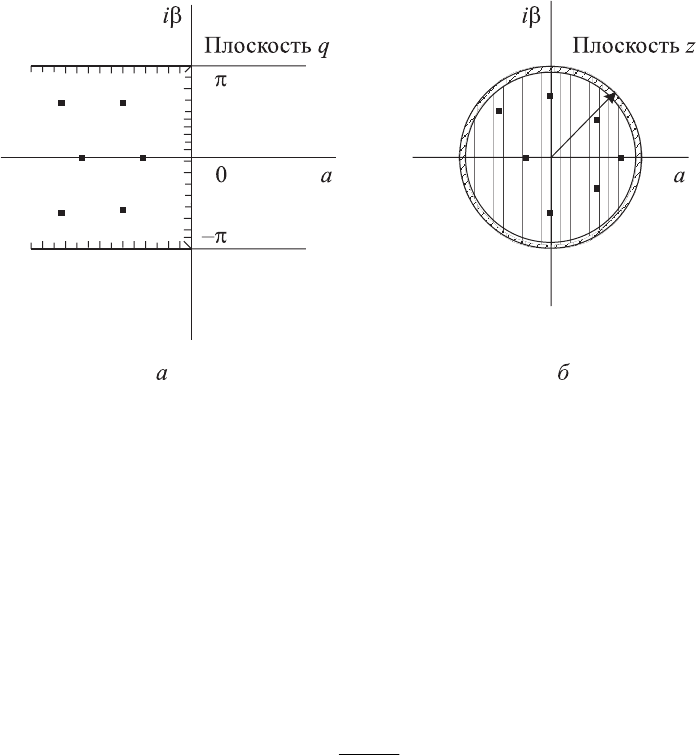
189

Таким образом, замкнутая импульсная система будет устойчивой, ес-

ли корни ее характеристического уравнения при изменении

Ω от –π до +π

будут расположены в полосе

±π левой полуплоскости комплексной плос-

кости

q (рис. 8.8, а).

Если перейти от

q к z = e

, то характеристическое уравнение замкну-

той системы можно записать в следующем виде:

=++++=

−

cz c...zczc(z)Q (8.34)

где

— расстояние величины, определение физическими свойствами сис-

темы и нахождение корней уравнения (8.32) в полосе

±π левой полуплос-

кости комплексной плоскости

q соответствует нахождению корней урав-

нения (8.34) внутри окружности радиусом, равным единице, с центром в

начале координат комплексной плоскости

z (см. рис. 8.8, б). Эта окруж-

ность является границей устойчивости.

Рис. 8.8. Расположение корней характеристического уравнения

импульсной устойчивой системы в плоскостях q и z

Следовательно, в этих случаях для суждения об устойчивости им-

пульсной системы требуется вычислять корни характеристического урав-

нения, что связано с известными трудностями для систем выше третьего

порядка.

Чтобы избежать процесса вычисления корней, характеристическое

уравнение (8.34) преобразуется подстановкой

1ω

−

=z , (8.35)

190

и приводится к некоторому характеристическому уравнению

0dωdωdωd

=++++

−

...

, (8.36)

— постоянные величины.

В результате этого отображением окружности единичного радиуса в

комплексной плоскости

z является мнимая ось комплексной плоскости но-

вой переменной

ω, а границей устойчивости — мнимая ось. Таким обра-

зом, в результате указанной подстановки, т. е. перехода от переменной

z к

переменной

ω получено характеристическое уравнение, условия устойчи-

вости которого совпадают с условиями устойчивости непрерывных систем.

Поэтому к нему непосредственно могут быть применены критерии устой-

чивости линейных непрерывных систем, в частности алгебраические кри-

терии Рауса и Гурвица.

В ряде случаев для определения устойчивости импульсных систем ре-

гулирования более целесообразно использовать частотные критерии, яв-

ляющиеся аналогами частотных критериев, применяемых для определения

устойчивости линейных непрерывных систем, в частности аналоги

критериев Михайлова и Найквиста.

Аналог критерия Михайлова

. Если в характеристическое уравнение

(8.32) подставить

Ω

= , то получим уравнение характеристической

кривой

0)(

Ω

1)Ω(

Ω

eee =++++=

−

mjjm

c c...ccjΩQ

, (8.36)

Так как функция

Ω

является гармонической функцией, то для по-

строения годографа вектора

Ω)(

, являющегося характеристической

кривой Михайлова, достаточно Ω изменять от –

π до +π и при этом изме-

нение аргумента вектора

Ω)(

в устойчивой системе будет равно π2m .

Так как корни характеристического уравнения (8.32) располагаются

симметрично относительно вещественной оси комплексной плоскости

то характеристическую кривую можно строить, изменяя

Ω

от 0 до +π. То-

гда изменение аргумента вектора

Ω)(

в устойчивой системе будет рав-

но π

m .

Учитывая, что в основу критерия устойчивости Михайлова положен

принцип аргумента, его аналог применительно к импульсным системам мож-

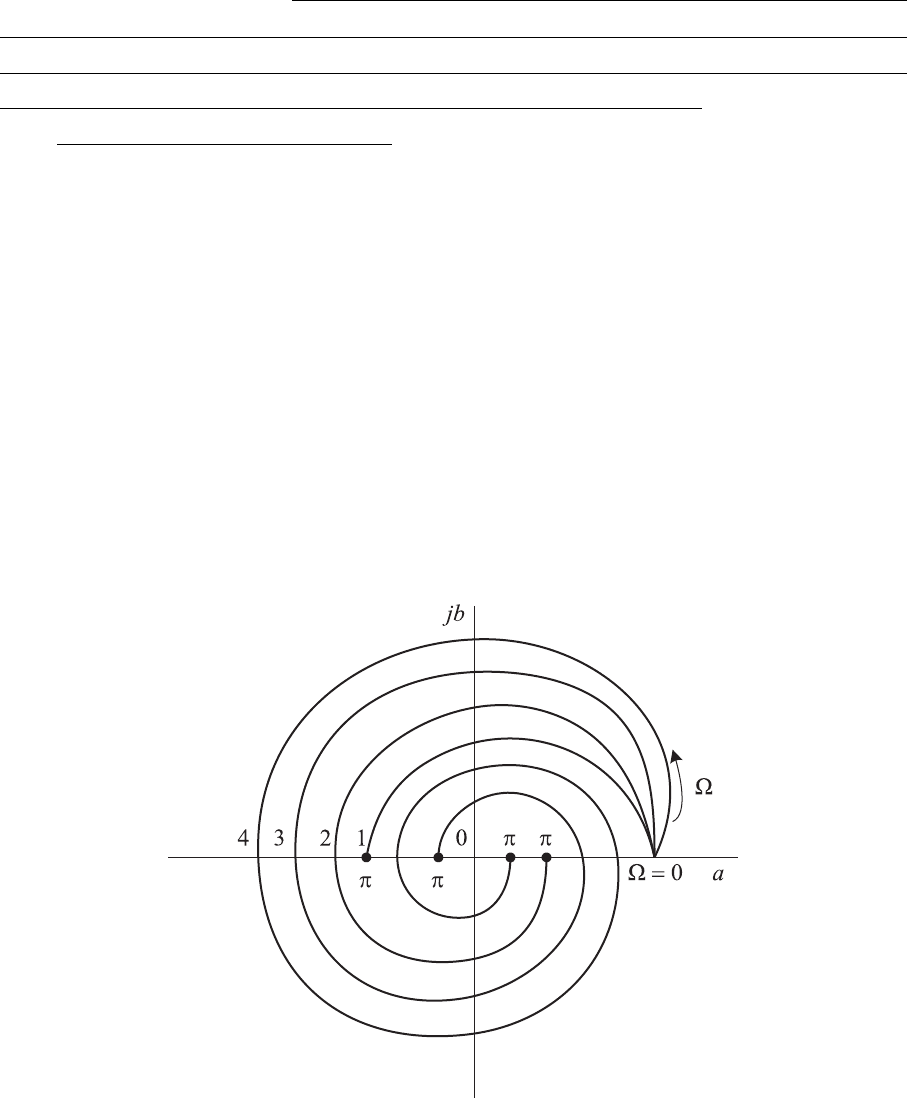
191

но сформулировать так: импульсная система регулирования устойчива, если

при изменении Ω от 0 до +π характеристическая кривая, начинаясь с положи-

тельной части вещественной оси комплексной плоскости q, последовательно

проходит через 2m квадрантов, охватывая начало координат (рис. 8.9).

Аналог критерия Найквиста

. Как известно, об устойчивости замкнутой

системы можно судить по амплитудно-фазовой частотной характеристике

разомкнутой системы. Следовательно, согласно (1.34), учитывая, что

z = e

и принимая Ω

jq = , необходимо получить амплитудно-фазовую частотную

характеристику разомкнутой импульсной системы регулирования:

) (Ω) (ΩΩ)(

***

jIRjW += , (8.38)

) (Ω

R , ) (Ω

I — соответственно импульсная вещественная и импульсная

мнимая части,

и построить ее на комплексной плоскости как годограф вектора

Ω)(

∗

изменяя

Ω от 0 до +π.

Рис. 8.9. Годографы Михайлова для импульсных систем

192

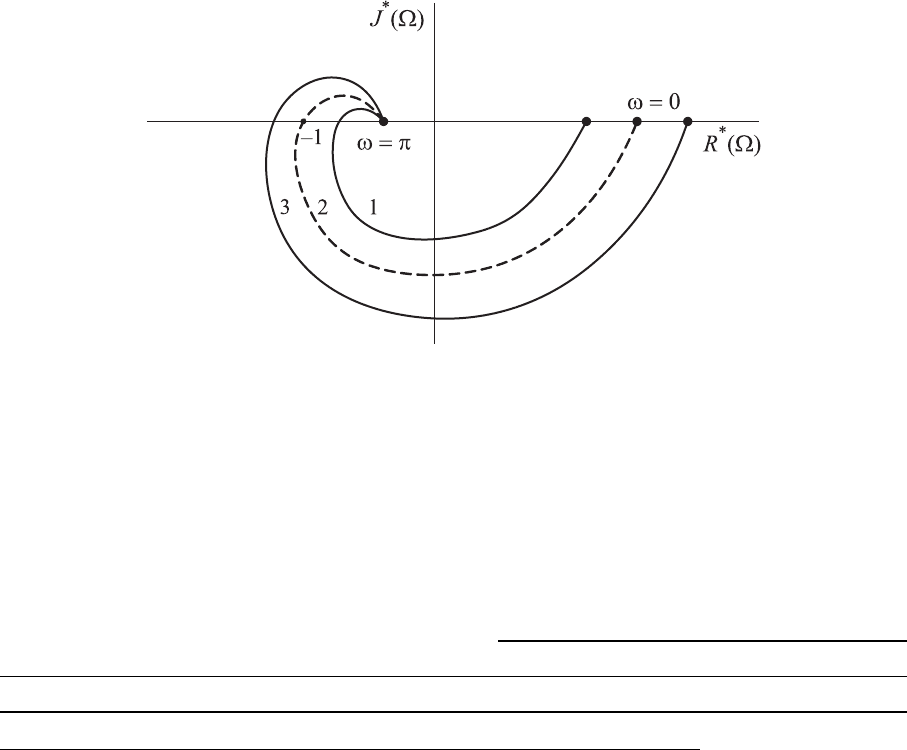
Рис. 8.10. Амплитудно-фазовые частотные характеристики

разомкнутой импульсной системы

при которых замкнутая импульсная система:

1 — устойчива; 2 — находится на границе устойчивости;

3 — неустойчива

Тогда, по аналогии с непрерывными системами, аналог критерия ус-

тойчивости Найквиста применительно к импульсным системам регулирова-

ния формулируется следующим образом: замкнутая импульсная система ре-

гулирования будет устойчивой, если амплитудно-фазовая частотная харак-

теристика этой системы в разомкнутом состоянии не охватывает точку с ко-

ординатами (–1; j0) при изменении Ω от 0 до +π (рис. 8.10).

8.4. ПЕРЕХОДНЫЕ ПРОЦЕССЫ

В ИМПУЛЬСНЫХ СИСТЕМАХ

Характер протекания переходных процессов в замкнутых импульсных

системах автоматического регулирования можно определить как точными

аналитическими, так и приближенными графоаналитическими методами,

аналогичными методам, используемым при исследовании линейных не-

прерывных замкнутых систем регулирования.

Один из аналитических методов базируется на дискретном

преобразовании Лапласа.

Исходя из дискретной передаточной функции замкнутой импульсной

системы (8.31), можно записать следующее

выражение: