Динкель А.Д. Теория автоматического управления

Подождите немного. Документ загружается.

113

Следует отметить, что абсолютные значения любой интегральной

оценки сами по себе не представляют интереса. Они в основном исполь-

зуются для сопоставления вариантов настройки одной и той же системы и

для определения оптимальных значений настроек системы автоматическо-

го регулирования. При этом оптимальными являются настройки, которым

соответствует минимум принятого интегрального показателя.

5.5. КОРНЕВОЙ КРИТЕРИЙ КАЧЕСТВА

Этот критерий оценки качества переходного процесса основан на ис-

пользовании значений полюсов и нулей передаточной функции системы,

т. е. корней знаменателя и числителя, и границ области расположения кор-

ней характеристического уравнения на комплексной плоскости.

Указанный метод позволяет наглядно и достаточно просто оценить

быстродействие замкнутой системы и ее колебательность по границам

расположения

корней характеристического уравнения.

Передаточная функция замкнутой системы автоматического регули-

рования, связывающая выходной сигнал с входным, в общем случае можно

представить в следующем виде:

Q(р)

Р(р)

cpc...pcpc

bpb...pbpb

(p)W

++++

−

. (5.21)

В результате разложения полиномов числителя и знаменателя (5.21)

на сомножители получим

(

)

()

∏

−

∏

−

(p)W

где

λ и

λ — соответственно нули и полюсы передаточной функции.

Нули и полюсы передаточной функции являются корнями уравнений

Р(р) = 0; (5.22)

Q(p) = 0. (5.23)

114

Отсюда видно, что нули и полюсы, т. е. корни уравнений (5.22)

и (5.23), определяют характер переходного процесса, а следовательно,

и качество регулирования.

В частном случае, когда передаточная функция не имеет нулей, пере-

ходный процесс будет определяться корнями характеристического уравне-

ния Q(p) = 0. Исходя из этого, решение уравнения

(р)Х

Q(р)

Р(р)

(p)Х

вхвых

при единичном ступенчатом входном сигналом Х

вх

(t) = [1] запишется в

следующем виде:

∑

(t)х

вых

)(λ

(0)

, (5.24)

где

λ - корни характеристического уравнения (5.13).

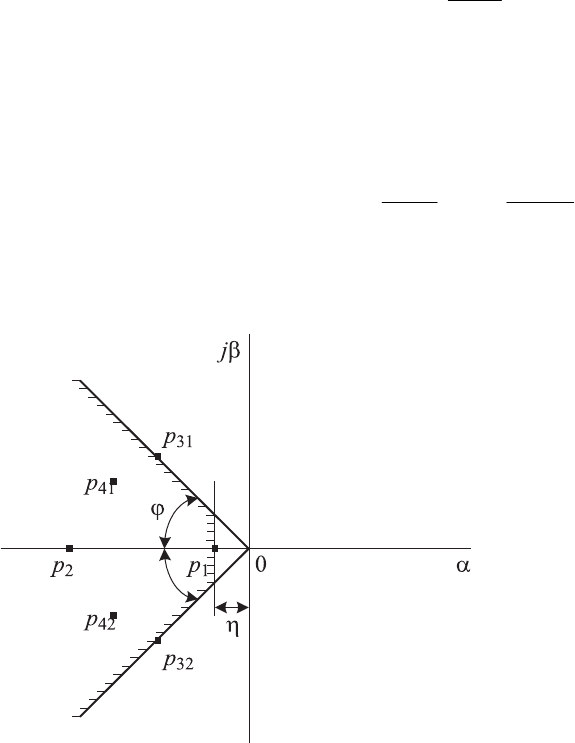
Расположение корней на

комплексной плоскости можно

характеризовать двумя показате-

лями: удалением минимального

вещественного корня или пары

комплексно-сопря-женных кор-

ней с наименьшей вещественной

составляющей от мнимой оси α

и углом 2ϕ, в плоскости которо-

го расположены все корни ха-

рактеристического уравнения,

как это показано на рис

. 5.8.

Расстояние от мнимой оси

до ближайших к ней веществен-

ного или пары комплексно-

сопряжен-ных корней η называ-

ется степенью устойчивости и характеризует длительность протекания пе-

реходного процесса.

Колебательные свойства системы характеризуются углом ϕ, т. е. па-

рой корней, для которых будет наибольшим отношение модулей мнимой и

вещественной составляющих. Это

отношение

Рис. 5.8. Расположение корней ха-

рактеристического уравнения ус-

тойчивой системы

115

ϕ==

µ (5.25)

называют степенью колебательности

Очевидно, что степень колебательности будет определять пара ком-

плексных корней, расположенных на границе области расположения корней.

В общем случае, когда передаточная функция (5.21) имеет нули,

оценка качества процесса регулирования только по полюсам передаточной

функции может дать большую ошибку, как в сторону его ухудшения, так и

в сторону улучшения. Очевидно, что в

этом случае необходимо использо-

вать другие методы оценки качества процесса регулирования.

5.6. СВЯЗЬ ПЕРЕХОДНОГО ПРОЦЕССА

С ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ

СИСТЕМЫ АВТОМАТИЧЕСКОГО

РЕГУЛИРОВАНИЯ

Комплексная частотная характеристика системы автоматического ре-

гулирования выражает взаимосвязь между выходным и входным сигнала-

ми при воздействии на систему гармонического входного сигнала.

Однако в большинстве случаев входной сигнал представляет собой

сложную периодическую или непериодическую функцию. Очевидно, что

при этом связь между выходным и входным сигналами на основе ком-

плексной частотной характеристики

может быть установлена, если вход-

ной сигнал представить в виде гармонических составляющих на основе ря-

да или интеграла Фурье. В дальнейшем, при установлении различных за-

висимостей будем использовать интеграл Фурье

() ()

ω dω

2π

jFtf

∫

∞

∞−

. (5.26)

Если на систему воздействует непрерывный входной сигнал f

вх

(t), то,

согласно преобразованиям Фурье, можно определить его комплексный

спектр

116

() ()

t tfjF

dω

вхвх

−

∫

∞

∞−

. (5.27)

Если на систему автоматического регулирования с комплексной час-

тотной характеристикой

)

W(j ω воздействует входной сигнал с комплекс-

ным спектром

ω)(

вх

то согласно интеграла Фурье сигнал на выходе

() ()()

ωdωω

2π

вхвых

e jW jFtх

∫

∞

−

. (5.28)

Введем новый комплекс

X(jω) = F

вх

(jω) W(jω), (5.29)

который называется обобщенной частотной характеристикой

системы ав-

томатического регулирования. Следовательно

() ()

dωω

2π

вых

jХtх

∫

∞

∞−

. (5.30)

Представим обобщенную частотную характеристику в виде суммы

вещественной и мнимой составляющих:

)(ω)(ω)ω( jQ

jХ

. (5.31)

Учитывая это, можем записать

() () ()

[]

dωωω

2π

вых

jQPtх e

∫

∞

∞−

, (5.32)

или в тригонометрической форме

() () ()

[]

()

() ()

[]

() ()

[]

. t Qt Pj

t Qt P

jQPtх

dωω cos ωωsin ω

2π

dωωsin ωω cos ω

2π

dω ωsin ω cos ωω

2π

вых

∫

−=

∫

∞

−

∞

∞−

∞

∞−

tj t

(5.33)

117

Так как sin(–ωt) = –sin ωt, Q(–ω) = –Q(ω) — нечетные функции; а cos(–

ωt) = cos ωt, P(–ω) = P(ω) — четные функции, то второе слагаемое при ин-

тегрировании в указанных пределах обращается в нуль, в результате полу-

чим

() () ()

[]

dωωsin ωω cos ω

2π

вых

t Qt Ptх

∫

−=

∞

∞−

. (5.34)

Это выражение представляет собой вещественную часть комплексно-

го интеграла Фурье.

В реальных системах при 0

≤

вых

(t)х . Следовательно,

() ()

[]

0dωωsin ωω cos ω

2π

∫

∞

∞−

t Qt P . (5.35)

Складывая (5.34) и (5.35), получим:

() () ()

dωω cos ω

dωω cos

вых

t P t ωPtх

∫

∞∞

∞−

. (5.36)

Вычитая (5.34) и (5.35), получим:

() () ()

dωωsin ω

dω ωsin

вых

t Q t ωQtх

∫

−=

∫

−=

∞∞

∞−

. (5.37)

Таким образом получены выражения, связывающие выходной сигнал

системы автоматического регулирования с вещественной и мнимой частя-

ми обобщенной частотной характеристики этой системы.

Анализ динамических свойств системы автоматического регулирова-

ния, как правило, осуществляется по ее реакции на единичное ступенчатое

входное воздействие, т. е. по переходной характеристике.

Выявим зависимости, аналогичные вышеизложенным при входном

сигнале в виде единичной ступенчатой функции

[1]

вх

(t)f . (5.38)

Тогда изображение этой функции

(р)F

вх

, (5.39)

118

а комплексный спектр входного сигнала

ω)(

вх

jF =

. (5.40)

Следовательно, сигнал на выходе системы с комплексной частотной

характеристикой ω)( jW равен ∞.

()

(

)

dω

2π

вых

tх

∫

∞

∞−

. (5.41)

Представляя

)(ω)(ωω)( j

, (5.42)

исходя из (5.41), получим

()

() ()

()

dω ωsin ω cos

2π

dω

) (ω) (ω

2π

вых

tj t

jIR

tх

∫

⎥

⎦

⎤

⎢

⎣

⎡

−=

∫

∞

∞−

∞

∞−

(5.43)

или

()

(

)

(

)

() ()

вых

ωω

sin ω cos ω dω

2πω ω

ωω

cos ω sin ω dω .

2πω ω

xt t t

jtt

∞

−∞

∞

−∞

⎡⎤

=++

∫

⎢⎥

⎣⎦

⎡⎤

+− +

∫

⎢⎥

⎣⎦

(5.44)

Подынтегральная функция второго слагаемого является нечетной,

следовательно, в результате интегрирования в указанных пределах второе

слагаемое обращается в нуль и

()

() ()

. 0dω ω cos

ωsin

2π

–

вых

⎥

⎦

⎤

⎢

⎣

⎡

∫

∞

tх (5.45)

При 0<

() ()

. 0dω ω cos

ωsin

2π

–

⎥

⎦

⎤

⎢

⎣

⎡

+−

∫

∞

(5.46)

119

Вычитая (5.46) из (5.45), а также изменяя пределы интегрирования,

получим:

()

(

)

вых

sin .

ttd

∞

=ωω

∫

(5.47)

Складывая (5.45) и (5.46) с учетом изменения пределов интегрирова-

ния, получим:

()

. t

tх dω ω cos

вых

∫

∞

= (5.48)

Таким образом получены зависимости для определения переходной

характеристики по вещественной или мнимой составляющим комплексной

частотной характеристики системы автоматического регулирования, т. е.

по вещественной или мнимой частотным характеристикам замкнутой

системы автоматического регулирования.

Вещественную или мнимую частотную характеристику замкнутой

системы автоматического регулирования можно получить расчетным пу-

тем по комплексной частотной характеристике замкнутой

системы или

с помощью номограмм с использованием логарифмических амплитудной

и фазовой частотных характеристик разомкнутой системы.

В практике расчета и проектирования систем автоматического регу-

лирования, как правило, используются вещественные частотные характе-

ристики.

Рассмотрим аналитическую связь между вещественной частотной ха-

рактеристикой замкнутой системы и логарифмическими амплитудной

и фазовой частотными характеристиками.

Запишем комплексную

частотную характеристику разомкнутой сис-

темы с единичной обратной связью в тригонометрической форме:

()

(

)

[

]

разразразраз

θsin θ cosωω j AjW += . (5.49)

Тогда для замкнутой системы

()

(

)

(

)

() ()

разразразраз

разразразразраз

раз

θsin ωθ cos ω1

θsin ωθ cos ω

ω1

раз

Aj A

= . (5.50)

120

Разделяя правую часть этой зависимости на вещественную и мнимую

составляющие, получим выражение для вещественной частотной характе-

ристики замкнутой системы:

1θ cos ) (ω2) (ω

θ cos ) (ω) (ω

) (ω

разраз

раз

разраз

раз

АА

AА

R . (5.51)

Задаваясь постоянными значениями

const)(ω

R ,

по (5.51) можно получить зависимость

(

)

раз раз

(ω ) θ

Af= ,

согласно которой можно построить семейство кривых в координатах

) (ω lg 20) (ω

раз

AL = в децибелах и )(

в градусах. Каждая кривая из

этого семейства является геометрическим местом точек const)(ω =

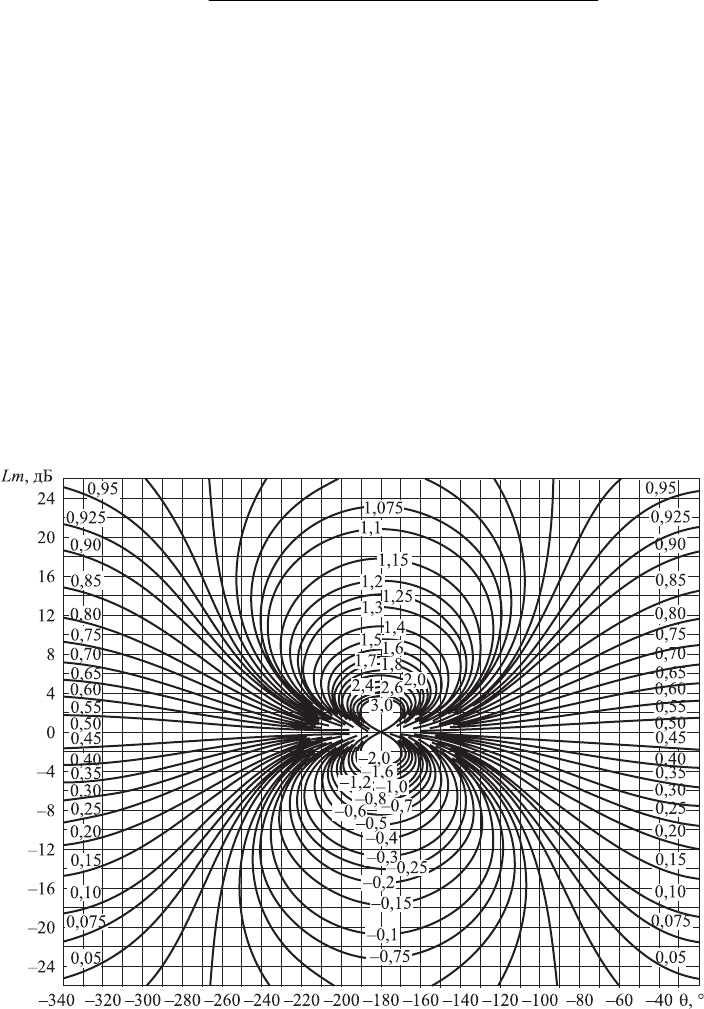
Рис. 5.9. Номограммы для определения по логарифмическим ам-

плитудной и фазовой частотным характеристикам разомкнутой

системы вещественной частотной характеристики замкнутой сис-

темы в линейном масштабе

121

Это семейство кривых по сути своей номограмма (рис. 5.9), по кото-

рой определяется вещественная частотная характеристика замкнутой сис-

темы автоматического регулирования с единичной обратной связью по ло-

гарифмическим амплитудной и фазовой частотным характеристикам ра-

зомкнутой системы. Необходимо подчеркнуть, что логарифмические час-

тотные характеристики разомкнутой системы должны быть построены ис-

ходя из

системы с единичной обратной связью.

5.7. ПРИБЛИЖЕННЫЙ МЕТОД ПОСТРОЕНИЯ

ПЕРЕХОДНОГО ПРОЦЕССА ПО ВЕЩЕСТВЕННОЙ

ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ РАЗОМКНУТОЙ

СИСТЕМЫ АВТОМАТИЧЕСКОГО

РЕГУЛИРОВАНИЯ

Приближенный метод построения переходного процесса базируется

на исходной зависимости

()

(

)

вых

sin ω d ,

πω

ttt

∞

∫

(5.52)

в которой используется кусочно-линейно аппроксимированная веществен-

ная частотная характеристика R

(ω). При этом возможны два способа ап-

проксимации R

(ω), а следовательно, и два подхода к построению пере-

ходного процесса.

При первом способе R

(ω) аппроксимируется линейными отрезками в

определенных диапазонах частот в зависимости от характера изменения

(ω) и желаемой точности. Для каждого из линейных участков R

(ω) дает-

ся его математическое описание и по (5.52) определяется составляющая

переходного процесса. Результирующая кривая переходного процесса сис-

темы определяется путем суммирования ординат всех его составляющих

при соответствующих значениях частоты.

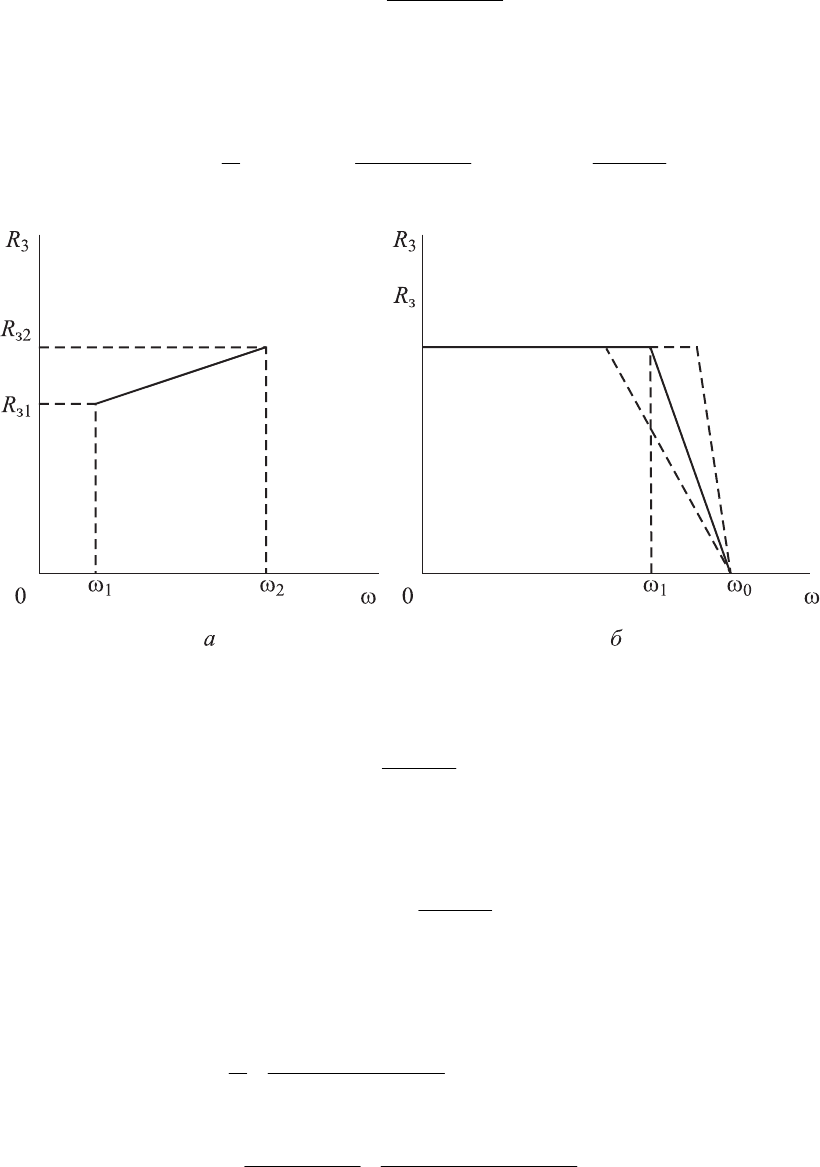
Рассмотрим ход построения составляющей переходного процесса для

одного линейного участка R

(ω), представленного на рис. 5.10, а. Для этого

участка можем записать

122

)ω(ω

ωω

) (ω

з1з2

з1з

−

RR . (5.53)

Тогда согласно (5.52) получим

()

ω d

ωsin

)ω(ω

ωωπ

з1з2

з1вых

Rtx

∫

⎥

⎦

⎤

⎢

⎣

⎡

−

∞

. (5.54)

Рис. 5.10. Характеристика

(ω): а — линейная; б — трапециевидная

Ввиду того, что интеграл ω d

tωsin

∫

∞

классическими методами не

вычисляется, введено понятие интегрального синуса

∫

∞

ω d

ωsin

) , (ω

. (5.55)

В соответствии с этим (5.54) запишется в следующем виде:

()

()()

[]

⎪

⎭

⎪

⎬

⎫

−

⋅

−

⎪

⎩

⎪

⎨

⎧

−−

−

з1з2

1з22з1

вых

ω cosω cos

ωω

,ω,ω

ωω

. (5.56)

По этому выражению с использованием табличных значений ),(ω tS

строится составляющая переходного процесса. Выполнив аналогичным