Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing
Подождите немного. Документ загружается.

1128 Part E Modeling and Simulation Methods
a)
(1)
4
3
2
1
1234(1)
b)
(1)
4
3
2
1
1234(1)
c)
(1)
4
3
2
1
1234(1)
d)
(1)
4
3
2
1
1234(1)
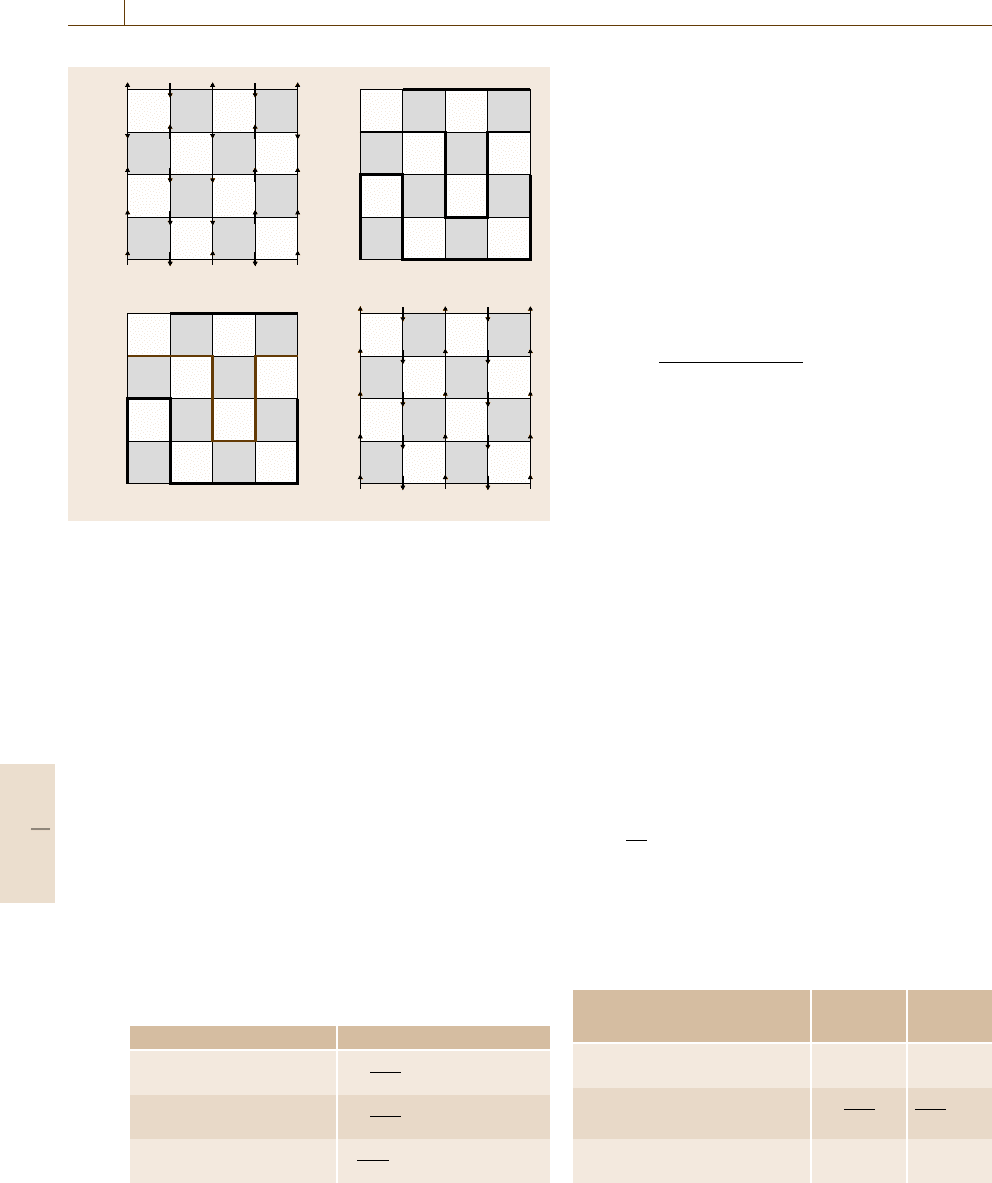
Fig. 22.6a–d Update of spin configurations through graph repre-
sentation. See text for details
The updating procedure in the cluster algorithm
is illustrated in Fig. 22.6: For a spin configuration
Fig. 22.6a, graphs are assigned as in Fig. 22.6b with
probability given in (22.56), which results in clus-
ters (or loops). The clusters are flipped with prob-
ability 1/2. If the graph shown in a red line in
Fig. 22.6c is flipped, the spin configuration becomes
as in Fig. 22.6d. In the cluster algorithm, a large
number of spins flip simultaneously. Hence, the auto-
correlation time is greatly reduced compared with
the world-line algorithm [22.40, 70, 71]. Also, it
is easy to take the limit of Δτ → 0 [22.72]. For
isotropic Heisenberg models and XXZ models with
XY-anisotropy, clusters form loops. Hence, the cluster
algorithm for these models are called the loop algo-
rithm [22.40].
Table 22.3 Local configurations and their weights in the
limit of Δτ →0
a w(a)
↑↑
↑↑
,
↓↓
↓↓
1 −
Δτ J
4
↑↓
↑↓
,
↓↑
↓↑
1 +
Δτ J
4
↑↓
↓↑
,
↓↑
↑↓
−
Δτ J
2
The cluster algorithm is also applied to the mod-
els with general spin S [22.73]. Since spin-S operators
can be represented by 2S spin-1/2 operators, simula-
tions in the N
s
-site system with spin S can be performed
by mapping the system onto the 2SN
s
-site system with
spin-1/2 operators under the special boundary condition
in the imaginary-time direction [22.74]. The boundary
condition is set in order to project out the unphysical
states with S
2
i
< S(S +1).
Simulations under the magnetic field (H) can be
performed by the cluster algorithm, replacing the flip-
ping probability with
P
flip
=
e
β HM
new
e
β HM
new
+ e
β HM
old
, (22.57)
where M
new
and M
old
are the magnetizations of the
cluster in the new and old configurations, respectively.
We should be careful about the use of it in the low-
temperature regime under high magnetic fields, because
in such situations the flipping probability defined in
(22.57) becomes exponentially small [22.75]. Hence,
in this case, other algorithms such as the worm algo-
rithm [22.76,77] or the directed-loop algorithm [22.78]
are suitable.
22.3.4 Continuous-Time Algorithm
Based on the cluster algorithm, the limit of Δτ →0is
taken [22.72]. The local weights in Table 22.1 become
as in Table 22.3 in the limits of Δτ →0. The probabil-
ity of assigning graphs P(g|a)isgiveninTable22.4,
using (22.56). The positions of new vertices are statis-
tically determined in the continuous time. According
to Table 22.4, the probability that a new vertex is cre-
ated during the interval τ
L
between antiparallel spins is
1− e
−
τ
L
J
2
. The procedure of the continuous-time loop
algorithm is illustrated in Fig. 22.7: For a spin configu-
ration Fig. 22.7a, graphs are assigned as in Fig. 22.7b
with probabilities given in Table 22.4. The loops are
Table 22.4 Probability P(g|a) of assigning graphs to con-
figurations in the limit of Δτ →0.
a
-
g
||
||
↑↑
↑↑
,
↓↓
↓↓
1 0
↑↓
↑↓
,
↓↑
↓↑
1 −
Δτ J
2
Δτ J
2
↑↓
↓↑
,
↓↑
↑↓
0 1
Part E 22.3

Monte Carlo Simulation 22.3 Quantum Monte Carlo Method 1129
flipped with probability 1/2. If the graphs shown in
red lines in Fig. 22.7c are flipped, the spin configuration
becomesasinFig.22.7d.
Physical quantities are calculated in the same way
as in the discrete-time loop algorithm. Since in the
continuous-time algorithm, the limit of Δτ →0isal-
ready taken, it is unnecessary to extrapolate data to
Δτ →0. Another merit is that the memory cost is gen-
erally smaller than the discrete-time loop algorithm.
The stochastic series expansion (SSE) algo-
rithm [22.79–81] is an alternative quantum Monte Carlo
algorithm which does not depend on the Trotter for-
mula and can produce exact results within error bars
without extrapolations at finite temperatures. In the SSE
algorithm, the partition function defined in (22.49)is
expressed as
Z =
∞
n=0
(−β)
n
n!
TrH
n
. (22.58)
This expansion converges exponentially for n ∼ N
s
β.
Here, a truncation at n = L of this order is imposed. The
number L is adjusted during equilibration so that the
highest value of n appearing in the simulation does not
exceed L. In this case, truncation errors become com-
pletely negligible. Using this L, the partition function is
rewritten as
Z =
S
L
β
m
(L −m)!
L!
Tr
L
i=1
H
a
i
,b
i
, (22.59)
where S
L
denotes a sequence of operator indices:
S
L
=[a
1
, b
1
], [a
2
, b
2
], ···, [a
L
, b
L
], with a
i
∈{1, 2}
and b
i
∈{1, ···, M} (M: the number of bonds), or
[a
i
, b
i
]=[0, 0]. Here, H
1, j
and H
2, j
denote diagonal
and off-diagonal parts of the local Hamiltonian on bond
j, respectively. (A positive constant is added to H
1, j
in order to make all matrix elements positive, if neces-
sary.) The operator H
0,0
is defined as the unit operator:
H
0,0
=1. The number of non-[0,0] elements in S
L
is
denoted by m. Simulations are performed in the N
s
L
site system in the (d +1)-dimensional space-time. Spin
configurations are updated through updates of indices at
vertices [1, b]↔[0, 0]or [1, b
i
][1, b
j
]↔[2, b
i
][2, b
j
].
The latter process is improved by the operator-loop
update [22.82], which is naturally extended to the
directed-loop algorithm [22.78].
22.3.5 Worm Algorithm
In the cluster algorithm, it is difficult to investigate
properties in the low-temperature regime under high
a)
1234(1)
b)
1 2 3 4 (1)
c)
1234(1)
d)
1 2 3 4 (1)
Fig. 22.7a–d Update of spin configurations through graph repre-
sentation in the limit of Δτ →0. In (a) and (d), up and down spins
are represented by solid and dotted lines, respectively. In (b),new
vertices are joined by red lines. See text for details
a)
1234(1)
b)
1234(1)
c)
1234(1)
d)
1234(1)
Fig. 22.8a–d Update of spin configurations by the directed-loop
algorithm
magnetic fields, because the flipping probability of clus-
ters becomes exponentially small. This difficulty can
be removed by taking the effects of magnetic fields
Part E 22.3

1130 Part E Modeling and Simulation Methods
into account in the process of loop formations, as
in the worm algorithm [22.76, 77] and the directed-
loop algorithm [22.78]. The updating procedure of
the directed-loop algorithm is illustrated in Fig. 22.8:
A starting point is randomly choosen in the (d +1)-
dimensional space-time as in Fig. 22.8a. From this
starting point, the worm moves in one of the two di-
rections as in Fig. 22.8b. The worm can hop to another
site stochastically as in Fig. 22.8c. Reaching a vertex,
the worm jumps to the other site as in Fig. 22.8d with
the probability one. These motions are continued until
the worm goes back to the starting point. (The worm
may turn back at vertices, if probabilities are defined to
allow such processes.) The trajectory of the worm forms
a loop as in the loop algorithm. In the worm algorithm,
two worms (or the head and tail of a worm) are created
randomly at nearby times in the (d +1)-dimensional
space-time. Then, the worms move randomly until they
meet again. The off-diagonal correlations like S
+
S
−
can also be calculated by using the worms [22.76,77].
22.3.6 Auxiliary Field Approach
The basic strategy of the auxiliary field quantum Monte
Carlo algorithm is the following: Auxiliary fields are in-
troduced in the path integral representation. Quantum
(fermionic) degrees of freedom are integrated exactly,
and the remaining degrees of freedom for (classical)
auxiliary fields are integrated by Monte Carlo tech-
niques. There is a powerful auxiliary field algorithm for
the Hubbard model [22.83–86]. We consider the Hub-
bard model defined by the following Hamiltonian
H ≡H
t
+H
U
, (22.60)
H
t
≡−t
i, j,σ
c
†
iσ
c
jσ
+c
†
jσ
c
iσ
, (22.61)
H
U
≡U
i
n
i↑
n
i
↓
, (22.62)
where c
iσ
and n
iσ
denote the annihilation operator and
the number operator with spin σ at site i, respectively.
The partition function defined in (22.49) can be decom-
posed as
Tr e
−βH
= lim
n→∞
Tr
e
−ΔτH
t
e
−ΔτH
U
n
, (22.63)
where Δτ =β/n. The exponential of the U-term can be
expressed in terms of auxiliary fields s
i
as [22.87]
e
−ΔτUn
i↑
n
i↓
=
1
2
s
i
=±1
e
2as
i
−
ΔτU
2
n
i↑
×e
−2as
i
−
ΔτU
2
n
i↓
, (22.64)
where cosh 2a = e
ΔτU
2
. Since the U-term is decom-
posed into up- and down-spin parts as
e
−ΔτH
U
=
1
2
N
s
s
1
,···,s
N
s
e
−ΔτH
↑
U
(s
1
,···,s
N
s
)
×e
−ΔτH
↓
U
(s
1
,···,s
N
s
)
, (22.65)
the partition function becomes
Z = lim
n→∞
1
2
N
s
n
{s}
Tr
σ
n
l=1
e
−ΔτH
σ
t
e
−ΔτH
σ
U
({s
l
})
= lim
n→∞
1
2
N
s
n
{s}
W
↑
({s})W
↓
({s}) , (22.66)
where {s}=s
i,l
(i = 1, ···, N
s
, l = 1, ···, n), {s
l
}=
s
i,l
(i =1, ···, N
s
), and N
s
denotes the number of sites.
It should be noted that in this expression the interac-
tions between up and down spins are removed in each
auxiliary-field configuration. This reduces the problem
to noninteracting fermions under local magnetic fields
produced by auxiliary fields. It is easy to solve the non-
interacting fermion problem. The effects of interactions
are taken into account through Monte Carlo samplings
for the auxiliary fields. By taking the trace over the
fermionic degrees of freedom, the weight W
σ
is ob-
tained as
W
σ
({s}) =det
I +
n
l=1
e
−ΔτH
σ
t
e
−ΔτH
σ
U
({s
l
})
.
(22.67)
Simulations are performed by updating auxiliary-field
configurations in the (d +1)-dimensional space-time.
The auxiliary-field Monte Carlo algorithm is also
used to investigate ground-state properties, replacing
the trace of the partition function in (22.49)bythe
expectation value of a trial state. This corresponds to
a kind of projection method.
22.3.7 Projector Monte Carlo Method
The basic principle of the projection method is to extract
the ground-state component by repeatedly applying the
Hamiltonian many times to a trial state. In the process
of multiplication of the Hamiltonian, configurations are
generated by Monte Carlo techniques [22.88,89]. Here,
as an example, we take the Monte Carlo power method
which is the simplest projection method.
Part E 22.3

Monte Carlo Simulation 22.3 Quantum Monte Carlo Method 1131
Let us suppose that a trial state (|ψ) has finite over-
lap with the ground state (|φ
0
), i. e.φ
0
|ψ= 0. Then,
physical quantities in the ground state are evaluated as
¯
O = lim
p→∞
¯
O
p
,
¯
O
p
≡
ψ|
ˆ
H
p
O
ˆ
H
p
|ψ
ψ|
ˆ
H
2p
|ψ
, (22.68)
where
ˆ
H ≡ H −C,andC is chosen such that |E
0
−
C|> |E
i
−C|. Here, E
0
is the ground-state energy, and
E
i
(i =1, 2, 3,...) the energy of ith excited state. In
Monte Carlo simulations, the trial state is expanded in
terms of the states which are used in Monte Carlo up-
dates such as site representation as |ψ=
i
a
i
|i. The
denominator of
¯
O
p
is expressed as
ψ|
ˆ
H
2p
|ψ=
i
0
,i
1
,···,i
2p
a
∗
i
2p
a
i
0
2p
j=1
i
j
|
ˆ
H|i
j−1
=
i
0
|a
i
0
|
2
path
(
WP
)
path
,
W =
a
i
0
a
i
2p
2p
j=1
i
j−1
|
ˆ
H|i
j
,
P =
2p
j=1
|a
i
j
|
2
|a
i
j−1
|
2
. (22.69)
Similarly, the numerator of
¯
O
p
can also be expressed
in terms of |i. Using Monte Carlo techniques, states
are generated according to the distribution determined
by |a
i
0
|
2
. From a configuration (|i
0
), we choose one of
the configurations which are reached by multiplying the
Hamiltonian with probability |a
i
1
|
2
/|a
i
0
|
2
. This proce-
dure is repeated 2p times to obtain the weight (W)of
apath.
¯
O
p
is calculated as the ratio of ψ|
ˆ
H
p
O
ˆ
H
p
|ψ
to ψ|
ˆ
H
2p
|ψ, which are approximately obtained as the
average of weights over all paths produced by Monte
Carlo samplings.
Monte Carlo updates for |i
0
are performed by the
algorithm of the variational Monte Carlo method. In this
sense, the Monte Carlo power method corresponds to
the extension of the variational Monte Carlo method to
make it possible to extract the ground-state component
from the variational trial state. As is well known, the
variational Monte Carlo method does not suffer from
the negative-sign problem. However, the Monte Carlo
power method does in general, because the weights W
can be negative. If we use the trial state that has the
same node structure with the ground state, the negative
sign problem does not appear. If negative weights can
be removed due to some special symmetry, the negative-
sign problem can also be avoided. Improved algorithms
of the Monte Carlo power method have been proposed
such as the power Lanczos method [22.90]whichmakes
the convergence faster by adopting the principle of the
Lanczos algorithm.
Here, we briefly review the ground-state version of
the auxiliary-field quantum Monte Carlo algorithm. As
a trial state, the state in the following form is used
|Φ=|Φ
↑
⊗|Φ
↓
,
|Φ
σ
=
M
j=1
N
s
i=1
Φ
σ
i, j
c
†
i,σ
|0, (22.70)
where M and N
s
are the numbers of up- (or down-)
spins and lattices, respectively. Using auxiliary fields,
the expectation value of the exponentials of the Hamil-
tonian by the trial state is expressed as
ρ
n
=Φ|
e
ΔτH
n
|Φ
=
{s
1
,···,s
n
}
W
↑
({s})W
↓
({s}) ,
W
σ
({s}) =det
t
Φ
σ
n
l=1
U
l
σ
({s
l
})K
l
Φ
σ
,
where U
l
σ
is a diagonal matrix whose diagonal
elements are 1/
√
2 exp(2as
i,l
σ −(ΔτU/2))/
√
2, and
K
l
=exp(−
¯
K). Here,
¯
K has non-zero matrix elements
−Δτt for (i, j) components, where i and j are the
nearest neighbors. Updates for the auxiliary fields are
performed in the same way as in the finite-temperature
algorithm.
The stochastic reconfiguration method [22.91–93]
is a projection method which is based on an exten-
sion [22.94,95] of the fixed-node approximation [22.96,
97]. In this method, configurations of walkers are re-
arranged so as not to increase negative weights under
the condition that expectation values of some operators
remain unchanged.
In principle, the ground state is obtained by pro-
jection methods through a large number of projection
steps, if trial states have finite overlap with the ground
state. However, special attention should be paid for the
choice of trial states in practice. If the symmetry of the
ground state is known, the trial state should be chosen
to have the same symmetry as the ground state. Then,
the simulations can be performed within the subspace
of this symmetry, and the convergence becomes faster.
Even though a trial state |φ
0
has a lower energy than
a state |φ
s
which has the same symmetry as the ground
state, the energy starting from |φ
s
can become lower
than that from |φ
0
at finite projection steps. The sym-
Part E 22.3

1132 Part E Modeling and Simulation Methods
metries of the ground state that need to be taken into
account commonly are, for example, the total spin S =0
and total momentum K = 0. Such a trial state may be
better than ordered states as an initial state of projection
methods.
22.3.8 Negative-Sign Problem
In quantum Monte Carlo simulations, partial Boltzmann
weights may be negative. Since the Markov process
cannot be defined for negative weights, simulations
are based on the absolute values of weights. The sta-
tistical average of a physical quantity is obtained by
dividing the average of physical quantity with signs
of weights by the average of signs. Generally, at low
temperatures or in large systems, the average of signs
becomes exponentially small, and its statistical error be-
comes exponentially large. This difficulty is called the
negative-sign problem.
Here, we show a simple example that exhibits the
negative-sign problem. We consider the Heisenberg
model defined by (22.52) in a three-site cluster with
the Trotter number three. There are three types of
world-line configurations as shown in Fig. 22.9.Other
world-line configurations can be obtained by inversion
of spin directions or translations.
The weights of these configurations are
a) w
↑↑
↑↑
3
,
(a)
1
(1)
3
2
1
2 3 (1)1
(1)
3
2
1
2 3 (1)
(c)
1
(1)
3
2
1
2 3 (1)
(b)
Fig. 22.9a–c World-line configurations for a three-site
system
b) w
↓↑
↓↑
w
↑↑
↑↑
2
and
c) w
↑↓
↓↑
3
,
where local weights are defined in Table 22.1.Since
w
↑↓
↓↑
is negative, the weight of (c) is negative. If
we define the probability as in (22.53), the probability
of (c) from (b) (or (b) from (c)) becomes negative. Thus,
we decouple the weight W into the positive weight W
and the sign S as W = W
× S. The probability is then
redefined as P = W
new
/(W
new
+W
old
). The average of
physical quantity Q is obtained as
Q=
A
W(A)Q(A)
A
W(A)
=
A
W
(A)S(A)Q(A)
A
W
(A)S(A)
=
A
W
(A)S(A)Q(A)
/
A
W
(A)
A
W
(A)S(A)
/
A
W
(A)
=
SQ
S
, (22.71)
where
denotes the average with respect to W
.
When the number of negative weights is as large as that
of positive weights, S
becomes almost zero. Then, the
statistical error becomes large. The negative sign prob-
lem is generally severe in the low-temperature regime.
Spin models without frustration do not suffer from
the negative-sign problem, because all the weights
can be chosen as positive by a gauge transforma-
tion. The Hubbard models on bipartite lattices with
attractive interactions (U < 0) or those with repulsive
interactions (U > 0) at half-filling do not have nega-
tive weights. One-dimensional electron systems with
nearest-neighbor hopping also do not suffer from the
negative-sign problem in general.
Even with frustrations or strong correlations, some
models can be simulated without negative-sign prob-
lems by using special algorithms. For some frustrated
Heisenberg chains, quantum Monte Carlo simulations
can be performed free of negative-sign problems by
the algorithm shown in [22.98]. In this algorithm, the
representation basis is changed from the conventional
S
z
-basis to the dimer basis. Using this dimer basis,
the system is described as a single chain where dimer
units are connected with a single effective coupling. The
Part E 22.3

Monte Carlo Simulation 22.4 Bicritical Phenomena in O(5) Model 1133
suppression of negative weights can be proved by a non-
local unitary transformation with appropriate coupling
constants.
Another algorithm which does not suffer from the
negative-sign problem for strongly-correlated electron
systems is shown in [22.99, 100]. This algorithm is
based on a cluster algorithm and called the meron-
cluster algorithm. The model considered here is the
fermionic version of the spin-1/2 Heisenberg model
without chemical potentials. For fermionic systems,
there are two types of clusters, one changing their
signs by a flip, and the other not. The former is called
meron-clusters. Only the configurations without meron-
clusters contribute to the average of the sign Sign,
since in the cluster algorithm without magnetic fields
(which correspond to chemical potentials for fermionic
systems), clusters flip independently with probability
1/2: Configurations with meron-clusters cancel signs
by a flip ((+1−1)/2 =0). For the calculation of suscep-
tibilities χ =O
2
Sign/Sign, only the configurations
with zero or two meron-clusters contribute. Thus, up-
dating configurations with the restriction that there are
at most two meron-clusters, susceptibilities can be cal-
culated with sufficient statistics.
22.3.9 Other Exact Methods
There are some methods which give exact results for
large quantum systems in principle other than quan-
tum Monte Carlo methods. One is the high-temperature
expansion method [22.101, 102]. In this method, the
partition function is expanded in powers of the in-
verse temperature. Thus, this method gives exact results
in the high-temperature limit and is applicable to any
models in the thermodynamic limit. Properties in the
low-temperature regime are investigated by extrapolat-
ing data using the Padé approximation.
The density-matrix renormalization group (DMRG)
method also gives accurate results in large-size sys-
tems [22.103, 104]. In this method, the ground state
is approximated by eigen states of the density matrix
with large weights. The states are updated by adding or
readjusting local sites. Hence, this method is effective
for one-dimensional systems with open boundary con-
ditions. This method has been extended to investigate
finite-temperature properties [22.105–109].
In order to investigate electron systems without
suffering from the negative-sign problem, the path-
integral renormalization group (PIRG) method has
been developed [22.110–112]. In this method, the
ground state is approximated by a linear combina-
tion of nonorthogonal single-particle states in the form
of (22.70). The states are selected so as to minimize
the energy. Single-particle trial states are generated
in the same way as in the auxiliary-field quantum
Monte Carlo method. This method is applicable to the
Hubbard models in any dimensions even with frustra-
tions [22.113–115].
22.4 Bicritical Phenomena in O(5) Model
Several applications of the Monte Carlo techniques are
reviewed in the remaining part of this chapter. The first
one is for a classical O(5) model. The competition be-
tween antiferromagnetism (AF) and superconductivity
(SC) is observed in high-T
c
superconductors and sev-
eral others including organic ones, where the effects
of strong correlations among electrons are important.
This feature has led to the SO(5) theory, where the
U(1) symmetry of SC and SU(2) symmetry of AF is
unified to a group of SO(5) [22.116, 117]. The SO(5)
symmetry is achieved through the competition between
the two orders at a bicritical point [22.118, 119]in
the phase diagram. In general, however, the symme-
try of a fixed point, or even its existence, depends on
the dimensionality, the number of degrees of freedom,
as well as biquadratic perturbations [22.120, 121]. In
literature [22.122], the following picture for the stabil-
ity of the multicritical point for 5 spin-components in
three dimensions is provided by the ε expansions of
the renormalization group (RG) theory: for positively
large, biquadratic AF-SC couplings, the normal(N)-AF
and N-SC transitions switch from second to first order
before the two critical lines touch because of ther-
mal fluctuations, resulting in two tricritical points and
a triple point in the phase diagram; the stable fixed point
should be a decoupled, tetracritical point characterized
by a negative biquadratic AF-SC coupling.
Our Monte Carlo (MC) simulations on the O(5)
Hamiltonian in three dimensions [22.123, 124] indicate
however that the bicritical point is stable as far as the bi-
quadratic coupling is nonnegative, and that for negative
biquadratic couplings the biconical, tetracritical point
takes the place, in contrast to the RG results. We have
formulated a scaling theory on the order parameters,
which provides a powerful tool for estimation of the bi-
critical point and the bicritical and crossover exponents.
Part E 22.4
1134 Part E Modeling and Simulation Methods
22.4.1 Hamiltonian
The Hamiltonian is given by [22.123]
H =−
i, j
J
AF
ij
s
i
·s
j
−
i, j
J
SC
ij
t
i
·t
j
+g
i
s
2
i
+w
i
s
2
i
t
2
i
, (22.72)
on the simple cubic lattice. The couplings are lim-
ited to nearest neighbors. The vector s(t) of three(two)
components is for the local AF(SC) order parameter,
and s
2
i
+t
2
i
= 1. The Hamiltonian (22.72)isO(3)and
O(2) symmetric with respect to the rotations in the two
subspaces for s and t, respectively. The symmetries
are broken spontaneously when temperature is below
the corresponding critical points. The system enjoys
a higher O(5) symmetry for J
AF
ij
= J
SC
ij
and g =w =0,
while anisotropy in coupling constants breaks the O(5)
symmetry. There are two other fields which break the
symmetry: g field associated with the chemical poten-
tial of electrons and w field with the quantum effects
of Gutzwiller projection of double occupancy of elec-
trons [22.125,126]. Higher-order terms are known to be
irrelevant to critical phenomena and thus are omitted in
our study.
In a typical MC simulation process, we generate
a random configuration of superspins at a sufficiently
high temperature, and then cool down the system gradu-
ally. The conventional Metropolis algorithm is adopted,
with 50 000 MC steps for equilibration and 100 000 MC
steps for statistics on each superspin at a given tempera-
ture. The system size for data shown here is L
3
= 40
3
with periodic boundary conditions. We have simulated
up to L
3
=80
3
and confirmed that finite-size effects do
not change our results.
22.4.2 Phase Diagram
For the long-range order parameters of SC, we adopt the
helicity modulus defined by
Υ ≡ lim
θ→0
F(θ)−F(0)
(θ/L)
2
S
, (22.73)
where the free energy F(θ) is for the system under
a twist, for example, along x direction, ϕ → ϕ +θ ×
(1 −2x/L) with S = L
2
for the cross section. For the
long-range order parameter of AF, the staggered mag-
netization is used
m =
1
N
i
s
i
2
.
(22.74)
1
0.8
0.6
0.4
0.2
0
g = 0.01 J
g = 0.05 J
g = 0.10 J
g = 0.20 J
g = 0.50 J
g = 1.00 J
g = 2.00 J
Y (J)
T (J/k
B
)
0 0.3 0.6 0.9 1.2 1.5
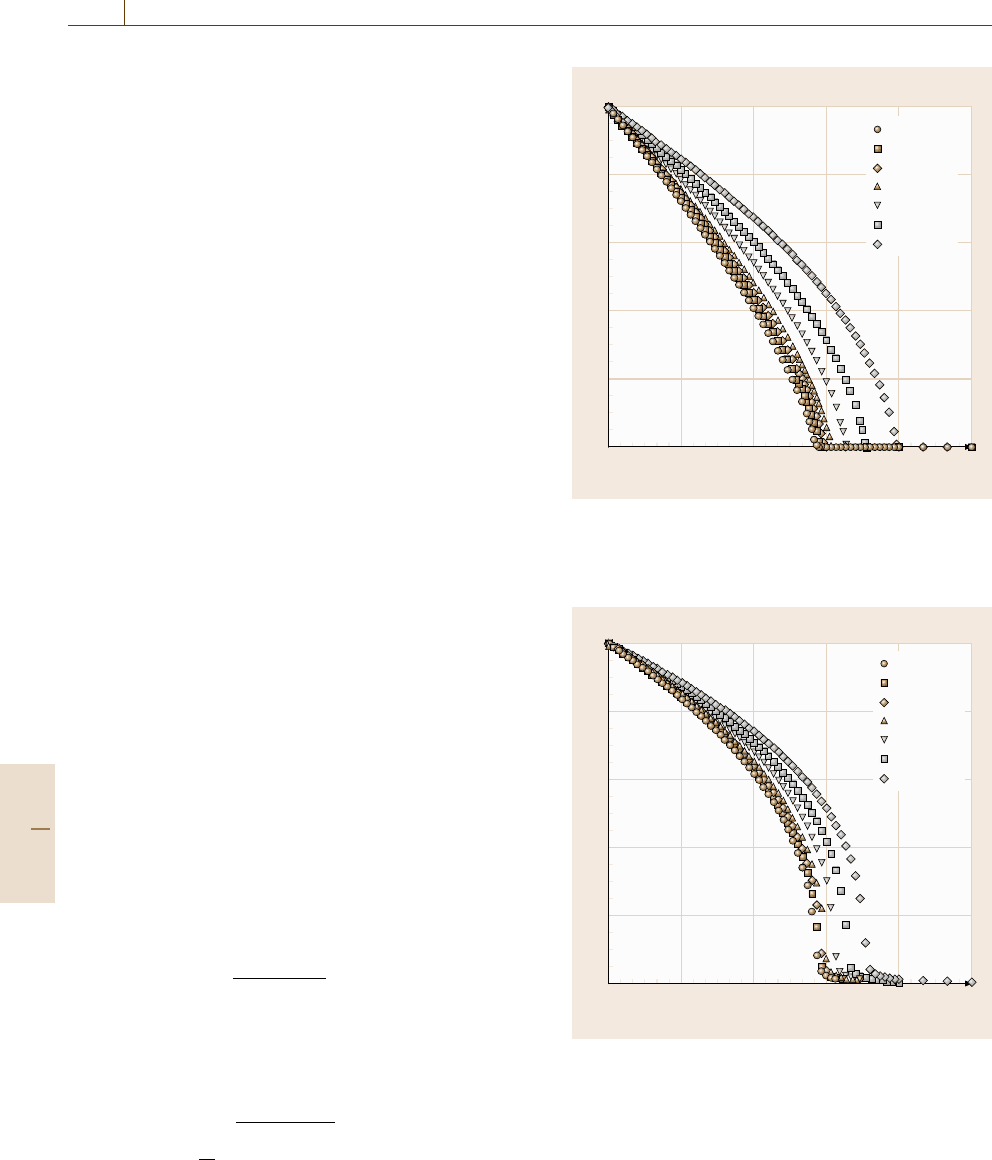
Fig. 22.10 Temperature and g dependence of the helicity
modulus for isotropic couplings and w =0 (after [22.123,
124])
g = 0.01 J
g = 0.05 J
g = 0.10 J
g = 0.20 J
g = 0.50 J
g = 1.00 J
g = 2.00 J
m
T (J/k
B
)
0 0.3 0.6 0.9 1.2 1.5
1
0.8
0.6
0.4
0.2
0
Fig. 22.11 Temperature and g dependence of the stag-
gered magnetization for isotropic couplings and w = 0
(after [22.123,124])
First we show the simulation results for the simplest
case of J
AF
ij
= J
SC
ij
(= J)andw = 0 in Figs. 22.10 and
Part E 22.4
Monte Carlo Simulation 22.4 Bicritical Phenomena in O(5) Model 1135
b
AF
–2 –1 0 1 2
SC
1.2
1.1
1
0.9
0.8
0.7
T
c
T
N
T
(J/k
B
)
g
(J)
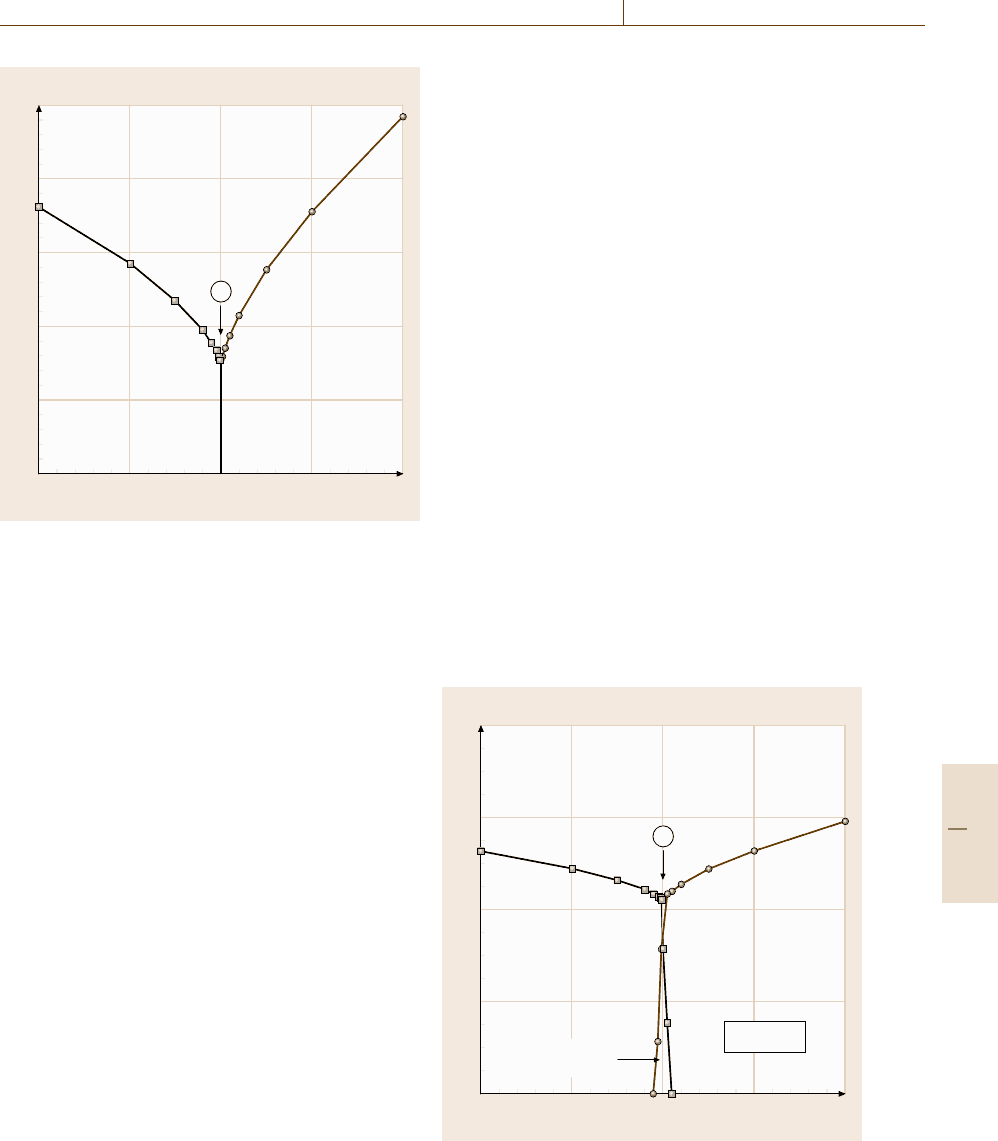
Fig. 22.12 g-T phase diagram with a bicritical point for
isotropic couplings and w =0 (after [22.123,124])
22.11. The helicity modulus (staggared magnetization)
is zero for g < 0(g > 0).
The phase diagram thus obtained is depicted
in Fig. 22.12. The bicritical point is located at
[g
b
, T
b
]=[0, 0.845J/k
B
], at which the two critical lines
merge tangentially. We shall address the crossover phe-
nomenon in Fig. 22.12 as g → 0 later.
We have also turned on the anisotropy in the cou-
pling constants: J
SC
c
= J/10, namely the SC coupling
along the c crystalline axis is 1/10 of other coupling
constants, while keeping w = 0. The bicritical point is
achieved at [g
b
, T
b
]=[1.18J, 0.67J/k
B
] [22.127]. It is
interesting to observe that the O(5) symmetry broken
by the coupling anisotropy is recovered by tuning the
g field to the common tangent of the two critical lines
starting from the bicritical point.
Next, we check the stability of the bicritical point
upon introducing a positive w field. It is revealed
that the Gutzwiller projection out of the double occu-
pancy of electrons in high-T
c
cuprates should result in
a positive biquadratic AF-SC coupling [22.125, 126].
Without losing generality, let us set w =0.1J in Hamil-
tonian (22.72). For g ≥ 0.012J and g ≤ 0.010J we
observe long-range SC and AF orders, respectively. At
g =0.011J either AF or SC is realized depending on
the initial random configuration and cooling process,
same as at g = g
b
=0forw =0. No homogeneous co-
existence between AF and SC can be observed, and
all the phase transitions upon temperature reduction are
second order, and thus there is no fluctuation-induced
first-order transition suggested by the RG ε expansions.
The phase diagram for w = 0.1J is the same as that
in Fig. 22.12 for w =0 except that the bicritical point
shifts to g
b
=0.011J [22.123].
We have increased the w field to w =0.5J suppos-
ing that it should result in stronger first-order N-AF and
N-SC phase transitions in wider regimes, if any. Sys-
tems have also been enlarged up to L
3
=80
3
in order to
check possible finite-size effects. All we have observed
are second-order N-AF and N-SC transition and a stable
bicritical point.
For the negative biquadratic coupling w =−0.1J,
we observe a biconical, tetracritical point at g
t
=
−0.011J (of the same absolute value of g
b
for
w = 0.1J) as shown in Fig. 22.13. There is a region in
the phase diagram where AF and SC coexist homoge-
neously.
22.4.3 Scaling Theory
For positively large enough g field, there is a suffi-
ciently large temperature region above the SC critical
line where AF fluctuations are irrelevant to the criti-
cal phenomenon. This critical region characterizing the
SC
w = –0.1 J
AF & SC
coexistence
t
AF
–2 –1 0 1 2
1.6
1.2
0.8
0.4
0
T
c
T
N
T
(J/k
B
)
g
(J)
Fig. 22.13 g-T phase diagram with a bicritical point for
isotropic couplings and w =−0.1J (after [22.123, 124])
Part E 22.4
1136 Part E Modeling and Simulation Methods
η
v
5
/
φ
η = g/g' = 0.5
0.83 0.84 0.85 0.86
0.8
0.7
0.6
0.5
T
b
Y(T; g)/Y(T; g')
g = 0.05 J; g' = 0.10 J
g = 0.10 J; g' = 0.20 J
T
(J/k
B
)
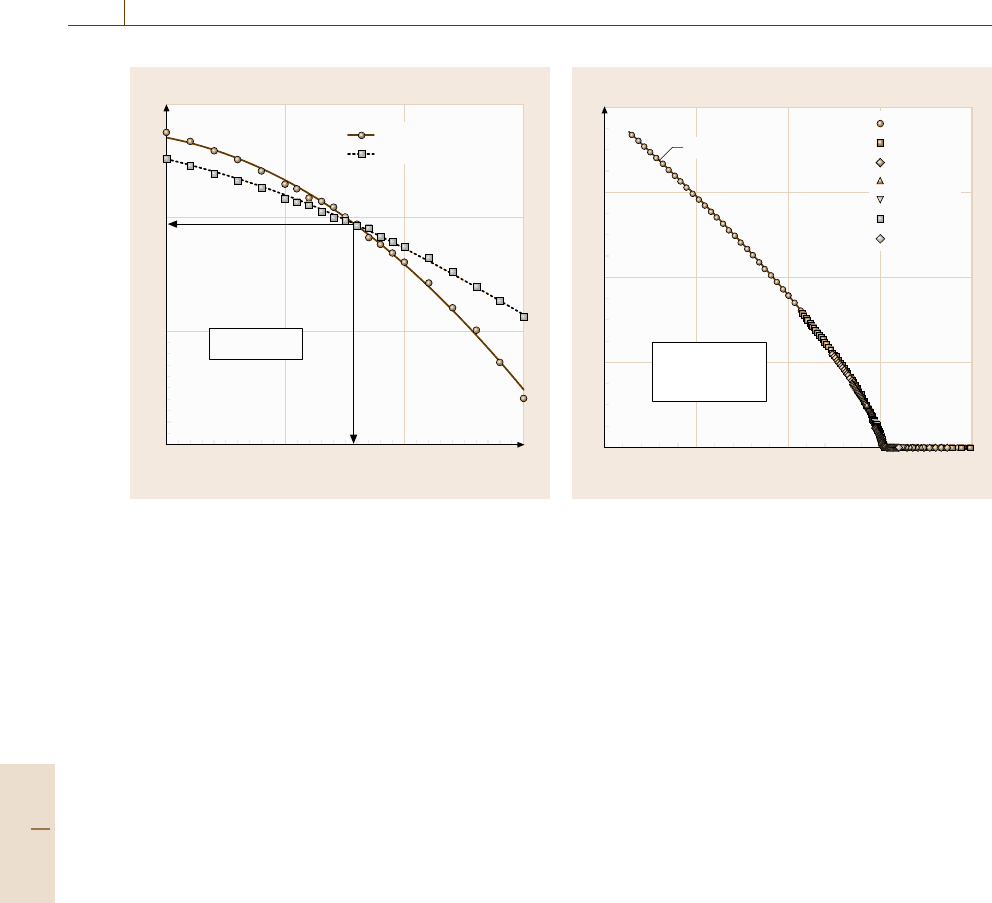
Fig. 22.14 Scaling plot for estimation on the bicritical
point and the ratio ν
5
/φ according to (22.79) (after [22.123,
124])
O(2) symmetry breaking is, however, shrinking as g is
reduced. This can be read from the temperature depen-
dence of the helicity modulus in Fig. 22.10, and can be
understood easily, at least qualitatively, since in Hamil-
tonian (22.72) thermal fluctuations associated with the
O(5) symmetry become more important as g decreases.
Similar behaviors are observed for the Néel order pa-
rameter for g < 0.
In order to analyze the crossover phenomenon quan-
titatively, we develop the scaling theory for order
parameters below the critical lines (see [22.128]forthe
scaling theory for the response functions above the crit-
ical lines)
Υ (T;g) Ag
ν
5
/φ
× f
(T/T
b
−1)/g
1/φ
, (22.75)
with ν
5
for the bicritical singularity of n = 5andφ the
crossover exponent. For simplicity, we consider here the
case of g
b
=0, noticing that extension to cases g
b
=0is
straightforward. The scaling function f (x) should have
the following properties
f (x)
(−x)
ν
5
, as x →−∞;
(B
2
−x)
ν
2
, as x → B
2
,
(22.76)
with B
2
defined by
B
2
g
1/φ
= T
c
(g)/T
b
−1 , (22.77)
v
5
= 0.728
φ = 1.387
T
b
= 0.8458 J/k
B
–30 –20 –10 10
12
9
6
3
0
Y(T; g)/g
v
5
/
φ
f(x) = (–x)
v
5
(T/T
b
–1)/g
1/φ
g = 0.01 J
g = 0.05 J
g = 0.10 J
g = 0.20 J
g = 0.50 J
g = 1.00 J
g = 2.00 J
Fig. 22.15 Scaling plot for the data on helicity modulus in
Fig. 22.10 according to (22.75) (after [22.123,124])
which describes the SC critical line. With the properties
(22.76), we can arrive at
Υ (T;g)
A ×(1−T/T
b
)
ν
5
, for g =0;
A ×(1−T/T
c
(g))
ν
2
, for g > 0.
(22.78)
This formulation of the bicritical scaling theory permits
us to evaluate the bicritical and crossover exponents as
well as the bicritical point in high precisions from the
MC simulation results.
From the scaling ansatz (22.75), one should have
Υ (T
b
;ηg)/Υ (T
b
;g) =η
ν
5
/φ
. (22.79)
In order to fully utilize this relation, we plot in
Fig. 22.14 the g and temperature dependence of
Υ (T
b
;ηg)/Υ (T
b
;g)forη =1/2. The two curves should
cross at the point [T
b
,η
ν
5
/φ
] according to (22.79).
Therefore, we estimate T
b
0.8458 ±0.0005J/k
B
and
ν
5
/φ 0.525 ±0.002. Each point in Fig. 22.14 is ob-
tained by 3 million MC steps on each superspin.
The crossover exponent φ can be evaluated from
the slope κ[η;g] of Υ (T;ηg)/Υ (T ;g) with respect to
temperature at the bicritical point T
b
in Fig. 22.14
φ = ln
g
2
/g
1
/ ln
κ[η;g
1
]/κ[η;g
2
]
. (22.80)
In this way, we have φ = 1.387 ±0.030 with the error
bar estimated from those of the slopes. Finally, we arrive
at ν
5
=0.728 ±0.018.
Part E 22.4

Monte Carlo Simulation 22.5 Superconductivity Vortex State 1137
g = 0.01 J
g = 0.05 J
g = 0.10 J
g = 0.20 J
g = 0.50 J
g = 1.00 J
g = 2.00 J
v
5
= 0.728
φ = 1.387
T
b
= 0.8458 J/k
B
v
2
= 0.666
–3 –2 –1 0 1/4 1
2
1.5
1
0.5
0
Y(T; g)/g
v
5
/
φ
f(x) = (1/4 –x)
v
2
(T/T
b
–1)/g
1/φ
Fig. 22.16 Zoom in of Fig. 22.15 around the origin (after
[22.123,124])
With the estimates on the bicritical point and the bi-
critical, crossover exponents, we can plot the data in
Fig. 22.10 in the scaled way described in (22.75). The
result is depicted in Figs. 22.15 and 22.16, where we
have A 1.0andB
2
1/4. The singularity at x = B
2
can be fitted very well by the critical exponent for
the pure XY model of O(2) symmetry ν
2
0.67 as in
(22.78). To the best of our knowledge, the scaling the-
ory for bicritical phenomena is verified in such a precise
way for the first time.
The scaling analysis for the AF order parameters for
g < 0 can be performed in the same way. Beside the
critical exponents we have obtained the coefficient B
3
1/6 which describes the critical line of AF order
B
3
(−g)
1/φ
= T
N
(g)/T
b
−1 . (22.81)
The ratio B
2
/B
3
=3/2 is given by the inverse ratio of
the two degrees of freedom and should be a universal
constant for the competition between two orders of two
and three components such as in the high-T
c
supercon-
ductivity.
Since the helicity modulus is related to the London
penetration depth Υ ∼1/λ
2
, the scaling theory is ex-
pected to be useful for analyzing experimental results.
Another interesting issue for the AF-SC competition
is the magnetic-field effect. When we apply an exter-
nal magnetic field, the long-range SC order is achieved
in the form of the Abrikosov flux-line lattice. The N-
SC transition becomes first order accompanied by the
melting of flux-line lattice. Because the strong thermal
fluctuations in the SC sector, the N-AF transition be-
comes first order nearby the AF-SC phase boundary.
There is a tricritical point on the N-AF phase boundary
where the N-AF transition is switched back to second
order [22.129].
22.5 Superconductivity Vortex State
Superconductivity is one of the most fascinating phys-
ical phenomena, because of its perfect conductance
of electricity. Its prominent character is however the
peculiar magnetic property, namely the diamagnetism
known as the Meissner effect. A deeply related phe-
nomenon is the quantization of magnetic flux by
superconductivity. There are two kinds of supercon-
ductors, type I and II. The superconductivity in type
I samples is broken discontinuously by increasing
magnetic field to a critical value. For type II su-
perconductors, according to the mean-field theory by
Abrikosov [22.130, 131], who shared the Nobel Prize
of Physics in 2003 with Ginzburg and Leggett, there
exist two critical magnetic fields: at the lower critical
field H
c
1
quantized fluxes start to penetrate into the
sample and form a triangular lattice of flux lines; at
the upper critical field H
c
2
superconductivity is sup-
pressed because of the overlapping of flux cores. Both
the translation and rotation symmetry associated with
the spatial distribution of flux lines and the local U(1)
gauge symmetry are broken at the upper critical field
H
c
2
. In the mean-field theory, this phase transition is
second order.
Although the theory by Abrikosov is ground
breaking, thermal fluctuations are not treated suffi-
ciently. The discovery of high-T
c
superconductivity in
cuprates makes the thermal-fluctuation regime acces-
sible. A first-order melting of the flux-line lattice was
proposed based on transport measurements, in which
resistance drops discontinuously. Later on, experiments
on thermodynamic quantities, such as magnetization
and the specific heat, revealed clearly the first-order
nature of the phase transition. For review articles,
see [22.132–134].
A theoretical understanding toward the phase tran-
sition in vortex states beyond mean-field theory is not
Part E 22.5
