Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing
Подождите немного. Документ загружается.

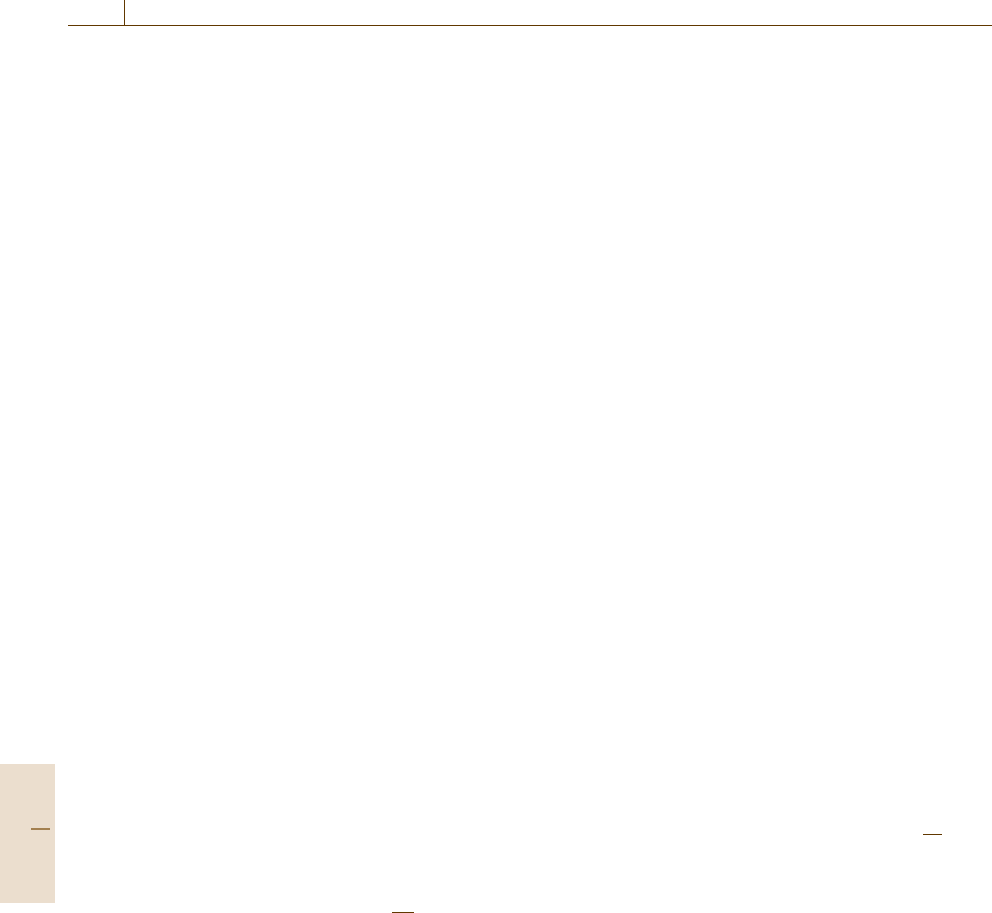
1138 Part E Modeling and Simulation Methods
easy. It is shown by the ε expansions of renormaliza-
tion group (RG) that the superconductivity to normal
phase transition should be first order,uptothelow-
est order of ε [22.135]. This result is natural since the
melting of the flux-line lattice is understood to be simi-
lar to most other melting phenomena in reality (d = 3).
However, the upper critical dimension for the supercon-
ductivity vortex state is d
u
=6, above which mean-field
theory is correct, since thermal fluctuations in the two
dimensions perpendicular to the magnetic field are cut
off by the vortex spacing and thus cannot contribute
to the long-range order, noticing d
u
= 4 for supercon-
ductivity without magnetic field. The treatment on RG
flows is therefore quite hard using quantities only to the
lowest order of ε = d
u
−d = 3.Asamatteroffact,the
conclusion on the first-order melting transition of vortex
lattice from RG was challenged by others.
22.5.1 Model Hamiltonian
This situation motivated many computer simulation
works. As the melting temperature is much lower than
T
c
2
(B), where the Meissner effect sets on, it is a rea-
sonable approximation to neglect fluctuations in the
amplitude of the complex order parameter when the
melting transition is concerned. In addition, the high-
T
c
superconductors are extremely type-II, in which the
penetration length of magnetic field is much larger than
the correlation length. This permits one to take the
magnetic induction uniform and equal to the applied
magnetic field.
With these two approximations we can de-
rive the following three-dimensional frustrated XY
model [22.136, 137] from the Ginzburg–Landau (GL)
Lawrence–Doniach (LD) free-energy functional for lay-
ered superconductors [22.138,139]
H =−
i, j
J
ij
cos
⎛
⎜
⎝
ϕ
i
−ϕ
j
−
2π
φ
0
j
i
A· d r
⎞
⎟
⎠
.
(22.82)
Namely, the main effects of thermal fluctuations come
from the phase degrees of freedom of superconductivity
order parameter, which are defined on the simple cu-
bic lattice in simulation. The couplings are limited to
nearest neighbors and J
ij
= J with J = φ
2
0
d/16π
3
λ
2
ab
for links ij parallel to the superconducting layer while
J
ij
= J/Γ
2
for the perpendicular. The lattice constant
along the c direction is the separation between neigh-
boring CuO
2
layers d, while the lattice constant in
the ab planes l
ab
can be taken in a range satisfying
ξ
ab
l
ab
λ
ab
. Then the anisotropy parameter should
be given by the relation Γ l
ab
= γ d if one wants to
simulate a superconductor with anisotropy parameter
γ = λ
c
/λ
ab
.
For magnetic fields parallel to the c axis, one can
set A
z
=0. The strength of the magnetic field is given
in a dimensionless way f ≡ Bl
2
ab
/φ
0
. Vortices are fig-
ured out, including vorticity n, by counting the gauge
invariant phase differences around any plaquette
i, j
[ϕ
i
−ϕ
j
− A
ij
]=2π(n − f ) . (22.83)
In the ground state, the areal density of vortices should
be equal to f .
In the above model, we assume a finite amplitude
of local superconductivity order parameter on each site,
which gives the coupling strength. At high tempera-
tures, the phases fluctuate significantly and thus a coarse
grain to any length scales larger than that given initially
in the model will result in a vanishing amplitude of su-
perconductivity order parameter. As for the long-range
order of superconductivity, one needs to investigate
the coherence of the phase degrees of freedom in the
present system. The helicity modulus proportional to
the rigidity of the system under an imposed phase twist
as in (22.75) should be taken as the true long-range
superconductivity order parameter.
22.5.2 First Order Melting
Here we present some of our results published
in [22.140–142], with simulation techniques devel-
oped partially in early studies [22.143]. Similar results
are reported by other groups [22.144–146]. For the
convenience of simulation, we take Γ =
√
10 when
modeling the moderately anisotropic high-T
c
supercon-
ductor YBa
2
Cu
3
O
7−δ
of γ = 8. The magnetic field is
f = 1/25. The system size is L
ab
× L
ab
× L
c
=50× 50×
40, where N
v
= 100 vortices induced by the external
magnetic field are contained in each ab plane. Periodic
boundary conditions (PBCs) are set in all the directions.
The conventional Metropolis algorithm is adopted. The
number of MC sweeps at each temperature is 50 000
for equilibration and 100 000 for sampling. Around the
transition temperature, we have simulated up to several
million MC sweeps.
The Specific Heat
In Fig. 22.17 we display the temperature dependence of
the specific heat per vortex line per length d evaluated
Part E 22.5
Monte Carlo Simulation 22.5 Superconductivity Vortex State 1139
C (k
B
per vortex)
T (J/k
B
)
0 0.2 0.4 0.80.6 1.21 1.4 1.6
26
24
22
20
18
16
14
12
Fig. 22.17 Temperature dependence of the specific heat per
vortex line per length d
via the fluctuation-dissipation theorem
C =
H
2
−H
2
/k
B
T
2
. (22.84)
A sharp spike is observed in the specific heat around the
temperature T
m
0.567J/k
B
. Quantitatively, the spe-
cific heat is C
+
18.5k
B
just above T
m
, C
max
23k
B
right on T
m
,andC
−
17.5k
B
just below T
m
in a narrow
regime of temperature.
Figure 22.18 displays the variation of the internal
energy around the transition temperature T
m
. A kink-
like anomaly takes place, and from the two straight
lines in Fig. 22.18 the latent heat is estimated as
Q 0.07k
B
T
m
per flux per layer. The data on the spe-
cific heat and the latent heat indicate very clearly that
a first-order phase transition occurs at T
m
.
According to the finite-size scaling theory for a first-
order phase transition [22.1], one has
C
max
=
Q
2
4k
B
T
2
m
L
2
ab
L
c
f +
C
+
+C
−
2
, (22.85)
ΔT =
2k
B
T
2
m
QL
2
ab
L
c
f
, (22.86)
providing that the system is already large enough such
that the estimate of the latent heat in the way de-
scribed in Fig. 22.18 is accurate enough. It has been
checked that our data satisfy these two relations very
e (J per vortex)
T (J/k
B
)
0.555 0.5650.56
Q
0.5750.57 0.58 0.585
–38.9
–39
–39.1
–39.2
–39.3
–39.4
–39.5
Fig. 22.18 Temperature dependence of the internal energy
per vortex line per length d
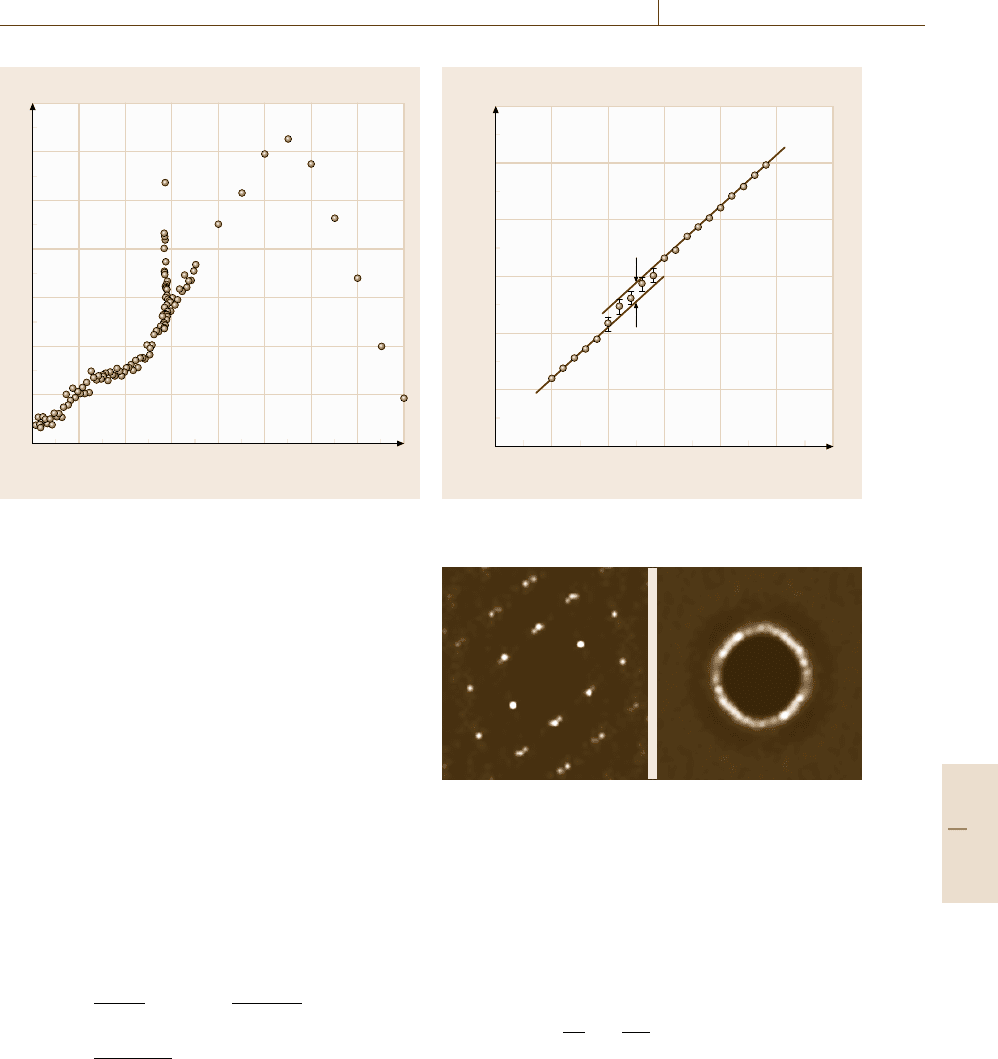
a) b)
Fig. 22.19a,b Structure factors for vortex lattice at low
temperature (a) and vortex liquid at high temperatures (b)
well. Therefore, we can say that the present simulation
results are statistically and thermodynamically correct.
Structure Factor
The correlation functions of vortices can be described
by a structure factor defined by
S(q
ab
, z) =
1
N
v
∞
−∞
dq
c
2π
e
iq
c
z
n(q)n(−q), (22.87)
where n(q) =
r
n(r)exp(−iq ·r)andn(r)isthevor-
ticity in the c direction (i. e., along the magnetic field)
at position r. Two typical structure factors S(q
ab
, z = 0)
for the in-plane correlation functions of vortices are de-
picted in Fig. 22.19. It becomes clear that the first-order
Part E 22.5
1140 Part E Modeling and Simulation Methods
phase transition is a melting transition of the vortex lat-
tice of hexagonal symmetry into the isotropic vortex
liquid.
Helicity Modulus
The temperature dependence of the helicity modulus
along the c axis
Υ
c
=
1
L
2
ab
L
c
i, j
J
ij
cos(ϕ
i
−ϕ
j
)(
ˆ
e
ij
·
ˆ
c)
2
−
1
k
B
TL
2
ab
L
c
!
i, j
J
ij
sin(ϕ
i
−ϕ
j
)(
ˆ
e
ij
·
ˆ
c)
"
2
+
1
k
B
TL
2
ab
L
c
i, j
J
ij
sin(ϕ
i
−ϕ
j
)(
ˆ
e
ij
·
ˆ
c)
2
,
(22.88)
is presented in Fig. 22.20. It increases from zero to
a finite value Υ
c
(T
m
) 0.6J/Γ
2
in a narrow tempera-
ture region around T
m
as the system is cooled down.
Therefore, the phase transition at T
m
is the normal to
superconducting phase transition. The sharp onset of Υ
c
is another indication of first-order transition. The helic-
ity modulus in the ab plane remains zero even below
the transition temperature T
m
. Therefore, the system is
superconducting only along the c axis even below T
m
.
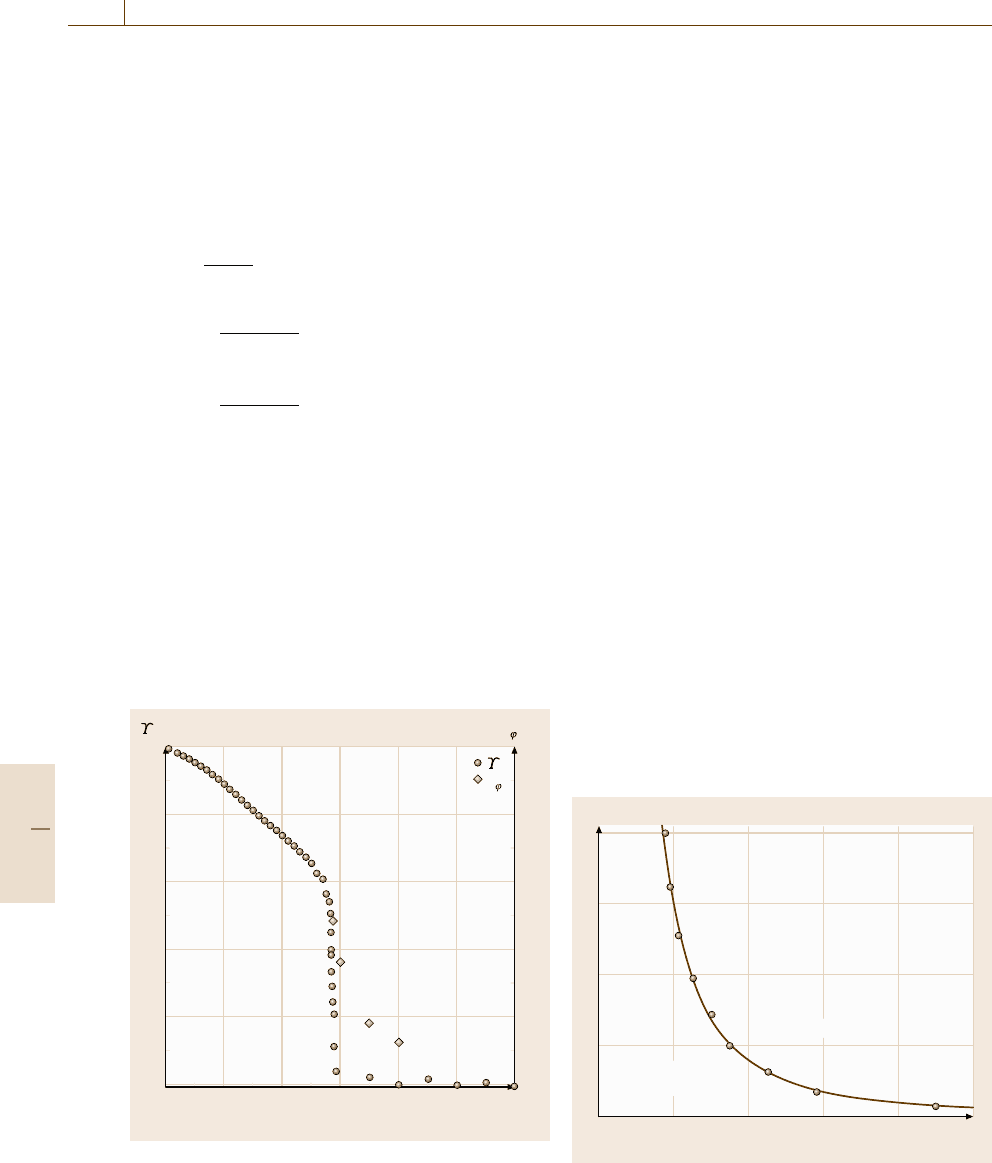
ξ (d)
T (J/k
B
)
0 0.2 0.4 0.80.6 1 1.2
1
0.8
0.6
0.4
0.2
0
20
16
12
8
4
0
ξ
c
c
(J/Γ
2
)
Fig. 22.20 Temperature dependence of the helicity modu-
lus and the correlation length
The correlation length of phase variables along
the c direction increases with cooling and reaches to
ξ
ϕ,c
10d at the melting temperature. We notice that
our system size is L
c
=40 in units of d, and is therefore
sufficient for simulating the true phase transition of the
vortex system of the given parameters. If a smaller sys-
tem of L
c
≤20 was taken, the system would behave as
if a long-range SC order had established at a tempera-
ture above the melting point, where the structure factor
evolves from that of the liquid into the lattice. Then one
would be led to two phase transitions, instead of the true
single one.
Phase Diagram
By tuning the magnetic field, or equivalently the
anisotropy parameter, we have mapped out the B-T
phase diagram of the pancake vortices as shown in
Fig. 22.21. The decreasing melting temperature with in-
creasing magnetic field is consistent with the Clausius–
Clapeyron relation
ΔB =−4πΔs/(dB
m
/dT ) , (22.89)
where Δs is the entropy jump of unit volume. Taking
into account the temperature dependence of the penetra-
tion depth, and thus that of the coupling strength in our
model, we can [22.142] compare our numerical results
with experiments. The agreement is quite satisfactory as
in Table 22.5.
The hump in the specific heat at T
v
1.1J/k
B
is produced by a huge number of thermal excita-
tions of vortices in the form of closed loops. Even
local superconductivity order parameters cannot sur-
B (φ
0
/(γd)
2
)
T (J/k
B
)
0.2 0.4
Flux-line
lattice
Vortex liquid
0.80.6 10
4
3
2
1
0
Fig. 22.21 B-T phase diagram (after [22.142])
Part E 22.5
Monte Carlo Simulation 22.5 Superconductivity Vortex State 1141
Table 22.5 Comparison between our simulation results
and experimental observations for YBa
2
Cu
3
O
7−δ
. ΔS de-
notes the entropy jump per flux line per length d
B =8Tesla T
m
[K] ΔS[k
B
] ΔB [G]
Simulation 81 0.55 0.19
Experiment 79 0.4 0.25
vive at any scale larger than the grid, which indicates
T
v
= T
c
2
. Therefore, treating thermal fluctuations suc-
cessfully makes the mean-field phase transition at H
c
2
a crossover.
22.5.3 Continuous Melting: B||ab Plane
When the external magnetic field is applied parallel
to the CuO
2
layers of a high-T
c
superconductor, mag-
netic induction tends to penetrate the sample through
the positions where superconductivity concentration is
lower, namely the so-called block layers. Because of
the Josephson couplings, magnetic induction is still
quantized, the so-called interlayer Josephson vortices.
A Josephson vortex is of a large size along the ab
plane and squeezed in the c direction. The inter-vortex
repulsion in this geometry is highly anisotropic, and
meanwhile vortex lines feel strong layer pinning for mo-
tions along the c axis. In spite of much effort, which
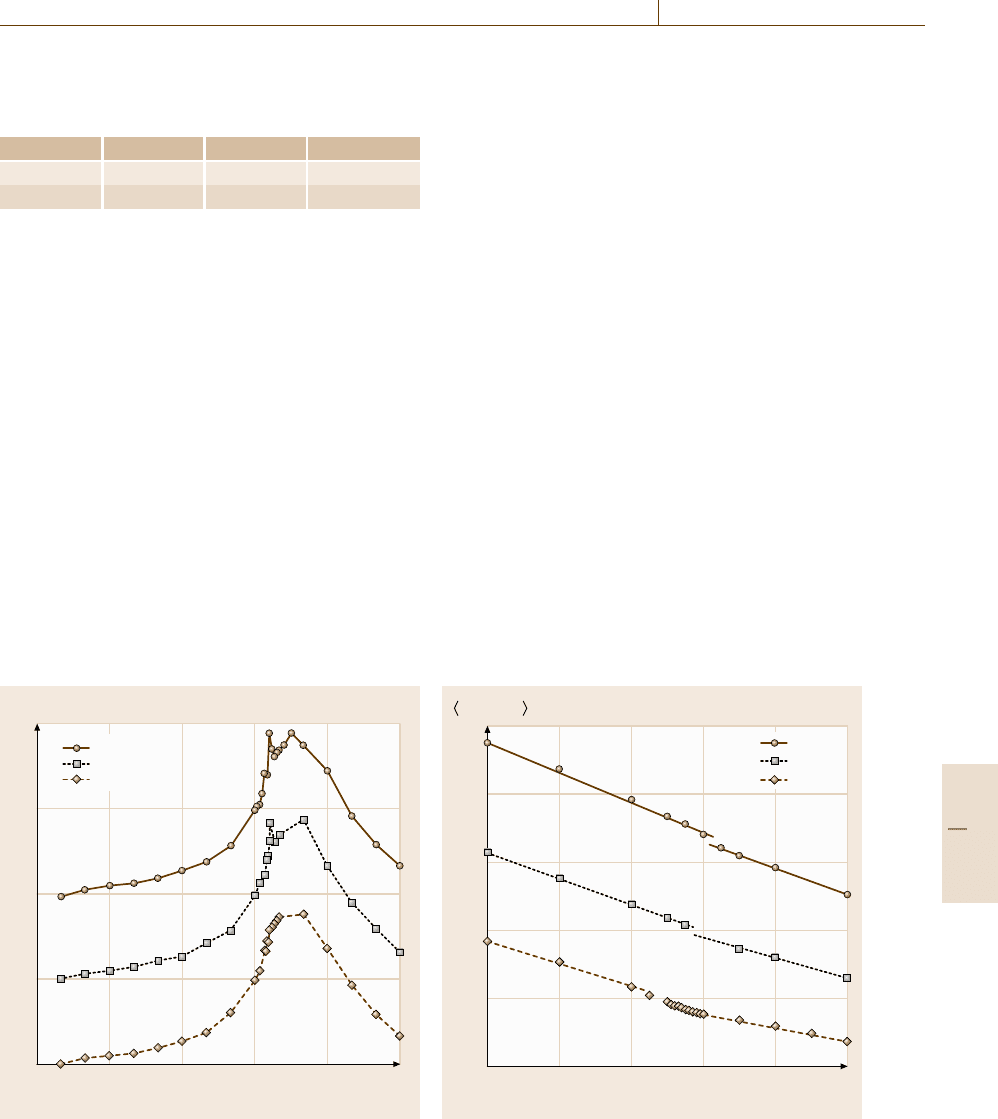
C (k
B
)
T (J/k
B
)
0 0.3 0.6 1.20.9 1.5
2.5
2
1.5
1
0.5
γ = 8
γ = 9
γ = 10
Fig. 22.22 Temperature dependence of the specific heat for
several anisotropy parameters (after [22.147]). Data for
γ = 8 and 9 are shifted by constants
certainly makes the vortex physics very rich [22.148–
158], a unified picture for possible phases, phase tran-
sitions and phase diagrams is still not yet available.
We have performed extensive Monte Carlo simulations
of the frustrated XY model (22.82). The main pre-
diction from computer simulation [22.147, 159](see
also [22.160, 161]) is that there is a multicritical point
in the B-T phase. For magnetic fields above the criti-
cal value, there is an intermediate phase characterized
by intraplane (2-D) quasi-long-range crystalline order
of vortex lines in between the liquid and the 3-D lattice.
The model Hamiltonian is given in (22.82) with
a gauge A
xy
= 0. We take Γ as the anisotropy constant
γ = 8 of the material YBa
2
Cu
3
O
7−δ
. The unit length of
our grid is then d for all the three directions. For the con-
venience of simulation, we choose f =1/32 and put the
system size as L
x
= 384, L
y
=200 and L
z
=20 with
N
v
=240 flux lines in the system.
The Specific Heat
The specific heat is displayed in Fig. 22.22. There are
sharp spikes in the specific heat for γ =8and9atT
m
0.96J/k
B
, which indicates a first-order melting. As the
total latent heats are very small, we plot in Fig. 22.23 the
expectation values for the cosine function of the gauge
invariant phase difference between neighboring layers,
which is proportional to the Josephson energy. There
T (J/k
B
)
0.9 0.92 0.94 0.980.96 1
0.18
0.16
0.14
0.12
0.1
0.08
γ = 8
γ = 9
γ = 10
cos φ
n,n+1
Fig. 22.23 Temperature dependence of the Josephson en-
ergy for several anisotropy parameters (after [22.147]).
Data for γ = 8and9areshiftedbyconstants
Part E 22.5
1142 Part E Modeling and Simulation Methods
a) b)
Fig. 22.24a,b Structure factors for Josephson vortices
S(k
x
, k
c
, y = 0) at T = 0.65J/k
B
(a) and T =0.70J/k
B
(b).Thepanels are for wave numbers within k
x
∈
[−25π/192d, 25π/192d] (horizontal)andk
c
∈[−2π/d,
2π/d] (vertical) (after [22.159])
are discontinuous jumps in this quantity for γ = 8and
9, corresponding to the spikes in the specific heat.
However, the first-order melting transition is sup-
pressed when the anisotropy parameter is increased to
γ = 10, for which the spike in the specific heat and the
discontinuous jump in the Josephson energy disappear
as in Figs. 22.22 and 22.23. It is discussed in [22.147]
that there is a critical value of f γ above which the in-
tralayer repulsion force becomes significantly stronger
than the interlayer one, such that the intralayer order
establishes first upon cooling. For a more careful discus-
sion please refer to our original paper [22.159]. It is easy
to see that this critical magnetic field should be above
S (k
x
, k
c
= π/d)/N
v
k
x
(π/192d)
0 5 10 15
γ=20
20
0.012
0.009
0.006
0.003
0
T = 0.96 J/k
B
T = 0.95 J/k
B
T = 0.92 J/k
B
T = 0.80 J/k
B
Fig. 22.25 k
x
profiles for the Bragg spots (after [22.159])
the following value when the anisotropy parameter γ is
given [22.153]
B =
1
2
√
3γ d
2
. (22.90)
To determine the value of the critical magnetic field de-
mands a lot of simulation time, and has actually not yet
been done. Nevertheless, the above relation seems to
give a reasonable estimate for moderately anisotropic
superconductors such as YBa
2
Cu
3
O
7−δ
.
Structure Factor
The above scenario has been verified by checking the
vortex correlation function. In Fig. 22.24, we present
the structure factors for f = 1/32 and γ = 20. For
T = 0.65J/k
B
there is a 3-D long-range crystalline or-
der characterized by the δ-function Bragg peaks; for
T = 0.7J/k
B
the Bragg spots smear out significantly in
the k
c
direction, corresponding to short-range correla-
tioninthec direction.
The k
x
profile for the Bragg spot at (k
x
, k
c
) =
(±2 f π/d, ±π/d) is plotted in Fig. 22.25 for several
temperatures, from which we found that the real-space
correlation functions show power-law decay with ex-
ponents 1 ≤ η ≤ 2. The cusp singularity in the k
x
profiles is suppressed at T 0.96J/k
B
where η 1.97.
The suppression of the quasi long-range order upon
S (k
x
= π/d, k
c
= π/d)/N
v
T (J/k
B
)
0 0.6 0.80.40.2 1
γ=8
γ=20
1.2
1
0.8
0.6
0.4
0.2
0
Fig. 22.26 Temperature dependence of intensity of Bragg
peaks (after [22.159])
Part E 22.5

Monte Carlo Simulation 22.6 Effects of Randomness in Vortex States 1143
heating should be a Kosterlitz–Thouless (KT) transi-
tion [22.159].
The temperature dependence of the intensity of
Bragg peaks is displayed in Fig. 22.26 is such a fash-
ion that for quasi long-range orders the intensity should
be zero at the thermodynamics limit. As our system is
finite, small values of normalized intensity can be seen
for γ = 20 which increases very slowly with decreas-
ing temperature in the region 0.7J/k
B
≤ T ≤0.95J/k
B
.
Across T
×
0.65J/k
B
where the Bragg spots become
δ-function like, the intensity increases noticeably. The
onset of 3-D long-range order is revealed as a second-
order phase transition in the 3-D XY universality class.
In a sharp contrast, the intensity of Bragg peaks for
γ = 8 increases very sharply with decreasing tempera-
ture as soon as they become observable at the melting
point T
m
0.96J/k
B
asshowninFig.22.26.
Right now experimental verifications of the multi-
critical point and the KT phase are carried on by
several groups. For an estimate, we foresee the critical
field at H ≈ 50 Tesla for YBa
2
Cu
3
O
7−δ
of γ = 8and
H ≈2 Tesla for Bi
2
Sr
2
CaCu
2
O
8+y
of γ = 150.
Since it is still not easy to simulate the vortex
states of low vortex density, namely small magnetic
field, the total phase diagram is not available merely
by the computer simulation. Recently, using the density
functional theory, we [22.162] find in certain magnetic
field regimes below that given by (22.90) a smectic
phase [22.154, 155], characterized by long-range cor-
relation along the c axis and short-range correlations in
the ab plane, that may exist in between the lattice and
liquid phases. The melting is then two-step: first-order
lattice-smectic and second-order smectic-liquid transi-
tions.
22.6 Effects of Randomness in Vortex States
It is highly nontrivial whether the vortex lattice can sur-
vive when defects are introduced into the system. The
answer depends on the dimensions of the space and the
type of defects. In the elastic theory, the Hamiltonian of
vortex states including point-like randomness is given
by
H =
c
2
[∇u(x)]
2
d
d
x −
V(x)ρ(x)d
d
x , (22.91)
where the first term stands for the simplified elastic
energy associated with deviations of flux lines u(x)
from their equilibrium positions, and V(x)andρ(x)de-
note the random potential and the density of flux lines,
respectively. Larkin [22.163,164] proposed an approxi-
mation to replace the second term by
V(x)ρ(x)d
d
x ≈
f (x)u(x)d
d
x , (22.92)
where f (x) is the Gaussian random force.
Then, the situation becomes similar to Imry–Ma’s
argument [22.165] for the random-field model. Let us
compare the energy between a polycrystal containing
domains of the linear size ∼ L with the perfect vortex
lattice. The elastic energy loss and the pinning energy
gain are proportional to L
d−2
and L
d/2
, respectively.
Since the second term is larger than the first one for
large enough L in d < 4, the vortex lattice is unstable
for infinitesimal randomness in d < 4. This simple con-
sideration turns out to be insufficient and the picture
of a Bragg glass is now established where the vortex
correlations become quasi long ranged [22.166–170].
22.6.1 Point-Like Defects
Here our Monte Carlo simulations based on the frus-
trated XY model are reviewed. Modeling of point-like
randomness is not unique in the frustrated XY model.
One possible way is to introduce a Gaussian random
variable ε
ij
with ε
ij
=0andε
2
ij
=1asJ
ij
= J +
pε
ij
[22.171]. In this definition, randomness is included
in every bond, and the strength of randomness p can
be treated as a continuous thermodynamic variable like
temperature. On the other hand, the pinning force of
these randomly-modulated interactions to vortices may
be very weak.
We introduced [22.172] point defects as the pla-
quettes which consist of four weaker couplings and are
randomly distributed in the xy plane with probability p.
Couplings are given by J
ij
=(1−ε)J (0 <ε<1) on the
point defects, and J
ij
= J elsewhere. This formulation
of point defects is schematically drawn in Fig. 22.27.As
will be seen later, most phases observed experimentally
in vortex states are reproduced by this modeling.
Bragg Glass
Monte Carlo simulations are performed for f = 1/25,
Γ = 20, p = 0.003, and various pinning strengths ε
with the system size L
x
= L
y
= 50 and L
c
= 40. The
same algorithm for the clean system discussed previ-
Part E 22.6

1144 Part E Modeling and Simulation Methods
J
(J–ε)J
Fig. 22.27 Modeling for point-like defects (after [22.172])
ε
T (J/k
B
)
0.06 0.07 0.08 0.09
Vortex
glass
Vortex
slush
Vortex
liquid
Bragg glass
Critical point
0.1
0.16
0.12
0.08
0.04
0
Fig. 22.28 -T phase diagram of vortex states with the
point defects (after [22.172,173])
ously is adopted. The ε-T phase diagram is displayed in
Fig. 22.28.
The first-order melting transition between the Bragg
glass (BrG) and vortex liquid (VL) phases is similar to
Fig. 22.29 Modeling for columnar defects (after [22.174])
that of the vortex lattice and VL phases in pure systems
as shown previously. As the strength of point-like de-
fects ε increases, the melting temperature T
m
decreases,
which shows a sharp contrast to the case with columnar
defects as will be discussed later.
The Bragg glass is destroyed when the pinning force
becomes large enough even though temperature is low,
and thus thermal fluctuations are not significant. This
randomness-induced melting was first observed numer-
ically in the random-field XY model [22.175]andthe
Lawrence–Doniach model [22.176]. The first-order na-
ture of this phase transition is clarified in more detail
by precise numerical studies on the phase boundary. We
showed [22.172] that the latent heat on the boundary
is one order smaller than that on the thermal melt-
ing line. It was also reported [22.171] that the latent
heat is vanishing within error bars while discontinuity
in other physical quantities remains observable on the
phase boundary.
Possible Vortex Glass
As a possible thermodynamic phase above the BrG, the
vortex glass (VG) phase [22.177, 178], where flux lines
are tightly pinned by point-like defects, has been con-
sidered. In the early stage of numerical simulations,
the VG-VL boundary was detected by the jump of
the correlation time [22.179] or the deviation of flux
lines [22.180]. In the frustrated XY model, the VG
phase is characterized by finite helicity modulus along
the c axis and vanishing Bragg peak [22.172]. Although
the absence of the VG was once argued [22.171], sta-
bility of the VG phase without the screening has now
been established [22.181–183]. It is noticed that the
stability of VG phase including the screening is still
unsettled [22.184,185].
Vortex Slush
There is a vortex slush phase [22.186–188] in the phase
diagram (Fig. 22.28). The vortex slush shares the same
symmetry of the liquid. The two phases are separated by
a first-order transition line characterized by the jump of
the density of dislocations in the xy plane [22.189,190].
As in the gas–liquid case, this transition line is ter-
minated by a critical point as shown in Fig. 22.28.
It is interesting to notice that even above the critical
point, a step-like anomaly of the specific heat was re-
ported [22.173,191].
22.6.2 Columnar Defects
Columnar defects created by heavy-ion irradiation
along the c axis work as strong correlated pinning
Part E 22.6

Monte Carlo Simulation 22.6 Effects of Randomness in Vortex States 1145
Melting line
p
T (J/k
B
)
0.3 0.35 0.4
Vortex
liquid
Interstitial
liquid
Bose glass
Bragg–Bose glass
or
polycrystal
Vanishing
point of
Jump
of c
44
Matching field
0.45
0.04
0.3
0.02
0.01
0
c
Fig. 22.30 p-T phase diagram for vortex states with the
columnar defects (after [22.174])
centers to the vortex lines and produce new vortex
states such as the Bose glass (BG) [22.192–194]. We
introduced [22.174] columnar defects as the corre-
lated plaquettes surrounded by four weak couplings
J
ij
=(1 −ε)J with probability p in the xy plane and
J
ij
= J elsewhere, as shown in Fig. 22.29. Since the
density of defects p plays an essential role in vortex
states with columnar defects, we tune the parameter p
while fixing ε. Parameters for simulation are Γ =5,
f =1/25, ε =0.1, and L
x
= L
y
=50 and L
c
=80.
Bose Glass
The p-T phase diagram obtained by Monte Carlo simu-
lations is displayed in Fig. 22.30. When the number
of columnar defects exceeds that of flux lines, the
BG is stable at low temperatures. Here, we concen-
trate on small densities of columnar defects, ranging
from the pure system with p = 0 to the matching case
p = f =1/25.
In order to evaluate the BG phase boundary, the
tilt modulus c
44
is evaluated. The Hamiltonian un-
der the transverse field H
⊥
is given by H
= H −
H
⊥
m
⊥
with the transverse magnetization m
⊥
,andc
44
is given [22.195]by
c
44
∼
∂m
⊥
/∂H
⊥
#
#
#
H
⊥
=0
−1
∼ N
flux
k
B
T/
$
m
⊥
2
%
#
#
#
#
H
⊥
=0
, (22.93)
aside from a coefficient. The BG phase boundary is sig-
naled by a large jump of c
44
, which is expected to be
infinite in the thermodynamic limit.
Interstitial Liquid
When the number of columnar defects is smaller than
that of flux lines and the temperature is slightly higher
than the BG transition temperature, columnar defects
still trap some flux lines, while other interstitial flux
lines can move around. This state is known as the inter-
stitial liquid (IL) [22.196]. The helicity modulus along
the c axis Υ
c
takes a finite value as long as some of the
flux lines are trapped by columnar defects. Therefore,
the vanishing of the helicity modulus Υ
c
corresponds to
the boundary of the IL region.
Possibility of Bragg–Bose Glass
Similar to the BrG phase of vortex state with point-
like defects, a Bragg–Bose glass (BBG) was proposed
in the presence of columnar defects [22.197], which
is characterized by quasi-long-range crystalline order
and diverging tilt modulus. However, stability of this
phase is not so trivial. At the ground state, flux lines
are perfectly parallel to the magnetic field and the
columnar defects. The system is then equivalent to the
two-dimensional vortex states with point defects, where
the absence of the BrG phase at T = 0 was shown nu-
merically [22.198]. Therefore, the BBG (if exists) may
be a kind of order caused by thermal fluctuations.
For small enough p and low enough temperatures,
the structure factor shows sharp Bragg peaks, which is
consistent with the BBG. As the temperature increases,
the maximum value of the structure factor S
max
q
drops
just on the BG boundary with a narrow coexistence
region, and the δ-function peak of the specific heat is
observed. These facts indicate that the first-order melt-
ing transition of the BBG phase occurs just on the BG
a) b)
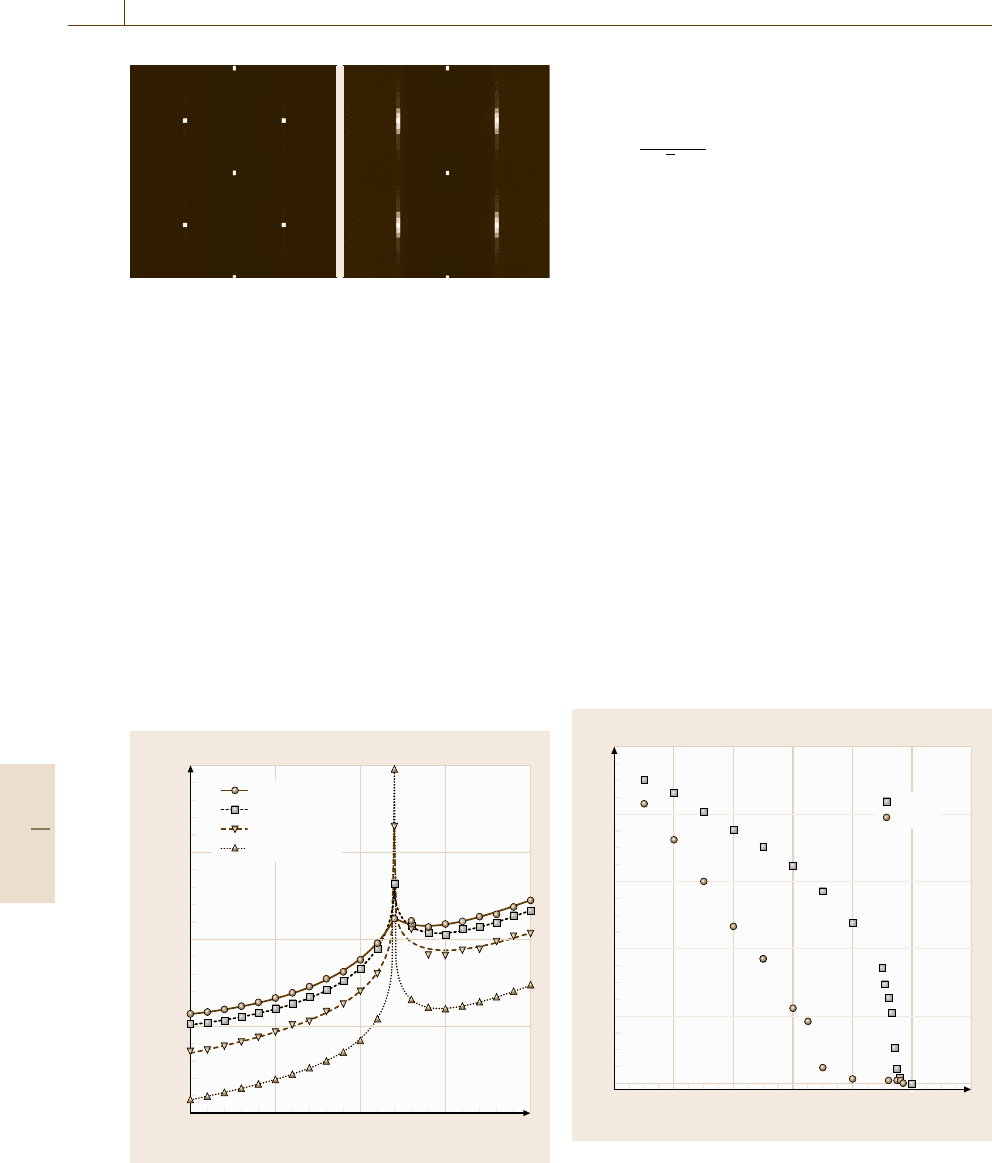
Fig. 22.31a,b Density of vortices in the xy plane averaged
along the c axis in the (a) BBG and (b) IL phases with the
same configuration of columnar defects (after [22.174]).
The defects are painted in yellow (no flux lines)tored
(filled with flux lines), and other regions are painted in vi-
olet (no flux lines)tolight blue (largest probability of flux
lines)
Part E 22.6

1146 Part E Modeling and Simulation Methods
boundary at low density of columnar defects. The BBG
at low temperature can be destroyed by introducing
more columnar defects, indicated by a sharp change
of S
max
q
. It is found that the BBG-BG phase bound-
ary is almost independent of temperature, as shown
in Fig. 22.30.
As can be seen in Fig. 22.31aforBBG phase, all
flux lines are localized and form a triangular lattice.
There exist some unoccupied columnar defects (yellow
dots). The defects far from stable positions of vortex lat-
tice remain unoccupied in the BBG phase. On the other
hand, in Fig. 22.31bfortheIL phase, most defects are
occupied unless other occupied ones are very close by
chance. Owing to such selected pinning of flux lines in
the BBG, introduction of more columnar defects to cer-
tain density enhances energy gain by trapping more flux
lines using defects close to stable positions of vortex
lattice, without destroying the lattice structure. This re-
sults in increase of the melting temperature. When p
becomes large enough, the vortex lattice will be de-
stroyed by the overwhelming pinning energy and the
BG phase becomes stable.
The above description is consistent with the simu-
lations based on the boson model [22.199], while the
simulations based on the density-functional theory re-
sults in a different picture characterized by the two-step
melting transition with the “BrG phase” surrounded by
the BG phase [22.200,201].
22.7 Quantum Critical Phenomena
Here we show several examples investigated by quan-
tum Monte Carlo simulations, which is helpful for
understanding the methodology.
22.7.1 Quantum Spin Chain
It was naively expected that low-energy excitations
of spin systems are described by spin waves. In the
spin-wave approximation, low-energy excitations are
always gapless, regardless of the length of spins.
However, Haldane predicted that in one dimension
0.005
0.004
0.003
0.002
0.001
0
Experiment
Monte Carlo
v = 2.46 (T=0)
v = 2.39 (T=0)
0.0024
0.0022
0.0020
0.0018
0.0016
0.0014
0.0012
0
0 50 100 150 200 250 300
Temperature (K)
χ (q=0;T ) (emu/mol)
51015
Fig. 22.32 Uniform susceptibility χ(q =0;T) obtained by
the quantum Monte Carlo simulation and experiments
(after [22.202])
low-energy excitations have a finite gap for integer
spin systems [22.203, 204]. This prediction was later
confirmed by numerical simulations [22.205–207]and
experiments [22.208–211]. Further, Affleck extended
Haldane’s argument to bond-alternating systems and
predicted that integer spin chains can have a gap-
less excitation with special values of the alternating
strength [22.212–214].
Some compounds that can be regarded as spin
S = 1 bond-alternating Heisenberg chains have been
found experimentally [22.215–219]. Among them,
the susceptibility of [Ni(333-tet)(μ-N
3
)](ClO
4
)
n
(333-
tet denotes tetraamine N,N
-bis(3-aminopropyl)-1,3-
propanediamine) shows a gapless behavior [22.220].
In order to confirm whether this compound can really
be described by an S = 1 bond-alternating Heisen-
berg chain, numerical simulations have been per-
formed [22.202]. Since the model is a nonfrustrated
Heisenberg model, quantum Monte Carlo simulations
can be performed without negative-sign problems as
explained in Sect. 22.3.8. Hence, the loop algorithm
(Sect. 22.3.3) is applied to this system. The comparison
between the result of the quantum Monte Carlo simula-
tion and the experimental result is shown in Fig. 22.32.
In the wide temperature range, numerical and experi-
mental data agree well. This indicates that the magnetic
properties of this compound are well described by the
S =1 bond-alternating Heisenberg chain at the gapless
point. Only in the very low temperature regime, data
show a little difference which may be due to single-ion
anisotropy of this compound.
It was also predicted that at the gapless point low-
energy properties are described by the level k = 1
Part E 22.7
Monte Carlo Simulation 22.7 Quantum Critical Phenomena 1147
14
13
12
11
10
9
8
7
0.55
0.5
0.45
0.4
0.35
0.02
S1/2AH
0.04 0.06 0.08 0.1 T
[χ (q=π;T ) T]
2
0.1 0.2
L =32
L =64
L =96
L =192
L =400
fit
S1BA
L =32
L =64
L =96
L =192
L =320
fit
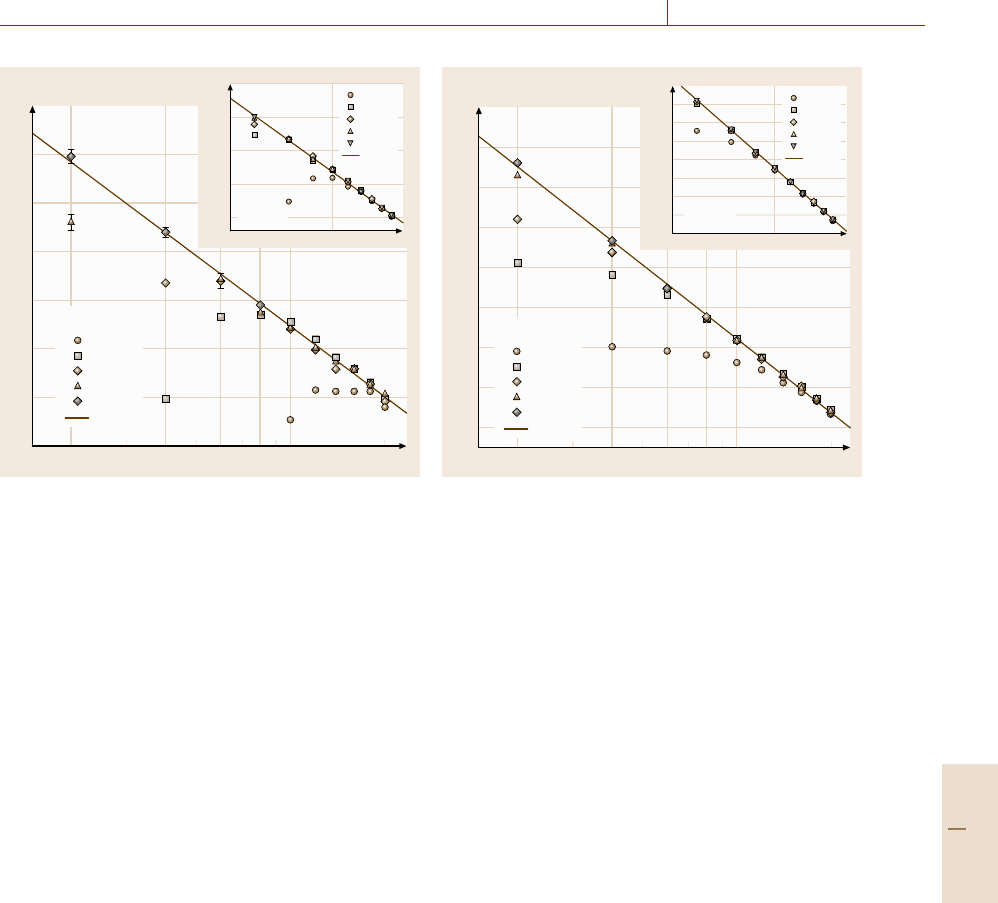
Fig. 22.33 Staggered susceptibility χ(q = π;T) obtained
by the quantum Monte Carlo simulation (after [22.202]).
S1BA and S1/2AH denote the S = 1 bond-alternating
Heisenberg chain at the gapless point and the S = 1/2
Heisenberg chain, respectively
SU(2) Wess–Zumino–Witten (WZW) model [22.212–
214], which is the same universality class as the S =1/2
Heisenberg chain. The critical properties at the gapless
point are also investigated by the quantum Monte Carlo
simulation [22.202]. It is known that in the WZW uni-
versality class staggered susceptibility χ(q =π;T )and
staggered structure factor S(q = π;T) diverge toward
the critical point [22.221,222]as
χ(q = π;T) ∝ T
−1
[ln(T
χ
/T)]
1/2
, (22.94)
S(q = π;T) ∝[ln(T
S
/T)]
3/2
. (22.95)
Figures 22.33 and 22.34 show the numerical results for
χ(q =π;T )andS(q =π;T ). The scaling properties of
(22.94)and(22.95) are clearly observed.
In this way, quantum Monte Carlo simulations
are powerful to investigate properties of spin systems.
There are many other examples to show the power of
quantum Monte Carlo simulations [22.66].
22.7.2 Mott Transition
It is widely believed that for the high-T
c
supercon-
ductivity strong correlations near the Mott transition
play an important role. In the insulating phase, there is
a magnetic order and the spin and charge excitations are
4
3.8
3.6
3.4
3.2
3
2.8
2.6
2.4
1.3
1.25
1.15
1.1
1.05
1
0.95
0.9
0.02
L =32
L =64
L =96
L =192
L =400
fit
S1BA
S1/2AH
0.04 0.06 0.08 0.1 T
[S (q=π;T ) T]
2/3
0.1 0.2
L=32
L=64
L=96
L=192
L=320
fit
Fig. 22.34 Staggered structure factor S(q =π;T) obtained
by the quantum Monte Carlo simulation (after [22.202])
separated. On the other hand, in the metallic phase, it
is expected that spin and charge degrees of freedom are
strongly coupled, and the excitations may be described
by fermionic quasi particles at least in the low electron-
density regime. The difficulty of approaching the Mott
transition comes from the complexity of the transit of
these two-types of states. Since the Hubbard and t-J
models are known to be insulators at half filling and be-
come metallic by doping, characteristic features of Mott
transitions would be described by these models.
Properties near the metal-insulator transition have
been numerically investigated by quantum Monte Carlo
simulations. For the two-dimensional Hubbard model,
Furukawa and Imada applied the auxiliary-field quan-
tum Monte Carlo method (Sect. 22.3.6) and found
nontrivial power-law behaviors toward the Mott transi-
tion point [22.223]: The compressibility κ and the spin
structure factor S(Q) diverge as
κ ∝δ
−1
, (22.96)
S(Q) ∝δ
−1
, (22.97)
where δ denotes the doping concentration. Equation
(22.97) suggests that the antiferromagnetic correlation
length ξ
m
diverges as
ξ
m
∝δ
−1/2
, (22.98)
assuming that the spin–spin correlations behave as
S
0
S
r
∝e
iQr
· e
−r/ξ
m
. These features are observed by
Part E 22.7
