Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing

Подождите немного. Документ загружается.

1118 Part E Modeling and Simulation Methods

and magnetic polarization of a magnet, upon various

external conditions such as temperature, pressure and

magnetic ﬁeld, instead of the detailed trajectories of

individual particles. The statistical mechanics is such

a disciplinary, which reveals simple rules governing

systems of huge numbers of components. In many inter-

esting cases, unfortunately, statistical mechanics cannot

provide a ﬁnal compact expression for the desired phys-

ical quantities because of the many-body effect of the

interactions among components, although the bare in-

teraction is two-body. Many approximate theories have

been developed which make the ﬁeld called condensed

matter physics very rich. With the huge leaping of

power of computers, the Monte Carlo approach based

on the principle of statistical mechanics has been de-

veloped in the recent decades. This chapter is devoted

to introducing the basic notions for the Monte Carlo

method [22.1], with several examples of application.

22.1.1 Boltzmann Weight

According to the principle of statistical mechanics, the

probability for a particular microscopic state appearing

in an equilibrium system attached to a heat reservoir

with temperature T is given by the Boltzmann weight

= e

−βE



−βE

≡ e

−βE

/Z , (22.1)

where β =1/k

T, E

the energy of the system at the

particular state, and Z the partition function. The ex-

pectation value of any physical quantity, such as the

magnetic polarization of a magnet, can be evaluated by

O=



−βE

. (22.2)

The difﬁculty one meets in applications is: there are too

many possible states such that it is practically unable

to compute the partition function and the expectation

values for desired physical quantities.

22.1.2 Monte Carlo Technique

The Monte Carlo techniques overcome this difﬁculty by

choosing a subset of possible states, and approximate

the expectation value of a physical quantity by the av-

erage within the subset of states of limited number. The

way for picking up the subset of states can be speci-

ﬁed by ourselves, and is very crucial to the accuracy

of the estimation thus made. A successful Monte Carlo

simulation thus relies heavily on the way of sampling.

Importance Sampling

One can regard the statistical expectation value as a time

average over the states a system passes through the

course of a measurement. This suggests that we can

take a sample of the states of the system such that

the possibility of any particular state being chosen is

proportional to its Boltzmann weight. This importance

sampling method is the simplest and most widely-used

in Monte Carlo approaches. It is easy to see that the esti-

mation for the desired expectation value is given simply

O



i=1

/M , (22.3)

since the Boltzmann weight has been already involved

into the process of sampling. This estimation is much

more accurate than a simple sampling process, espe-

cially at low temperatures where the system spends the

large portion of time in several states with low energies.

The implementation of the above importance sam-

pling is achieved by Markov processes. A Markov

process for Monte Carlo simulation generates a Markov

chain of states: starting from the state a, it indicates

a new one b, and upon inputting b it points the third one

c, and so on. A certain number of the states at the head

of these Markov chains are dropped, since they depend

on initial state a. However, after running a sufﬁciently

long time, the picked states should obey the Boltzmann

distribution. This goal is guaranteed by the ergodicity

property and the condition of detailed balance.

Ergodicity

This property requires that any state of the system can

be reached via the Markov process from any other state

supposing we run it sufﬁciently long. The importance

of this condition is very clear since otherwise the miss-

ing states will have zero weight in our simulation which

is not the case in reality. It is noticed that one still has

room to set the direct transition probability from one

state to many others to zero, as usually done in many

algorithms.

Detailed Balance

This condition is slightly subtle and requires some con-

sideration. For the desired distribution vector p, with the

components of the vector being the Boltzmann weight

for each state, suppose we ﬁnd an appropriate Markov

process characterized by a set of transition probabilities

among possible states such that



P(i → j) =



P( j →i) , (22.4)

Part E 22.1

Monte Carlo Simulation 22.1 Fundamentals of the Monte Carlo Method 1119

where p

is the probability of the state i and P(i → j)

the transition probability from i-state to j-state. The

above condition is necessary since the desired distribu-

tion, namely the Boltzmann distribution, is the one for

equilibrium state. However, the Markov process satis-

fying the above condition does not necessarily generate

the desired distribution, even when the Markov chain is

run long enough. Actually, it is possible that a dynamic

limit cycle is realized as



(t +n) = P



(t) (22.5)

with n > 1, so that the desired distribution p can never

be reached. In order to avoid this situation, we set the

detailed balance condition

P(i → j) = p

P( j →i) . (22.6)

It is easy to see that this condition eliminates the possi-

bility of limit cycles. Then from the Perron–Frobenuius

theorem, it can be shown that the desired distribution p

is the only one that can be generated by the transition

matrix P.

To be short, a Markov process satisfying the condi-

tions (i) the ergodicity condition, (ii)



P(i → j) =1,

and (iii)

P(i → j)/P( j → i) = p

= e

−β(E

−E

)

(22.7)

will generate the Boltzmann distribution at equilibrium.

Acceptance Ratio

There is still freedom when composing the transition

probabilities. One can take a selection probability g and

the acceptance ratio A such that

P(i → j) = g(i → j)A(i → j) . (22.8)

For simplicity, one usually takes the constant selection

probability for all possible states during the one-step

transition. As for the acceptance ratio, we can take them

as large as possible provided they satisfy the condition

(22.7), which makes the Markov chain move more efﬁ-

ciently around the sampling space. It is easy to see that

the acceptance ratio is given by

A(i → j) =



−β(E

−E

)

, for E

−E

> 0 ;

1, otherwise .

(22.9)

This is the Metropolis algorithm [22.2].

With the selection probability and the acceptance

ratio determined, a Monte Carlo simulation goes like

the following: from a given initial state we pick up

a candidate for the next state out of the possible ones

according to the selection probability; then we check

if the candidate state is to be accepted according to

the probability speciﬁed by the acceptance ratio. This

routine is repeated for sufﬁciently long time before we

insert a measurement step where we calculate physical

quantities for the realized state.

It is then clear that the Markov chain of states thus

generated is stochastic, which is the most important

feature of the Monte Carlo techniques in comparison

with other deterministic methods such as molecular dy-

namics. The rules which specify a particular simulation

algorithm govern the distribution of the realized states

when a large number of states are piled up.

22.1.3 Random Numbers

The stochastic property of Monte Carlo simulations

comes in because one chooses a new state from the old

one in a random fashion. This process is realized by ran-

dom numbers. Therefore, generation of a sequence of

random numbers is of crucial importance for accurate

Monte Carlo simulations. Of course, as long as such

a sequence is generated by a deterministic procedure

written in a computer code, it cannot be really random.

It is usually called quasi random provided it satisﬁes the

following two conditions characteristic to true random

numbers.

Condition I: The period of the quasi random numbers

should be longer than the total length of simulations.

Condition II: The quasi random numbers should be

k-dimensional equidistributed with large enough k.In

other words, all possible sets consisting of k sequential

numbers appear with the same frequency in a period,

except the one of k zeros.

Classical Random Number Generators

The linear congruential sequence is given by

i+1

=ax

+b mod 2

, i =0, 1,... , (22.10)

where w stands for the number of bits of random num-

bers x

,anda and b are suitable sets of numbers which

maximizes the period of the quasi random numbers to

. The merit of this sequence is its simplicity. How-

ever, it has several shortcomings. First, the period is not

sufﬁciently long even with w =31. Second, a random

number is determined only by the previous one, and

there exists strong correlation among sequential num-

bers. Third, the multiple operation is time consuming.

Part E 22.1

1120 Part E Modeling and Simulation Methods

These shortcomings are overcome by the general-

ized feedback shift register (GFSR)

i+n

i+m

⊕x

, i = 0, 1,... , (22.11)

where ⊕ denotes the exclusive- or logical operation.

The two integers n and m are chosen so that t

is an nth order primitive polynomial of t. When the ini-

tial seeds x

, x

,...,x

n−1

are prepared appropriately,

the period of this sequence is 2

−1. This period is

due to the independence of each bit. Since each step

only includes one logical operation, this algorithm is

very fast. However, statistical properties of this fam-

ily of random numbers is still not very satisfactory, as

shown by large-scale Monte Carlo simulations of the

two-dimensional Ising model [22.3] for which an exact

solution is available.

Advanced Generators

In order to increase the period of the sequence of quasi

random numbers, the twisted GFSR (TGFSR) has been

introduced [22.4,5]

i+n

i+m

⊕x

A, i =0, 1,... , (22.12)

where A is a w ×w sparse matrix

A =

⎛

⎜

⎝

w−1

w−2

··· a

⎞

⎟

⎠

. (22.13)

Here a

w−1

,...,a

take 1 or 0 so that ϕ

)is

primitive with ϕ

(t) the characteristic polynomial of A.

This operation mixes the information of all bits, and

the period of each bit increases up to 2

−1. In order

to accomplish the equidistribution property, tempering

operations consisting of certain bitshift and bitmask

logical operations are introduced in each step. Based

on these two operations the so-called TT800 algorithm

with w =32, n = 25 and m = 7 exhibits the period

800

−1 and 25-dimensional equidistribution.

A further improved generator known as the

Mersenne Twister is proposed [22.6]

i+n

i+m

⊕



i+1



A, i = 0, 1,... , (22.14)

where the matrix A is determined similarly to the

TGFSR. The key point is to use the incomplete array,

with



i+1



standing for the operation to combine

the upper (w −r) bits of x

and the lower r bits

of x

i+1

. This operation drops the information of the

lower r bits of x

, and consequently the period is re-

duced from 2

−1to2

−1, with p =nw −r.On

the other hand, if the period can be chosen as a prime

number, there exists an algorithm which evaluates the

characteristic polynomial ϕ

(t) with O(p

) compu-

tations. Then, the period can be extended thanks to

the r degrees of freedom. Taking w =32, n = 624,

m = 397 and r =31 results in a Mersenne prime num-

ber p =19 937, namely the MT19937 algorithm has

the period 2

19 937

−1 and 623-dimensional equidistri-

bution. Owing to such an astronomical period and good

statistical property on a rigorous mathematical basis,

this algorithm is now becoming the standard quasi

random number generator both in academic and com-

mercial uses [22.7].

22.1.4 Finite-Size Effects

In the thermodynamic limit, many physical quantities

diverge at the phase transition. Although all of them

take ﬁnite values in a ﬁnite system, diverging properties

can be evaluated from the scaling behavior of a series of

ﬁnite-size systems.

First-Order Phase Transition

In a ﬁrst-order phase transition, divergence of physi-

cal quantities at the transition temperature is δ-function

like in the thermodynamic limit. The size dependence

of the divergent quantity and the transition temperature

in ﬁnite systems should be

Q(L, T

(L)) = Q

, (22.15)

(L) =T

(∞) +C



−d

+···, (22.16)

Note that the constant term Q

is continuous from

outside the transition regime, and thus is important

physically as the divergent term.

Second-Order Phase Transition

In a second-order phase transition, physical quantities

diverge in a wide range around the critical temperature

in the thermodynamic limit as

Q(T) ∼

T −T

−ϕ

, (22.17)

where ϕ is the critical exponent of quantity Q. A typical

example is the susceptibility of a ferromagnet. Correla-

tions between order parameters develop in the following

Part E 22.1

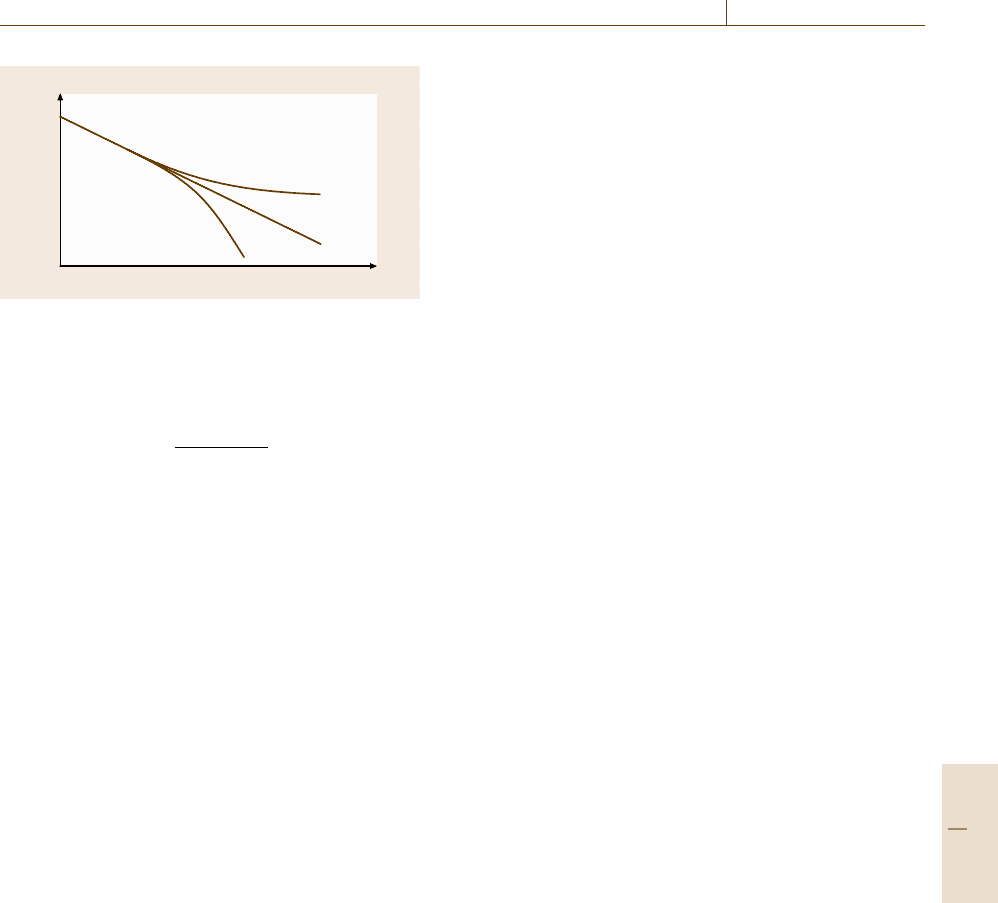
Monte Carlo Simulation 22.2 Improved Algorithms 1121

log m

log t

(a) (b)

(c)

Fig. 22.1 Schematic ﬁgure of nonequilibrium relaxation of

order parameter from a fully polarized conﬁguration for (a)

T > T

,(b) T = T

and (c) T < T

way

m

−m



∼

−|i−j|/ξ

|i − j|

d−2+η

, (22.18)

ξ ∼|T −T

−ν

, (22.19)

where m

stands for the order parameter at position i,

and ν and η are the critical exponents for the correlation

length and critical correlation function. While the criti-

cal temperature T

depends on details of systems such as

lattice structures, the critical exponents are not changed

by such details, a property known as the universality of

critical phenomena.

In a ﬁnite system, phase transition is supposed to

take place at the temperature where a correlated clus-

ter becomes as large as the system size, namely ξ ∼ L.

Finite-size scaling theory claims that physical quanti-

ties around the critical temperature can be expressed as

a function of L/ξ in the following fashion

Q(L, T ) ∼ L

ϕ/ν



1/ν

(T −T

)



, (22.20)

where f

(x) is a scaling function.

Several statements can be derived from the ﬁnite-

size scaling form (22.20): (1) At T = T

, this form

is reduced to Q(L, T

) ∼ L

ϕ/ν

, which stands for the

power-law size dependence at the critical temperature.

(2) When L

−ϕ/ν

Q(L, T) is plotted versus L

1/ν

(T −

), the curves for different L should collapse to each

other in the vicinity of T

provided T

, ν and ϕ are

known. Alternatively, one can use this so-called ﬁnite-

size scaling plot to evaluate the critical point and critical

exponents.

22.1.5 Nonequilibrium Relaxation Method

As discussed above, measurement of physical quanti-

ties should be made after equilibration of the system.

However, the relaxation process also contains valuable

information of equilibrium state, such as the transition

point and critical exponents. As an example, we con-

sider the magnetic polarization of a ferromagnet, which

presuming nonvanishing value only below the transi-

tion temperature as m(T) ∼(T

−T)

. If one starts from

a fully polarized conﬁguration, the order parameter m

decays exponentially to zero as MC update proceeds

for T > T

; it converges to a ﬁnite value for T < T

,as

showninFig.22.1. The dynamical scaling form [22.8,9]

in the thermodynamic limit is given by

m(T ;t) ∼t

−β/(zν)



1/(zν)

(T −T

)



, (22.21)

where z is the dynamical critical exponent. At T = T

(22.21) reduces to

m(T

;t) ∼t

−β/(zν)

. (22.22)

Therefore, it is possible to evaluate the critical

temperature T

and a combination of critical ex-

ponents β/(zν) [22.10–13]. Another combination of

critical exponents 1/(zν) is evaluated from the “ﬁnite-

time” scaling of (22.21). Extensions to quantum sys-

tems [22.14–16] and Kosterlitz–Thouless [22.17]and

ﬁrst-order [22.18] phase transitions are possible.

22.2 Improved Algorithms

The conventional Monte Carlo algorithm explained

above suffers from the problem of slow relaxation

in cases such as nucleation process in ﬁrst-order

phase transitions, critical slowing down in the vicinity

of second-order phase transitions, and complex free-

energy landscape of random and/or frustrated systems.

Several improved algorithms are proposed and shown

to be very efﬁcient. Readers can refer to [22.19]for

a well-written review.

22.2.1 Reweighting Algorithms

Suppose the number of states between E and E + dE

is given by D(E)dE with the density of states (DOS)

Part E 22.2

1122 Part E Modeling and Simulation Methods

D(E), the probability for the system presuming energy

E is P(E, T) ∼ D(E)e

−βE

, known as the canonical

distribution. If the canonical distribution at a tempera-

ture β

is given, that at β is obtained by the reweighting

formula [22.20]

P(E;T) =

−(β−β

P(E;T

)



−(β−β

)ε

P(ε;T

)dε

. (22.23)

Since the histogram P(E;T

) has a sharp peak around

the averaged energy of the system at T

, P(E;T) can be

evaluated from P(E;T

) with small enough statistical

errors only if T is close enough to T

. This limitation

can be overcome by taking data for several temperatures

around the target one [22.21,22].

The essential point of the histogram method is to no-

tice that the probability distribution used in simulations

can be different from that used for evaluating thermal

averages of physical quantities, namely the Boltz-

mann distribution. In the multicanonical method [22.23,

24], the simulated probability distribution is taken as

P(E;T) ≈1/E

(T), where E

(T ) stands for the range

of the energy covered in simulations at temperature T.

The reason that the multicanonical simulation works ef-

ﬁciently can be seen taking the example of a ﬁrst-order

phase transition. Since the canonical distribution has

a sharp peak around the equilibrium energy, nucleation

processes governed by the two free-energy minima with

ﬁnite separation results in slow relaxation. This difﬁ-

culty is overcome by the broad energy range covered by

the multicanonical weight.

Since the DOS D(E) is not known a priori, it should

be evaluated in preliminary runs, and the approximate

DOS D

(E;T) is utilized in simulations. The probabil-

ity distribution

(E;T) = D

−1

(E;T )D(E)/E

(T) (22.24)

does not have to be completely ﬂat, and the reweighting

formula is given by

P(E;T) =

−βE

(E;T)P

(E;T)



−βε

(ε;T )P

(ε;T)dε

. (22.25)

From a practical point of view, construction of the

ﬂat histogram (or precise estimation of the DOS)isthe

crucial point of the multicanonical method, and vari-

ous algorithms have been proposed [22.25–30] after the

original one. In all these algorithms, the DOS is eval-

uated by accumulating the entry number of a random

walk in the energy space. As the system size increases,

the deviation of the DOS grows exponentially, and the

estimation within limited preliminary runs by simple

accumulation becomes difﬁcult.

In order to overcome this difﬁculty, a new algo-

rithm [22.31, 32] was proposed based on a “biased”

random walk in the energy space

0. Set i =0, D(E) ≡1andn = 1.

1. Select a site at random and measure the initial en-

ergy E

2. Choose a Monte Carlo move to the state with en-

ergy E

by the transition probability p(E

→ E

)

=min[D(E

)/D(E

), 1].

3. Update the DOS at the energy of the chosen state as

D(E) → D(E) f

, with a modiﬁcation factor f

> 1.

4. If n < N,setn → n +1 and go to step 1.

5. If n = N,set f

→ f

i+1

(< f

), i → i +1, n = 1,

rescale the DOS andgotostep1.

6. Continue this process until f

→1.

The essential point of this algorithm is the intro-

duction of the modiﬁcation factor f

.When f

and N

aretakensothat f

is comparable to the total num-

ber of states, the deviation of the DOS is reproduced in

the early stage of the iteration. Of course, f

> 1 means

that the detailed balance condition is not satisﬁed (in

this sense this algorithm does not belong to Monte Carlo

ones), and the DOS during the iteration has a systematic

discrepancy from the equilibrium one. The true DOS is

obtained at the ﬁnal stage of the iteration, where f

eventually holds.

The reweighting algorithm discussed above has

a bonus that some physical quantities not available in

conventional Monte Carlo algorithm can be treated by

this method. For example, the energy dependence of

the free-energy landscape can be evaluated [22.33, 34],

which is suitable for the analysis of the ﬁrst-order phase

transition.

22.2.2 Cluster Algorithm and Extensions

In the vicinity of the critical temperature T

of a se-

cond-order phase transition, the correlation time τ of

a physical quantity Q deﬁned in

Q(t

)Q(t

+t)∼e

−t/τ

, (22.26)

diverges as τ ∼ (T −T

)

−zν

, where z is a dynamical

critical exponent. The critical slowing down makes

computer simulations around the critical point very time

consuming. In order to overcome this difﬁculty, the

cluster algorithm (Swendsen–Wang (SW) algorithm)

was proposed [22.35].

Part E 22.2

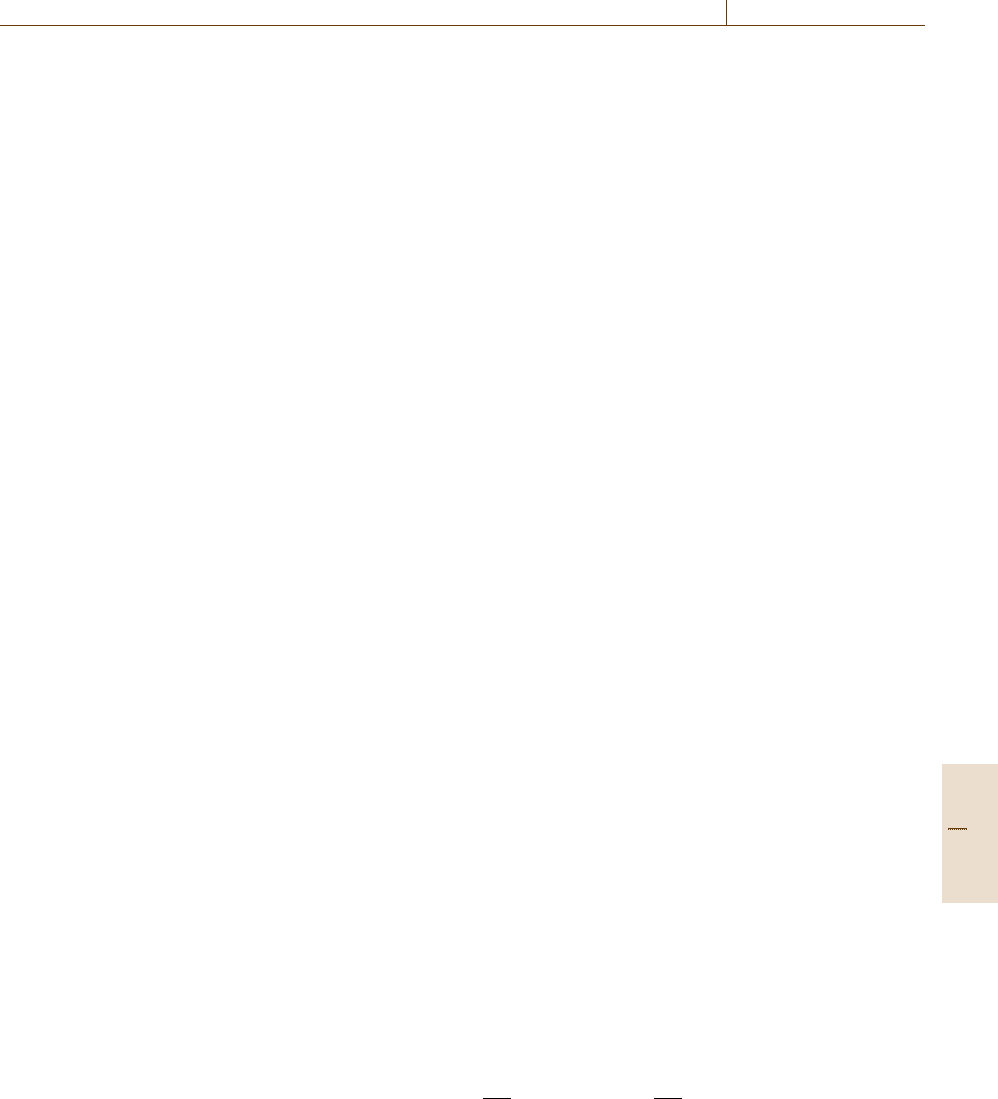
Monte Carlo Simulation 22.2 Improved Algorithms 1123

Here we explain this algorithm using the Ising

model

−βH = K



i, j

,σ

=±1 . (22.27)

First, we consider the Hamiltonian H

l,m

in which the

interaction between sites l and m are removed. Then,

we deﬁne the conditional partition functions Z

l,m

and

l,m

for σ

=+1and−1by

l,m

=Tr

−βH

l,m

, (22.28)

l,m

=Tr

−βH

l,m

,−1

. (22.29)

The partition function is expressed as

Z =Tr

−βH

= e

l,m

+ e

−K

l,m

. (22.30)

Using

l,m

=Tr

−βH

l,m

= Z

l,m

, (22.31)

we can rewrite (22.29)as

Z = e





1− e

−2K



l,m

+ e

−2K

l,m



. (22.32)

This expression can be interpreted as: “If the spins at

sites l and m are parallel, create a bond with the proba-

bility p =1− e

−2K

.” When this procedure is repeated

for all nearest-neighbor pairs of spins, each spin is as-

signed to one of the clusters. The system is now mapped

on a percolation problem with N

clusters [22.36,37]

Z =Tr p

(1 − p)

, (22.33)

where b is the number of bonds and n is the number of

interactions which do not form bonds, and the trace is

taken for all possible conﬁgurations of clusters. In each

Monte Carlo step, we assign a new Ising variable for

each cluster independently. This nonlocal update using

percolation clusters reduces signiﬁcantly the relaxation

time.

It was then proposed [22.38] that one can ﬂip a sin-

gle cluster in one step which is grown from a randomly

chosen site. This process improves the efﬁciency of the

SW cluster algorithm [22.39].

The algorithm discussed above can be applied to the

Heisenberg model [22.38]

−βH = K



ij

·S

, S

=1 , (22.34)

using an operator R(r) with respect to a randomly cho-

sen unit vector r in the spin space

R(r)S = S−2(S·r)r ,

(22.35)

and a spin cluster is formed in the procedure: “If the

spins at sites l and m satisﬁes M ≡ (S

·r)(S

·r) > 0,

create a bond with the probability p =1 − e

−2KM

.”

This rule is a natural extension of the SW algorithm in

the Ising model (22.27), and r is updated in each Monte

Carlo step. A similar extension has been made to the

six-vertex model [22.40]. Since this model is a classical

counterpart of the quantum Heisenberg model, this ex-

tension enabled the cluster-update version of quantum

Monte Carlo simulations, as will be discussed later.

Further developments of the cluster algorithm took

place in connection with percolation theories. The in-

vaded cluster algorithm [22.41,42] which automatically

tunes physical parameters to the critical point is a typ-

ical example. It turns out that a simple algorithm to

tune the probability p directly until critical percolation

is observed [22.43] works better.

Another important progress is the worm algo-

rithm [22.44], which enables accelerated dynamics as

fast as the cluster update within the local update.

Although this algorithm is based on the closed-path

conﬁgurations appearing in high-temperature expan-

sions, it shares the fundamental concept with the cluster

algorithm, namely Monte Carlo simulations in alter-

native representations of original systems. Since this

algorithm exhibits its merits more clearly in quantum

Monte Carlo simulations, it will be explained later in

this chapter.

22.2.3 Hybrid Monte Carlo Method

As far as the ergodicity and detailed balance condi-

tion are satisﬁed, any kind of update process can be

adopted in a certain Monte Carlo algorithm. Then, it

is interesting to hybridize Monte Carlo and molecular

dynamics (MD) simulations. Since MD process corre-

sponds to a forced particle move on an equal-energy

surface, it is expected to be effective in frustrated sys-

tems at low temperatures. An implementation in this

direction is formulated for the Heisenberg spin glass

model [22.45,46]

H =



ij

·S

, S

=1 , (22.36)

with the equation of motion



= S

× H

, H

∂H

∂S



. (22.37)

The MD treatment for all spins is inserted in each Monte

Carlo step for certain time intervals.

Part E 22.2

1124 Part E Modeling and Simulation Methods

22.2.4 Simulated Annealing

and Extensions

In complex free-energy landscapes of random and/or

frustrated systems as shown in Fig. 22.2, conven-

tional Monte Carlo algorithms result in trapping to

a metastable state. Applications of the multicanoni-

cal and cluster algorithms brought some progress but

the results were not so satisfactory, since for exam-

ple frustrations suppress the formation of large clusters.

One therefore needs special treatments for this class of

problems.

Fig. 22.2 Schematic ﬁgure of a complex free-energy land-

scape

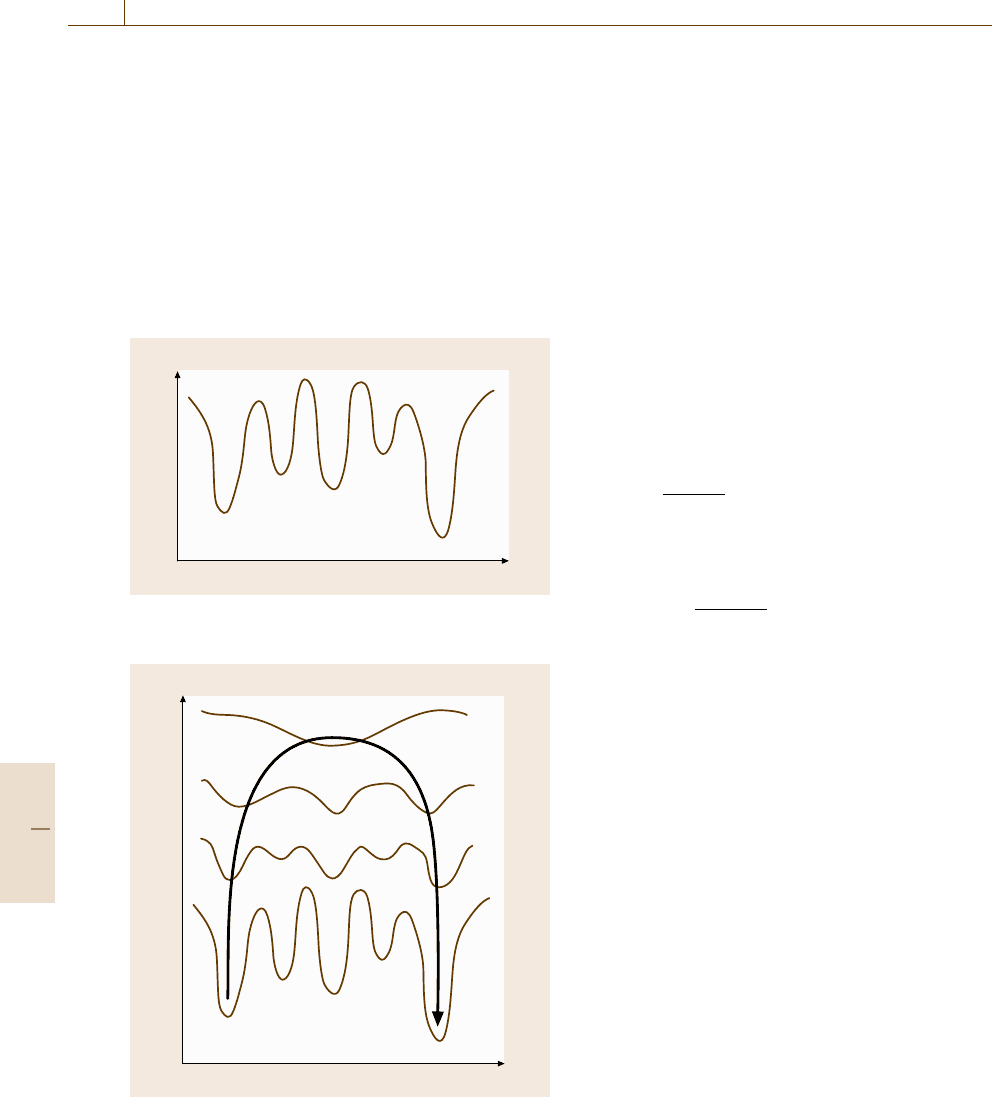
Fig. 22.3 Deep valleys of the free-energy landscape at

low temperatures (at the bottom) can be bypassed with

high-temperature conﬁgurations (upper ones correspond to

higher temperatures)

The simulated annealing [22.47] was originally pro-

posed for optimization problems, namely searching the

state which minimizes a cost function. The cost func-

tion can be taken as the energy of a physical system.

One can then introduce an auxiliary temperature,and

deﬁne a free energy at ﬁnite temperatures. The beneﬁt is

that one can then search the global energy minimum via

some passes activated naturally by ﬁnite temperatures.

The simulation is started from a high temperature, and

the system is cooled down gradually.

Simulated Tempering

In the simulated tempering [22.48, 49] the inverse tem-

perature β is treated as a dynamical variable, such that

both the cooling and heating processes are implemented

in the algorithm. The reason this algorithm works well

is explained in Fig. 22.3. The probability distribution of

the original system

P(x) =

−βH(x)

Z(β)

, Z(β) =



−βH(x)

, (22.38)

is extended to a larger parameter space of x and {β

}

(m = 1, 2,...,M)as

P(x,β

) =

−β

H(x)

Z(β

)

, (22.39)

∝exp



+log Z(β

)





=1 . (22.40)

One choice of the function g

is g

=−log Z(β

which results in

= 1/M. That is, all β

are visited

equally.

Choosing several discrete inverse temperatures can

make the simulation efﬁcient, and the optimal number

and distribution of {β

}are estimated as follows [22.49,

50]. First, the acceptance ratio of the ﬂip between dif-

ferent temperatures is given by

exp



−(β

H(x

)−β

m+1

H(x

m+1

))



≈exp



−(Δβ)

dH/ dβ



=exp



−(Δβ)

NC/β



where N and C are the number of particles and the

speciﬁc heat, respectively. In order to keep the accep-

tance ratio independent of the system size, Δβ ∼ N

−1/2

or M ∼ N

1/2

should be satisﬁed. If C diverges at the

critical temperature, one should take M ∼ N

[1+α/(dν)]/2

with the critical exponent α of C and the space dimen-

sion d.

Next, each β

is determined iteratively in prelimi-

nary runs. A new set {β



} is constructed from the old

Part E 22.2

Monte Carlo Simulation 22.2 Improved Algorithms 1125

set {β

} as



=β

, (22.41)



=β



m−1

+(β

−β

m−1

)

(m = 2,...,M) , (22.42)

c =

M −1



m=2

, (22.43)

with β

<β

< ···<β

. The acceptance ratio p

is also evaluated during preliminary runs. The above

procedure arrives at equilibrium when all values of {p

}

become equal, which is consistent with the initial choice

of g

Monte Carlo simulations are performed using the

above sets of {β

} and {g

}.Sinceg

only depends

on β

, update without changing β

is the same as

the standard one, and the weight for update of β

proportional to e

−β

H+g

. Measurements on physical

quantities are made similarly to the conventional Monte

Carlo algorithm at each β

Exchange Monte Carlo

Instead of treating one system as in the simulated

tempering, the exchange Monte Carlo method [22.50]

takes M replicated systems at β

(m = 1, 2,...,M),

and exchanges the conﬁgurations between replicas of

close temperatures. The optimal distribution of β

evaluated similarly to that in the simulated temper-

ing as given in (22.41)–(22.43). Update in a replica

is the same as the conventional one, and exchange of

replicas at β

and β

m+1

is introduced by comparison

of the weights exp



−β

H(x

) −β

m+1

H(x

m+1

)



and

exp



−β

H(x

m+1

) −β

m+1

H(x

)



. This algorithm can

be regarded as a parallelized version of the simulated

tempering, and is often called parallel tempering.

This algorithm has several advantages compared

with the simulated tempering. First, it is unnecessary to

introduce the nontrivial function g

. Since determina-

tion of g

(or equivalently Z(β

)) is complicated and

time consuming, this property simpliﬁes the coding and

accelerates simulations. Second, existence of ﬁxed sets

of β

throughout simulations is suitable for observing

the replica overlap, which is important in the study of

spin glasses. Third, this algorithm ﬁts very well with

parallel coding. Most calculations can be done inde-

pendently in each replica (i. e., in each CPU), and only

information on exchange rates and temperatures have to

be sent to other CPUs.

22.2.5 Replica Monte Carlo

The replica Monte Carlo [22.51] implemented for spin

glass models can be regarded as a mixture of the ex-

change Monte Carlo and the cluster algorithm. Consider

the Ising spin glass model

H =−



ij

β J

, (22.44)

and take M replicas. The pair Hamiltonian of two close

temperatures is deﬁned as (for simplicity, m = 1)

pair

(σ

,σ

) =−



ij



+β



(22.45)

Using a new Ising variable τ

(m)

= σ

(m)

(m+1)

,(22.45)

is written as

pair

(σ

;τ

) =−



ij



+β



(22.46)

The pair Hamiltonian is divided into clusters within

which τ

=+1 is satisﬁed. When each cluster is rep-

resented by an effective Ising variable η

(m)

with the

index a of clusters, the pair Hamiltonian is expressed





=−



a,b

a,b

, (22.47)

a,b

=(β

−β

)



i∈a, j∈b

. (22.48)

The cluster update is introduced as Monte Carlo ﬂips of

the variable η

starting from conﬁgurations with all-up

spins.

After the cluster ﬂip, original Ising variables are

changed as σ

1,2

← η

1,2

for i ∈ a, and conventional

Monte Carlo ﬂips are performed in each replica to as-

sure the ergodicity.

In the representation (22.46), the exchange Monte

Carlo corresponds to a simultaneous ﬂip of all τ

=−1

clusters. Although the present algorithm was proposed

as early as the cluster algorithm itself and much earlier

than the exchange Monte Carlo, it has not been used

so popularly to date due to complex coding and limited

applicability in comparison with the exchange Monte

Carlo. However, a recent study [22.52] showed that in

two dimensions this algorithm is much faster than the

exchange Monte Carlo.

Part E 22.2

1126 Part E Modeling and Simulation Methods

22.3 Quantum Monte Carlo Method

The quantum Monte Carlo method is a powerful method

to investigate both ﬁnite- and zero-temperature proper-

ties of quantum systems. The results are exact within

error bars. This method can be applied to large-size

systems in any dimensions. However, it has a prob-

lem when applied to the systems with large frustrations

or strong correlations. In such systems, almost half of

samples have negative weights, and Monte Carlo simu-

lations do not work well. Hence, readers had better

take care in using the quantum Monte Carlo method for

such systems. The negative-sign problem is explained

in Sect. 22.3.8.

There are several types of quantum Monte Carlo

algorithms. Depending on the model, the most suit-

able algorithm should be chosen: For spin systems

without magnetic ﬁelds, the cluster algorithm is ef-

fective (Sect. 22.3.3). Under magnetic ﬁelds, the worm

algorithm or the directed-loop algorithm is better

(Sect. 22.3.5). The continuous-time algorithm makes

simulations efﬁcient (Sect. 22.3.4). For electron sys-

tems, the auxiliary-ﬁeld algorithm is appropriate, es-

pecially for the Hubbard model (Sect. 22.3.6). To

investigate the ground-state properties, projection meth-

ods are suitable (Sect. 22.3.7).

There are other Monte Carlo methods to investigate

quantum systems. Here, we only consider the quantum

Monte Carlo algorithms by which results converge to

the exact value in principle. Hence, approximate meth-

ods like variational Monte Carlo methods or ﬁxed-node

approximations are beyond our scope.

22.3.1 Suzuki–Trotter Formalism

Quantum Monte Carlo simulations in d-dimensional

systems are generally performed through mapping to

(1)

1 (1)2 N

... 1 (1)2 N

...

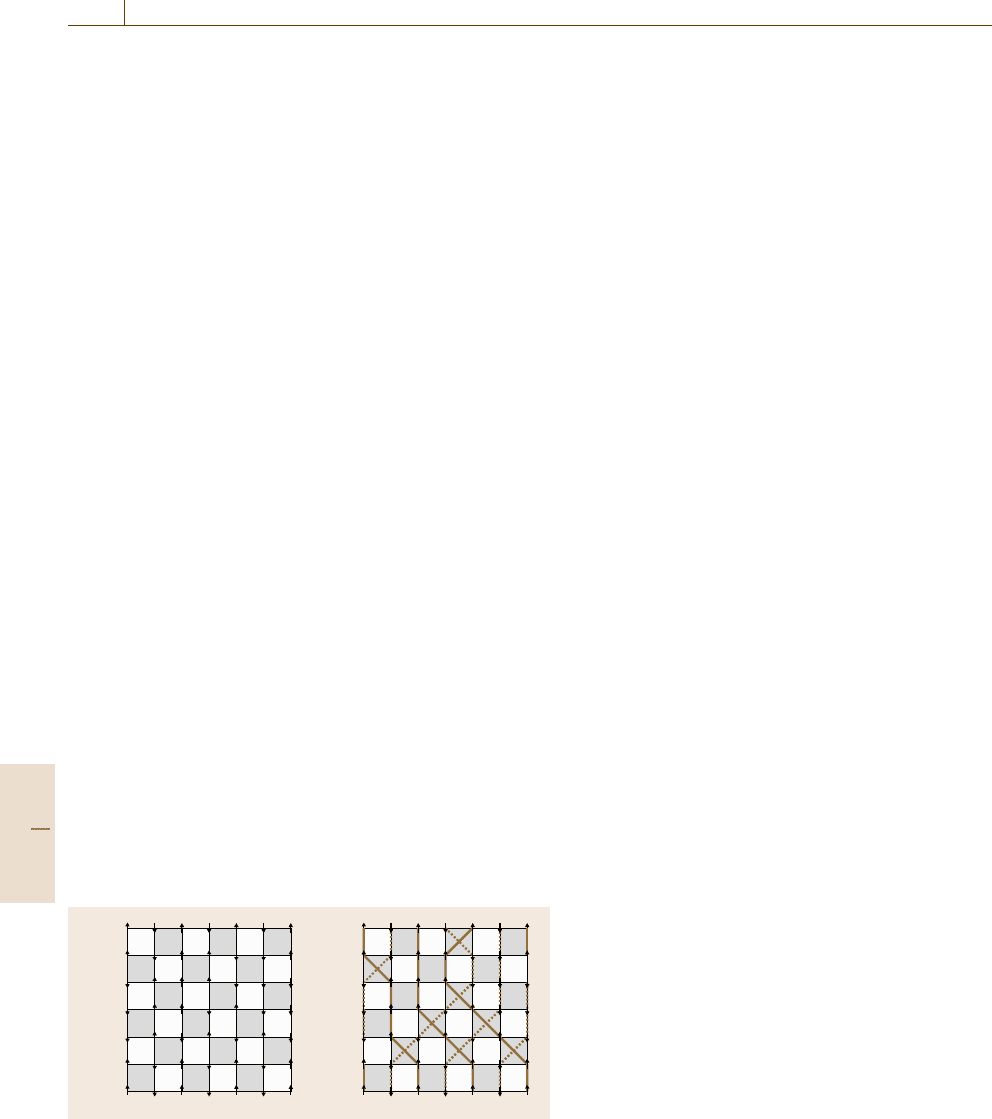
Fig. 22.4 (a) (d +1)-dimensional space-time for N

site quantum

system. (b) World-line conﬁguration. The vertical axis represents

the Trotter axis, and m is the Trotter number

the corresponding (d +1)-dimensional classical sys-

tems. The Suzuki–Trotter transformation is the most

typical procedure of this mapping using the Trotter for-

mula. In order to explain the basics of quantum Monte

Carlo methods, we review ﬁrst the Suzuki–Trotter for-

malism [22.53].

The partition function of quantum systems is gener-

ally deﬁned as

Z =Tr e

−βH

, (22.49)

where β and H are the inverse temperature and the

Hamiltonian, respectively. Using the generalized Trot-

ter formula, the exponential of quantum Hamiltonians

can be decomposed into the product of exponentials in

inﬁnitesimal time-slices as

βH

= lim

n→∞





−ΔτH



, (22.50)

where Δτ = β/n,andH

is a local Hamiltonian that

satisﬁes H =



. Inserting complete sets between

time slices, the partition function can be expressed in

terms of local weights as

Z =



W(A) , W(A) =



w(a

) . (22.51)

Here, A denotes a conﬁguration such as shown in

Fig. 22.4a, and a is a local conﬁguration on a plaquette.

Their weights are represented by W(A)andw(a), re-

spectively. Plaquette weights are deﬁned on shaded

plaquettes in Fig. 22.4a.

In this way, the system is mapped onto a (d +1)-

dimensional classical system. This transformation is

called the Suzuki–Trotter transformation [22.54, 55].

Quantum Monte Carlo simulations are performed

through updates of conﬁgurations in the (d +1)-

dimensional space-time. For recent progress see [22.56,

57].

22.3.2 World-Line Approach

In order to explain how quantum Monte Carlo simula-

tions are performed in the (d +1)-dimensional space-

time, we here review the world-line algorithm. As an

example, we consider the spin-1/2 Heisenberg model,

which is deﬁned by the following Hamiltonian

H = J



i, j

·S

, (22.52)

Part E 22.3

Monte Carlo Simulation 22.3 Quantum Monte Carlo Method 1127

where the summation is taken over nearest-neighbor

sites, and S

denotes the spin operator at site i. All the

possible local conﬁgurations and weights of plaquettes

in a time-slice are listed in Table 22.1.

Up spins (or down spins) may be joined by lines as

illustrated in Fig. 22.4b. These lines are called world-

lines [22.58]. In the world-line algorithm, world-line

conﬁgurations are updated. One way to update them is

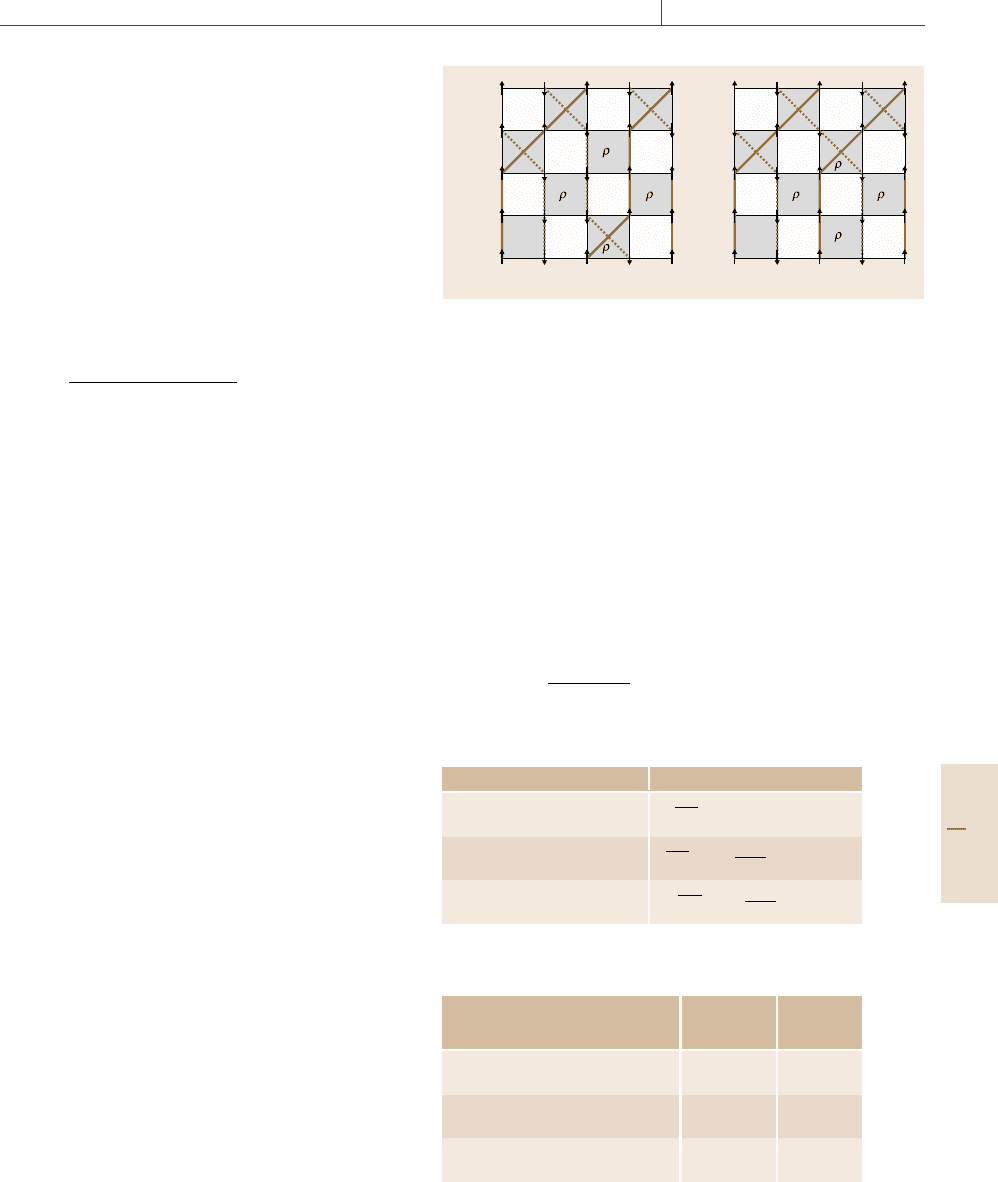
the following: As illustrated in Fig. 22.5,wetrytoﬂip

four spins (a, b, c, d), taking care so that the ﬂip satisﬁes

the conservation law of the model. The new world-line

conﬁguration is accepted with the probability

P =



+ρ



, (22.53)

based on the heat-bath algorithm (or the Metropolis al-

gorithm). In this way, world-lines are locally moved.

This process is called a local ﬂip. Since the ergodicity

is not satisﬁed by this type of updates only [22.59], we

need other types of ﬂips. If up spins (or down spins)

align in the imaginary time direction or in the diago-

nal directions, they can ﬂip simultaneously. If up and

down spins align alternately in the space direction, they

can also ﬂip simultaneously. These types of ﬂips are

called global ﬂips [22.60]. Combining these two types

of ﬂips, world-line conﬁgurations are updated. Phys-

ical quantities such as magnetization, susceptibilities,

energy and speciﬁc heat can be measured using spin

conﬁgurations, local weights and their derivatives in the

(d +1)-dimensional space-time [22.61–63].

In the world-line algorithm, the width of the time

slice is ﬁnite. Hence, the extrapolation Δτ →0 is nec-

essary after simulations. The error due to the ﬁnite Δτ

is systematic: It is proportional to Δτ

or Δτ

,etc.,de-

pending on the way of decomposition in (22.50) [22.64,

65]. In the continuous-time algorithm, the discreteness

of the Trotter slice is removed by taking Δτ → 0in

the deﬁnition of local probabilities as will be discussed

later.

22.3.3 Cluster Algorithm

Spin conﬁgurations in the (d +1)-dimensional space-

time can be updated more efﬁciently by using the

cluster algorithm. For the cluster algorithm in quan-

tum systems [22.35, 40], readers may refer to excellent

overviews in [22.66, 67]. In the cluster algorithm,

spin conﬁgurations as in Fig. 22.4a are mapped onto

graphs [22.68, 69]. The weights V(G)ofgraphG are

a b

(1)

1234(1)

(1)

1 2 3 4 (1)

Fig. 22.5a,b Local ﬂip in the world-line algorithm in a four-spin

system with the Trotter number m =4

deﬁned in order to satisfy the following relation

W(A) =



V(G)Δ(A, G) , (22.54)

where Δ(A, G) is one if spin conﬁguration A is com-

patible with graph G, and otherwise zero. Similarly, it

is possible to deﬁne the local version of (22.54)as

w(a) =



v(g)δ(a, g) . (22.55)

For the Heisenberg model deﬁned in (22.52), δ(a, g)is

chosen as shown in Table 22.2.

The probability P(g|a) of assigning graph g to con-

ﬁguration a is given by

P(g|a) =

δ(a, g)v(g)

w(a)

. (22.56)

Table 22.1 Local conﬁgurations and their weights

a w(a)



↑↑





↓↓



−

Δτ J



↑↓





↓↑



Δτ J

cosh



Δτ J





↑↓

↓↑





↓↑

↑↓



−e

Δτ J

sinh



Δτ J



Table 22.2 Function δ(a, g) for mapping of local conﬁgu-

rations to graphs



↑↑





↓↓



1 0



↑↓





↓↑



1 1



↑↓

↓↑





↓↑

↑↓



0 1

Part E 22.3