Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing

Подождите немного. Документ загружается.

1098 Part E Modeling and Simulation Methods

Step 5

is determined from a constraint condition for

the whole body.

Utilizing steps 1 to 5, we are able to evaluate the

elastic strain energy of the coherent two-phase micro-

structure. When we try to calculate the elastic strain

energy, it is important to distinguish the known vari-

ables and the unknown ones. In this case, the given

variable is ε

(r) that is calculated directly from the

composition ﬁeld c(r), and the unknown variable is

(r). The following formulation of elastic strain en-

ergy may look complicated, but the basic idea is simple.

We evaluate the unknown variable using the known one

through the mechanical equilibrium equation and the

boundary conditions. Detail of the evaluation method

is explained along the lines of step 1 to 5 as follows.

Step 1

When the lattice parameter a is a linear function of

the composition, i. e., the Vegard’s law is satisﬁed, a is

given by

a(r) =a

c(r) , (21.28)

where c(r) is a local solute composition of component B

at position r,anda

is the lattice parameter for pure

A component. In this case, the eigenstrain is deﬁned by

(r) ≡

a(r) −a

=ηc(r)δ

η ≡

, (21.29)

where η is a lattice mismatch that is calculated from the

lattice parameters of pure A and B metals. Since the lat-

tice parameters of pure component and the composition

ﬁeld c(r) are given in advance, the spatial distribution

of the eigenstrain ε

(r) in the microstructure is easily

calculated from (21.29).

Step 2

Next, the total strain ε

(r)isdeﬁnedby

(r) ≡

+δε

(r) , (21.30)



δε

(r)dr =0 , (21.31)

where

is a volume average of ε

(r), δε

(r)isthe

deviation from

, and is deﬁned using the displacement

vector u

(r)as

δε

(r) ≡



∂u

(r)

∂r

∂u

(r)

∂r



. (21.32)

The elastic strain ε

(r)isdeﬁnedby

(r) ≡ε

(r)−ε

(r) . (21.33)

On the basis of the linear elasticity theory, the stress is

evaluated based on Hook’s law

(r) =C

ijkl

(r) =C

ijkl



(r) −ε

(r)



(21.34)

where C

ijkl

is an elastic constant.

Step 3

The mechanical equilibrium equation is expressed as

, j(r) =

∂σ

(r)

∂r

=0 , (21.35)

where the no body force condition is assumed. Substi-

tuting (21.29), (21.32), and (21.34)into(21.35) yields

ijkl

∂

∂r

ijkl

ηδ

∂c

∂r

. (21.36)

The functions c(r), u

and δε

(r) are expressed in the

form of a Fourier integral as follows

c(r) =



c(k) exp(ik·r)

(2π)

(21.37)

(r) =



(k) exp(ik·r)

(2π)

(21.38)

δε

(r) =



(k) exp(ik·r)

(2π)

, (21.39)

where k =(k

, k

) is a reciprocal wave vector in

Fourier space. Substituting (21.37–21.39)into(21.36)

and focusing on the amplitude part of the Fourier ex-

pression, we obtain

ijkl

(k) =−iC

ijkl

ηδ

c(k) . (21.40)

This is a Fourier expression of the mechanical equilib-

rium equation. (Note that the upright i is the imaginary

number, not an index for vector or tensor.) Here, we

deﬁne the following equations

−1

(k) ≡C

ijkl

, (21.41)

≡C

ijkl

ηδ

. (21.42)

Using (21.41)and(21.42)in(21.40), the

(k), that is

a Fourier transform of u

(r), is given by

(k) =−iG

(k)C

ijkl

ηδ

c(k)

=−iG

(k)σ

c(k) . (21.43)

Part E 21.2

Phase Field Approach 21.2 Total Free Energy of Microstructure 1099

Since the Fourier transform of (21.32)is

(k) =i



(k)k

, (21.44)

substituting (21.43)into(21.44) yields

(k) =i



(k)k

=−iiG

(k)k

c(k)

= G

(k)k

ijmn

ηδ

c(k) . (21.45)

The values of the elastic constant C

ijkl

and the lattice

mismatch η are given from the materials parameters

in advance. Since the composition ﬁeld c(r)isgiven

beforehand,

c(k) is calculated by the ﬁrst Fourier trans-

form of c(r) numerically. Therefore, δ

(k) is directly

calculated based on (21.45) and obtained as a function

of k,thenδε

(r) is calculated through the inverse ﬁrst

Fourier transform of δ

(k) numerically.

Step 4

The elastic strain energy is given as

str



ijkl

(r)ε

(r)dr



ijkl



+δε

(r) −ε

(r)





+δε

(r) −ε

(r)

dr ,

(21.46)

where the elastic strain is deﬁned by

(r) ≡ε

(r)−ε

(r)

+δε

(r) −ε

(r) (21.47)

and we are able to rewrite (21.46) using (21.47)as

str



ijkl



+δε

(r) −ε

(r)





+δε

(r) −ε

(r)



ijkl

dr +

ijkl



δε

(r)dr

−

ijkl



(r)dr

ijkl



δε

(r)dr



ijkl

δε

(r)δε

(r)dr

−

ijkl



δε

(r)ε

(r)dr

−

ijkl



(r)dr

−



ijkl

(r)δε

(r)dr



ijkl

(r)ε

(r)dr

ijkl



dr −C

ijkl



(r)dr

ijkl



(r)ε

(r)dr

−C

ijkl



δε

(r)ε

(r)dr



ijkl

δε

(r)δε

(r)dr

ijkl

−C

ijkl



c(r)dr

ijkl



{c(r)}

−

ijkl



δε

(r)ε

(r)dr

ijkl

−C

ijkl

ηc

ijkl

{c(r)}

−



(n)σ



c(k)



(2π)

(21.48)

Part E 21.2

1100 Part E Modeling and Simulation Methods

where n is a unit vector in the k direction, n ≡k/|k|,and

−1

(n) ≡C

ijkl

. The following equations



δε

(r)dr =0 ,



(r)dr =δ



c(r)dr =δ

ηc



ijkl

δε

(r)ε

(r)dr =



ijkl

δε

(r)δε

(r)dr ,

are used for formulation of (21.48). The last relation of

the above equations is obtained as follows



δσ

(r)u

(r)n

dS −



δσ

ij, j

(r)u

(r)dr = 0 ,



∵ δσ

(r)n

=0 ,δσ

ij, j

(r) =0





δσ

(r)δε

(r)dr = 0 ,



ijkl

δε

(r)



δε

(r) −ε

(r)



dr = 0 ,

∴



ijkl

δε

(r)ε

(r)dr =



ijkl

δε

(r)δε

(r)dr ,

where δσ

(r) =C

ijkl



δε

(r)−ε

(r)



and the Gauss in-

tegral is used. Furthermore, the mechanical equilibrium

equation and the force balance at the body surface, i. e.,

the pressure on the surface is assumed to be 0, are con-

sidered.

Step 5

In the ﬁnal stage of evaluating the elastic strain energy,

the average value of the total strain

is determined.

is commonly evaluated by one of the following four

types of boundary conditions.

1. The surface of the body is rigidly constrained and

there is no external stress ﬁeld.

Since the surface is ﬁxed, the average of the total

strain should be 0, i. e.,

=0 . (21.49)

2. The body is constrained under homogeneous exter-

nal strain

In this case, the average total strain is the same as

,i.e.,

, (21.50)

where the

is a known variable given by the

boundary condition.

3. The surface of the body is unﬁxed and there is no

external stress.

In this case, since the object can be expanded or con-

tracted freely, the average total strain under a stable

state should satisfy the condition

∂E

str

∂

=0 . (21.51)

Substituting (21.48)into(21.51), we obtain the fol-

lowing relation

∂E

str

∂

ijkl

−C

ijkl

ηc

=0 ,

∴

=δ

ηc

. (21.52)

4. The surface of the body is unﬁxed and the external

stress σ

is applied.

In this case, the Gibbs energy is given as

G = E

str

−σ

. (21.53)

Since the average of total strain under the stable

state should satisfy the condition

∂G

∂

=0 , (21.54)

substituting (21.53)and(21.48)into(21.54) yields

∂G

∂

ijkl

−C

ijkl

ηc

−σ

=0 ,

∴

−1

ijkl

+δ

ηc

, (21.55)

where C

−1

ijkl

is an elastic compliance, i. e., an inverse

matrix of C

ijkl

It is worth noting that the elastic strain is expressed

using (21.52)as

(r) =ε

(r) −ε

(r)

+δε

(r) −ηδ

c(r)

=δ

ηc

+δε

(r) −ηδ

c(r)

=δε

(r) −ηδ

[

c(r) −c

]

. (21.56)

This equation means that the phrases the mechan-

ical equilibrium condition of the uniform strain

is considered and the eigenstrain is redeﬁned as

(r) ≡ηδ

[

c(r) −c

]

are equivalent.

As for the multicomponent and multiphase system,

the eigenstrain is expressed as a linear function of

the order parameters φ

(r, t) =



(p) φ

(r, t) , (21.57)

Part E 21.2

Phase Field Approach 21.2 Total Free Energy of Microstructure 1101

where φ

corresponds to the composition ﬁeld c and

the squire of crystal structure ﬁeld s

. ε

(p) is a lat-

tice mismatch concerning the order parameter φ

The derivation of elastic strain energy in this case is

straightforward.

The evaluation of E

str

mentioned above is for the homo-

geneous case, i. e., the elastic constant does not depend

on the local order parameter. The elastic strain energy

calculation in inhomogeneous case has been proposed

and discussed in [21.39,40].

21.2.4 Free Energy for Ferromagnetic

and Ferroelectric Phase Transition

The order parameter used to describe ferromagnetic

phase transition is a magnetization moment M,and

the polarization moment P is employed as an order

parameter for representing the ferroelectric phase tran-

sition in dielectric materials. In order to describe the

ferromagnetic or ferroelectric domain microstructure

formation in the phase-ﬁeld method, the order param-

eters, M and P, are deﬁned as a function of position r

and time t.

Since a description of the energy for the ferro-

magnetic and ferroelectric phase transition has a quite

similar formulation, we explain the total free energy de-

scription for a ferroelectric phase transition during the

structural phase transformation from cubic to tetragonal

along the line of Wang’s analysis [21.20].

In this ﬁeld, the Landau-type bulk free energy den-

sity is commonly expressed by a six-order polynomial

of the spontaneous polarization

=α





+α



+ P



+α





+α





+α







+ P











+α

, (21.58)

where three variants are considered, and α

are constant

coefﬁcients. The subscripts i = 1, 2, and 3; indicate

a variant number. In the Ginzburg–Landau theory, the

free energy function also depends on the gradient of

the order parameter (that is, corresponding to the gradi-

ent energy). For ferroelectric materials, the polarization

gradient energy represents the ferroelectric domain wall

energy. For simplicity, the lowest order of the gradient

energy density takes the form

grad



1,1

2,2

+ P

3,3



+κ



1,1

2,2

+ P

2,2

3,3

+ P

3,3

1,1







1,2

+ P

2,1





2,3

+ P

3,2





1,3

3,1









1,2

− P

2,1





2,3

− P

3,2





1,3

−P

3,1





, (21.59)

where κ

are gradient energy coefﬁcients and P

i, j

denotes the derivative of the ith component of the po-

larization vector P

with respect to the jth coordinate.

In the phase-ﬁeld simulations, each element is rep-

resented by an electric dipole with its strength of the

dipole being given by a local polarization vector P

The multiple dipole–dipole electric interactions play

a crucial role in calculating the morphology of a do-

main structure and in the process of domain switching

as well. The multiple dipole–dipole electric interaction

energy density is calculated by

(r) =−

dip

(r) · P(r) , (21.60)

where

dip

(r) =−

4πε





P(r



)

r −r



−

3(r −r



)P(r



)·(r −r



)

r −r



(21.61)

is the electric ﬁeld at point r induced by all dipoles.

When there is an externally applied electric ﬁeld E

an additional electrical energy

=−E

(21.62)

should be taken into account in the simulations. The

spontaneous strains are associated with spontaneous

polarizations. The eigenstrains are linked to the polar-

ization components in the following form

= Q





= Q





= Q





=ε

= Q

=ε

= Q

=ε

= Q

, (21.63)

Part E 21.2

1102 Part E Modeling and Simulation Methods

where Q

are the electrostrictive coefﬁcients. When

a dipole is among other dipoles with different ori-

entations, there exist multiple dipole–dipole elastic

interactions. The multiple dipole–dipole elastic inter-

actions play an essential role in the determination of

a domain structure. A twin-like domain structure is

formed when the multiple dipole–dipole elastic inter-

actions predominate.

Due to the constraint of the surroundings, the

polarization-related strains include two parts: the elas-

tic strain and the eigenstrain. The elastic strain related

to polarization and/or polarization switching is given by

=ε

−ε

. (21.64)

When there exists an externally applied homogeneous

stress σ

, using the superposition principle, we have the

total elastic strains of the system

=ε

−ε

ijkl

, (21.65)

where S

ijkl

is the elastic compliance matrix. Finally, the

elastic strain energy density under the cubic approxima-

tionisgivenby

str



















+ε



+2C

















. (21.66)

As described above, the elastic strain energy is a func-

tion of polarization and applied stresses. An applied

electric ﬁeld can change the polarization and conse-

quently vary the elastic strain energy density. On the

other hand, an applied stress ﬁeld can also change the

polarization and thus change the electric energy density.

Integrating the free energy density over the entire

volume of a simulated ferroelectric material yields the

total free energy, F

ele

, under externally applied electri-

cal and mechanical loads, E

and σ

. Mathematically,

we have

ele





) + f

grad

i, j

) +e

str



,σ



) + f



, E





dr .

(21.67)

As for the energy description for a ferromagnetic phase

transition, the order parameter is changed from P to M.

The bulk Landau free energy density, in this case, cor-

responds the magnetocrystalline anisotropy energy. The

formulation of another parts is almost the same and

straightforward.

21.3 Solidiﬁcation

21.3.1 Pure Metal

The interface between a liquid phase and a solid one

is expressed by the continuum scalar function φ,which

is called a phase-ﬁeld variable and takes values from

0 (liquid phase) to 1 (solid phase) as illustrated in

Fig. 21.1. The variable φ is a function of spatial posi-

tion r =(x, y, z) and time t, and then the solidiﬁcation

process is represented by a temporal development of

the φ ﬁeld. Indicating the interface using φ, we are

able to treat the complex changes of interface shapes

such as a dendrite. The conditions of the interface

curvature and temperature distribution around the in-

terface are automatically satisﬁed by employing the

parameters obtained from the physical properties at the

interface.

The total free energy of the pure metal during solid-

iﬁcation is given by

F =





f (φ, T ) +

∇φ



dV , (21.68)

where f (φ, T ) is a chemical free energy deﬁned by

f (φ, T ) ≡h(φ) f

(T )+[1−h(φ)] f

(T )+Wg(φ) .

(21.69)

Functions f

(T )and f

(T ) are the chemical free en-

ergy for the solid and the liquid phase, respectively,

given as a function of temperature T. The function h(φ)

is a monotonic increasing function satisfying the con-

straint h(0) =0andh(1) =1. The product Wg(φ)inthe

right-hand side of (21.69) is the energy barrier term,

which takes a maximum value W within 0 <φ<1and

g(0) =g(1) =0, and is introduced in order to not mix

the solid and liquid phases. The second term inside the

integral of the right-hand side in (21.68) is a gradient

energy that corresponds to the interfacial energy, and

is the gradient energy coefﬁcient. When orientation

dependence on the interfacial energy is considered, ε is

assumed as a function of orientation.

In the phase-ﬁeld method, the temporal and spatial

development of the φ ﬁeld is assumed to be proportional

Part E 21.3

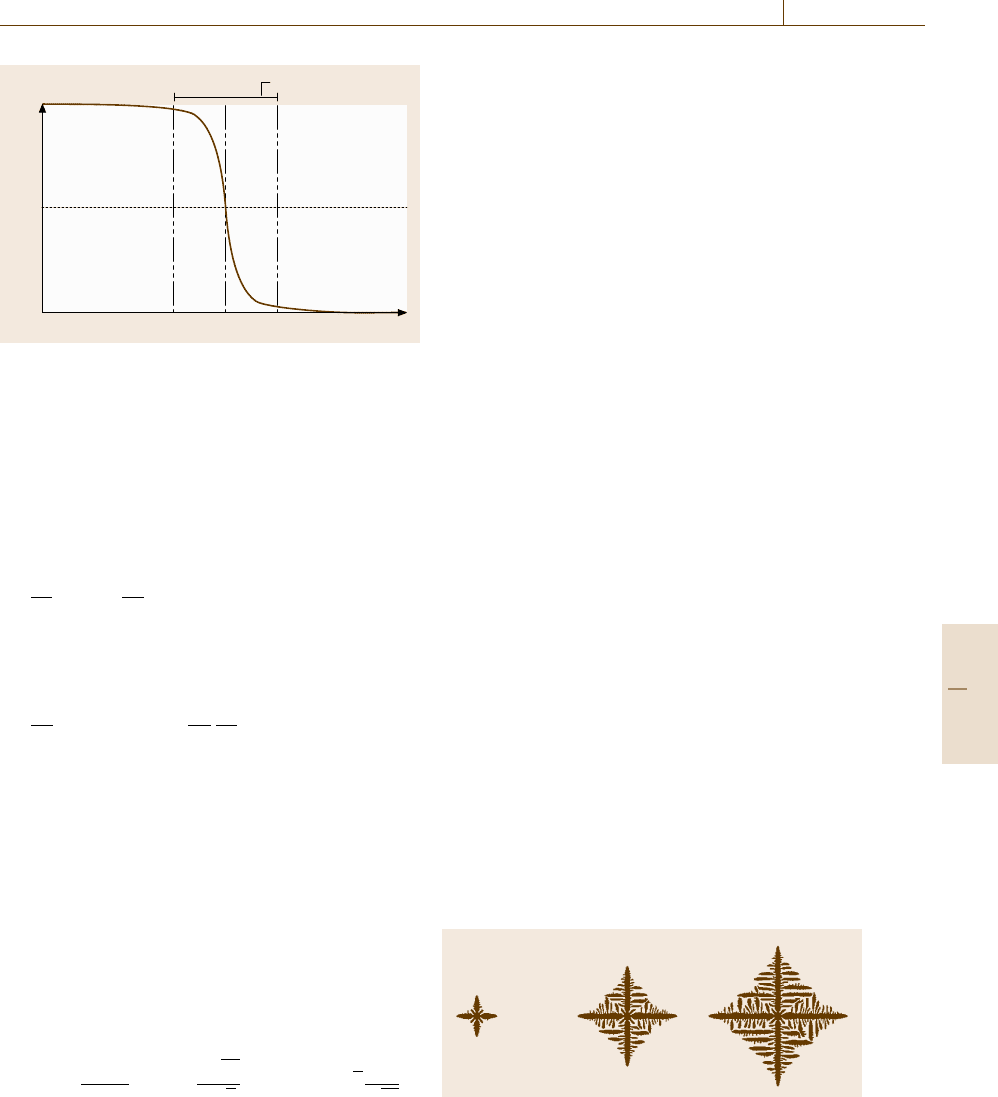
Phase Field Approach 21.3 Solidiﬁcation 1103

0.5

Solid phase Liquid phase

2λ

Distance x

Phase-field φ

Interface region

Fig. 21.1 Schematic illustration of the one-dimensional

proﬁle of phase-ﬁeld order parameter φ across the inter-

face. The variable φ is commonly deﬁned as a function of

spatial position r and time t, and the ﬁeld dynamics, such

as a solidiﬁcation process, is represented by a temporal

development of the ﬁeld φ(r, t)

to the variation of the total free energy F with respect

to φ, therefore the following differential evolution equa-

tion

∂φ

∂t

=−M

δF

δφ

, (21.70)

is employed, where M

is a mobility of the interface

motion. As for the temporal and spatial changes of

a temperature ﬁeld, the thermal diffusion equation

∂T

∂t

= D∇

T − p(φ)

∂φ

∂t

(21.71)

is applied. The second term of the right-hand side of

(21.71) means the diverging term of heat produced from

latent heat during solidiﬁcation. Symbols D, L,andC

are thermal diffusivity, latent heat, and speciﬁc heat,

respectively. A function p(φ) satisﬁes the conditions



p(φ)dφ =1andp(0) = p(1) =0, which is often de-

ﬁned by p(φ) ≡ ∂h/∂φ using the function h(φ). The

phase-ﬁeld method for the solidiﬁcation simulation in

a pure metal is calculated based on (21.70)and(21.71).

The parameters M

, W,andε are determined from

the interface thickness 2λ (Fig. 21.1) and the interfa-

cial energy density σ . The relations between them are

summarized as

μσ

,σ=

√

, 2λ =2.2

√

(21.72)

is the melting temperature, and μ is the kinetic co-

efﬁcient determined by v

/μ = f

− f

−2σ/R that

is an equation of the sharp interface motion, where

and R are an interface velocity and a curvature

at the interface. The numerical technique to solve the

nonlinear differential equations is commonly a ﬁnite

difference simulation. Since the calculation method is

mathematically equivalent to that solving the differen-

tial equation describing temporal ﬁeld dynamics, we

can utilize many techniques developed in the ﬁeld of

the computational ﬂuid dynamics.

The result of a two-dimensional simulation of den-

drite growth in pure metal is shown in Fig. 21.2. The

black and white parts are the solid and liquid phase, re-

spectively. Note that the complex morphological change

of the realistic dendrite growth is quite reasonably

calculated.

Since the width of the solid–liquid interface in

the solidiﬁcation process commonly has the length

of an atomic scale, the temperature ﬁeld causes nu-

merical errors in the gradual interface as shown in

Fig. 21.1, if the numerical difference calculation is per-

formed using coarse difference dividing cells. Since

the parameter M is derived assuming the temperature

is constant within the interface, a small calculation

mesh size is required to neglect the temperature change

though the interface region in the numerical simula-

tion. Hence, the interface width should be negligibly

small as compared to the capillary length and the-

oretically at the sharp interface limit. However, the

value of the interface width is sometimes selected

as large beyond the restriction for the computational

efﬁciency.

This made the limit of the phase-ﬁeld method at an

early stage when this simulation method was proposed,

but the new technique (called the thin interface limit

model) of amending the point mentioned above has

already been proposed. For example, Karma and Rap-

pel [21.10] derived the phase-ﬁeld mobility in the thin

interface limit to relax the restriction of the interface

a) b) c)

Fig. 21.2a–c Two-dimensional phase-ﬁeld simulation of

a dendrite growth process in pure metal is represented from

(a)–(c).Theblack and white parts represent a solid and

liquid phase, respectively

Part E 21.3

1104 Part E Modeling and Simulation Methods

width and expressed it as follows

−1



δL

4DC



−1

K =



h(φ)

[

1 −h(φ)

]

φ(1 −φ)

dφ. (21.73)

This thin interface limit model not only improves com-

puter efﬁciency but also removes the limitation for the

kinetic coefﬁcient. They showed that the numerical cal-

culation of the dendrite shape using the phase-ﬁeld

model agreed well with the solvability theory in both

2-D and 3-D. Therefore, we should emphasize that

the idea that the phase-ﬁeld method always physically

requires a smooth interface is a mistake, and the phase-

ﬁeld method can be applied to the sharp interface with

one atomic layer.

21.3.2 Alloy

In the phase-ﬁeld model for alloy solidiﬁcation, the lo-

cal solute composition c is also employed as one of

the phase-ﬁeld order parameters and the gradient en-

ergy term for the solute composition ﬁeld is introduced

into the total free energy functional. But when the inter-

face region is small relative to the entire microstructure

simulated, a similar problem explained for the tempera-

ture ﬁeld in the above section arises for the composition

ﬁeld. The thin interface model considering the compo-

sition ﬁeld was proposed by Kim et al. [21.11]. They

deﬁned the interface as a fraction weighted mixture of

the solid and liquid with different compositions and free

energy, where the compositions of solid and liquid at

the interface are determined to have the same chem-

ical potential μ, i. e., the local equilibrium is assumed

to be

(T ) +(1 −c

) f

(T ) ,

(T )+(1 −c

) f

(T ) ,

c = h(φ)c

+[1 −h(φ)] c

) =μ

) . (21.74)

The local solute composition of the solid phase

and the liquid one is denoted by c

and c

, re-

spectively. This model is called the KKS model

(Kim–Kim–Suzuki model) [21.11], where a so-

lute diffusion equation is solved simultaneously

∂c

∂t

=∇·



(φ)

∇ f



, (21.75)

a) b)

Fig. 21.3a,b The change in dendrite shape of steel due

to a ternary alloying element is demonstrated for (a) Fe-

0.5 mol % C; and (b) Fe-0.5mol%C-0.001 mol % P (af-

ter [21.12]). The simulation results show that a small

addition of phosphorus changes the secondary arm spacing

signiﬁcantly even when it does not signiﬁcantly change the

interface velocity

where D

is the solute diffusivity and f

and f

are the ﬁrst and the second derivatives of the chem-

ical free energy density. The parameters, ε and W,

are the same as the ones in the pure material solid-

iﬁcation case deﬁned by (21.72). The mobility M in

the thin interface limit was also derived by Kim et al.

−1



1 −k

√



, c







, c



= f









−c





h(φ)

[

1−h(φ)

]

[1−h(φ)] f





+h(φ) f





φ(1 −φ)

dφ,

(21.76)

where D

is a diffusion coefﬁcient of liquid phase,

and m

are a partition coefﬁcient and a gradient of

liquidus line on the corresponding phase diagram, re-

spectively. V

is a molar volume and the superscript e

indicates that the parameter is in a local equilibrium

state.

The phase-ﬁeld simulation of the dendrite shape

changes performed by Suzuki et al. for Fe-0.5mol%C

binary alloy and Fe-0.5mol%C-0.001 mol % P ternary

alloy at 1780 K is shown in Fig. 21.3 [21.12]. The

secondary arms develop well and the arm spacing

becomes narrow with a small addition of phospho-

rous because the phosphorous is likely to enrich the

interface and reduce the interface stability. The simu-

lation results show that a small addition of phosphorus

changes the secondary arm spacing signiﬁcantly even

when it does not signiﬁcantly change the interface

velocity.

Part E 21.3

Phase Field Approach 21.4 Diffusion-Controlled Phase Transformation 1105

21.4 Diffusion-Controlled Phase Transformation

21.4.1 Cahn–Hilliard Diffusion Equation

Since the relation between the kinetics and the ther-

modynamics of phase transformations is plainly formu-

lated in the diffusion theory treating an interdiffusion,

the diffusion controlled phase decomposition in solid–

solid phase transformations is a very good example for

explaining the relation between energetics and dynam-

ics in microstructure evolution. In this section, the basis

of the diffusion equation concerning phase decomposi-

tion is explained [21.41].

From a physical viewpoint, atom diffusion in solids

is formulated based on the equation of the friction.

Because the diffusion of the atom inside the solid corre-

sponds to the movement of the object in the medium

with a very strong viscosity, the inertia term in the

equation of motion (the so-called Ranjuban equation)

attenuates exponentially and only the friction term will

remain. We consider the case where atom A moves with

speed v

and a thermodynamic driving force to move

this atom is assumed to be F

. The F

is deﬁned by

=−∇μ

, (21.77)

where μ

is the chemical potential of component A.

Thus, the velocity of atom A, v

, is given by the equa-

tion of the friction

= M

=−M

∇μ

, (21.78)

where M

is the mobility for atom A diffusion, which is

a parameter indicating the easiness of atom movement

and is physically equivalent to the reciprocal of the fric-

tion coefﬁcient. M

is, exactly, a function of the local

composition around the atom A in diffusing, but it is of-

ten assumed to be constant for simplicity. Using (21.78),

we obtain the diffusion ﬂow of component A, J

,which

is induced by a driving force F

,as

=−M

∇μ

, (21.79)

where c

is a local composition of component A.

Next, we derive the equation of interdiffusion for

the diffusion couple of A–B binary system. Henceforth,

the element names A and B are referred to as 1 and 2,

respectively, at the symbol subscript. The equation de-

scribing the interdiffusion is derived by eliminating v

in the right-hand side of the following equations, which

are the governing equations for a macroscopic ﬂux ﬂow

of the solute element

=−c

∇μ

=−c

∇μ

, (21.80)

where v

is a macroscopic ﬂux ﬂow of the so-

lute element, for instance, in the diffusion couple, it

corresponds to the macroscopic velocity of coupling in-

terface. According to the conservation law, the diffusion

equation is deﬁned as

∂c

∂t

=−∇· J

=∇·

(

∇μ

−v

)

∂c

∂t

=−∇· J

=∇·

(

∇μ

−v

)

. (21.81)

Therefore, the relation

∂(c

)

∂t

=∇·(c

∇μ

−v

) =0

∴ c

∇μ

−v

=C : const

is obtained by considering c

=1. Furthermore, if

we assume ∇μ

= 0, ∇μ

= 0andv

= 0 at the po-

sition far from the coupling interface, the value of C

should be 0. Because C is a constant and independent

of position. Therefore, the velocity of the coupling in-

terface is given by

∇μ

. (21.82)

Substituting (21.82)into(21.81), we obtain the interdif-

fusion equation as a form of

=−(c

∇μ

=−(c

∇(μ

−μ

)

=−(c

∇



∂g

∂c



=−(c



∂

∂c



∇c

=−(c

∇μ

=−(c

∇(μ

−μ

)

=−(c

∇



∂g

∂c



=−(c



∂

∂c



∇c

. (21.83)

In the formulation of (21.83), the Gibbs–Duhem rela-

tions

dμ

=0 ,

→ c

dμ

−c

dμ

∴ dμ

d(μ

−μ

)

Part E 21.4

1106 Part E Modeling and Simulation Methods

and

∂g

∂c

=μ

−μ

∂μ

∂c

∂μ

∂c

=μ

−μ

∂g

∂c

=μ

−μ

are used, where g

is a chemical free energy density.

According to (21.83), the interdiffusion coefﬁcient is

expressed as follows

=(c



∂

∂c



=(c



∂

∂c



. (21.84)

In particular, when g

is a chemical free energy

for an ideal solid solution, we ﬁnd the relation

∂

/∂c

= ∂

/∂c

= RT/(c

) and entering this

into (21.84), we have

RT +c

RT = c

∗

(21.85)

where D

∗

= M

RT and D

∗

= M

RT are the Einstein’s

relations, R is the gas constant and T is the absolute

temperature, and D

∗

is a self-diffusion coefﬁcient.

On the other hand, the phenomenological equation

for the generalized Fick’s ﬁrst law is deﬁned as

=−L

∇μ

−L

∇μ

=−L

∇μ

−L

∇μ

, (21.86)

where L

is the Onsager coefﬁcient, which should sat-

isfy the relation

=0 , L

= L

(21.87)

The above relation is derived from the restriction of

solute conservation law and the condition of the de-

tailed balance of local equilibrium. Considering (21.87)

in (21.86), we get

=−L

∇(μ

−μ

) ,

=−L

∇(μ

−μ

) . (21.88)

Since (21.83)and(21.88) should be the same equation,

the Onsager coefﬁcient is given by

= L

=(c

= L

=0 . (21.89)

An important point is that the interdiffusion and

Onsager coefﬁcients are obtained using (21.84)and

(21.85), if a self-diffusion coefﬁcient and a chemical

free energy function g

are experimentally determined.

Although we considered the chemical free energy g

in the formulation mentioned above, the more general

evolution equation that is able to describe the mi-

crostructure changes in the diffusion controlled phase

transformation can be deduced using the total free en-

ergy of the microstructure G

sys

instead of the chemical

free energy g

. For instance, the diffusion ﬂux J

expressed as

=−(c

∇

δG

sys

δc

. (21.90)

By comparing (21.83)and(21.90), the mobility M

should be written as

) =(c

. (21.91)

Therefore, the nonlinear diffusion equation describing

diffusion-controlled phase transformations is given as

∂c

∂t

=∇·



)∇

δG

sys

δc



, (21.92)

where the composition ﬂuctuation term (i. e., the ran-

dom noise term) is ignored.

This equation is a general form for the diffusion

equation, and the Cahn–Hilliard equation [21.29] is also

constructed from this equation. In the spinodal theory,

the total free energy G

sys

of the phase decomposed in-

homogeneous microstructure is expressed as

sys





(c)+η

hkl

(c −c

)

+κ



∂c

∂x





dx ,

(21.93)

where the one-dimensional system (the one-dimensional

spatial direction is denoted by x with a total length L)

is considered for simplicity, and c is a local solute com-

position of element B in an A–B binary alloy system.

The quantities η, Y

hkl

,andκ are the lattice mismatch,

the function of the elastic constants, and the composi-

tion gradient energy coefﬁcient, respectively. The ﬁrst,

second, and third terms in the integral at the right-hand

side of (21.93) correspond to a chemical free energy,

an elastic strain energy, and a composition gradient en-

ergy, respectively. If F is deﬁned by the sum of these

three terms and the variation principle is applied to F

Part E 21.4

Phase Field Approach 21.4 Diffusion-Controlled Phase Transformation 1107

with respect to the invariant variables c, x,and(∂c/∂x),

the variation δG

sys

/δc is given as

δG

sys

δc

∂F

∂c

−



∂F

∂(∂c/∂x)



∂g

(c)

∂c

+2η

hkl

(c −c

) −2κ



∂

∂x



(21.94)

where the Euler equation is considered. δG

sys

/δc is

commonly called as a diffusion potential. Substituting

(21.94)into(21.92), we obtain the nonlinear diffusion

equation

∂c

∂t

∂

∂x





∂c

∂x



−2

∂

∂x





∂

∂x



, (21.95)

where

D ≡ M

(c)



∂

(c)

∂c

+2η

hkl



K ≡ M

(c)κ . (21.96)

In many textbooks of spinodal decomposition, M

is assumed to be a constant and

K has been moved out

beside the differentiation in the second term at the right-

hand side in (21.95). The value

D,deﬁnedby(21.96), is

then the interdiffusion coefﬁcient for the coherent phase

decomposition.

In the practical viewpoint for the actual numerical

simulation, it is effective to directly solve the equation

∂c

∂t

∂

∂x





∂μ

sys

∂x



(21.97)

instead of (21.95). In order to solve (21.97), the dif-

fusion potential μ

sys

≡ δG

sys

/δc is ﬁrst calculated as

a function of local position x and time t,andthen

(21.97) is solved using a numerical simulation tech-

nique such as a ﬁnite difference method.

21.4.2 Spinodal Decomposition

and Ostwald Ripening

Two-dimensional simulation of the spinodal decompo-

sition in the Fe-40 at. % Mo alloy within bcc crystal

structure during isothermal aging at 773 K is repre-

sented in Fig. 21.4 [21.14], where the Mo composition

is indicated using grayscale, i. e., the black part corres-

ponds to the Mo-rich region. The phase decomposition

is clearly recognized to progress with aging. The lat-

tice mismatch of the Fe-Mo alloy system is so large

20 nm

a) 0s' b) 30s' c) 50s'

d) 250 s' e) 500s' f) 1ks'

Fig. 21.4a–f Two-dimensional simulation of the spinodal decom-

position in the Fe-40 at. % Mo binary alloy with bcc crystal structure

during isothermal aging at 773 K, where the Mo composition is in-

dicated by gray scale,i.e.,theblack part corresponds the Mo rich

region. The lattice mismatch of the Fe-Mo alloy system is so large

that a modulated structure, i. e., the microstructure with ﬁne Mo-

rich zones along the 100directions, is produced by the mechanism

of spinodal decomposition. Numerical values in the ﬁgure are the

dimensionless aging time

20nm

t = 40s'

t = 60s'

t = 800 s'

t = 200 s'

Fig. 21.5 Three-dimensional phase ﬁeld simulation for the spinodal

decomposition of Fe-40 at. % Cr binary alloy at 773 K. The symbol t

is a dimensionless normalized aging time. The precipitate phase is

represented by an isocomposition surface of 40 at. %Cr

Part E 21.4