Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing

Подождите немного. Документ загружается.

1068 Part E Modeling and Simulation Methods

selected. The bcc-andfcc-based ordered phases are in-

cluded in the calculations. As can be seen in this table,

the calculated values and evaluated data are reasonably

consistent, and this close agreement encourages us to

proceed to the next step to evaluate the Gibbs free ener-

gies of solution phases.

First-principles Calculations

of the Gibbs Free Energy

The bcc phase in the Fe

−

Be binary system is illustrated

as an example to derive the Gibbs energy on the ba-

sis of ab initio method, since the phase is metastable

and located in the central part of the phase diagram, the

thermodynamic properties in this region are unknown.

An outline for deriving the Gibbs free energies of

the bcc-based structures incorporating the ab initio cal-

culations is as follows. First, a set of superstructures

{A-A2, A

B–D0

, AB-B2, AB-B32, AB

–D0

,B-A2}

are selected to be representative of a series of bcc-based

ordered phases, the total energies were calculated us-

ing the FLAPW method. With the known total energies,

the formation energy of the bcc-based superstructures,

ΔE

form

, is deﬁned by averaging the total energy of the

elements with chemical composition to the segregation

limit, as shown in the following equation

ΔE

form

(V) = E

tot

(V ) −



1−x



bccFe

tot

)

−x

bccBe

tot

) , (20.25)

Table 20.3 The values of ξ

for the bcc superstructures {A-A2, A

B–D0

, AB-B2, AB-B32, AB

–D0

,B-A2}

Ordered structures ξ

point ξ

n.n.pair ξ

n.n.n.pair ξ

triangle ξ

tetrahedron

A-bcc 1 1 1 1 1 1

B–D0

1 1/2 0 −1 −1 −1

AB-B2 1 0 −1 1 −1 1

AB-B32 1 0 0 −1 0 1

–D0

1 −1/2 0 −1 1 −1

B-bcc 1 −1 1 1 −1 1

Table 20.4 The formation energies to the segregation limit for the Fe

−

Be binary system in the D0

, B2, B32, and A2

structures in the ground state

Basic lattice Composition of Be Structure Formation enthalpy (kJ/mol)

bcc 0 Fe A2 0.0

bcc 0.25 Fe

Be D0

−12.3

bcc 0.5 FeBe B2 −31.4

bcc 0.5 FeBe B32 −9.3

bcc 0.75 FeBe

−18.6

bcc 1 Be A2 0.0

where φ denotes the type of superstructure and V is the

volume.

Then, the effective cluster interaction energies,

{ν

(V)}, can be extracted from these formation energies

using the cluster expansion method (CEM) developed

by Connolly and Williams [20.10]. This leads to a set of

composition-independent parameters, from which the

energy of the set of superstructures can be reproduced

in terms of a set of correlation functions {ξ

ΔE

form

(V) =



i=0

(V )×ξ

, (20.26)

where ν

(V ) is the effective interaction energy of the

i-point cluster, and ξ

is the correlation function for

cluster i in the phase φ; ξ

is deﬁned as the ensemble

average of the spin operator σ(p), which takes values

of ±1, depending on the atom occupancy of the lat-

tice site p. The values of ξ

for the superstructures

considered in this study are summarized in Table 20.3.

The formation energies to the segregation limit for the

−

Be binary system in the D0

, B2, B32, and A2

structures in the ground state are summarized in Ta-

ble 20.4 [20.11].

The upper limit of the summation in (20.26) γ speci-

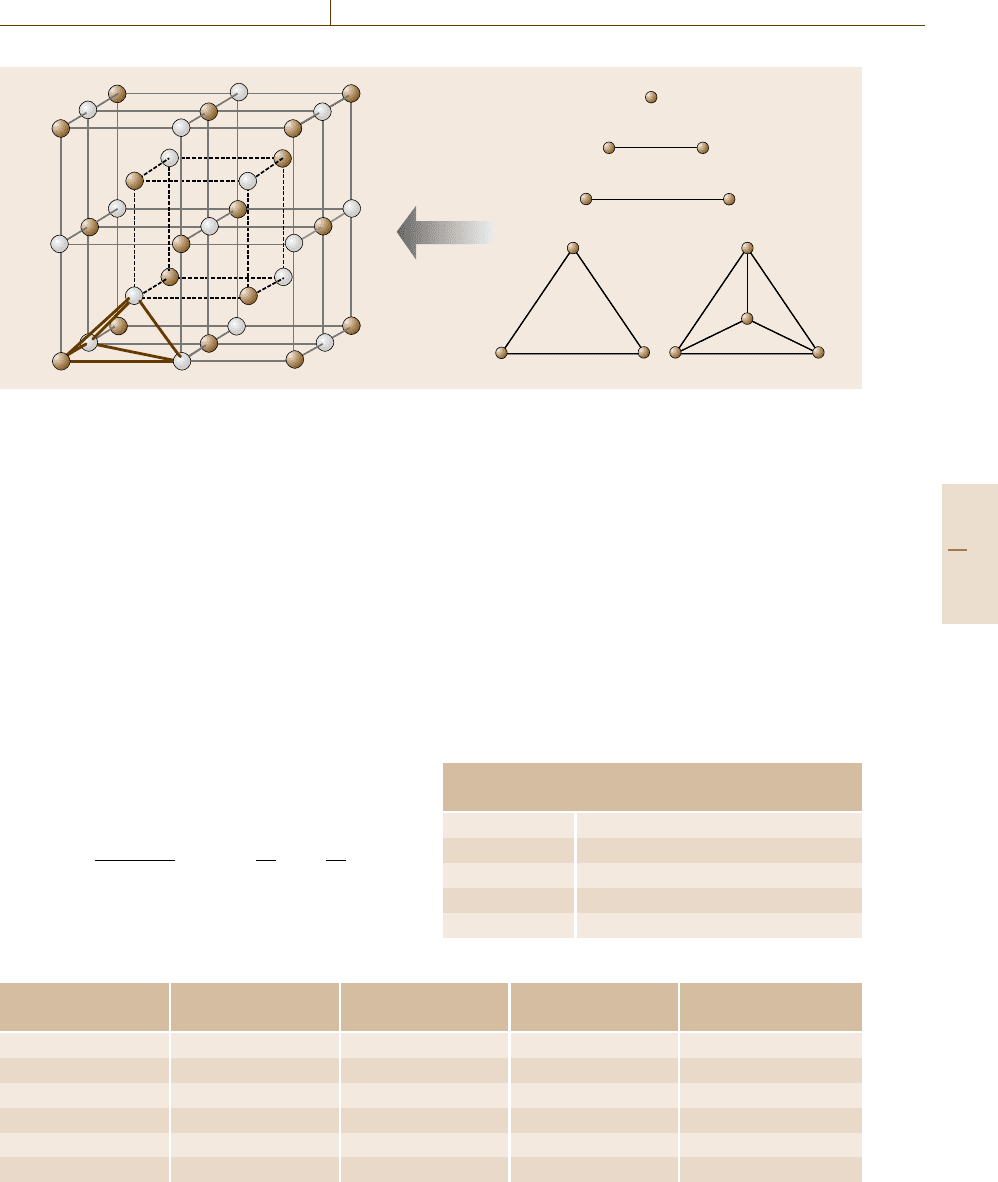
ﬁes the largest cluster that participated in the expansion.

In the case of the Fe

−

Be system, a tetrahedron cluster is

considered, as schematically illustrated in Fig. 20.4,as

being the largest cluster, since in the bcc structure, the

tetrahedron forms an irregular shape containing both the

Part E 20.2

The CALPHAD Method 20.2 Incorporation of the First-principles Calculations into the CALPHAD Approach 1069

Fig. 20.4 Various clusters consisting of ordered structures

ﬁrst- and second-nearest neighbor distances. The sec-

ond pair interaction was also taken into account, which

leads to the consequence that mathematically, ﬁve γ

should represent six types of cluster. From Table 20.3,

we can see that {ξ

} is a 6× 6 matrix and that it is a reg-

ular matrix. The matrix inversion of (20.26) yields the

effective interaction energies as

(V) =



i=0





−1

ΔE

form

(V) . (20.27)

Thus the interatomic interactions can be estimated by

expanding the total energies of the ordered structures

obtained from the band-energy calculations.

Using the Murnaghan equation of states [20.12], as

shownin(20.28), the total energies of the A2, B2, B32,

and the D0

structures were expressed as a function of

the volume

E(V ) =



−1)







1 −









−1







, (20.28)

Table 20.5 The coefﬁcient of the Murnaghan equation of states for the bcc superstructures

Structures B B



E(V

) V

(GPa) (Ry/a.u.

) (Ry) (a.u.

)

Fe (bcc) 334.2450 5.5525 −5091.1796 155.5298

Be (D0

) 75.3890 0.7851 −3833.1698 144.3524

FeBe (B2) 180.8774 3.6243 −2575.1689 124.0438

FeBe (B32) 87.6360 5.9438 −2575.1367 122.6823

FeBe

(D0

) 81.5496 3.6914 −1317.1225 112.6662

Be (bcc) 244.0350 3.0866 −59.0657 105.6658

where B, B



,andV

are the bulk modulus, its pressure

derivative, and the equilibrium volume, respectively,

at normal pressures. Table 20.5 shows the coefﬁcients

in (20.28) for each ordered structure. In this table,

E(V ) is the total energy of each ordered structure

in the equilibrium volume of the B2 structure; i. e.,

= 124.0438 a.u.

. The formation energy of each

structure is represented as ΔE

form

, by deﬁning the

average concentration of the total energy of the bcc

Fe and the bcc Be phases at the segregation limit.

By applying (20.28) to these formation energies, the

Table 20.6 The effective interaction {ν

(V )} correspond-

ing to the clusters

Effective cluster interactions (kJ/mol)

Tetrahedron CVM

−4.0

28.8

−4.8

4.0

6.2

Part E 20.2

1070 Part E Modeling and Simulation Methods

effective interaction, {v

(V )}, corresponding to each

cluster is calculated, as shown in Table 20.6, where

the positive numbers deﬁne the attractive force work-

ing between unlike atoms. The value of ν

represents

the interaction energy between the nearest neighbor

atoms, while ν

denotes the next-nearest neighbor

interaction.

The Gibbs free energies of the metastable bcc-based

phase in the Fe

−

Be binary system are evaluated us-

ing the effective cluster interaction energies up to the

tetrahedron cluster, including a second pair interaction

ΔE =



i=0

. (20.29)

At a ﬁnite temperature T the free energy of a phase

of interest ΔG can be obtained by adding a conﬁg-

urational entropy term ΔS to the internal energy as

follows [20.13,14]:

ΔG = ΔE −TΔS . (20.30)

The cluster variation method (CVM) with the tetrahe-

dron approximation are used to calculate the conﬁg-

urational entropy. For the bcc structure, the entropy

–5

–10

–15

–20

–25

–30

–35

0.2 0.4 0.6 0.8Fe Be

–5

–10

–15

–20

–25

–30

–35

0.2 0.6 0.8Fe Be0.4

Gibbs free energy ΔG (kJ mol) Gibbs free energy ΔG (kJ mol)

227°C

ab initio calculation

727°C

bcc–A2

bcc–B2

bcc–A2

bcc–B2

Molar fraction x

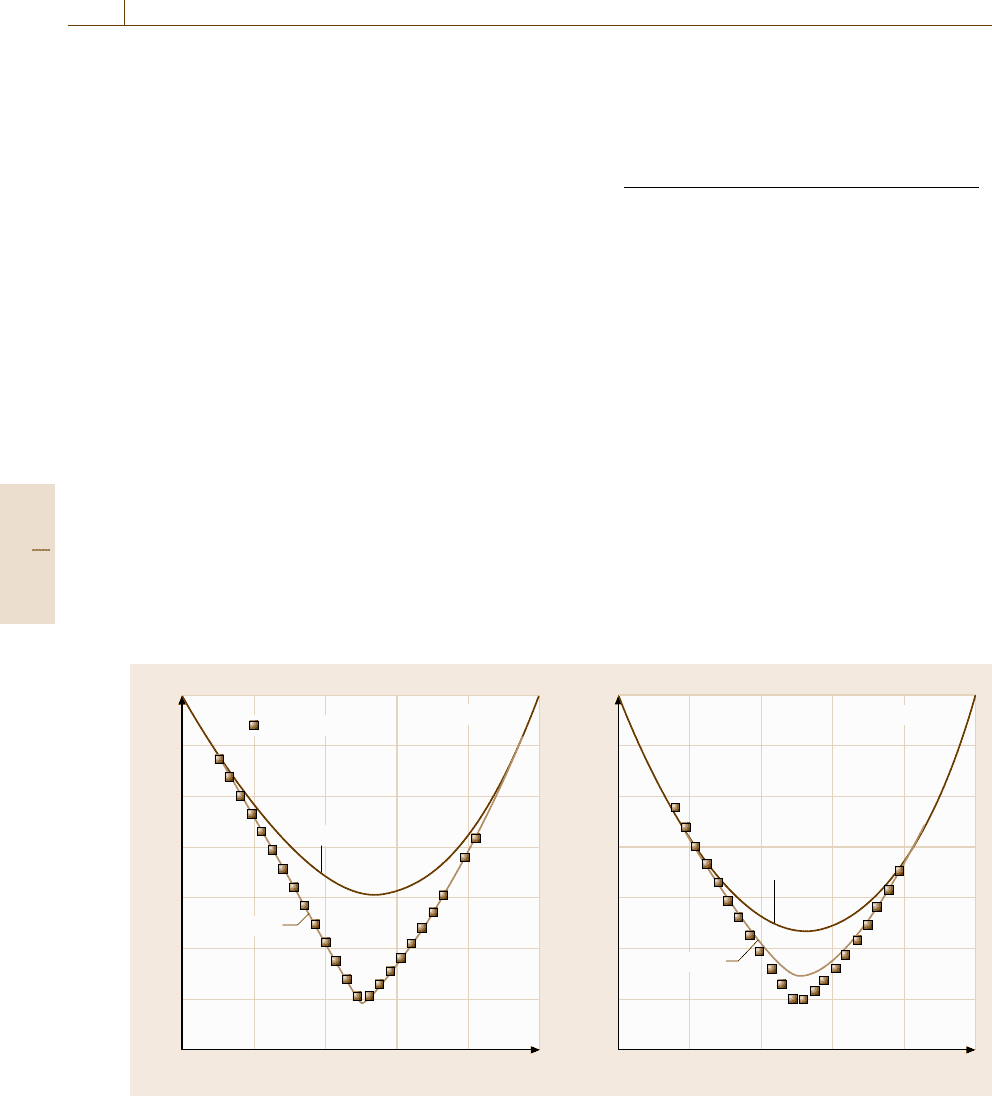
Fig. 20.5 The Gibbs energies of mixing in the α bcc solid solution at 227

◦

C and 727

◦

C based on ab initio energetic

calculations

formula is

ΔS = k





i, j,k



ijk









(

)







i, j,k,l



ijkl









i, j











i, j







(20.31)

where x

, y

, z

ijk

,andw

ijkl

are the cluster probabil-

ities of ﬁnding the atomic conﬁgurations speciﬁed by

the subscript(s) at a point, the nearest neighbour pair,

the second-nearest neighbour pair, the triangle, and the

tetrahedron clusters, respectively, and N is the number

of lattice points. Minimizing the grand potential with

respect to all the correlation functions allows for the

Gibbs energy of mixing to be obtained as a function of

composition at a constant temperature, T.

The compositional variation of the formation en-

thalpy derived by the cluster expansion and the cluster

variation methods is shown in Fig. 20.5 [20.11]. The

solid lines show the results of thermodynamic analyses

described in the following section. The open squares de-

note the corresponding Gibbs free energy derived by the

method shown in this section.

Part E 20.2

The CALPHAD Method 20.2 Incorporation of the First-principles Calculations into the CALPHAD Approach 1071

20.2.3 Thermodynamic Analysis

of the Gibbs Energies Based

on the First-principles Calculations

The Gibbs free energy of the bcc phase derived using

the ﬁrst-principles calculations is analyzed according to

the two-sublattice model. According to Table 20.4,the

most stable ordered structure in the Fe

−

Be bcc phase

is recognized as a B2 structure, and hence the Gibbs

free energy for this simple structure is described in this

section. The Gibbs energy for one mole of φ phase,

denoted as (Fe, Be)

(Fe, Be)

, is represented by the

two-sublattice model as described in Sect. 20.1.1 as the

following equation:

= y

Fe:Fe

Fe:Be

Be:Fe

Be:Be

+RT



m +n



ln y



m +n



ln y



mag

. (20.32)

The term y

denotes the site fraction of element i in

the sublattice s. The terms m and n are variables denot-

ing the size of the sublattice s, and straightforwardly,

the relationships of m = 0.5andn = 0.5 hold for the

B2 structure.

i:j

denotes the Gibbs energy of a hy-

pothetical compound i

0.5

, and terms relative to the

same stoichiometry are identical, whatever the occupa-

tion of the sublattice. The excess Gibbs energy term,

, contains the interaction energy between unlike

atoms, and is expressed using the following polynomial

= y

Fe,Be:Fe

Fe,Be:Be

Fe:Fe,Be

Be:Fe,Be

(20.33)

where L

i, j:k

(or L

i:j,k

) is the interaction parameter

between unlike atoms on the same sublattice. The mag-

netic contribution to the Gibbs free energy G

mag

was

given by (20.11).

The thermodynamic parameters obtained by ﬁtting

the ab initio values to (20.32) are shown as follows:

Be:Fe

−0.5

bcc

−0.5

bcc

=−37 100 +9T (J/mol) ,

Fe:Be

−0.5

bcc

−0.5

bcc

=−37 100 +9T (J/mol) ,

Be,Fe:Be

Be:Be,Fe

=−4T (J/mol) ,

Fe:Be,Fe

Be,Fe:Fe

=−380−4T (J/mol) .

The calculated Gibbs energies of mixing in the α bcc

solid solution at 227 and 727

◦

CaredrawninFig.20.5

using the solid lines for the ordered state (bcc−B2) and

the disordered state (bcc−A2), respectively. The con-

vex curvature of the free energy in the vicinity of the

equiatomic composition corresponds to the formation

of the B2 structure.

20.2.4 Construction of Stable

and Metastable Phase Diagrams

The information on the experimental data on the phase

boundaries and other thermodynamic quantities are

thermodynamically analyzed together with the esti-

mated metastable quantities of the bcc phase described

in the foregoing section.

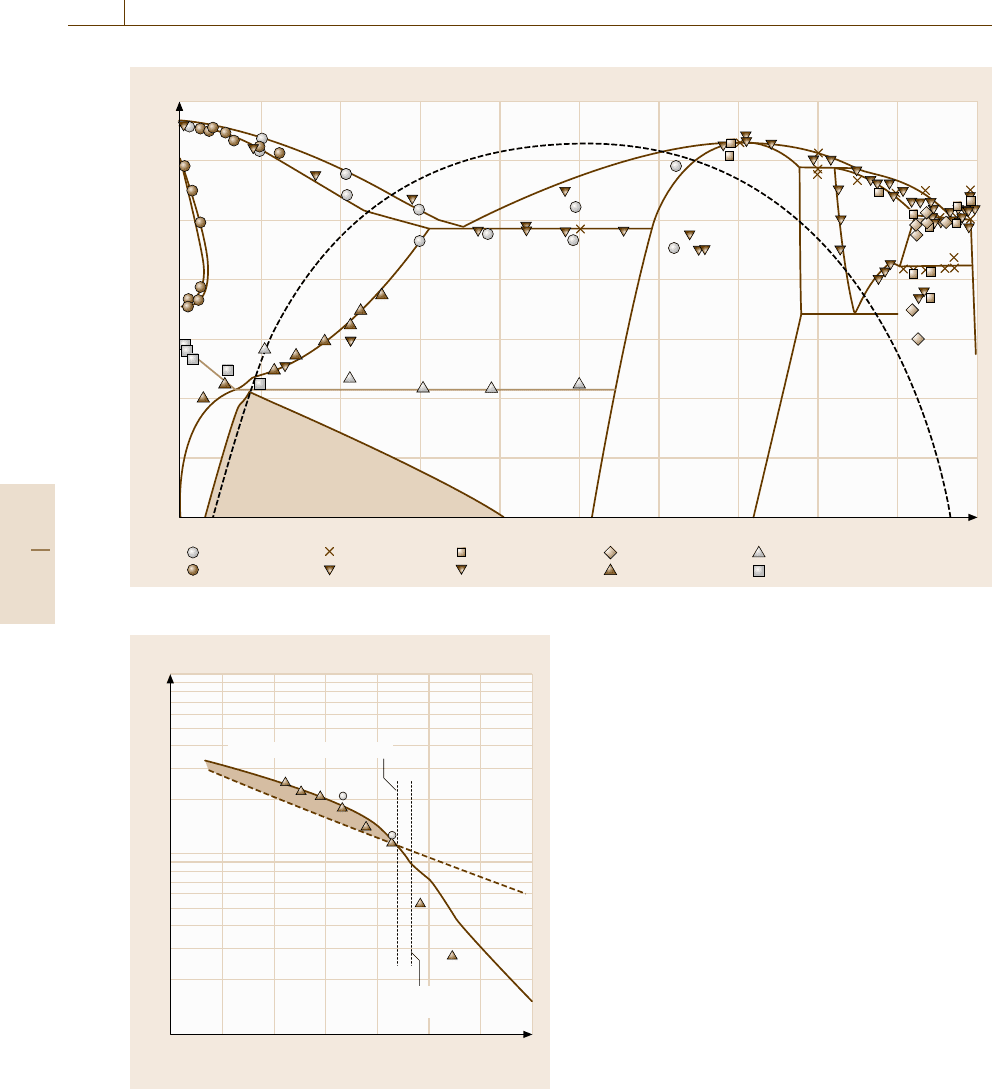
The calculated results of the Fe

−

Be phase diagram

are compared with the experimental data in Fig. 20.6.

The shaded area shown in this ﬁgure is the metastable

(bcc+B2) two-phase region, which is accompanied by

the ordering of the bcc structure on formation. The dot-

ted line shows the order–disorder transition line, along

which the two-phase ﬁeld expands into the higher tem-

perature range. The age hardening of this alloy has been

investigated experimentally and the results are summa-

rized in [20.15], and a brief outline of the ageing process

of this alloy is as follows. The disordered bcc structure

forms in the initial stage, and consequently, the B2-type

ordered structure separates in the bcc phase. A 100

modulated structure with changes in concentration was

observed in some samples using electron microscopy.

This ordering behavior of the bcc structure is possibly

explained by the metastable equilibria in Fig. 20.6.

It is well known that the solubility of Be in bcc

Fe (α) deviates signiﬁcantly from the Arrhenius equa-

tion; i. e., a proportional relationship exists between the

logarithm of the solubility and the reciprocal of the tem-

perature. The solubility of Be in the α phase is shown

in Fig. 20.7. The solubility would be denoted by the

broken line if there were neither an order–disorder tran-

sition nor a magnetic transition in the bcc Fe phase.

This is approximated by the straight line following the

Arrhenius law for dilute solutions. Thus, the deviation

of the solubility from the ideal Arrhenius law is repre-

Part E 20.2

1072 Part E Modeling and Simulation Methods

1600

1400

1200

1000

800

600

400

200

Fe 10 20 30 40 50 60 70 80 90 Be

Be (mol. %)

Temperature T (°C)

Oesterheld

Wever

Geles

Heubner

Hammond

Oesterheld

Wever

Gordon

Teitel

bcc + B2

Fig. 20.6 Calculated Fe

−

Be phase compared with experimental data

6 7 8 9 10 11 12 13

Reciprocal temperature 10

/T (K

–1

)

Order–disorder transition

Magnetic

transition

Solubility of Be in α-Fe (mol. %)

Fig. 20.7 Solubility of Be in the α phase

sented by the shaded areas. The dashed lines show the

order–disorder transition temperature and the magnetic

transition temperature of the bcc Fe phase. The solu-

bility of Be decreases in the lower temperature region

below 650

◦

C, while it increases in the higher temper-

ature region. The decrease in solubility in the lower

temperature region can be explained from the viewpoint

of the change in magnetism [20.16]. On the other hand,

the solubility increases owing to the order–disorder

transition of the bcc phase in the higher temperature

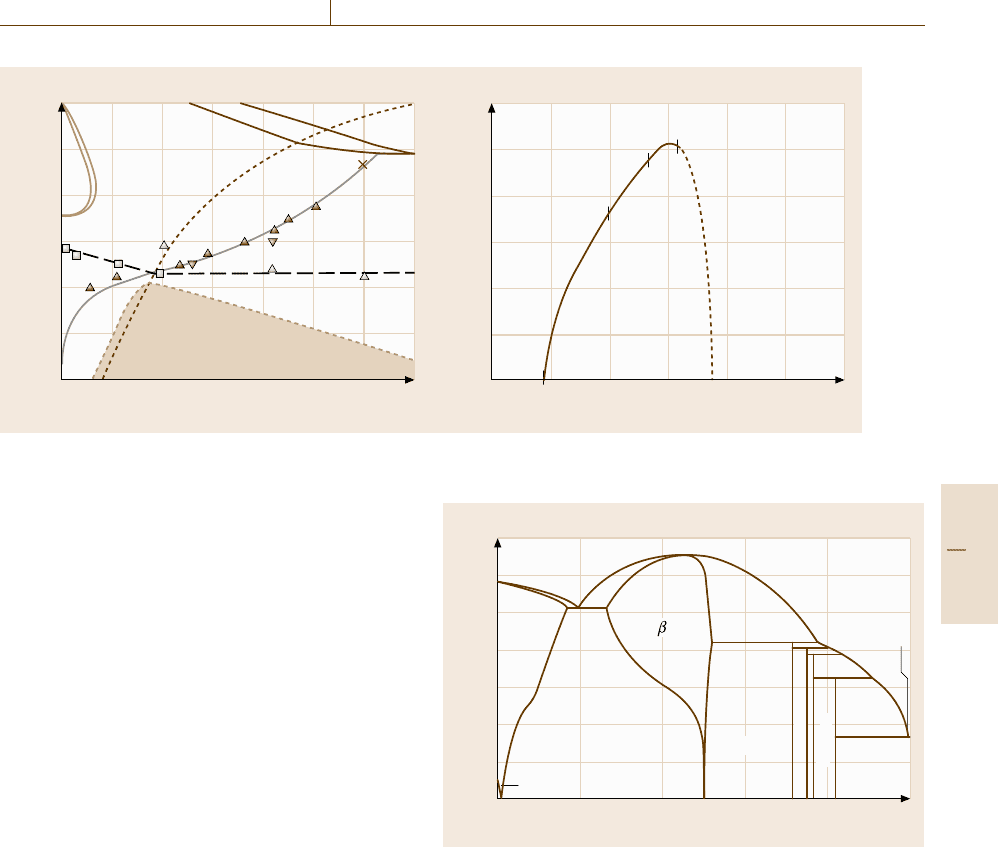
range. Figure 20.8 shows the change in the order pa-

rameter along a solubility line for the α phase. The order

parameter was deﬁned by

η = y

−y

. (20.34)

The solubility line in Fig. 20.8a intersects the order–

disorder transition line indicated by the dotted line at

about 650

◦

C. As can be seen in Fig. 20.8b, the order

parameter along the solubility line increases at a higher

temperature than 650

◦

C, yielding the progress of the

B2 ordering in the bcc disordered phase.

Part E 20.2

The CALPHAD Method 20.2 Incorporation of the First-principles Calculations into the CALPHAD Approach 1073

1400

1200

1000

800

600

400

200

Fe 5 101520253035

Be (mol. %)

0.6

0.5

0.4

0.3

0.2

0.1

Be contenet in α phase (mol. %)

Fe 10 20 30 40 50 60

a) Temperature T (°C)

bcc+B2

b) Order parameter

1190 °C

1000 °C

830 °C

650 °C

Fig. 20.8 (a) Enlarged Fe-rich portion of the calculated Fe

−

Be binary phase diagram. The dotted line shows the order–

disorder transition line. (b) Change in the order parameter along the solubility line for the α phase

20.2.5 Application to More Complex Cases

In the foregoing Sect. 20.2.3, two-sublattice formalism

was applied to describe the Gibbs energies derived

from the ﬁrst-principles calculations. However, it is

generally true that a more complex thermodynamic for-

malism such as a four-sublattice model is appropriate

so as to reﬂect directly the results of the ab initio

values in phase diagram computations, since several

stoichiometric compositions are selected for superstruc-

tures, i. e., A

B–D0

, AB-B2, AB-B32, AB

–D0

etc.

in the bcc phase. Then in this section, an analysis of

metastable phase separation of bcc phase in the Co

−

and Ni

−

Al binary systems is presented [20.17] using

the four-sublattice model. The more complex thermo-

dynamic modeling brings a detailed knowledge about

the metastable phase equilibria in these binary systems.

The Co

−

Al phase diagram consists of liquid, two

fcc solid solutions γ (Co) and γ (Al), hcp Co(ε), β with

CsCl structure, and the intermetallic phases Co

CoAl

,Co

,andCo

, as shown in Fig. 20.9.

There exists one eutectic reaction concerning the li-

quid phase and six invariant reactions between the solid

phases. The B2 (β) phase has a large homogeneity

range at higher temperatures, but the range decreases

remarkably in the lower temperature region. It has been

conﬁrmed experimentally that the two-phase region for

the A1(γ )/B2(β) phases extends over a wide com-

position range with decreasing temperature. Owing to

a sudden drop in the homogeneous region, these exper-

imental values were debatable.

2000

1800

1600

1400

1200

1000

800

600

Co 20 40 60 80 Al

Temperature T(K)

Al (mol.%)

γ(Co)

(hcp)

γ (Al)

CoAl

Fig. 20.9 Outline of the Co

−

Al binary phase diagram

Formation Energies of Superstructures

for the Co–Al System

The formation energies to the segregation limit for

the Co

−

Al system in the D0

, B2, B32 structures in

the ground state are summarized in Table 20.7, where

the corresponding values for the Ni

−

Al system are

included. The Gibbs free energies of the metastable bcc-

based phase are evaluated using the effective cluster

interaction energies up to the tetrahedron cluster, in-

cluding the second pair interactions. Using the same

procedure as in Sect. 20.2.2, the Gibbs energy of mix-

ing can be obtained as a function of composition at

a constant temperature T .

Part E 20.2

1074 Part E Modeling and Simulation Methods

Table 20.7 Formation energies to the segregation limit for Co

−

Al and Ni

−

Al in the D0

, B2, B32, and A2 structures in

the ground state

Alloy system Molar fraction of Al Structure Formation energy (kJ/mol)

−

Al 0.25 D0

−12.7

0.5 B2 −62.3

0.5 B32 −23.7

0.75 D0

−18.3

−

Al 0.25 D0

−40.7

0.5 B2 −69.5

0.5 B32 −34.0

0.75 D0

−18.2

Expression of Gibbs Energy of the B2 Phase

Using the Four-Sublattice Model

The β phase was described using a four-sublattice

model, so as to reﬂect the results of the ab initio cal-

culations on the phase diagram computation as





0.25





0.25





0.25





0.25

. (20.35)

The number of each sublattice site is 0.25, and the four

sites are therefore equivalent. The disordered state is de-

scribed when the site fractions of the different species

are the same in the four sublattices. For the ordered

structures, if two sublattices have the same site frac-

tions, as do the two others, but are different, then the

–10

–20

–30

–40

–50

–60

–70

Co Al0.2 0.4 0.6 0.8

Gibbs free energy ΔG (kJ/mol)

Molar fraction x

ab initio calculation

Thermodynamic analysis

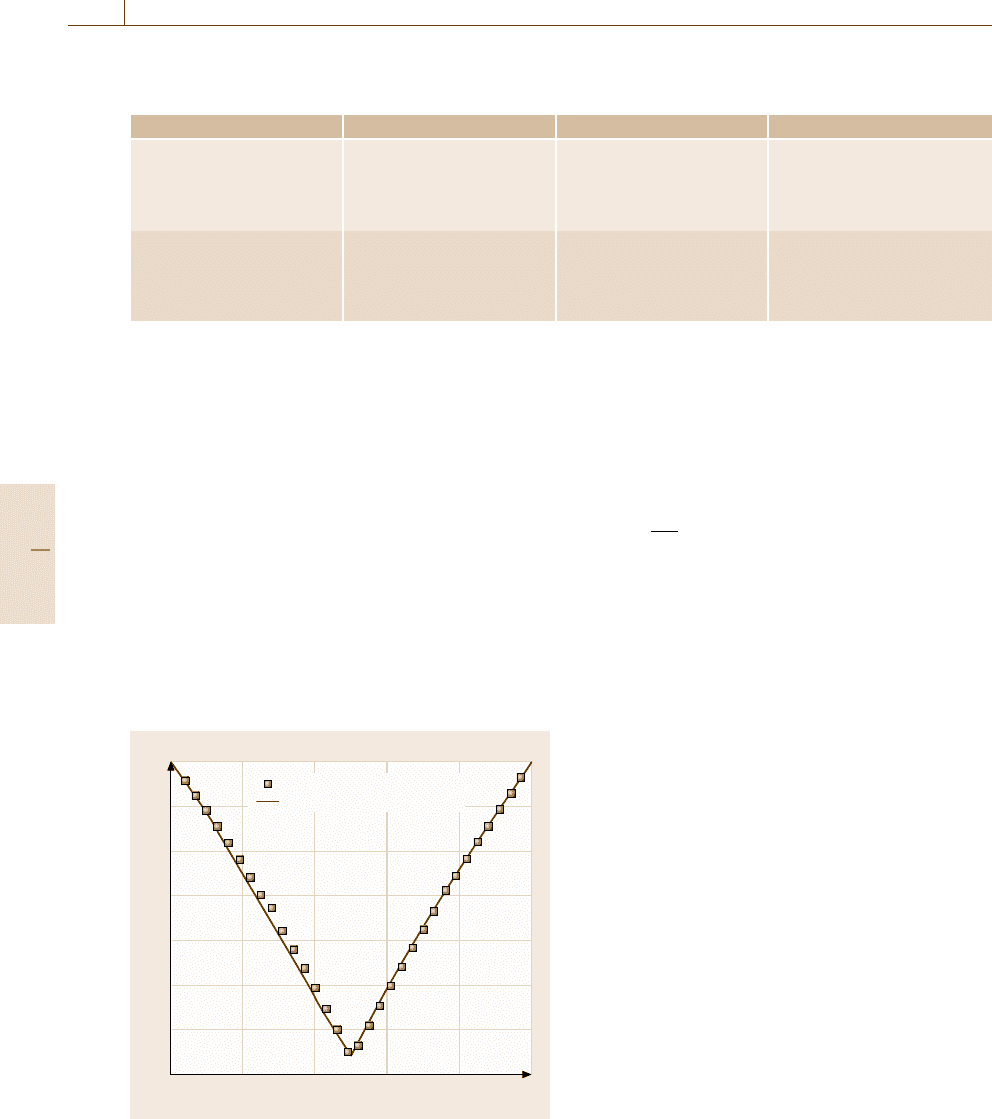
Fig. 20.10 The calculated Gibbs free energy of the bcc

phase in the Co

−

Al binary system at 727

◦

C compared

with the results from the ab initio energetic calculations

model describes the B2 and B32 phases. If three sublat-

tices have the same site fractions, and are different from

the fourth, then D0

ordering is described.

The Gibbs energy of the β phase is expressed by



i:j:k:l



s=1









s=1



j>i



i, j:k:l:m

(20.36)

where

i:j:k:l

denotes the Gibbs energy of a compound

0.25

, and terms relative to the same stoi-

chiometry are identical, whatever the occupation of the

sublattice. L

i, j:k:l:m

is the interaction parameter between

unlike atoms on the same sublattice.

Calculated Phase Equilibria

in the Co–Al Binary System

The calculated Gibbs free energy of the bcc phases

at 727

◦

C was compared with the results from the ab

initio energetic calculations in Fig. 20.10. The calcu-

lated Co

−

Al binary phase diagram is compared with

the experimental data in Fig. 20.11. The characteristic

features of the binary phase diagram are well repro-

duced by the calculations. The dotted line shows the

metastable two-phase separated region between the A2

(bcc-Co) and the B2 (β) phases. The two-phase sepa-

ration, based on the bcc structure, closely relates the

anomaly in the phase boundaries in the Co

−

Al bi-

nary system. This situation is schematically illustrated

in Fig. 20.12, where the Gibbs free energies of the B2

(β)andtheA1(γ (Co)) phases are drawn. The two-

phase separation of the β phase does not occur at higher

temperatures T

mainly owing to the effect of the en-

Part E 20.2

The CALPHAD Method 20.2 Incorporation of the First-principles Calculations into the CALPHAD Approach 1075

2000

1800

1600

1400

1200

1000

800

600

400

40 60 80 AlCo 20

Temperature T(K)

Al (mol. %)

γ(Co)

γ(Al)

CoAl

Gwyer

Fink

Koester

Schramm

Ettenberg

Takayama

Fig. 20.11 A comparison of the calculated Co

−

Al binary phase diagram with previous work

2000

1800

1600

1400

1200

1000

800

600

400

20 40 60 80Co Al

Al (mol. %)

Temperature T(K)Gibbs free energy

Al (mol. %)

T = T

Gibbs free energy

Al (mol. %)

T = T

γ(Co)

T = T

Fig. 20.12 The schematic Gibbs free energies of the B2 (β)andA2(γ (Co)) phases in the Co

−

Al system

Part E 20.2

1076 Part E Modeling and Simulation Methods

tropy of random mixing on the atomic arrangement.

On the other hand, the tendency towards ordering be-

comes stronger at lower temperatures T

.IntheB2

structure, the interaction between unlike atoms strength-

–10

–20

–30

–40

–50

–60

–70

Ni 0.2 0.4 0.6 0.8 Al

Gibbs free energy ΔG (kJ mol)

ab initio calculation

Thermodynamic analysis

Molar fraction x

Fig. 20.13 Calculated Gibbs free energy of the bcc phase

in the Ni

−

Al binary system at 727

◦

C compared with the

results from the ab initio energetic calculations

2000

1800

1600

1400

1200

1000

800

600

400

Ni 20 40 60 80 Al

Temperature T(K)

γ(Ni)

Al (mol. %)

γ(Al)

NiAl

Fink

Alexander

Phillips

Taylor

Nash

Robertson

Hilpert

Verhoeven

Jia

Fig. 20.14 A comparison of the calculated Ni

−

Al binary phase diagram with previous work

ens around the 50% Al composition, since the degree

of order reaches a maximum at the equiatomic com-

position. The decrease in the enthalpy term due to the

attractive interaction results in the acute point in the

free energy curve in the vicinity of the 50% Al compos-

ition, and consequently, a two-phase separation in the

β phase forms. This situation yields a signiﬁcant shift of

the phase boundary for the (γ (Co)+β)/β composition

to the equiatomic composition.

The procedure used for the Co

−

Al binary system

is applied to the Ni

−

Al binary system. The calculated

Gibbs free energy of the bcc phase is compared with

the results of the ab initio energetic calculations in

Fig. 20.13. The calculated Ni

−

Al binary phase diagram

is compared with the experimental data in Fig. 20.14.

The phase separation of the A2 and B2 structures can

not be observed in this binary system.

Origin of Phase Separation in the Co–Al

and Ni–Al Systems

The formation energies to the segregation limit for

−

Al and Ni

−

Al in the D0

, B2, B32, and A2 struc-

tures in the ground state, as listed in Table 20.7, are

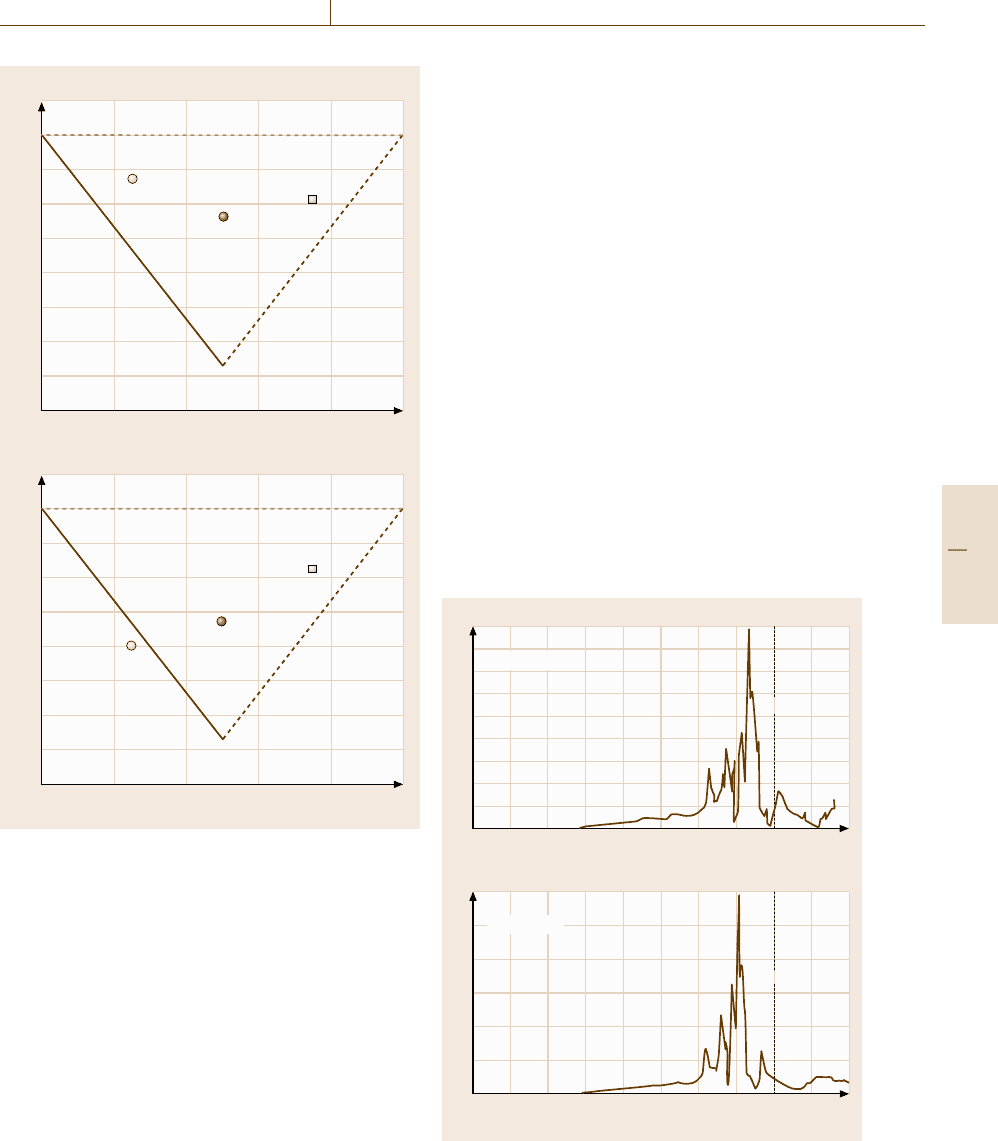
plotted versus Al concentration in Fig. 20.15.Incom-

paring the two systems, it can be seen that in the Co

−

system, the energy of the D0

structure at the 25% Al

Part E 20.2

The CALPHAD Method 20.2 Incorporation of the First-principles Calculations into the CALPHAD Approach 1077

–10

–20

–30

–40

–50

–60

–70

–80

Co 0.2 0.4 0.6 0.8 Al

–10

–20

–30

–40

–50

–60

–70

–80

Ni 0.2 0.4 0.6 0.8 Al

Formation energy ΔE (kJ mol)

Molar fraction x

bcc-Co bcc-Al

CoAl-B2

Al-D03

CoAl-B32

CoAl

-D03

bcc-Ni bcc-Al

NiAl

-D03

NiAl-B32

Al-D03

Fig. 20.15 Variation of the formation energies to the seg-

regation limit for Co

−

Al and Ni

−

Al with concentration

of Al

composition is located slightly above the straight line

connecting the energy values at the 0% Al and 50% Al

compositions, which results in a two-phase separation

of the A2 (bcc-Co) and B2 (β) structures in Co

−

that is more stable than the formation of the Co

Al–D0

structure in the ground state. On the other hand, the en-

ergy plot of the Ni

−

Al system shows the stabilization of

the Ni

Al–D0

structure compared with the two-phase

separation of the A2 (bcc-Ni) and B2 (β) structures,

since the formation energy of the D0

phase is lower

than the straight line connecting the energy values at the

0% Al and 50% Al compositions. This energetic analy-

sis suggests that a two-phase separation of the bcc-Co

andB2(β) phases occurs on the Co rich side in Co

−

system, while such a separation is not realized in the

−

Al system.

Figure 20.16 shows the density of states (DOS)of

the B2 (β) structure in the Co

−

Al and Ni

−

Al alloy

systems. In this ﬁgure, E

denotes the Fermi energy,

where no electrons occupy the electronic states above

this energy level. It can be seen that the distribution of

the DOS of the B2 phase in the two systems is simi-

lar, with both showing a low DOS at the Fermi level.

However, when observing the DOS of the D0

phase

for these two systems, as shown in Fig. 20.17, we ob-

serve a marked difference between these two systems,

in that the Fermi level is located near the peak of the

DOS for the Co

Al–D0

phase but decreases in a region

with a very low DOS in the Ni

Al–D0

phase. This fact

indicates that from an energetic point of view, the sta-

ble D0

structure of the Ni

Al phase is highly preferred,

while in the Co

Al–D0

phase is unstable with respect

to separation of the A2 and B2 phases in the Co

−

system.

–16 –14 –12 –10 –8 –6 –4 –2 0 2 4

Total density of states

Energy E (eV)

CoAl (B2)

NiAl (B2)

Fig. 20.16 The density of states of the B2 (β) structure in

the Co

−

Al and Ni

−

Al alloy systems

Part E 20.2