Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing
Подождите немного. Документ загружается.

1048 Part E Modeling and Simulation Methods
Depending on the value of B
2
−4AC in (19.80), it can
be categorized into elliptic, parabolic, and hyperbolic
typesasin(19.81), which are linked with steady heat
conduction problems, potential flow problems, steady
perfect elastic deformation problems, and so on
elliptic type B
2
−4AC < 0 ,
parabolic type B
2
−4AC =0 ,
hyperbolic type B
2
−4AC > 0 . (19.81)
In the following part, we study the characteristic of three
types.
19.5.1 Elliptic Type
If an independent variable t is replaced by y under the
conditions of A =C =1, B = D = E = F =0andG =
f (x, y)in(19.80), we get a so-called Poisson equation
∂
2
φ
∂x
2
+
∂
2
φ
∂y
2
= f (x, y) . (19.82)
The Laplace equation is in the case of f (x, y) =0
∂
2
φ
∂x
2
+
∂
2
φ
∂y
2
=0 . (19.83)
This type represents the problem of finding the steady
distribution of the target value inside the domain
with some boundary conditions such as steady heat
conduction problems (see Sect. 19.4.1), potential flow
problems (under the assumption of zero rotation = no
viscosity) and steady perfect elastic deformation prob-
lems (see Sect. 19.4.2).
From images of these phenomena, the characteris-
tics of elliptic-type phenomena can be summarized as
1. The equation type is usually for steady problems.
2. The solution at some point tends to be the averaged
values of the surrounding points.
19.5.2 Parabolic Type
Typical parabolic-type phenomena are unsteady heat
conduction or unsteady diffusion problems. For exam-
ple, by setting A =−1, E =1, and B =C = D = E =
F =0, we obtain the following equation, where t, x,and
φ(x, t) are time, the x-coordinate in one-dimension, and
the physical variable dependent on x and t,suchas
density or temperature
∂φ
∂t
=
∂
2
φ
∂x
2
. (19.84)
Both unsteady heat conduction problems and unsteady
diffusion problems belong to this type.
Equation (19.85) represents both unsteady heat con-
duction problems and unsteady diffusion problems in
one-dimensional case, where k is the heat conduction
coefficient and a diffusive coefficient, respectively
∂u(x, t)
∂t
−k
∂
2
u(x, t)
∂x
2
=−f . (19.85)
With the information above, the characteristics of
parabolic-type phenomena can be summarized as
1. Nondirectional distribution of the solution in space
2. Rapid diffusion of the solution in time over the do-
main.
19.5.3 Hyperbolic Type
A typical hyperbolic type is the wave equation below,
which is the case with A =−c
2
, C =1, and B = D =
E = F =0in(19.80). This equation represents the wave
propagation along the x direction with the velocity c,
which is called the wave equation
∂
2
φ
∂t
2
=c
2
∂
2
φ
∂x
2
. (19.86)
The second part of factorized equation below is called
an advection equation, which has almost equivalent
characteristics as a wave equation
∂
2
φ
∂t
2
−c
2
∂
2
φ
∂x
2
=
∂
∂t
−c
∂
∂x
∂
∂t
+c
∂
∂x
φ.
(19.87)
The characteristics of hyperbolic-type phenomena can
be summarized as
1. Directional distribution of the solution in space
2. Diffusion of the solution with given velocity in time
in some part of domain.
The advection–diffusion equation is given in (19.88),
where φ, u, k,and f are density, advective velocity,
diffusive coefficient, and source term, respectively
∂φ
∂t
+u
∂φ
∂x
−k
∂
2
φ
∂x
2
= f . (19.88)
As one can see from the previous explanation, hyper-
bolic and parabolic types show the opposite charac-
teristics. Since the advection–diffusion equation is the
combination of these two types, there exist some dif-
ficulties for numerical calculations. The flow problem,
described by Navier–Stokes equation, is a nonlinear
version of the advection–diffusion equation in a mathe-
matical sense.
Part E 19.5
Finite Element and Finite Difference Methods 19.6 Time Integration for Unsteady Problems 1049
19.6 Time Integration for Unsteady Problems
The governing equation of the unsteady heat conduction
problem in the one-dimensional case is represented as
follows, where u, k,and f are the temperature, the heat
conduction coefficient, and the heat source, respectively
∂u(x, t)
∂t
−k
∂
2
u(x, t)
∂x
2
=−f . (19.89)
Suppose that we know the values of u and ∂u/∂x at
time n, which is represented by u
n
and
˙
u
n
.Nowwewant
to obtain u
n+1
from u
n
and
˙
u
n
.
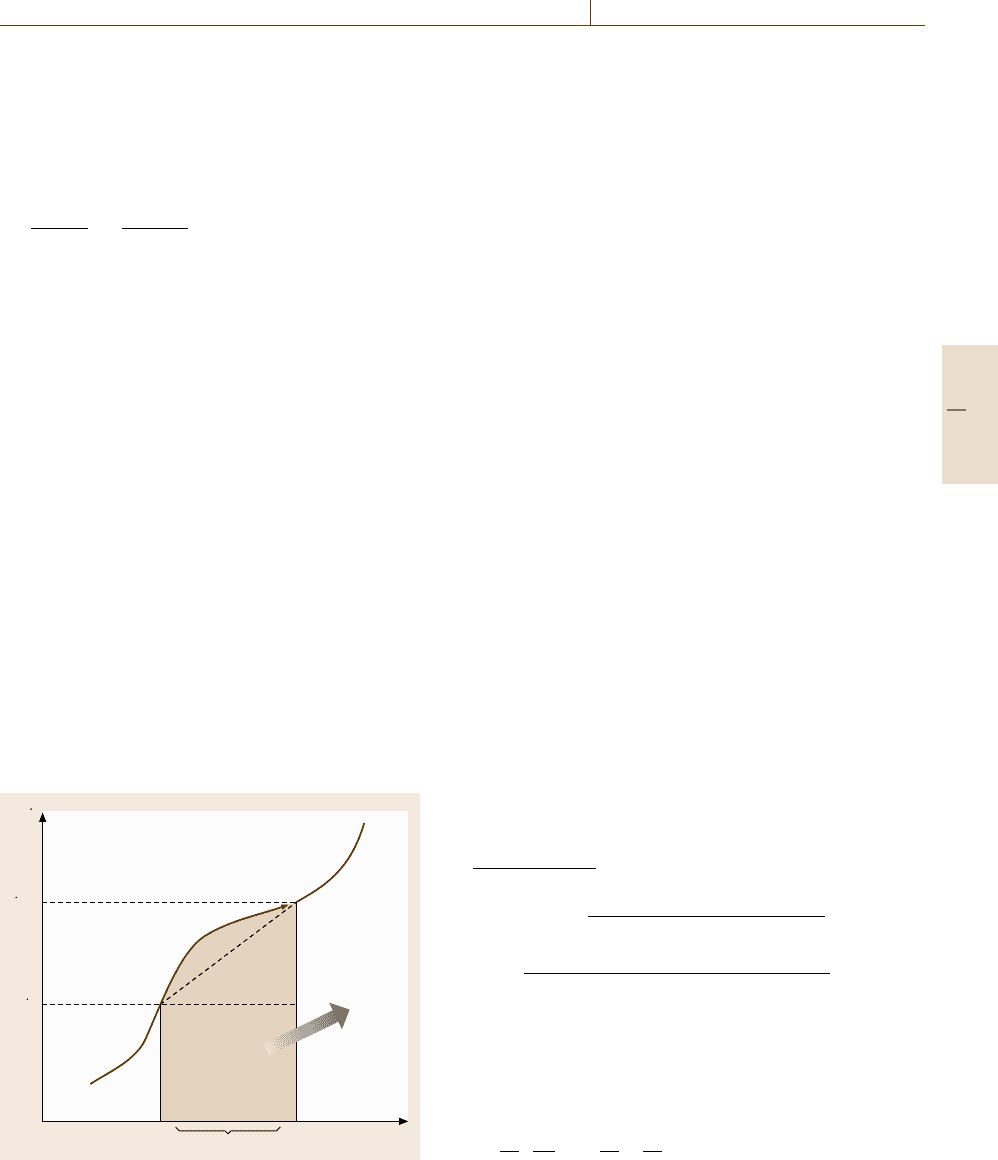
Figure 19.19 visualizes the problem. The shaded
part is u
n+1
−u
n
, which is what we want to obtain. The
finite difference idea is applied to this problem.
Let us simplify the problem by introducing the gen-
eralized trapezoidal method description [19.2], which is
nothing but a generalized finite difference description
using the parameter α
u
n+1
=u
n
+Δt
˙
u
n+α
,
˙
u
n+α
=(1 −α)
˙
u
n
+α
˙
u
n+1
. (19.90)
If α = 0, then u
n+α
=
˙
u
n
→u
n+1
=u
n
+Δt
˙
u
n
,which
means u
n+1
−u
n
is calculated by the known value
˙
u
n
at the nth time step as shown by the lower dotted line
in Fig. 19.19. This is a forward difference scheme wrt
time, which is called the forward Euler or the explicit
method.
If α =1, then
˙
u
n+α
=
˙
u
n+1
→u
n+1
=u
n
+Δt
˙
u
n+1
,
which means u
n+1
−u
n
is calculated by the unknown
value
˙
u
n+1
at (n +1)th time step. In Fig. 19.19, the up-
per dotted line illustrates this case. This is the backward
u
n+1
u
u
n
t
n+1
Area = u
n+1
–u
n
t
n
t
Δt
Fig. 19.19 Time integration between t
n
and t
n+1
difference method in time, named the backward Euler
or the implicit method.
If α = 0.5, then
˙
u
n+α
= (
˙
u
n
+
˙
u
n+1
/2) →u
n+1
=
u
n
+Δt(
˙
u
n
+
˙
u
n+1
/2), which means u
n+1
−u
n
is cal-
culated by both known and unknown values
˙
u
n
,
˙
u
n+1
at
the nth time step. In Fig. 19.19, this is the diagonal dot-
ted line. This is called the trapezoidal rule, the midpoint
rule, or the Crank–Nicolson method.
According to Fig. 19.19, the Crank–Nicolson meth-
od (α =0.5 case) seems to be the best solution, however
˙
u
n+1
is not known at the nth time step. Since
˙
u
n+1
is
also calculated with the Crank–Nicolson algorithm, it
is not a simple discussion. Based on experience, the
Crank–Nicolson method with α = 0.51 ≈ 0.55 is rec-
ommended in most cases.
Usually the unknown value
˙
u
n+1
is obtained by
a matrix inversion process in the implicit method
or Crank–Nicolson method in discretized numerical
schemes. In nonlinear cases, equilibrium iterations, for
example, the Newton–Raphson method (see Sect. 19.8)
within a time step is usually omitted in explicit time
integration.
In the following, the derivations of FDM and FEM
for the unsteady heat conduction problem in the one-
dimensional case is explained by the time integration
scheme explained above.
19.6.1 FDM
By applying the generalized finite difference descrip-
tion in time to a finite difference formulation at node
u
n
(x), we get
u
n+1
(x) −u
n
(x)
Δt
−k
(1 −α)
u
n
(x +h) −2u
n
(x) +u
n
(x −h)
h
2
+α
u
n+1
(x +h) −2u
n+1
(x)+u
n+1
(x −h)
h
2
(
=−f . (19.91)
After modifying the equation, it becomes
α
k
h
2
1
Δt
−2α
k
h
2
α
k
h
2
⎛
⎜
⎝
u
n+1
(x −h)
u
n+1
(x)
u
n+1
(x +h)
⎞
⎟
⎠
Part E 19.6
1050 Part E Modeling and Simulation Methods
+
(1−α)
k
h
2
−
1
Δt
−2(1−α)
k
h
2
(1 −α)
k
h
2
×
⎛
⎜
⎝
u
n
(x −h)
u
n
(x)
u
n
(x +h)
⎞
⎟
⎠
=−f . (19.92)
If α =0, the local FD equation becomes the following
one in matrix representation
0
1
Δt
0
⎛
⎜
⎝
u
n+1
(x −h)
u
n+1
(x)
u
n+1
(x +h)
⎞
⎟
⎠
+
k
h
2
−
1
Δt
−2
k
h
2
k
h
2
⎛
⎜
⎝
u
n
(x −h)
u
n
(x)
u
n
(x +h)
⎞
⎟
⎠
=−f .
(19.93)
After summing this equation for all nodes, we get the
following matrix system
1
Δt
Iu
n+1
+K
2
u
n
= F . (19.94)
Equation (19.94) means that a solution vector at
(n +1)th time step u
n+1
can be obtained merely by
u
n+1
= Δt(F −K
2
u
n
) without any matrix inversion.
This is an explicit case.
If α = 1, we get the following local matrix system
k
h
2
1
Δt
−2
k
h
2
k
h
2
⎛
⎜
⎝
u
n+1
(x −h)
u
n+1
(x)
u
n+1
(x +h)
⎞
⎟
⎠
+
0 −
1
Δt
k
h
2
0
⎛
⎜
⎝
u
n
(x −h)
u
n
(x)
u
n
(x +h)
⎞
⎟
⎠
=−f . (19.95)
After summing all equations,
K
1
u
n+1
−
1
Δt
k
h
2
Iu
n
= F . (19.96)
This matrix system denotes that a solution vector
at the (n +1)th time step u
n+1
is calculated by
u
n+1
= K
−1
1
(F +1/Δtk/h
2
Iu
n
) which involves the
matrix inversion K
−1
1
. This is an implicit case. The
Crank–Nicolson case with α =0.51–0.55 belongs to an
implicit case, since it needs matrix inversion calcula-
tion.
19.6.2 FEM
In FEM, the space domain is spanned by the finite el-
ement interpolation function, but the finite difference
idea in time is applied in the time domain.
Again, starting from the weak form, we get
1
0
∂u(x, t)
∂t
+k
∂
2
u(x, t)
∂x
2
+ f
w(x, t)dx = 0 ,
(19.97)
1
0
w
∂u(x, t)
∂t
dx +
1
0
k
∂w(x, t)
∂x
∂u(x, t)
∂x
dx
=
1
0
fw(x, t)dx −kw(0)b . (19.98)
By introducing the finite element functions as in
Sect. 19.1,
element j
w
1
(t) w
2
(t)
⎛
⎜
⎝
dN
1
(x)
dx
dN
2
(x)
dx
⎞
⎟
⎠
×
dN
1
(x)
dx
dN
2
(x)
dx
˙
u
1
(t)
˙
u
2
(t)
dx
+
element j
w
1
(t) w
2
(t)
⎛
⎜
⎝
dN
1
(x)
dx
dN
2
(x)
dx
⎞
⎟
⎠
×
dN
1
(x)
dx
dN
2
(x)
dx
u
1
(t)
u
2
(t)
dx
=
w
1
(t) w
2
(t)
element j
f
N
1
(x)
N
2
(x)
dx
−k
w
1
(t) w
2
(t)
N
1
(
0
)
N
2
(
0
)
b . (19.99)
Omitting weight function vector,
$
element j
⎛
⎜
⎝
dN
1
(x)
dx
dN
2
(x)
dx
⎞
⎟
⎠
×
dN
1
(x)
dx
dN
2
(x)
dx
dx
˙
u
1
(t)
˙
u
2
(t)
+
$
element j
k
⎛
⎜
⎝
dN
1
(x)
dx
dN
2
(x)
dx
⎞
⎟
⎠
×
dN
1
(x)
dx
dN
2
(x)
dx
dx
u
1
(t)
u
2
(t)
−
$
element j
f
N
1
(x)
N
2
(x)
dx −k
N
1
(0)
N
2
(0)
b =0 .
(19.100)
Part E 19.6
Finite Element and Finite Difference Methods 19.7 Multidimensional Case 1051
Now we get the following matrix representation,
where M and K are called the mass matrix and stiffness
matrix, respectively
M
˙
u(t)+Ku(t) = F(t)
where M =
$
element j
⎛
⎜
⎝
dN
1
(x)
dx
dN
2
(x)
dx
⎞
⎟
⎠
×
dN
1
(x)
dx
dN
2
(x)
dx
dx ,
K =
$
element j
k
⎛
⎜
⎝
dN
1
(x)
dx
dN
2
(x)
dx
⎞
⎟
⎠
×
dN
1
(x)
dx
dN
2
(x)
dx
dx ,
F =
$
element j
f
N
1
(x)
N
2
(x)
dx
−k
N
1
(0)
N
2
(0)
b . (19.101)
Combining the definition of the generalized trapezoidal
method as follows
M
˙
u
n+1
+Ku
n+1
= F
n+1
,
u
n+1
=u
n
+Δt
˙
u
n+α
,
˙
u
n+α
=(1−α)
˙
u
n+α
˙
u
n+1
, (19.102)
we finally get the following algorithm
1
αΔt
(
M +αΔtK
)
u
n+1
= F
n+1
+
1
αΔt
M
u
n
+(1 −α)Δt
˙
u
n
. (19.103)
It should be noted that both u
n
and
˙
u
n
should be
stored in the code for the Crank–Nicolson method.
In the case of α = 0, that is, the forward Euler case,
if the left-hand side mass matrix M is lumped (summing
the diagonal terms), u
n+1
can be obtained without seri-
ous matrix inversion. This is an explicit method, where
LS-DYNA and PAM-CRASH for crash FE analysis are
the most common pieces of software used for this type.
In the explicit time integration scheme (both in
FDM and FEM), the Courant–Friedrichs–Lewy (CFL)
condition is a key issue to determine a proper time step.
The CFL condition says that a time step must be less
than the time for some significant action to occur. In
other words, the Courant number defined in (19.104)
must be less than 1, where c, h,andΔt are dissipation
speed, mesh size, and time step. This means if one uses
a very fine mesh, one should also use a proper tiny time
step. The mesh size and the time step are linked together
in the explicit method by
ν =
c
h
Δt
=c
Δt
h
. (19.104)
19.7 Multidimensional Case
The multidimensional case is basically the extension of
one-dimensional case, but it is usually difficult to have
an image of derivations in matrix forms. Here we study
it without tensor description.
Let us consider the two-dimensional heat conduc-
tion problem, described by (19.105). In this case, we
consider isotropic heat conduction without any direc-
tional references (see (19.56) for a general description)
∂q
x
∂x
+
∂q
y
∂y
= f ,
with u =a on Γ
a
, −qn = b on Γ
b
,
where q =
q
x
q
y
=−
k 0
0 k
⎛
⎜
⎝
∂u(x, y)
∂x
∂u(x, y)
∂y
⎞
⎟
⎠
(Fourier’s law in the isotropic case) .
(19.105)
By substituting Fourier’s law to the partial differential
equation (19.105), we get
k
∂
2
u(x, y)
∂x
2
+
∂
2
u(x, y)
∂y
2
=−f . (19.106)
In the following part, we only consider (19.106) without
boundary conditions for simplicity.
19.7.1 Finite Difference Method
By extension of the one-dimensional definition in finite
difference operators, we can easily obtain the following
operators in the two-dimensional case
∂φ(x, y)
∂x
≈
φ(x +h, y) −φ(x −h, y)
2h
x
,
∂φ(x, y)
∂y
≈
φ(x, y +h) −φ(x, y −h)
2h
y
,
Part E 19.7
1052 Part E Modeling and Simulation Methods
∂
2
u(x, y)
∂x
2
≈
u(x +h, y) −2u(x, y) +u(x −h, y)
h
2
x
,
∂
2
u(x, y)
∂y
2
≈
u(x, y +h) −2u(x, y) +u(x, y −h)
h
2
y
.
(19.107)
Now let us consider two-dimensional finite difference
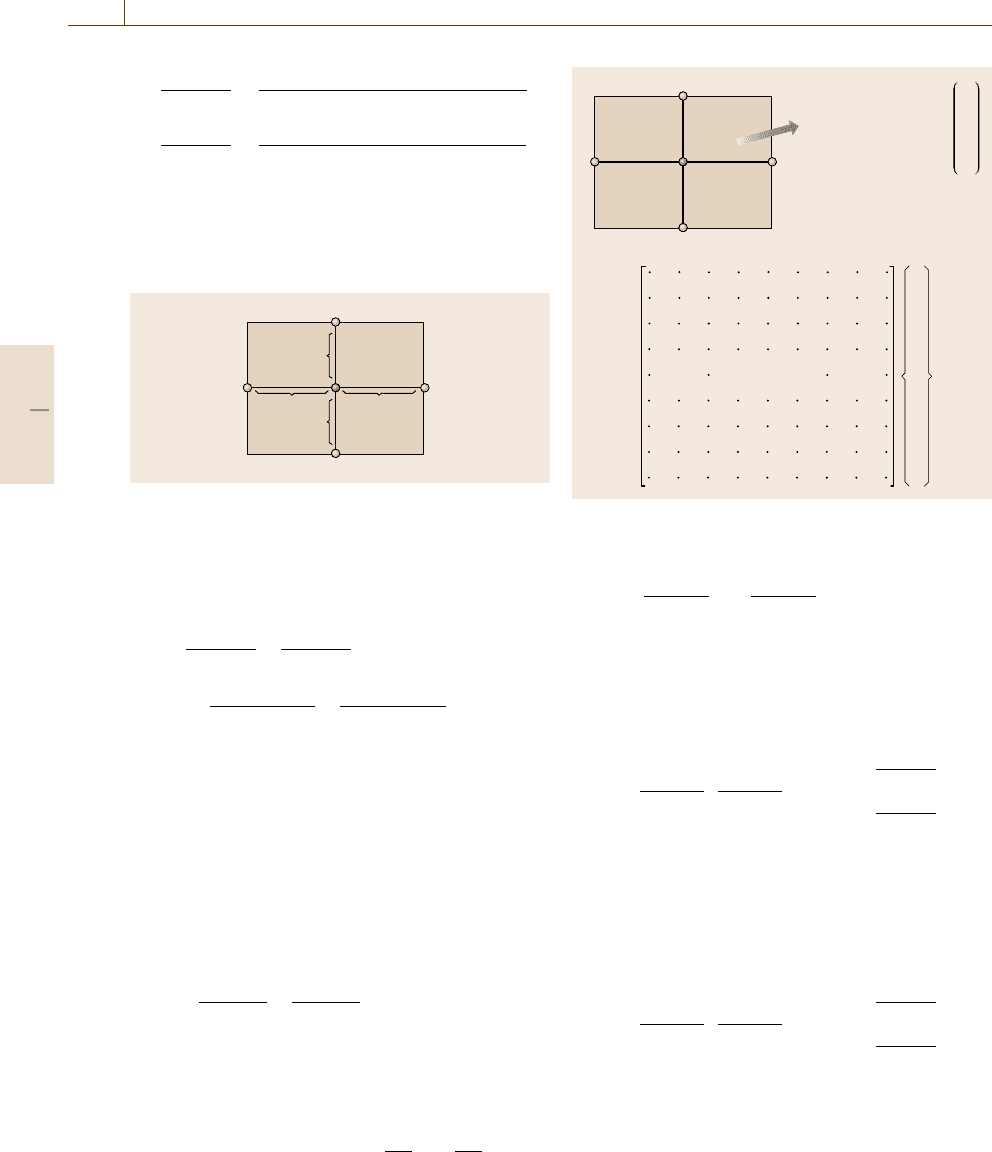
gridsinFig.19.20.
h
x
h
y
h
y
h
x
978
654
321
Fig. 19.20 Finite difference grids in the two-dimensional
case
Applying (19.107)to(19.106) at node 5 in
Fig. 19.19 gives
k
∂
2
u(x, y)
∂x
2
+
∂
2
u(x, y)
∂y
2
≈k
u
4
−2u
5
+u
6
h
2
x
+
u
2
−2u
5
+u
8
h
2
y
, (19.108)
which is visualized by the local and global matrix rep-
resentations in Fig. 19.21. The whole global matrix for
(19.106) is piled up without any overlap between rows.
19.7.2 Finite Element Method
As in Sect. 19.2, the weak form can be generated by
multiplying the weight function w with the governing
equationin(19.106). It should be noted that all func-
tions are assumed to be functions wrt x and y.
Ω
∂q
x
(x, y)
∂x
+
∂q
y
(x, y)
∂y
− f
w(x, y)dΩ =0
(19.109)
By applying integration by parts, or the Green–
Gauss theorem, we obtain
−
Ω
fw(x, y)dΩ +
Γ
b
w(x, y)
∂q
x
∂x
n
x
+
∂q
y
∂y
n
y
dΓ
987
654
321
(e
52
e
54
e
55
e
56
e
58
)
u
2
u
4
u
5
u
6
u
8
u
1
u
2
u
3
u
4
u
5
u
6
u
7
u
8
u
9
e
52
e
54
e
55
e
56
e
58
Fig. 19.21 Local (upper) and global matrix in two-
dimensional FDM
−
Ω
∂w(x, y)
∂x
q
x
+
∂w(x, y)
∂y
q
x
dΩ =0 .
(19.110)
After substituting Fourier’s law into (19.110), we
get the matrix form
Ω
∂w(x, y)
∂x
∂w(x, y)
∂y
k 0
0 k
⎛
⎜
⎝
∂u(x, y)
∂x
∂u(x, y)
∂y
⎞
⎟
⎠
dΩ
=
Ω
fw(x, y)dΩ +
Γ
b
w(x, y)bdΓ. (19.111)
Now we consider the left-hand term only, which is
Ω
j
∂w(x, y)
∂x
∂w(x, y)
∂y
k 0
0 k
⎛
⎜
⎝
∂u(x, y)
∂x
∂u(x, y)
∂y
⎞
⎟
⎠
dΩ.
(19.112)
As in Sect. 19.1, the variable (and its derivatives) are
represented by finite element shape functions, where
we consider the four-node bilinear quadrilateral finite
Part E 19.7
Finite Element and Finite Difference Methods 19.7 Multidimensional Case 1053
element
⎛
⎜
⎝
∂u(x, y)
∂x
∂u(x, y)
∂y
⎞
⎟
⎠
=
⎛
⎜
⎝
∂N
1
(x, y)
∂x
∂N
2
(x, y)
∂x
∂N
3
(x, y)
∂x
∂N
4
(x, y)
∂x
∂N
1
(x, y)
∂y
∂N
2
(x, y)
∂y
∂N
3
(x, y)
∂y
∂N
4
(x, y)
∂y
⎞
⎟
⎠
×
⎛
⎜
⎜
⎜
⎝
u
1
u
2
u
3
u
4
⎞
⎟
⎟
⎟
⎠
. (19.113)
Substituting (19.113)into(19.112)gives
Ω
j
w
1
w
2
w
3
w
4
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
∂N
1
∂x
∂N
1
∂y
∂N
2
∂x
∂N
2
∂y
∂N
3
∂x
∂N
3
∂y
∂N
4
∂x
∂N
4
∂y
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
k 0
0 k
×
⎛
⎜
⎝
∂N
1
∂x
∂N
2
∂x
∂N
3
∂x
∂N
4
∂x
∂N
1
∂y
∂N
2
∂y
∂N
3
∂y
∂N
4
∂y
⎞
⎟
⎠
⎛
⎜
⎜
⎜
⎝
u
1
u
2
u
3
u
4
⎞
⎟
⎟
⎟
⎠
dΩ. (19.114)
Omitting vectors w and u,
K
j
=
Ω
j
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
∂N
1
∂x
∂N
1
∂y
∂N
2
∂x
∂N
2
∂y
∂N
3
∂x
∂N
3
∂y
∂N
4
∂x
∂N
4
∂y
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
×
k 0
0 k
∂N
1
∂x
∂N
2
∂x
∂N
3
∂x
∂N
4
∂x
∂N
1
∂y
∂N
2
∂y
∂N
3
∂y
∂N
4
∂y
dΩ. (19.115)
Since FEM handles an arbitrary shaped domain, an ele-
ment’s shape is usually arbitrary. For this reason, finite
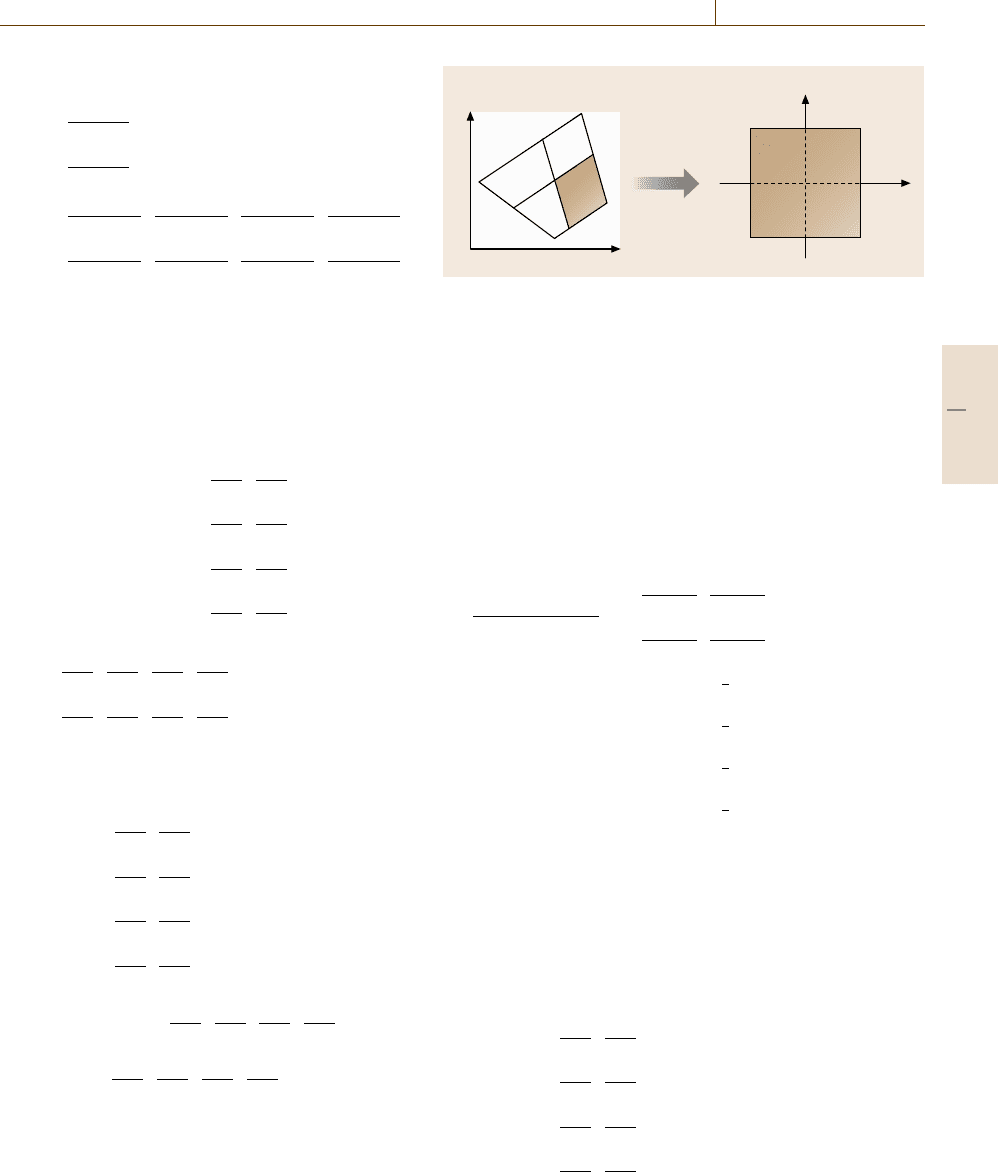
element functions in natural coordinates are used in the
y
a) b)
x
1
2
3
4
(–1,1) (1,1)
(–1,–1) (1,–1)
S
34
21
Fig. 19.22a,b Bilinear quadrilateral element: (a) Physical coordi-
nates, (b) natural coordinates
multidimensional case
u(x, y) =
4
$
k=1
u
k
N
k
(s, t) ,
x(s, t) =
4
$
k=1
x
k
N
k
(s, t) ,
y(s, t) =
4
$
k=1
y
k
N
k
(s, t) ,
∂
x(s, t), y(s, t)
∂(s, t)
=
⎛
⎜
⎝
∂x(s, t)
∂s
∂x(s, t)
∂t
∂y(s, t)
∂s
∂y(s, t)
∂t
⎞
⎟
⎠
,
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
N
1
(s, t) =
1
4
(1 −s)(1 −t) ,
N
2
(s, t) =
1
4
(1 +s)(1 −t) ,
N
3
(s, t) =
1
4
(1 +s)(1 +t) ,
N
4
(s, t) =
1
4
(1 −s)(1 +t) .
(19.116)
It should be noted that all finite element functions al-
ways have, in general, the following property
⎧
⎨
⎩
N
α
(s
β
, t
β
) =δ
αβ
,
)
n
α=1
N
α
(s, t) =1 .
(19.117)
Considering the Jacobian matrix between (x, y)and
(s, t),
K
j
=
Ω
j
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
∂N
1
∂s
∂N
1
∂t
∂N
2
∂s
∂N
2
∂t
∂N
3
∂s
∂N
3
∂t
∂N
4
∂s
∂N
4
∂t
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
k 0
0 k
Part E 19.7
1054 Part E Modeling and Simulation Methods
×
⎛
⎜
⎜
⎝
∂N
1
∂s
∂N
2
∂s
∂N
3
∂s
∂N
4
∂s
∂N
1
∂t
∂N
2
∂t
∂N
3
∂t
∂N
4
∂t
⎞
⎟
⎟
⎠
∂(x, y)
∂(s, t)
dΩ.
(19.118)
Local and global matrix representations around node 5
are visualized in Fig. 19.23.
Let us now show that the local stiffness matrix K
j
in the linear elastic solid case, which is treated in
Sect. 19.4, has the following form for the reader’s future
reference.
The relationship in (19.70)and(19.72) can be sum-
marized as shown in (19.119)
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
ε
xx
ε
yy
ε
zz
2ε
yz
2ε
zx
2ε
xy
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
∂
∂x
00
0
∂
∂y
0
00
∂
∂z
0
∂
∂z
∂
∂y
∂
∂z
0
∂
∂x
∂
∂y
∂
∂x
0
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
∂u
∂x
∂u
∂y
∂u
∂z
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
. (19.119)
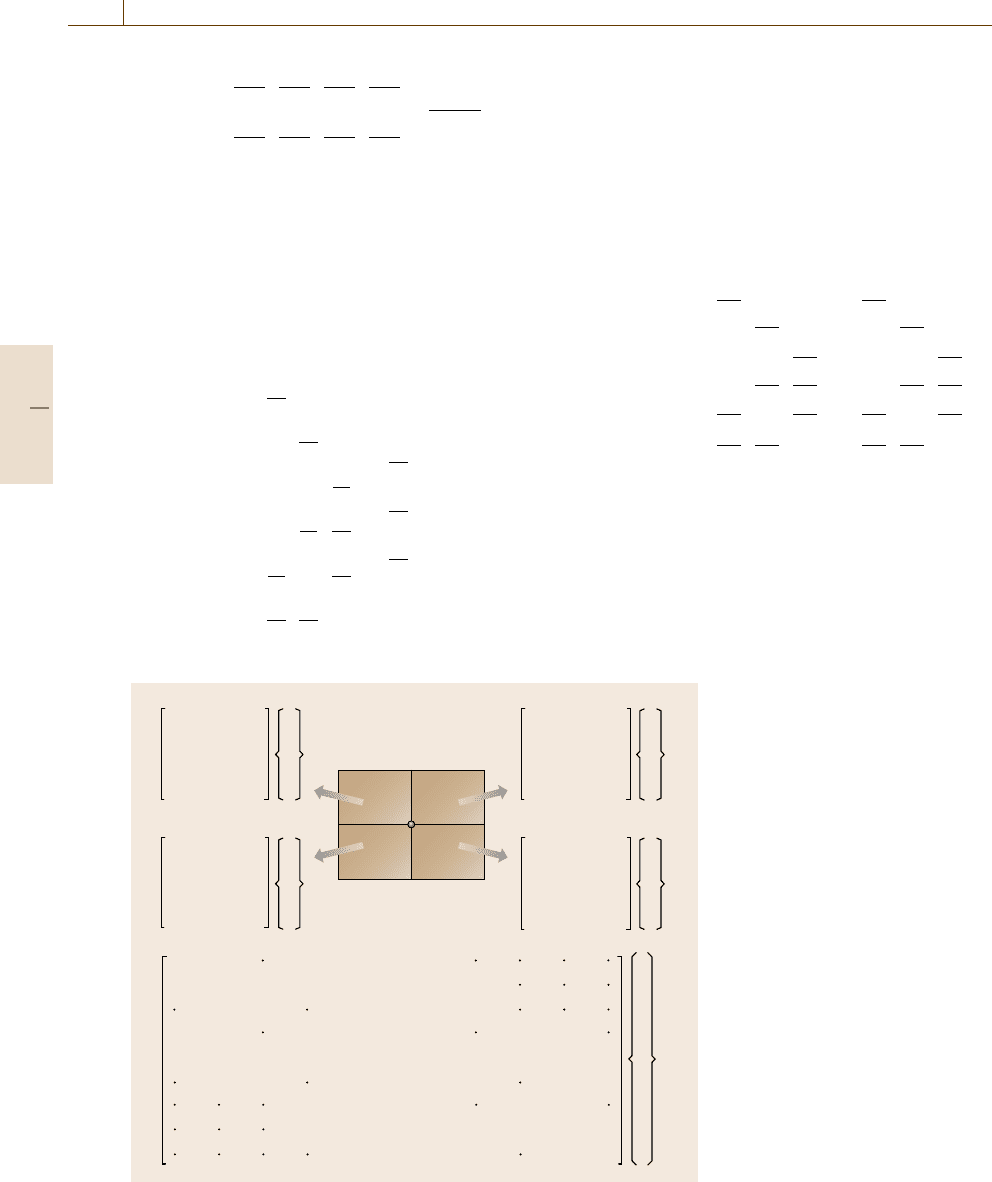
9
6
3
8
5
2
7
4
1
a
11
a
12
a
14
a
15
u
1
u
2
u
3
u
4
u
5
u
6
u
7
u
8
u
9
a
21
a
22
a
24
a
25
a
41
a
42
a
44
a
45
a
51
a
52
a
54
a
55
u
1
u
2
u
3
u
4
c
44
c
45
c
47
c
48
c
54
c
55
c
57
c
58
c
75
c
75
c
77
c
78
c
84
c
85
c
87
c
88
u
4
u
5
u
7
u
8
b
22
b
23
b
25
b
26
b
32
b
32
b
35
b
36
b
52
b
53
b
55
b
56
b
61
b
63
b
65
b
66
u
2
u
3
u
5
u
6
d
55
d
56
d
58
d
59
d
65
d
66
d
68
d
69
d
85
d
86
d
88
d
89
d
95
d
96
d
98
d
99
u
5
u
6
u
8
u
9
d
86
c
88
+d
88
d
89
c
85
+d
85
c
84
c
87
d
95
c
98
d
96
d
99
c
75
c
74
c
77
c
78
b
65
+d
65
b
62
d
68
b
63
b
66
+d
66
d
69
a
52
+b
52
b
53
b
56
+d
56
a
51
a
54
+c
54
c
57
a
55
+b
55
+c
55
+d
55
c
58
+d
48
d
59
a
41
a
44
+c
44
c
47
a
45
+c
45
a
42
c
48
b
33
b
32
b
36
b
35
a
21
a
22
+b
22
a
24
a
25
+b
25
b
23
b
26
a
11
a
12
a
14
a
15
Fig. 19.23 Local and global matrix in
two-dimensional FEM
Considering (19.119), the local stiffness matrix
K
element j
for an eight-node brick element can be defined
as below, where the D matrix is the same as in (19.72)
for the isotropic elastic cases. This is schematic view of
the K
element j
matrix and the treatment in Fig. 19.22 is not
visualized here. For further details, please refer to [19.2].
K
element j
u
element j
=
⎛
⎜
⎝
Ω
j
B
t
DBdΩ
⎞
⎟
⎠
u
element j
where B =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
∂N
1
∂x
00...
∂N
8
∂x
00
0
∂N
1
∂y
0 ... 0
∂N
8
∂y
0
00
∂N
1
∂z
... 00
∂N
8
∂z
0
∂N
1
∂z
∂N
1
∂x
... 0
∂N
8
∂z
∂N
8
∂x
∂N
1
∂z
0
∂N
1
∂x
...
∂N
8
∂z
0
∂N
8
∂x
∂N
1
∂y
∂N
1
∂x
0 ...
∂N
8
∂y
∂N
8
∂x
0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
,
u
element j
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
u
element j
1
v
element j
1
w
element j
1
.
.
.
u
element j
8
v
element j
8
w
element j
8
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
. (19.120)
Part E 19.7
Finite Element and Finite Difference Methods 19.9 Advanced Topics in FEM and FDM 1055
19.8 Treatment of the Nonlinear Case
Nonlinear problems can be classified into several
patterns, such as material nonlinearity, geometrical non-
linearity (including large strain/stress and buckling),
and boundary nonlinearity (including moving boundary
and contact/friction). Since nonlinearity among these
classes is so different on a numerical sense, the reader
should be careful, when using nonlinear commercial
software. Even the defined strain is different in some
settings (for further information, refer to [19.6]).
As for the numerical treatment of the nonlinear
problem, we want to pick up one typical method here.
The Newton–Raphson method [19.4] is the method
used to solve a nonlinear equation g(x) =0 by iterative
calculation of the derivative of g(x) (or Jacobian in the
multidimensional case) as shown in (19.121)
g (x) =0 . (19.121)
By applying a Taylor’s expansion to the nonlinear
iterative equation g
x
k+1
= 0 around x
k
and omitting
higher-order terms, we get
g
x
k+1
≈ g
x
k
+g
x
k
x
k+1
−x
k
=0 .
(19.122)
Rewriting (19.122) results in the following represen-
tation, which drives the k +1th step approximated
solution x
k+1
from the value x
k
at the previous kth step
x
k+1
= x
k
−
!
g
x
k
"
−1
g
x
k
, g
x
k
= 0 .
(19.123)
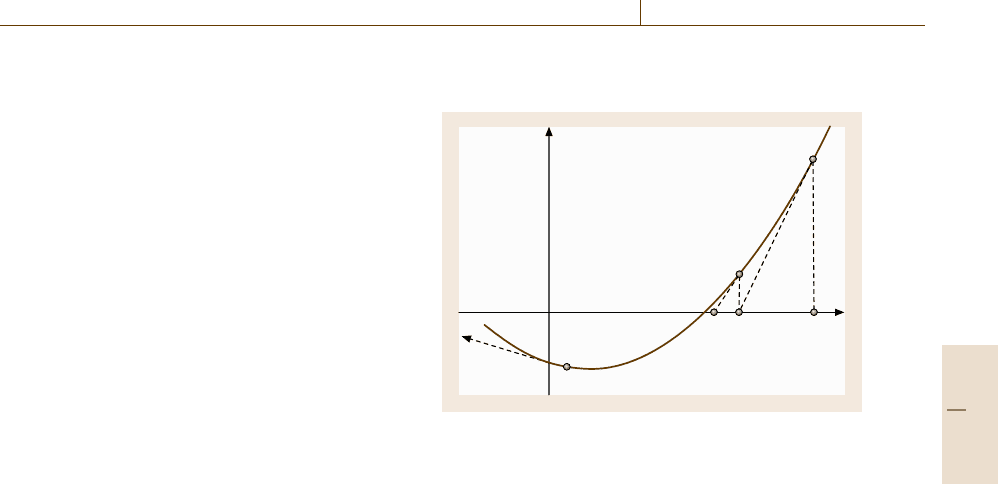
It should be noted that Newton–Raphson method
is valid for multidimensional nonlinear problems as
g(x)
Q
x
*
x
2
x
1
x
0
Fig. 19.24 Newton–Raphson method
shownin(19.124)
g
1
(
x
1
,...,x
n
)
=0 ,
...
g
n
(
x
1
,...,x
n
)
=0 . (19.124)
If the nonlinearity of the equation is not severe and
the initial guess x
0
is not far from the solution, this
algorithm offers a numerically acceptable converged so-
lution x
∗
by applying (19.123) iteratively from an initial
guess x
0
, as shown in Fig. 19.24. However if an initial
guess x
0
is too far from a converged solution x
∗
(for
example, the point Q is selected as an initial guess x
0
in Fig. 19.24) or if the function g(x) =0 is highly non-
linear, the method might still diverge, even after many
iterations. In this case, more stable methods such as the
Riks method [19.6] should be applied.
19.9 Advanced Topics in FEM and FDM
Some advanced topics are treated in this section. You
may encounter some of the problems when you use
FEM or FEM software packages. The explanation be-
low is just a sample for the reader, with references
provided for more information.
19.9.1 Preprocessing
Until now we have been talking about theoretical as-
pects with an algorithm explanation. However, the most
time-consuming part in the numerical analysis (espe-
cially in three-dimensional case) is modeling, which is
the process of making FE mesh or FD grids in advance
of simulation.
Some so-called automatic mesh/grid generator soft-
ware is available, however, the reader should recognize
that there are two categories of automatic model
generation schemes: the interactive mapped mesh half-
automatic generation approach and the noninteractive
nonmapped mesh full-automatic generation approach.
The former requires an interactive, time-consuming
task to help the automatic mesh generation software.
Part E 19.9
1056 Part E Modeling and Simulation Methods
The basic idea of mapped mesh approach [19.8]is
based on the conforming mapped function as shown
in Fig. 19.22a,b.
Since FDM handles regular shaped domains in most
cases because of its limitation, mesh generation is
done using the interactive mapped mesh approach ba-
sically [19.9]. However, FEM can treat the domain of
an arbitrary shape, thus the noninteractive nonmapped
mesh approach might be a better tool for model-
ing [19.10].
It should be noted that the modeling method greatly
affects the quality of solution in discretized meth-
ods. The reader should always recognize that what the
discretized numerical method can do is provide an ap-
proximated solution.
19.9.2 Postprocessing
As mentioned in remark (4) in Sect. 19.2.2,thefirst
derivative of an FE function is discontinuous between
elements. This implies that a node has m derivative val-
ues if the node is surrounded by m elements. To obtain
a representative value at a node, Winslow’s weighted
averaging scheme (19.125) in [19.11]orsuperconver-
gent patch scheme [19.12] is usually applied, which is
nothing but a process to convert element-wise values to
nodal values
x
n
=
)
mj
nj=1
xg
nj
w
nj
)
mj
nj=1
w
j
, (19.125)
where x
n
is the target variable at node n, x
nj
is the
centroid coordinates at finite elements j( j = 1, mj)
connected with the node n,andw
nj
is a weight (1 in
this case) at element j. Visualization software some-
times does this kind of postprocessing automatically,
which can conceal unacceptable unsmoothed solutions
with nice visualizations in some cases.
19.9.3 Numerical Error
If we get some unacceptable numerical results as com-
pared with experimental data, there might be several
causes for the errors. Basically, a numerical simu-
lation involves three stages, as shown in Fig. 19.25.
The major error source might lie between the real
problem and physical model, which is related to the
simplification process of the real target problem with
selecting a proper physical property. For example, if
the head conduction coefficient is improper (inaccu-
Real problem
Real experiment
Simple experiment
Benchmark
Simulation
Physical model
Verification
Validation
Fig. 19.25 Three stages of simulation
rately approximated) to model the considered problem,
we cannot get an acceptable numerical solution even
with very accurate numerical schemes applied. The re-
sponsibility of numerical schemes only covers physical
models and simulation, although it gives rise to serious
error due to an inefficient number of grids or meshes.
To distinguish the discussion between the former and
the latter, the terminology verification and validation
is sometimes used [19.13]. Validation is confirmation
by examination and provisions of objective evidence
that the particular requirements for a specific intended
use are fulfilled, while verification is confirmation by
examination and provisions of objective evidence that
specified requirements have been fulfilled, according to
IEEE definition [19.13]. Thus, in discussion above, the
former is related to validation, while the latter is linked
with verification.
As described above, infinitely fine mesh/grid leads
to the exact solution, which requires an infinite scale
matrix calculation. It is an important idea for engi-
neers to establish acceptable numerical analysis within
the limitation of real computational power available.
Since the quality of FD/FE analysis greatly depends on
the quality of mesh/grid, the reader must be careful in
real simulations. Automatic mesh/grid control schemes,
such as the adaptive finite element method [19.12]
or boundary-fitted finite difference method [19.9], can
be useful for this purpose. Most commercial software
provides this function for better results. It should be
emphasized that this is only related to the verification
stage.
As for the worse cases, solutions themselves can
sometimes not be obtained due to the improper set-
Part E 19.9

Finite Element and Finite Difference Methods 19.9 Advanced Topics in FEM and FDM 1057
tings in numerical analyses. For example, the treatment
of incompressibility in fluids and solids is one of the
typical matters to be noted. In incompressible flows,
the equations for velocity and pressure are usually
solved separately in a weakly coupled fashion. In this
case, the feasible combination of velocity-element and
pressure-element is limited by the Ladyzhenskaya–
Babuska–Brezzi (LBB or BB) condition in the usual
FE formulation [19.14], while staggered-type grids
are needed in popular FD formulation [19.14]. It
should be added that there are no uniform general nu-
merical formulation proposed that are valid for both
incompressible and compressible flows. In the same
manner for fluid, the treatment of incompressible ma-
terials in solid FEA should be carefully treated, which
can be a cause of so-called locking in the simu-
lation. The treatment of magnetic problems usually
needs some techniques. The problems above might
be described in the manuals in most commercial
FE/FD software, but the reader should keep them in
mind.
Usually FEM and FDM are conducted with the in-
formation of material properties, domain’s shape, and
boundary conditions, to obtain the distribution of tem-
perature in thermodynamics, displacement/strain/stress
in solid mechanics, velocity/pressure in fluid dynamics,
and so on. If and only if the quality of the simulation
is highly reliable, material properties can be measured
by applying FEM and FDM iteratively with the tech-
nique of minimum search. This inverse problem setting
is sometimes useful, especially when the direct mea-
surement is impossible for some reason, although the
uniqueness of the inverse solutions is not always guar-
anteed. For information on the state-of-the-art of this
subject, please refer to [19.15].
19.9.4 Relatives of FEM and FDM
There exist other methods categorized in discretized
numerical schemes. We briefly introduce some of
them.
Finite Volume Method (FVM)
FVM is an effective scheme for fluid dynamics, where
flux-balancing is considered in a finite volume (control
volume) [19.16]. The domain is discretized into infinite
number of finite volumes, and its shape can be arbitrary.
Unknown variables are defined at the center of the con-
trol volume, while the flux on its boundary is linked
with the unknown variables in some way.
Boundary Element Method (BEM)
The derivation of BEM is based on Green’s theorem
with the use of fundamental solutions in various phe-
nomena [19.17]. BEM mainly supports linear analysis.
According the Green’s theorem, an n-dimensional prob-
lem can be treated as an (n −1)-dimensional problem
setting but only homogenous material can be handled
in BEM. The main advantage of this method is that it
can treat infinite domain such as in magnetic or acoustic
problems without any theoretical difficulties. The ma-
trix is a dense matrix, while it is a sparse matrix in other
discretized methods.
Constrained Interpolated Profile (CIP) Method
The CIP method is very powerful for moving boundary
problem and multiphysics problems [19.18,19]. It is one
of multimeasure methods with a spline-interpolation
function in FDM’s category, which utilizes both vari-
ables and its derivatives for calculation.
Particle Method
The biggest weak point of discretized methods is that
it cannot easily handle complicated moving bound-
ary unsteady problems, including explosions, since the
topology of grid/mesh must be fixed during time-step
calculations. Particle methods, such as the discrete
element method (DEM), smooth particle hydrodynam-
ics method (SPH), and related various methods, are
good for these unflavored problems. Because of limited
space in this chapter, please refer to [19.20] for details.
Including the additional methods treated above,
a rough summary of the properties of each method is
showninTable19.1. The information listed might be
not a complete set, but serves as a reference for a reader.
19.9.5 Matrix Calculation
and Parallel Computations
As shown above, the coefficient matrix in FEM and
FDM is a diagonal-dominated (banded) sparse matrix.
The matrix can be symmetrical in heat and elastic solid
problem or nonsymmetrical in fluid and nonlinear solid
problems.
There are two categories in matrix calculation: di-
rect method and iterative method. The direct matrix
solvers are based on Gauss-elimination and its mod-
ifications, such as the skyline method for symmetric
matrices, frontal (wave front) method for a nonsymmet-
ric matrix. Since the banded size around the diagonal
varies according to the numbering of the nodes, which
Part E 19.9
