Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing

Подождите немного. Документ загружается.

1018 Part E Modeling and Simulation Methods

controlled stress tests generally exhibit large amounts of

scatter.

The next example is stress response under combined

states of tension and torsion, where a thin-walled tubu-

lar specimen is employed to realize the multiaxial stress.

An out-of-phase strain path with a square pattern is im-

posed on the specimen, as shown on the left-hand side

of Fig. 18.3 [18.18]. The stress components show a com-

plicated trajectory due to the out-of-phase strain path.

Where the strain trajectory has a corner, the stress trajec-

tory suddenly changes in order to follow the normality

rule, and the magnitude of the stress is generally larger

than the normal stress under uniaxial loading. Most of

the constitutive models follow the exact trajectory, and

the performance of the model is due to the modeling

of additional hardening under nonproportional loading.

Since all of the parameters used in constitutive mod-

els are taken from conventional test data obtained under

conditions of uniaxial stress, this particular hardening

behavior cannot be predicted in principle. Multiaxiality

should preferably be introduced in the model while the

parameters are to be simply determined.

18.2 Material Anisotropy

18.2.1 Description of Material Anisotropy

Solids are usually deﬁned in such a way that the

material has a reference conﬁguration and that a re-

sistance to deformation occurs. If the resistance of

the material depends on the direction, the mater-

ial is said to be anisotropic, while it is said to

be isotropic if the same response is observed for

any direction. The anisotropy is characterized by the

existence of so-called anisotropic axes or preferred

orientations in material. There are various classes

of anisotropy, such as orthotropy, planar anisotropy,

and so on. Here we summarize a rational method of

obtaining a concrete form of an anisotropic consti-

tutive equation based on the representation theorem

for isotropic tensors [18.19]. Here it should be noted

that the term isotropic tensor means an objective ten-

sor that is independent of a change of frame; in

other words isotropic means something very differ-

ent here to when we use it in relation to isotropic

and/or anisotropic material properties. Figure 18.4 de-

scribes the fundamental concept of material anisotropy.

Let m

(1)

, m

(2)

... be vectors lying along the aniso-

tropic axes, whose components are given by m

(k)

(k = 1, 2 ...) under a particular orthonormal basis e

For example, three kinds of anisotropic axes exist in

orthotropic materials, which are mutually orthogonal.

Without any loss of generality we can assume that each

(1)

(2)

(3)

Fig. 18.4 Basic

concept of ma-

terial anisotropy

vector is a unit vector and therefore the following rela-

tionship holds

(1)

(2)

(3)

=δ

. (18.22)

Here δ

stands for the Kronecker delta.

Any tensor function used in continuum mechanics

must fulﬁll the principle of objectivity. This requires the

components to be invariant under the orthogonal trans-

formation Q

. Suppose that a tensor T

ij···k

is expressible

as a function with p sets of vectors u

(p)

and q sets of

second-order tensors U

(q)

.Thenitisexpressedas

···Q

lm···n



(p)

, U

(q)



= T

ij···k



(p)

, Q

(q)



. (18.23)

The orthogonal transformation of a vector and a second-

order tensor takes the form

(p)



(p)

, (18.24)

(q)



(q)

. (18.25)

Using the representation theorem for isotropic tensors

discussed by Spencer [18.19], a second-order symmet-

ric isotropic tensor function can be reduced by taking

the derivative of a scalar such that

∂I

∂K

. (18.26)

Here the scalar function indicates an invariant scalar

with arguments that is linear on a symmetric tensor K

The scalar I is expressed as

I =φ

+···+φ

, (18.27)

Part E 18.2

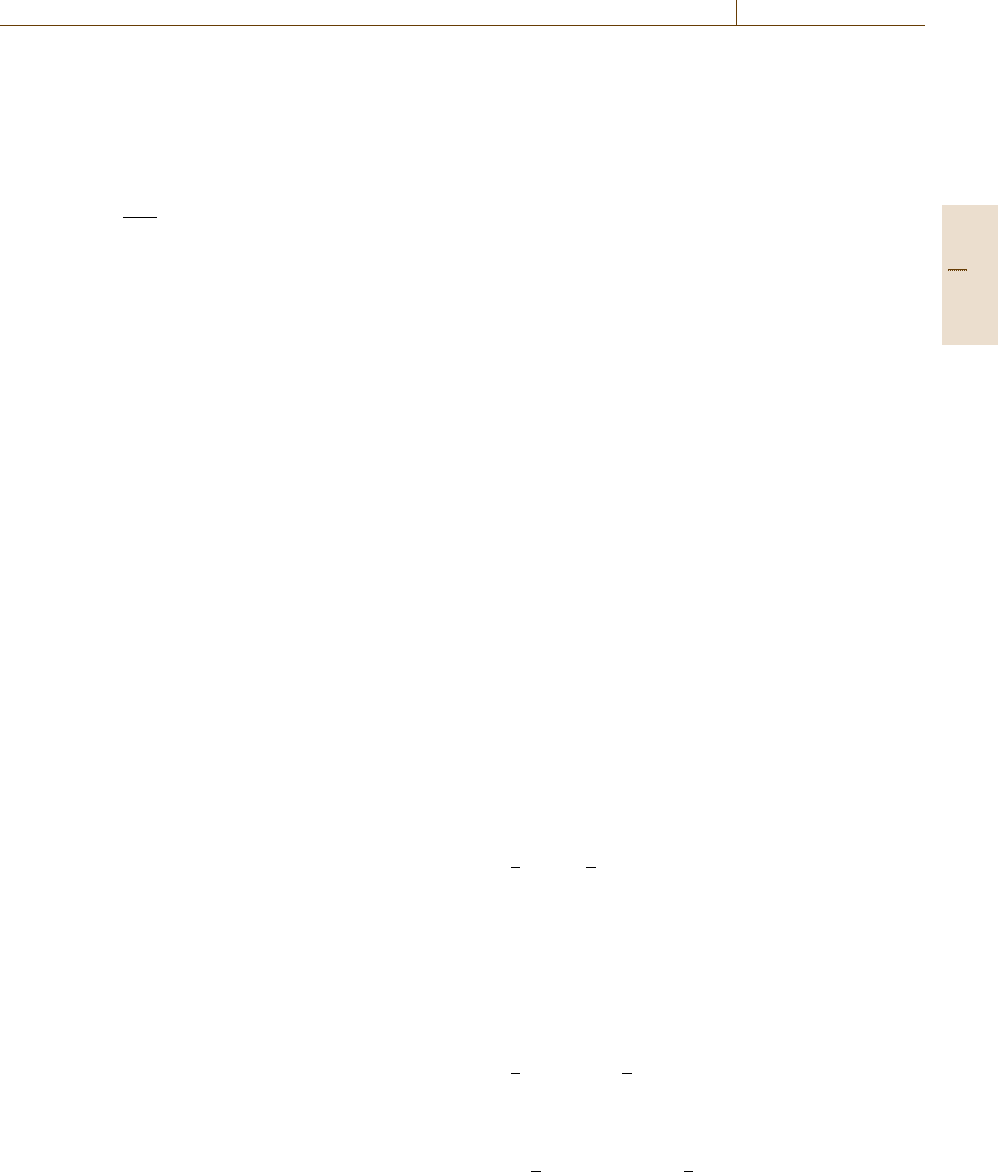
Continuum Constitutive Modeling 18.2 Material Anisotropy 1019

where J

stands for invariants that are linear on K

to-

gether with arguments U

(p)

and u

(q)

; φ

are coefﬁcients

expressed as polynomial functions of the invariants of

(p)

, u

(q)

and possible combinations of them. In this

case (18.26) can be rewritten in the form



s=1

∂J

∂K

. (18.28)

The full list of invariants with vectors, symmetric ten-

sors, and skew-symmetric tensors can be found in the

literature [18.19, 20]. Isotropic tensors are express-

ible as multilinear forms of the arguments using this

technique.

When we take a symmetric tensor A

as an argu-

ment, the scalar I with K

is expressed by

I =φ

+φ

. (18.29)

A second-order symmetric isotropic tensor with one

kind of argument is then given via (18.28)by

=φ

+φ

, (18.30)

where φ

(r = 1, 2, 3) denote scalar coefﬁcients which

are also polynomial functions with the invariants of A

When we adopt the second Piola–Kirchhoff stress ten-

sor in T

and the Green strain tensor in A

,(18.30)

leads to the most general representation for a hypere-

lastic material. When we pick a special representation

which is linear on A

,(18.30) is reduced to

=φ

+φ

, (18.31)

where φ

(r = 1, 2) are now constant. When we re-

gard the Cauchy stress as T

and the inﬁnitesimal strain

as A

, this coincides with the linear elasticity constitu-

tive equation

= E

ijkl



λδ

+2μδ



, (18.32)

where φ

have been replaced by Lame’s constants λ and

μ.

For the anisotropic elasticity model, the scalar I

involves a second-order symmetric tensor A

and

skew-symmetric tensors X

. Since any skew-symmetric

tensor can be characterized by an axial vector m

using

the relationship

=ε

ijk

(18.33)

we can add vectors in deducing the full represen-

tation of general anisotropic materials. In the case

of planar anisotropy, where one kind of vector lies

perpendicular to the plane, we have ﬁve material pa-

rameters among the elasticity constants [18.20]. In

the most general aniotropic materials within the lin-

ear formulation, we have 21 constants because of

the following condition imposed on the elasticity

constants

ijkl

= E

jikl

= E

ijlk

= E

klij

. (18.34)

No other condition is imposed on the material param-

eters.

18.2.2 Initial Anisotropy

Next we discuss the mathematical formulation of

plasticity models accounting for initially anisotropic

materials that (mainly for simplicity) initially exhibit

orthotropy. When materials – particularly ductile metal-

lic materials – deform under certain conditions, the

anisotropic axes may change direction. They may not

then be mutually orthogonal, even though they were

orthogonal in the initial state. The evolution of the

anisotropic axes, if the anisotropic vectors are embed-

ded in the material, takes the form

−W

= D

, (18.35)

where

m means the Jaumann rate of the vector m. D

and W are the stretching tensor and spin tensor respec-

tively. It should be noted that this form is just one of

the possible forms, and we do not exclude other formu-

lations. If the orthotropy is maintained throughout the

deformation, another type of evolution may be prefer-

able.

A typical yield function for isotropic materials reads

F =



−

=0 . (18.36)

Here σ



denotes the deviatoric part of the stress

and

refers to the yield stress. One general-

ized form with a quadratic yield function was pro-

posed by Hill [18.21], where a fourth-order ten-

sor reﬂecting material anisotropy plays a central

role

F =

ijkl

−

=0 . (18.37)

When N

ijkl

takes the form

ijkl



+δ



−

, (18.38)

Part E 18.2

1020 Part E Modeling and Simulation Methods

a) Isotropy

b) 0° c) 45° d) 90°

0.3

R.D.

0.2

0.1

0.6

0.1

0.5

0.4

0.3

0.2

R.D.

0.1

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.5

0.4

0.3

0.2

0.1

R.D.

e) 45°

Fig. 18.5a–e Strain localization behavior of a rolled sheet for various stretch directions

(18.37) is reduced to (18.36). When N

ijkl

involves m

(1)

and m

(2)

, the fourth-order tensor takes the form

ijkl

=λ

(δ

+δ

)+λ

(δ

)

−

(δ

+δ

)

(δ

)

−

(δ

+δ

)

) ,

(18.39)

where a

, a

,anda

are material parameters with the

following symbols

(1)

−

(1)

, (18.40a)

(2)

−

(2)

. (18.40b)

When the norm of the anisotropic vector is kept unitary,

the above formulations become slightly simpler because

(p)

= 1(p =1, 2). Suppose that the anisotropic

axes coincide with the base vector, so that they are

(1,0,0) and (0,1,0) for example; in this case we can

prove that (18.37) is completely identical to Hill’s

original model. Since the anisotropic axes change direc-

tion during deformation, it is preferable to generalize

the representation so that it is applicable to general

anisotropy, and this can be done by introducing a more

general fourth-order tensor.

In order to examine the effect of initial anisotropy,

ﬁnite element analysis is implemented based on the up-

dated Lagrangian (U-L) formulation [18.22]. In the U-L

formulation, the stress in the constitutive law is regarded

as the Jaumann rate of the Kirchhoff stress and the strain

rate as the stretching. The balance equation is based

on the equilibrium under the Lagrangian system at the

current state and the rate-type formulation is employed

for this elastic-plastic boundary value problem. This

implies that the rate of Lagrange stress is equilibrated

and related to the Jaumann rate of the Kirchhoff stress.

Converting these terms into discrete levels, we have





tan

−F)B+E

QE]dV





t dS (18.41)

for the ﬁnite element stiffness in the rate-type formula-

tion. Here N, B and E are the shape function, the strain–

displacement matrix and the velocity gradient matrix; F

and Q are compensation terms due to U-L formulation,

and the body force is neglected for simplicity. The sim-

Part E 18.2

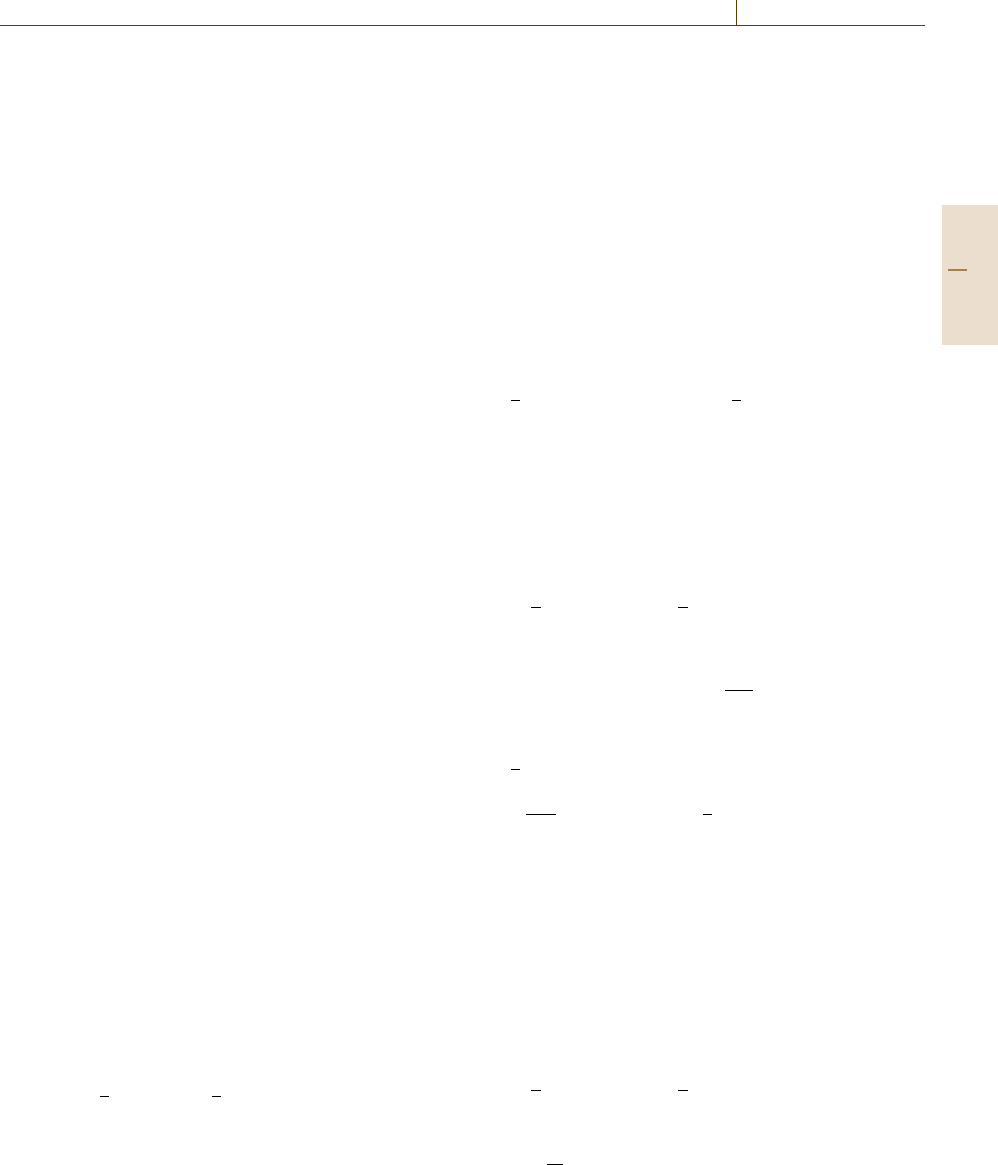
Continuum Constitutive Modeling 18.2 Material Anisotropy 1021

ulation proceeds step-by-step by solving the stiffness

equation to unknown nodal displacement rate

Figure 18.5 demonstrates the necking behavior of an

initially orthotropic sheet [18.23]. A three-dimensional

simulation was carried out since the anisotropic vectors

could change direction during the course of deforma-

tion. The material parameters are obtained from data

on carbon steel sheets. The ﬂow stress in a steel sheet

is the lowest in the rolling direction (RD)andthe

highest in the perpendicular direction, while aluminium

sheets show an opposite tendency. Figure 18.5ashows

simulated results for isotropic material, and the last

photograph corresponds to the results of a uniaxial rup-

ture test performed at 45

◦

to the rolling direction. The

higher the strain concentration, the lower the tensile

stress. This implies that the strain concentration in b

and c are reasonable, and that the onset of strain lo-

calization is affected by the ﬂow stress in the tensile

direction. Figure 18.5b shows a characteristic aspect

of strain localization where the localization appears in

a band inclined to both the rolling direction and the ten-

sile direction. The same tendency is also observed in the

experiment.

18.2.3 Induced Anisotropy

The Bauschinger effect is a phenomenon where ma-

terials later show anisotropy even when they exhibit

isotropy in the initial state. The kinematic hardening law

is useful for dealing with this type of anisotropy. In this

case, the yield surface is translated in stress space while

the shape is not changed. Another type of anisotropy as

well as this one is usually found in experiments, called

the cross effect or the corner effect according to pio-

neering work by Phillips [18.24]andIkegami [18.25].

Several models have been proposed so far to describe

the subsequent anisotropy, which can be roughly classi-

ﬁed into two categories

(A) Where the yield function includes higher order ten-

sors representing the anisotropy, as discussed in

the previous section. Baltov and Sawczuk [18.26]

proposed a model based on Hill’s quadratic yield

function [18.21], and other researchers [18.27, 28]

have also employed this concept. The models are

simply expressed by

F =

ijkl

−

=0 . (18.42)

(B) The other type of formulation assumes that the yield

function is composed of the combination of the sec-

ond and third invariants of the stress J

and J

This procedure was proposed by Drucker and

Prager [18.29]. A typical representation [18.30]

takes the form

F = J

−



−

=0 . (18.43)

Here ξ

,... express the inelastic deformation his-

tory.

The former is superior to the latter from the viewpoint of

parameter identiﬁcation because (18.43) provides lots

of possibilities for the concrete representation of power

factors. Taking into account the back stress concept,

(18.42) can be modiﬁed to

F =

ijkl

(σ

−α

)(σ

−α

) −

=0 (18.44)

and the kinematic back stress α (or equivalently the

plastic strain when employing the Prager hardening

rule) and additional variables are introduced into the

fourth-order tensor N

ijkl

. When the fourth-order ten-

sor involves one kind of second-order tensor ξ

1ij

,the

fourth-order tensor N

ijkl

is simply expressed by

ijkl

(δ

+δ

) −

+ P

1ij

1kl

(18.45)

In order to justify the physical dimension we add the

nondimensional back stress: ξ

1ij

√

3/2α



. The ﬁ-

nal form of the yield function is

F =



−α







−α









−α









−

=0 (18.46)

although the fourth-order tensor is not a full rep-

resentation. This yield function is identical to the

Baltov–Sawczuk yield function [18.26] and it describes

elliptical shapes with the yield as locus with the de-

velopment of ξ

1ij

(the kinematic back stress α

plastic strain ε

). In order to describe higher order dis-

tortions [18.31] such as the cross effect, we introduce

another kind of second-order tensor ξ

2ij

into the repre-

sentation of N

ijkl

, and then we have

ijkl

(δ

+δ

) −

+ P

1ij

ikl

2ij

2kl

(ξ

1ij

2kl

+ξ

2ij

1kl

) . (18.47)

Part E 18.2

1022 Part E Modeling and Simulation Methods

–1.5

Dimensionless axial stress σ'

Dimensionless shear stress τ'

21.51.10.50–0.5–1

–1

–0.5

0.5

1.5

Present model

= 1 Q = 1

Baltov–Sawczuk model

= 1 Q = 0

' = 0 α

' = 00.7 1

Fig. 18.6 Descriptions of higher order anisotropy for the cross ef-

fect and the corner effect

–300

Axial stress σ (MPa)

Shear stress √3 τ (MPa)

300–200 –100 0 100 200

–400

–300

–200

–100

100

200

300

117

150

180

160

0.0

80.5

62.0

1.2

0.4

Analytical Experimental

= 0.6

Q = 1.3

= 0

(MPa)

(%)

(MPa)

Fig. 18.7 Yield loci under monotonic tension

Here we adopt a nondimensional stress deviator in ξ

2ij

Finally the following yield function is obtained

F = (S

− A

)(S

− A

) +P

[(S

− A

]

+ P

[(S

− A

]

+Q[(S

− A

][(S

− A

]−1 =0 ,

(18.48)

where we have

1ij





≡ A

, (18.49a)

2ij





≡ S

, (18.49b)

for simplicity. In terms of choosing parameters, P

dominant for the Bauschinger effect, P

= 0 ensures

initial isotropy, and Q is related to the description

of the cross effect. Since the second-order tensors

adopted in the model reﬂect the current state of back

stress and stress deviator, particular anisotropy with the

path/history dependence can not be described by the

model.

Figure 18.6 shows the basic performances of the

yield functions [18.31] and the variation in yield locus

is shown for a combined tension–torsion stress state,

in which the axial and shear stresses are displayed in

nondimensional ways such that the values are normal-

ized by the yield stress. Dashed lines exhibit elliptical

shapes given by the Baltov–Sawczuk theory, while the

solid lines show the results from the higher order the-

ory used to describe the cross effect, which exhibits

characteristic hardening backward and perpendicular to

the tensile direction. As the deformation increases, the

kinematic back stress increases and then the ellipti-

cal shape shrinks towards the tensile direction. Since

the deformation shown in the ﬁgure corresponds to

a uniaxial stretch, the yield loci can be determined

experimentally.

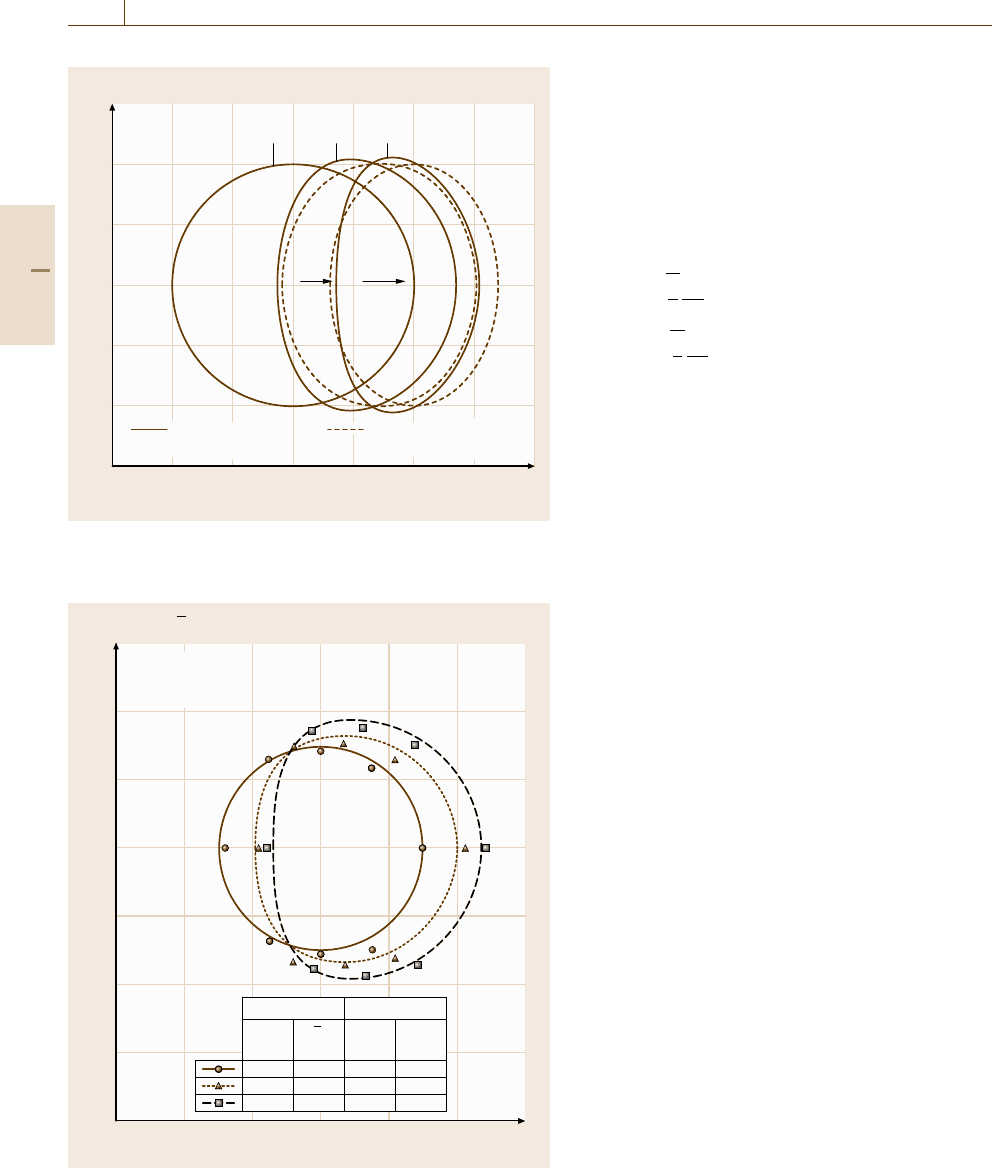
Experimental veriﬁcation was performed on stain-

less steel at an elevated temperature, as shown in

Fig. 18.7 [18.31]. Small cyclic loadings under combined

tension and torsion were performed as uniaxial tension

was applied, and the subsequent yield stresses for these

small cycles were measured. The 304 stainless steel

shows both kinematic hardening and isotropic harden-

ing, and the parameters are chosen to obtain best ﬁt

curves for the yield loci. The development of defor-

mation enhances the anisotropy while expanding the

yield locus. The yield locus in particular expands back-

ward and perpendicular to the loading direction. The

Part E 18.2

Continuum Constitutive Modeling 18.3 Metallothermomechanical Coupling 1023

model successfully describes the development of this

kind of higher order induced anisotropy. However, when

one wishes to include the history effect of asymmet-

ric shape and the corner effect at the loading point,

this model is of no use because it involves current

values of stress and back stress. This problem can be

overcome introducing a multisurface model in stress

space [18.32].

18.3 Metallothermomechanical Coupling

18.3.1 Phase Changes

Engineering processes involving temperature changes,

such as casting, welding, heat treatment and so on,

are widely used to produce materials and improve

their strength and/or functions. In such cases varia-

tions in temperature and internal structure dominate

the dimensional accuracy of and residual stresses in

the ﬁnal product. Any metallic material has a spe-

ciﬁc structure, known as a phase, under certain

conditions of stress, temperature and so on, which

is virtually stable for small disturbances. Carbon

steels have perlite and bainite structures at room

temperature when they are produced via moder-

ate heat treatment processes. On the other hand,

when they undergo rapid cooling from high temper-

atures, the phase changes from austenite to marten-

site, and the martensitic structure is quasi-stable at

room temperature. Quite a large volumetric change

is involved during the quenching process, inducing

residual stresses. This implies that temperature, inter-

nal structure and stress/strain are all coupled together.

Metallothermomechanical coupling theories have been

proposed to deal with such processes [18.33–35].

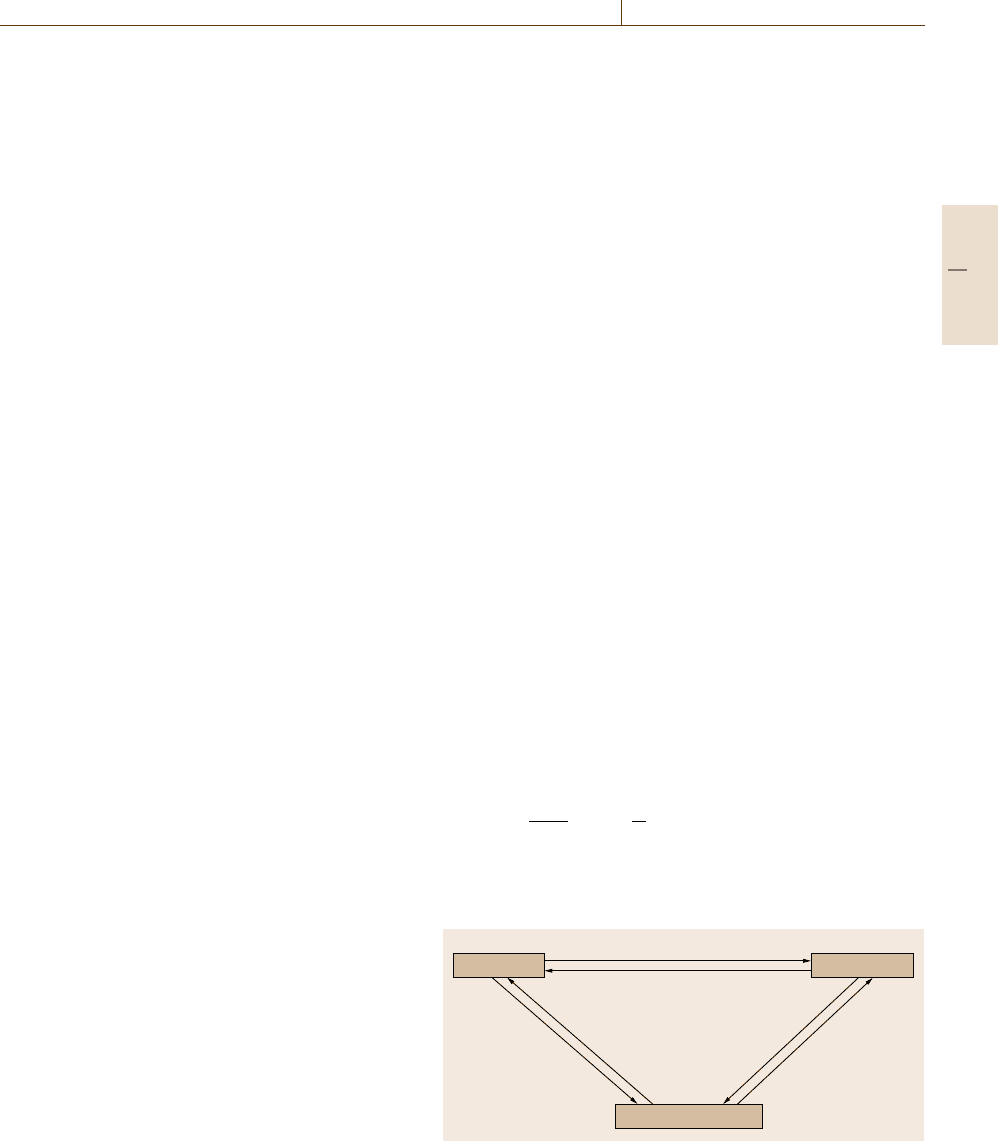
Figure 18.8 illustrates the interactions between tem-

perature, structure and stress [18.36]. When the tem-

perature changes during a process, thermal stresses

(1) are induced, while the metallic phase may also

change (2) depending on the conditions. Stress and

strain are also inﬂuence the temperature (3) due

to plastic mechanical work, while they also inﬂu-

ence the onset of phase change (6). Mechanical

properties are obviously affected by the internal struc-

ture, and the volumetric change due to a phase

change is a typical example of how to affect the

stress/strain ﬁeld (5). Latent heat (4) is generated dur-

ing the phase change, which affects the temperature

ﬁeld.

Based on the mixture theory concept [18.37], a sim-

pliﬁed model has been proposed for dealing with

such complicated processes. Here we regard a par-

ticle at point x as being occupied by a number of

components, namely 1, 2,... and N. The material

properties and/or physical quantities φ of the particle

are assumed to be average values based on the lever

rule

φ =



I=1

. (18.50)

Here φ

is the property of the I-th constituent and ξ

indicates the volume fraction of the I-th component.

Generally the following relationship holds for the vol-

ume fractions



I=1

=1 . (18.51)

This means that one of the N volume fractions is not

derived independently but is automatically given by

the above equation. Using this simple idea, a conven-

tional thermoelastoplasticity theory can be extended

into a theory that accounts for metallothermomechan-

ical coupling.

The thermoelastic theory is formulated as follows

[18.38, 39]. The elastic strain is expressed in terms of

stress, temperature and the volumetric change in struc-

ture, and these contribute linearly to the strain. For

macroscopically isotropic materials, this is expressible



1+ν

−



+α

(

T −T

)



βξ

δij . (18.52)

(T) Thermal stress

Temperature Stress (strain)

Metallic structures

(3) Heat generation due to

mechanical work

(2)

Temperature-

dependent phase

transformation

(4)

Latent

heat

(6)

Stress-induced

transformation

(5)

Transformation

stress

Fig. 18.8 Interaction diagram for thermometallomechanical cou-

pling

Part E 18.3

1024 Part E Modeling and Simulation Methods

Here E and ν are the Young’s modulus and Poisson

ratio of the material. α is the thermal expansion co-

efﬁcient, and β

is the dilatation parameter due to the

change in the I-th constituent. The variation in the tem-

perature T plays an important role here. The elasticity

parameters and thermal expansion are averaged, and the

average values are calculated through (18.50). Taking

into account the mechanical work done due to inelastic

(plastic) work and the latent heat generation, the heat

conduction equation is given by

ρc

∂T

∂t

∂

∂x



∂T

∂x



+σ



, (18.53)

where ρ, c and k are the mass density, the speciﬁc heat

and the thermal conductivity of the mixture, which are

also averaged in the sense of (18.50). Clearly the me-

chanical work from the second term is only generated

during the process of inelastic deformation, and the la-

tent heat of the third term is only dominant when a phase

change occurs. The last two factors can be regarded as

macroscopic heat generation terms. The conventional

plasticity theory is also modiﬁed to a generalized form.

When we employ the von Mises yield criterion with

isotropic hardening, the yield function takes the form

F =



−

(κ, T,ξ

)

=0 , (18.54)

in which the yield stress under uniaxial stress involves

not only a hardening parameter κ, such as the equivalent

plastic strain, but also the temperature T and even the

volume fraction ξ

of each constituent. In order to ob-

tain the current stress, temperature and structures, these

equations are implemented in incremental calculations,

so the rate-type formulation is employed and adopted in

the numerical scheme.

Increment of time

Δt

i+1

Calculation of temperature

increment (ΔT)

i+1

by (Δσ)

Δt

, (Δε)

Δt

, (Δξ

)

Δt

Calculation of stress and

strain increments

(Δσ)

Δt

i+1

, (Δε)

Δt

i+1

by (ΔT)

Δt

i+1

, (Δξ

)

Δt

Calculation of volume

fractions increment (Δξ

)

Δt

i+1

(ΔT)

Δt

i+1

, (Δσ)

Δt

i+1

, (Δε)

Δt

i+1

Fig. 18.9 Numerical algorithm for solving the coupled system of

equations

The kinetics of phase transformation is another

issue to be discussed. Typical phase transformations

in metallic structures include austenite–perlite, fer-

rite, martensite and bainite transformations [18.40–42].

These solid–solid phase transformations are classiﬁed

into two or three categories: the diffusion-driven phase

transformation, the nondiffusion-driven type transfor-

mation, and a mixture of them. The perlite and ferrite

phase transformations are characterized by the ﬁrst cat-

egory, while the martensite transformation falls into the

second category. Here we summarize typical evolution

laws for volume changes due to phase transformations.

The dependence of phase transformations on stress in-

volves another topic called transformation plasticity,in

which permanent deformation is induced by low stress

levels. However, we will not discuss this topic here; in-

stead we limit our discussions to the kinetics associated

with phase changes.

Johnson and Mehl [18.43] proposed the follow-

ing volume fraction for the phase transformation from

austenite to perlite

=1−exp(−V

) . (18.55)

Here ξ

refers to the perlite nucleated from the austen-

ite. ξ

is the volume fraction of austenite, while V

stands for the residual volume of austenite, which is

expressed by



(t −τ )dτ. (18.56)

Here

S and R are the rates of nucleation and growth

respectively. It is assumed in this theory that nuclei are

spherical. The integrand is affected by both temperature

and stress, and so we have



f (T,σ

) ·(t −τ)dτ. (18.57)

The material function f (T,σ

) can be speciﬁed from

a so-called T–T–T diagram (or S-curve) under vari-

ous stress states (pressures). The phase transformation

therefore depends on both stress and temperature, and

the volume change affects the stress ﬁeld due to the

changes in parameters, while the latent heat inﬂuences

the heat conduction.

There are also several models for the process

of martensite transformation, and a phenomenologi-

cal treatment proposed by Magee [18.44] is introduced

here. The martensite transformation starts at a point M

Part E 18.3

Continuum Constitutive Modeling 18.3 Metallothermomechanical Coupling 1025

where two phases have different free energy levels. This

is due to the characteristics of nondiffusion-type phase

transformation. Combining the stress-induced terms,

the volume of martensite ξ

is given by

=1 −exp



−T ) +φ

+φ

1/2



(18.58)

Here φ

, φ

and φ

are material parameters. The tem-

perature is dominated by the ﬁrst term while the mean

stress and the deviatoric stress also affect the marten-

site transformation. If a perlite phase ξ

exists at the

onset of martensite transformation, the above equation

is modiﬁed to

=(1 −ξ

)



1 −exp



−T ) +φ

+φ

1/2





(18.59)

This means that only the austenite contributes to the

nucleation of martensite. These are typical kinetics

equations of solid–solid phase transformations. As well

as these equations, one has to consider solid–liquid

transformation when dealing with welding and casting.

In this case, however, one must return to the original

idea that any material parameter is given in an averaged

manner, because the constitutive equation of liquids is

completely different to that of solids, and the shear vis-

cosity is generally much smaller in liquid.

18.3.2 Numerical Methodology

It is important to ﬁnd an efﬁcient procedure that can be

used to solve the process of thermometallomechanical

coupling in a system. The mechanical equations com-

prise a set of elliptic-type differential equations, while

thermal conduction is governed by a typical diffusion

(parabolic) equation. The kinetics of phase transfor-

mation are also given explicitly. This implies that the

temperature and stress/strain are solved using a ﬁnite

element/ﬁnite volume method, while the variation in

internal structure can be taken into account using in-

ternal state variables. In order to obtain the numerical

solution step-by-step, a suitable algorithm needs to be

constructed. Using simple estimation of the sensitivity

to each term, it becomes clear that thermal conduction

is generally dominant, and that the time step should be

controlled with reference to the thermal conduction if

the mechanical equation is based on quasi-static mo-

tion. The next greatest inﬂuence is the effect of a phase

change on the stress/strain response. Using this, the fol-

lowing numerical scheme can be established.

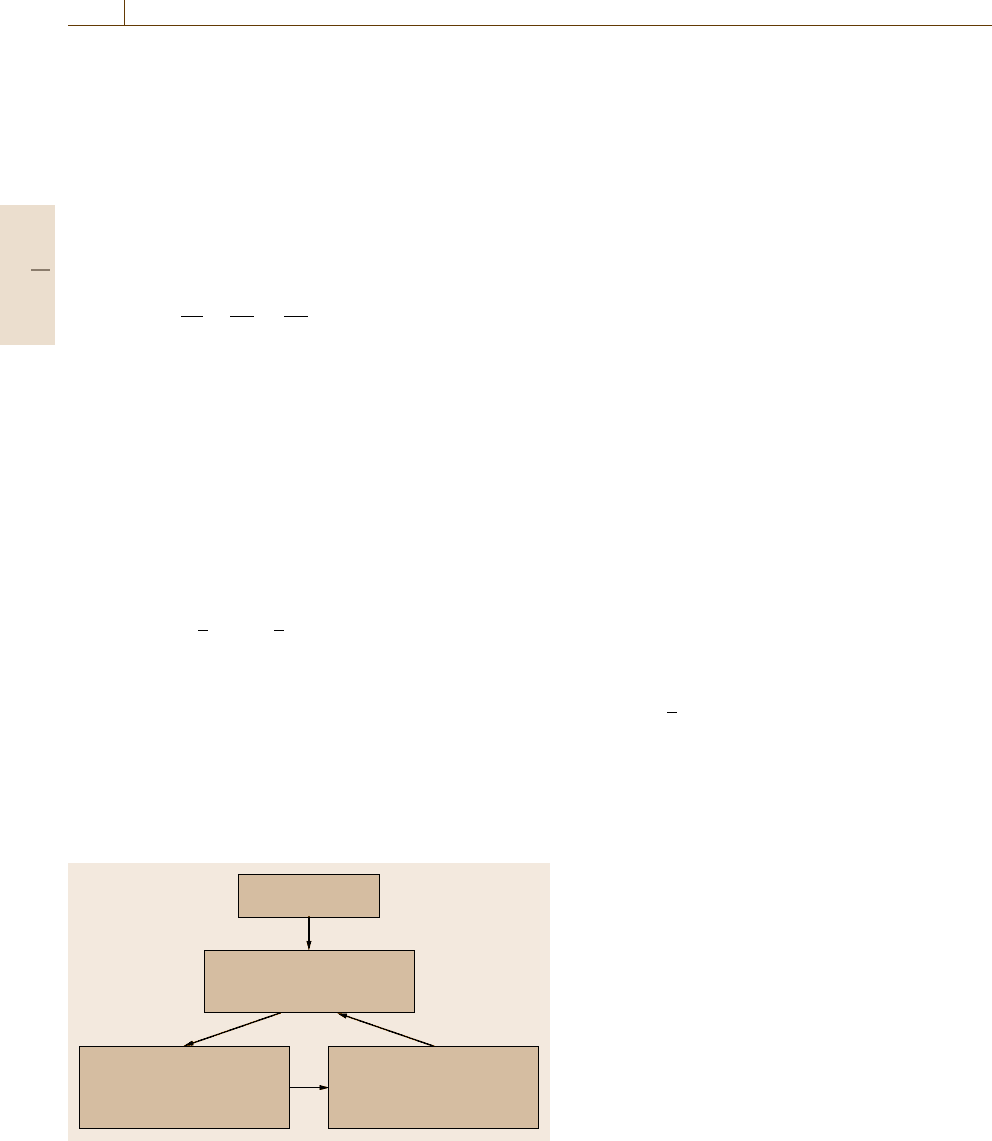
A schematic of the algorithm is shown in Fig. 18.9

[18.36]. Let Δt be the time increment prescribed on an

object. The temperature is ﬁrst updated using the solu-

tion for ΔT where ΔT is obtained using only the values

at the current time step t

. The time increment Δt is small

enough to obtain a stable solution for the temperature.

Using this temperature increment ΔT , the kinetics are

then updated and the volume fractions Δξ

are modiﬁed

during the time increment Δt. Since the change in the

volume fraction affects the stress/strain ﬁeld, the stress

and strain are calculated, with the temperature variation,

last of all. When the mechanical equation is solved for

dynamic motion, substeps with smaller time increments

are superimposed on the time step Δt [18.39]. Although

this iterative process should proceed until the solution is

converges from one time step t

to the next t

i+1

, reason-

able solutions can be found even when the calculation

only passes through each step once.

18.3.3 Applications to Heat Treatment

and Metal Forming

Thermometallomechanical coupling simulations have

been applied in the ﬁelds of heat treatment, welding,

casting and so on, which have the greatest need for di-

mensional accuracy and to know residual stresses. For

example, when a steel is rapidly cooled from a high-

temperature austenitic state, the structure changes to

martensite below the M

transformation state. The vol-

ume increases during this process due to dilatation,

which generally induces compressive stresses. We now

demonstrate a few examples of this from the ﬁeld of

metal forming.

The austenitic stainless steel type SUS304 has a char-

acteristic feature where the austenite at room temper-

ature is said to be quasi-stable and transformed into

martensite under large inelastic deformation. This im-

plies that the stainless steel shows phase transformation

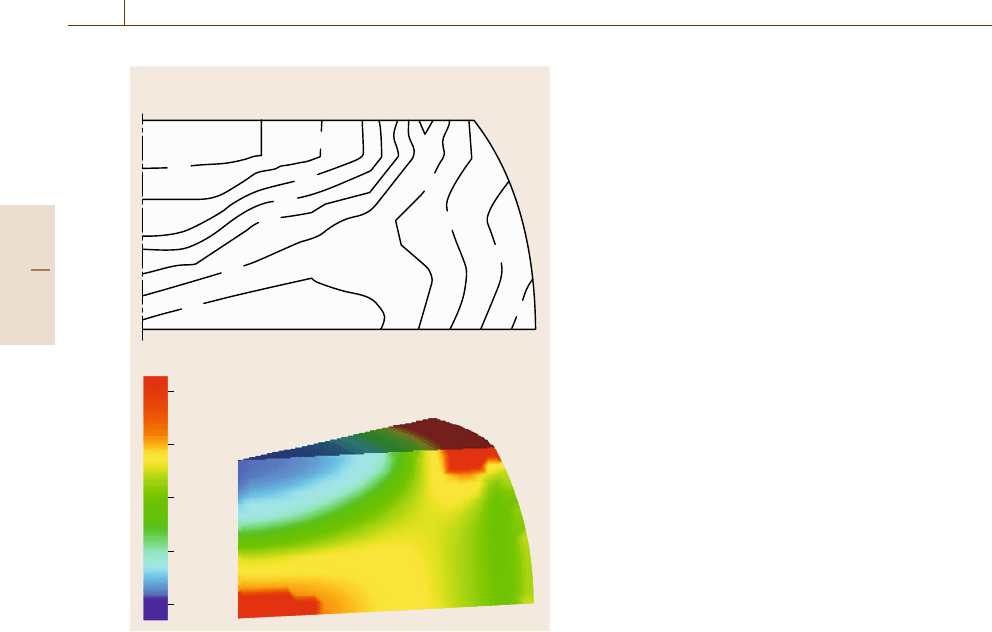
during the course of forming. Figure 18.10 shows the

volume fraction of the martensite during a stamping pro-

cess [18.39]. A rigid die pushes down from the top of the

object, which generates friction between the die and the

material. The upper ﬁgure shows experimental data for

the volume of martensite in % [18.45], while the lower

ﬁgure corresponds to simulated results. The distribution

of the martensite structure observed is caused by both the

deformation and the rate of deformation, while the ther-

mal conditions also inﬂuence the structural distribution

to some degree. Due to the constraints from the friction

between the die and material, the center of the top of

the material is almost ﬁxed and so less deformation is

Part E 18.3

1026 Part E Modeling and Simulation Methods

a) Vo l ume fraction of martensite (%) – experimental

b) Vo l ume fraction of martensite – calculated

0.660

0.495

0.330

0.165

Fig. 18.10a,b Experimental and calculated martensite vol-

ume fractions caused by stamping

induced here during the process. The martensite distribu-

tion in the experiment is obtained by a coupled usage of

magnetic measurement and x-ray diffraction. The simu-

lation successfully grasps the martensite transformation

and shows a good agreement in tendency with the exper-

imental ones.

The advantage of using this type of simulation is

that the temperature, stress/strain and metallic struc-

ture can be obtained at any time. The next example,

shown in Fig. 18.11, demonstrates the effect of friction

on the internal structure and the rate of forming on

the stress level [18.46]. The upper ﬁgures indicate the

residual martensite structure after the forging. The left

side (Fig. 18.11a) shows the martensite structure when

a small friction coefﬁcient (0.1) between the die and

material is used, and the right-hand side (Fig. 18.11b)

corresponds to a larger friction coefﬁcient of 0.2. Since

larger shear stress is induced when overcoming the resis-

tance from the die with larger friction, we expect more

strain to be generated, particularly at the teeth of the die.

This implies that more martensite appears around the

bottom of the teeth. The simulated equivalent stress dis-

tributions for the ﬁrst stroke with a friction coefﬁcient of

0.1 during high strain rate and low strain rate forging are

depicted in the lower parts of Fig. 18.11c, d. The marten-

site distributions in both of these cases at this stage are

similar and small values are obtained. The stresses for

a high strain rate are higher than the stresses for a low

strain rate from the beginning of the stroke until the end

of the loading stage shown in Fig. 18.11c, d. During this

period, the hardening behavior of the material is deter-

mined mainly by austenite, since the martensite content

is low. However, with the generation of martensite, the

ﬂow stress becomes strongly dependent on the marten-

site fraction in the material. The low strain rate produces

much higher stresses at the end of the simulation due to

larger amounts of martensite.

18.4 Crystal Plasticity

18.4.1 Single-Crystal Model

The phenomenological plasticity models discussed so

far have been successful used to describe various

classes of material behavior, not only for complex

loading histories but also for nonisothermal conditions

with varying temperature. However, we have not yet

discussed the real physical mechanism of crystal de-

formation, and so this has not been reﬂected in the

models. Real plastic deformation is mainly caused by

slip in grains, as was pointed out from a continuum me-

chanics viewpoint by Taylor [18.47]andHill [18.21],

and materials are hardened due to the pile up of dislo-

cations [18.48, 49]. Grain boundary sliding also plays

an important role in mechanical behavior at elevated

temperatures [18.50]. Asaro and coworkers [18.51]pro-

posed a concise model for single crystals which relates

the crystal slip to the macroscopic strain. In this section

we discuss plastic material behavior from a microscopic

view based on the Asaro model, and relate the micro-

scopic deformation to continuum deformation at the

macroscopic level. Inﬁnitesimal deformation theory is

employed throughout here, and this enables us to reduce

the simulation load drastically. Detailed discussions on

ﬁnitely deforming crystals can be found in the original

and related articles.

Metallic materials have a certain regularity of

atomic conﬁguration, such as body-centered cubic

Part E 18.4

Continuum Constitutive Modeling 18.4 Crystal Plasticity 1027

a) Friction coefficient 0.1 b) Friction coefficient 0.2

c) High strain rate d) Low strain rate

0.470

0.365

0.260

0.155

0.050

σ (GPa)

0.998

0.750

0.500

0.250

Fig. 18.11a–d The effects of friction

and speed on the forging process. The

top ﬁgures demonstrate the effect of

friction on martensite transformation

under low deformation rate, while the

bottom ﬁgure shows the equivalent

stress levels under different punch

speeds

(bcc), face-centered cubic (fcc), hexagonal close packed

(hcp), and so on. Each crystal structure has a particu-

lar plane and direction of permanent deformation. For

example, an fcc crystal has 12 primary slip systems.

Once we obtain a suitable model for describing the lo-

cal slip due to the local stress acting on a crystal, we

can then expect to be able to predict macroscopic defor-

mation as the sum of all local deformations. When slip

occurs in a crystal, the change of conﬁguration can be

expressed by the geometrical information of the system

that has undergone slip and the amount of slip γ .Fig-

ure 18.12 illustrates the basic idea of crystal slip. Let

(α)

be the plane and s

(α)

be the direction associated

with the slip system (α). Taking into account the dis-

tortion of the crystal lattice due to elasticity, the total

deformation gradient F (F

) can be expressed as

= F

∗

. (18.60)

Here F

∗

indicates the distortion and translation that are

mainly due to elastic deformation, while F

is the per-

manent deformation due to crystal slip. The velocity

F = F

(α)

Fig. 18.12 Schematic view of a slip system and the decomposition

of deformation

Part E 18.4