Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing

Подождите немного. Документ загружается.

988 Part E Modeling and Simulation Methods

17.2 Diffusionless Transformation

In MD simulations, we can only handle short-time phe-

nomena of the order of nanoseconds. Therefore, it is

difﬁcult to simulate processes or transformations that

rely upon long-range diffusion of atoms. In this sec-

tion, as examples of diffusionless transformations, we

shall pick the martensitic transformation and solid-state

amorphization, and investigate the microscopic mech-

anism underlying these transformations by using the

MD simulation.

17.2.1 Martensitic Transformation

The martensitic transformation, which is a typical dif-

fusionless transformations, will be studied from an

atomistic point of view using MD simulation in this sec-

tion. The martensitic transformation of ordered alloys

as well as that from fcc iron into a body-centered cu-

bic (bcc) structure will be investigated. The difference

between the martensitic transformation in nanoclusters

and the bulk will be also discussed.

For a typical system in which a martensitic transfor-

mation takes place, we consider here a 1 :1 alloy system

where the higher-temperature phase is the B2 phase,

like the Au-Cd or Ti-Ni system. In most alloy systems

where the B2 phase is found as a stable phase, the

atomic size difference would play an important role in

making the B2 structure stable. Therefore, for a simple

model for binary alloys, the interaction between atoms

is assumed to be described by the 8–4 Lennard-Jones

potential φ

(r) =e

⎡

⎣





−2





⎤

⎦

. (17.63)

Here the set of parameters e

and r

are deter-

mined [17.21] to reproduce the experimental data on

molar volumes, cohesive energy and heat of formation

of Ti, Ni and B2 phase of the Ti-Ni alloy.

The ﬁtted values of the parameters used in the

present simulation are listed in Table 17.1, where atom 1

Table 17.1 Parameters for the LJ potential in (17.63)

1.0000

0.8494

0.8947

1.13375

1.03387

1.24900

corresponds to the Ti atom and atom 2 to Ni; the length

scale is expressed in units of the diameter of atom 1,

while the energy scale is expressed in 0.5eV.Asacut-

off, a terminating process using third-order polynomial

functions, which starts at the inﬂection point of the 8–

4 LJ potential function (17.63), is taken, as discussed

in Sect. 17.1.4. For simplicity, we suppose that atoms 1

and 2 have the same atomic mass m. Throughout this

section, all units are normalized by the atomic mass m,

the diameter r

of atom 1, and the energy unit 0.5eV

in Table 17.1.

For an MD simulation in the NPT ensemble of this

binary system, we adopt the momentum-scaling method

for temperature control and the Parrinello–Rahman

method for pressure control. The period N

rescale

of the

momentum scaling is taken to be 10. The bookkeeping

radius r

book

is set at r

+0.6 and the period N

book

for

updating the book ranges from 25 to 100 according to

the temperature. The time integration is performed by

the ﬁfth Gear algorithm with a time step of Δt = 0.005

in the normalized units.

As an initial conﬁguration, a 16 × 16 × 16 B2 lat-

tice with an equilibrium lattice parameter a =0.9365

is prepared; snapshots are illustrated in Fig. 17.10.

The same number N/2 = 4096 atoms of elements 1

and 2 are arranged on the lattice points alterna-

tively, and small velocities randomly taken from the

Boltzmann distribution at a temperature T =0.001

(≈5.5 K) are assigned to all atoms. After annealing

at T =0.001 for 10

time integration steps, the sys-

tem remains in the B2 structure. This means that the

B2 structure is at least a metastable phase at low

temperature.

a) b)

Fig. 17.10a,b Snapshots of a B2 structure: (a) a perspec-

tive view and

(b) a top view from the z-direction. The light

gray spheres and the dark gray spheres denote the elements

1 and 2, respectively

Part E 17.2

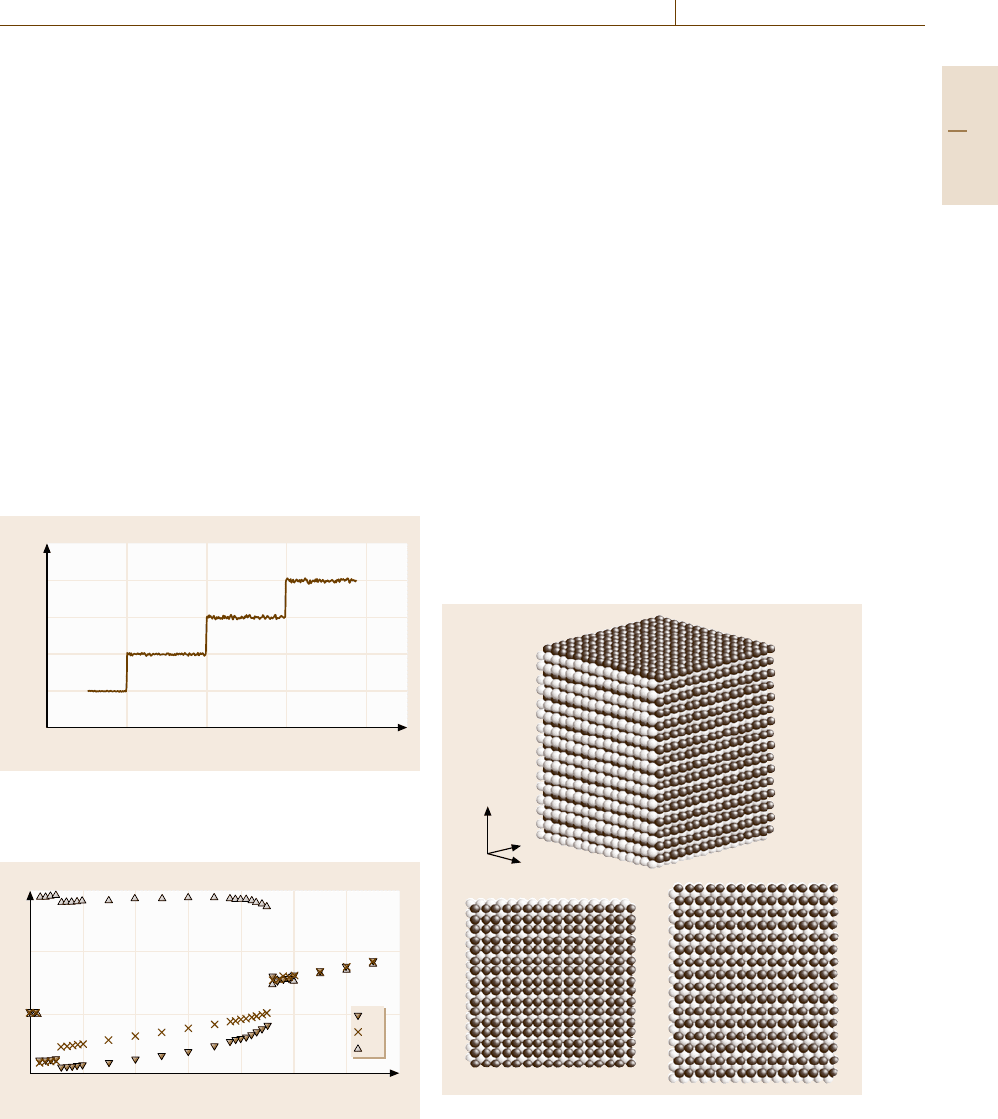
Molecular Dynamics 17.2 Diffusionless Transformation 989

After the annealing process at T =0.001, a heat-

ing procedure is performed in a stepwise way, as

shown in Fig. 17.11. The size of each heating step is

0.01(= 0.005 eV/atom ≈55 K) and every step is fol-

lowed by a 10 000 integration step equilibration period.

The physical values, such as the atomic volume and

energy, are determined by averages over the last 1000

steps of the equilibration period. To minimize the arti-

ﬁcial effect induced by the momentum-scaling process,

we execute the scaling procedure only if the effective

temperature (17.17) of the system deviates from the de-

sired value by more than 2%. Consequently, the scaling

procedures are concentrated in the ﬁrst 1000 steps of the

equilibration period.

Here one point should be noted about the rate of

temperature change in an MD simulation. In the step-

wise heating shown in Fig. 17.11, the average heating

rate is 2.0×10

−4

in the normalized units. This corre-

sponds to an extraordinarily high rate, around 10

K/s,

0.04

0.03

0.02

0.01

20000 30000 40000 50000

Time steps

Fig. 17.11 A snapshot of the time evolution of the system

temperature T calculated from the total kinetic energy of

atoms in a stepwise heating procedure

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

Cell axis length

Temperature

Fig. 17.12 The temperature dependence of the axis length

of the simulation cell in the heating process starting from

a B2 structure

although this rate is so low that it takes a considerable

calculation time of the order of hours. We shall en-

counter this type of discrepancy between the time scale

in the simulation and the actual calculation time in every

stage of MD simulations.

To take the statistical and thermal nature into ac-

count, several heating runs are carried out from different

initial perturbations. Before the crystal starts to melt, the

crystal structure experiences some structural transfor-

mations. By monitoring the shape of the periodic simu-

lation cell, we can see how the transformation evolves.

The time evolution of the shape of the simulation

cell in the heating procedure starting from a B2 phase

is shown in Fig. 17.12, where the cell axis lengths are

shown as functions on the temperature. The B2 phase

immediately transforms into a tetragonal phase with

a symmetry L

= L

= L

at T =0.02, and then trans-

forms into an orthorhombic phase with L

= L

at T =0.06. We call the former phase L1



and the latter

phase L1



, because both phases are understood as slight

modiﬁcations of an fcc-based close-packed structure

with a long-period modulation. Snapshots of the



phase and the L1



phase are shown in Figs. 17.13

b) c)

Fig. 17.13a–c Snapshots of an L1



structure: (a) perspec-

tive view,

(b) a top view from the z-direction, and (c) a side

view from the x-direction. The atoms are shown using the

same colors as in Fig. 17.10

Part E 17.2

990 Part E Modeling and Simulation Methods

a) b) c) d)

Fig. 17.14a–d Snapshots of an L1



structure: (a) a perspective view, (b) a top view from the z-direction, (c) a side view

from the x-direction, and (d) a side view from the y-direction. The atoms are shown using the same colors as in Fig. 17.10

and 17.14, respectively. Upon further heating, the sys-

tem transforms back into the B2 phase at T = 0.46,

and ﬁnally, the B2 crystal melts into the liquid phase

at T =0.66.

To understand the phase evolution in the heating

process shown above, we shall estimate the enthalpy

of each phase found in the simulation. Once we know

the atomic conﬁguration of the phase, we can calculate

the enthalpy at 0 K of each structure using an energy-

minimization process, which is equivalent to an MD

calculation at 0 K, if the corresponding structure has

a marginal stability at 0 K. The calculated energy lev-

els at 0 K for the B2, the L1



,andtheL1



phase are

shown in Fig. 17.15. This suggests that the L1



phase is

the ground state and the B2 phase is a fragile metastable

state at 0 K. Therefore, the B2-to-L1



transition at T =

0.02 is considered to be a simple transition from an un-

stable state to the ground state, while the L1



-to-L1



transition at T = 0.06 and the L1



-to-B2 transition at

T = 0.46 are understood as the phase transitions to the

–10

–10.1

Energy

B2 –10.000

B190

–10.026

–10.077

–10.079

Fig. 17.15 Energy

levels of

(meta-)stable

structures found

at 0 K

higher enthalpy states driven by the entropy contribu-

tion to the free energies.

The character of the transition between the B2

and the L1



phase can be seen from the tem-

perature dependence of the potential energy. If we

stop the heating process at a temperature between

T = 0.46 and 0.65 before melting and cool down

the system, we can observe the transition from the

B2 phase to the L1



phase. Figure 17.16 shows

the change of the potential energy per atom in

a heating process (triangles) and a cooling process

(circles) at a rate of 2.0×10

−4

. We can see a hys-

teresis behavior, which means that there is some

extent of superheating (supercooling) in the heating

(cooling) process with such a high heating (cooling)

rate.

For traditional reasons, the transition tempera-

ture M

of a martensitic transformation is deﬁned by the

transition from the high-temperature phase into the low-

temperature phase, and the transition temperature from

the low-temperature phase into the high-temperature

phase is called the reverse transformation tempera-

ture A

. Following this convention, Fig. 17.16 tells

us that the martensitic temperature M

of the B2-to-



transformation is 0.39 and the reverse martensitic

temperature A

of the L1



-to-B2 transformation tem-

perature is 0.46 at this cooling/heating rate. It also

suggests that the equilibrium temperature T

between

the L1



phase and the B2 phase should be around 0.43.

It should also be noted that the potential energy jumps

up at the L1



-to-B2 transition, which means that this is

certainly an entropy-driven transformation.

In general, it is likely that the higher-temperature

phase has a structure with higher symmetry. In this

Part E 17.2

Molecular Dynamics 17.2 Diffusionless Transformation 991

–9

–9.2

–9.4

0.35 0.4 0.45 0.5

Internal energy

Temperature

B2 phase

Heating

Cooling

0 phase

Fig. 17.16 Change of the potential energy per atom with

temperature in a heating and a cooling process

context, it is natural that the highest-temperature phase

B2 has a cubic symmetry, L

= L

.However,it

is somewhat strange that the lowest-temperature phase



has a tetragonal symmetry L

= L

= L

, while

the middle-temperature phase L1



only has orthogo-

nal symmetry L

= L

. This can be understood

if we look into the translational symmetry. As shown

in Figs. 17.13 and 17.14, the lower-temperature phases



and L1



show a breakdown of translational sym-

metry due to the presence of a periodic modulation of

the position of atoms, which makes the translational pe-

riod of the corresponding direction twice as long as that

of the B2 phase. For the L1



phase, this type of break-

down of translational symmetry is found in the x-and

z-directions, while it is found in all three directions for

the L1



phase. Therefore, in this sense, the translational

symmetry reduces step by step from the B2 phase to the



phase.

Although the LJ potential parameters used here are

determined by the static properties of the Ti-Ni system,

the structure of low-temperature phases





and L1





found in the simulation is different from that experi-

mentally observed in the system, which is a hexagonal

phase called B19



. We have also calculated the energy of

hexagonal based structure starting from the B19 struc-

ture, and found a metastable structure that is a sort of

modulation of B19, tentatively called B19



.However,

the energy of the B19



phase is higher than those of L1



and L1



, although it is lower than that of B2, as shown

schematically in Fig. 17.15.

In spite of these drawbacks of this LJ potential, this

model system has interesting features found in many

martensitic transformations, that is, the existence of the

martensites with long-period modulation, a series of

martensites at low temperatures, and the hysteresis be-

havior in the upward/downward transformation. It is

quite amazing that such a simple two-body potential can

reproduce a variety of aspects common to martensitic

transformations. Therefore, in the next section, we shall

use this model to investigate how the transformation

properties would change in nanoclusters.

17.2.2 Transformations in Nanoclusters

Some physical properties become different from those

in the bulk in nanosized clusters. In this section, we

shall investigate how the phase-transformation behav-

ior changes in such nanoclusters by performing the MD

simulation for the model for B2 alloy clusters and iron

clusters with a special focus on the martensitic transfor-

mation.

In general, physical properties change in small clus-

ters. For example, the melting temperature goes down

in nanosized clusters of pure metals [17.22]. Even the

stable phases change dramatically in nanoclusters of al-

loys [17.23]. On the other hand, due to the ﬁniteness of

the total number of atoms in the system, nanoclusters

are appropriate targets for MD simulation. Therefore,

we shall investigate how the transformation properties

would change for nanoclusters by using the simple

model of martensitic transformation discussed in the

previous section as well as a pure-iron system described

by a simple EAM potential.

Transformation in B2 Alloy Clusters

A spherical nanocluster specimen with a B2 structure

is prepared at a temperature around A

for the bulk sys-

tem, as depicted in Fig. 17.17a. The temperature-control

method and the bookkeeping method are the same as in

the bulk case discussed in the preceding section, while

there is no need for boundary conditions for a free sin-

a) b)

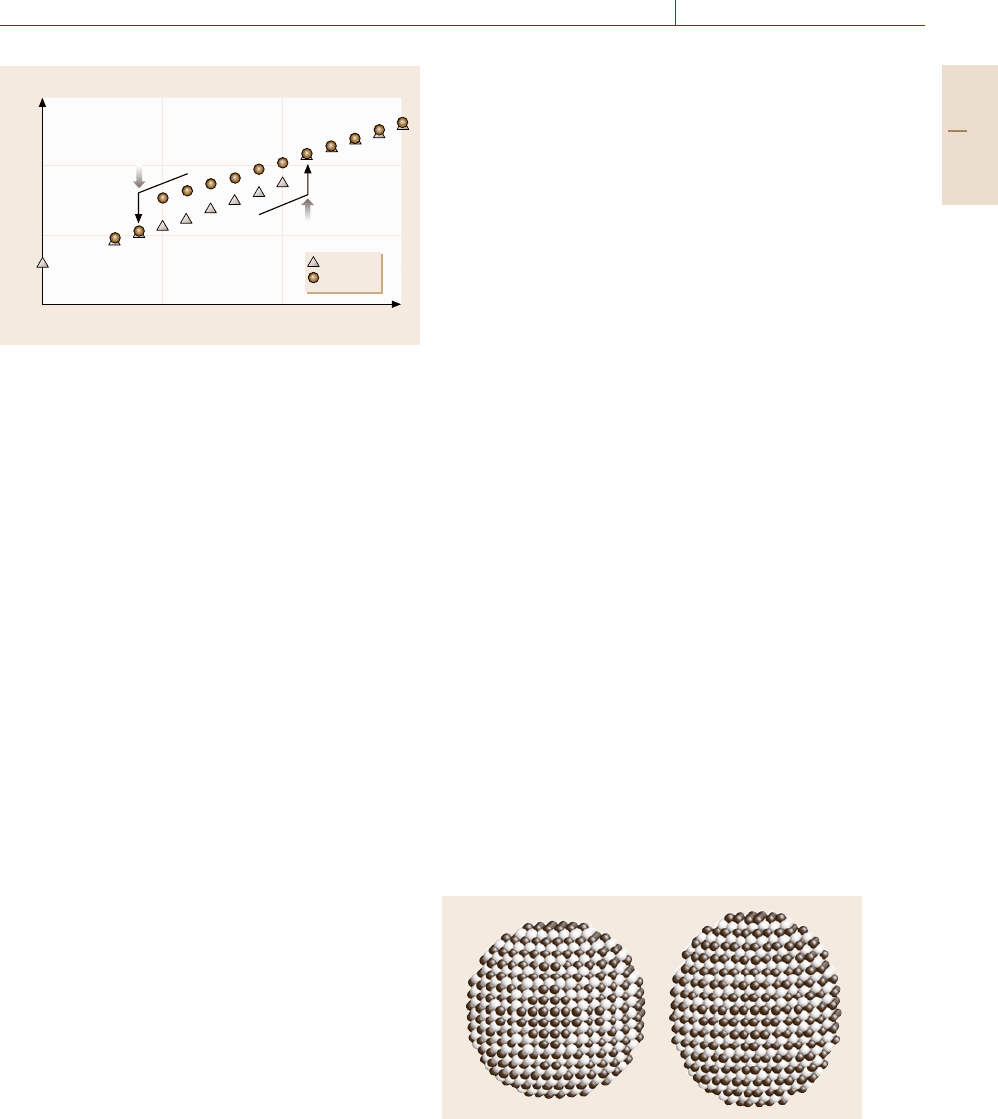
Fig. 17.17a,b Snapshots of nanoclusters with N = 4279

atoms: (a) a B2 cluster and (b) an L1



cluster. The atoms

are shown using the same colors as in Fig. 17.10

Part E 17.2

992 Part E Modeling and Simulation Methods

gle cluster, or equivalently, a ﬁxed boundary condition

is imposed. By lowering the temperature, we can ob-

serve a martensitic transformation into the L1



structure

as we found in the bulk case with periodic bound-

ary conditions. A snapshot of the L1



cluster of the

low-temperature phase is also depicted in Fig. 17.17b).

When we observe a martensite at low temperatures, we

raise the temperature to observe a reverse transforma-

tion as well as melting of the cluster. By performing

such simulation processes for the various sizes of nano-

clusters, we can detect [17.24] the dependencies of the

martensitic transformation temperature M

, the reverse

transformation temperature A

, and the melting temper-

ature T

on the cluster size.

The calculated cluster-size dependencies of the

transformation temperatures M

(closed triangles), A

(open triangles), and the melting temperature T

(closed circles) are shown in Fig. 17.18, where the tem-

perature is expressed in the same units as in Fig. 17.16.

Throughout the simulations the cooling and the heat-

ing rate is 2.0×10

−4

. All transformation temperatures

decrease on decreasing the cluster size. In particular,

the dependence of both A

and M

on the cluster size

shows good agreement with the experimental data on

Au-Cd alloy nanoclusters [17.25]. These results indi-

cate that the decrease of the martensitic temperature is

caused not by the increase of the activation barrier of the

0 5000 10 000

Number of atoms

Temperature

0.2

0.4

0.6

Bulk

Fig. 17.18 The size dependence of the melting temperature

and the martensitic temperatures M

and A

of the B2

nanoclusters, together with those for the bulk B2 phase on

the right edge of the graph

transformation, but by the decrease of the equilibrium

temperature T

between the B2 phase and the marten-

site in this model. Moreover, since both the martensitic

transformation and the melting are entropy-driven trans-

formations, these results also suggest that the origin

of the peculiar transformation behavior of nanoclusters

should be mainly due to the fact that the thermal vibra-

tional state of atoms changes in nanoclusters due to the

drastic increase of the population of atoms belonging to

the free surface.

Transformations in Iron Clusters

As pointed out above, the transformation properties

of nanoclusters are closely related to the existence of

a large portion of surface atoms in nanoclusters. In this

context, we shall investigate the effect of the surface by

using another model for iron clusters.

For an iron potential, we use a simple EAM po-

tential developed by Johnson and Oh [17.26]. In their

model, the electron-density function f (r)andthetwo-

body potential ϕ(r) have the following forms

(r) = f





−β

, (17.64)

(r) =



i=0



r/r

−1



, (17.65)

together with terminating procedures using third-order

polynomials starting at r

= 1.20253r

and vanishing

at r

= 1.39385r

for both functions f (r)andϕ(r).

To include the strong core–core repulsion in the two-

body term, Johnson and Oh introduced the stiffening

modiﬁcation

(r) =ϕ

(r) +k



(r) −ϕ





r/r

−1



(17.66)

which is valid for r < r

The embedding function F(ρ) has the analytic form

F(ρ) = F

[1 −ln(ρ/ρ

)

](ρ/ρ

)

(17.67)

where ρ

is the equilibrium electron density of the bcc

phase with equilibrium lattice parameter 2/

√

,and

and n are ﬁtting parameters.

Table 17.2 Parameters for the EAM potential (17.64–

17.67)

(Å) 2.4824 φ

(eV) −0.2651

(Å

−3

) 1.0000 φ

(eV) −0.8791

β 6.0000 φ

(eV) 9.2102

(eV) −2.5400 φ

(eV) −13.3088

n 0.3681 k

12.0630

Part E 17.2

Molecular Dynamics 17.2 Diffusionless Transformation 993

The potential parameters found in (17.64–17.67) are

listed in Table 17.2, and are determined [17.26]bythe

available experimental data of the atomic volume, the

cohesive energy, the bulk modulus, the Voigt average

shear modulus, the anisotropy ratio, and the unrelaxed

vacancy-formation energy for bcc iron.

Due to the lack of explicit magnetic contribution to

the potential energy in this simple scheme, this potential

cannot reproduce the phase stability between fcc iron

and bcc iron at a given temperature. Instead, this poten-

tial stabilizes the bcc structure at any temperature for

thebulkaswellasclusters[17.27]. Therefore, if we

start the simulation from a metastable fcc phase, we

can observe the fcc-to-bcc martensitic transformation

if there is enough thermal excitation to overcome the

activation barrier from the fcc-to-bcc structure, but the

opposite transformation cannot be observed. However,

we can investigate an atomistic mechanism at the begin-

ning stage of the fcc-to-bcc martensitic transformation

by using this model.

In this case, we ﬁrst prepare fcc clusters with var-

ious sizes ranging from N = 400 to 10 000 atoms at

very low temperatures (≈10 K). The system tempera-

ture is controlled by the momentum-scaling method.

After a annealing and relaxing period of 10 000 time

steps with Δt = 0.005 ps, all clusters retain their initial

fcc structure, independent of their size. This means that

there is some potential barrier in the transformation path

between the fcc phase and the bcc phase for nanoclus-

ters. Then the clusters are heated up to melt at a heating

rate of around 5 K/ps.

In the heating process, an fcc-to-bcc transition is ob-

served [17.27] for the clusters with N < 8000 and the

transformation temperature increases as the cluster size

increases, while no explicit phase transformation is ob-

served before melting in the larger clusters. In contrast

Fig. 17.19 Snapshots of a transformation procedure of a Fe nano-cluster from fcc to bcc. The Bain transformation starts

from the upper-right surface and proceeds into the lower-left, in which the (100) plane of fcc changes into the (110) plane

of bcc

to the previous case for the B2 alloy clusters, these re-

sults suggests that the cluster-size dependence of the

fcc-to-bcc martensitic transformation temperature orig-

inates from the change in the height of the activation

barrier.

In this sense, the activation barrier is expected to

have a close relation to the surface structures of the

nanoclusters. Hence the initial stage of the fcc-to-bcc

transformation is analyzed with special attention to the

motion of surface atoms. As shown in Fig. 17.19,the

transformation starts from the surface of the nanocluster

and proceeds into the interior of the cluster. By ana-

lyzing the atomic correspondence between the initial

conﬁguration of an fcc cluster and the ﬁnal conﬁgura-

tion of a bcc cluster, a uniaxial transformation called the

Bain transformation takes place in this case. Moreover,

further simulation study reveals [17.27]thatavortex-

like collective motion is activated on the surface of

the clusters according to the temperature, and the col-

lision between two collective modes induces atomic

collective motion similar to the Bain transformation,

and stimulates the creation of an embryonic martensitic

transformation on the surface.

17.2.3 Solid-State Amorphization

Under extreme conditions, such as severe plastic de-

formations or irradiation damage, some alloy systems

show a crystal-to-amorphous transition. This solid-state

amorphization is considered as a sort of diffusionless

transformation. The physics behind the mechanism of

the solid-state amorphization will be investigated by

MD simulation for a model system in this section.

It is well known that the atomic size ratio between

the constituent elements plays an important role in the

amorphous formation of alloys [17.28]. Therefore, to

Part E 17.2

994 Part E Modeling and Simulation Methods

investigate the mechanism of solid-state amorphization,

we shall examine a binary system where the interaction

is described by the 8–4 LJ potential (17.63) as a model

for binary alloys, since we can easily vary the atomic

size ratio by changing the parameter r

Here we deal with the binary system composed of

elements 1 and 2, and, without loss of generality, as-

sume r

=1andr

≤1. The atomic distance between

different elements is deﬁned as r





/2.

To focus on the atomic size effect, we make a fur-

ther simpliﬁcation that all chemical bonding parameters

are identical, that is, e

= e

= 1. The atomic

masses of both elements are also supposed to be the

same unit mass. Consequently, the binary system is

characterized by only two variable parameters: the

atomic size ratio r

of element 2 to element 1, and the

concentration x

of element 2. All physical quantities

are expressed in the above units in this section.

The crystal-to-amorphous transformation processes

are simulated in the following procedures. We ﬁrst pre-

pare an fcc solid solution at nearly zero temperature

by randomly assigning the solute atoms to the fcc lat-

tice sites. After an annealing and relaxation period, we

then slowly heat up the system at a rate of 2.0×10

−4

In a system that has high glass-forming ability for al-

loys, the stability of the solid-solution phase against the

amorphous phase would be lost, and solid-state amor-

phization, that is, the transition from the solid solution

to an amorphous phase, should be observed if the sys-

tem acquires enough thermal excitation to overcome an

activation barrier.

MD calculations for a 4000-atom system with peri-

odic boundary conditions have been performed [17.29].

The pressure of the system is kept to zero by using the

a) b) c) d)

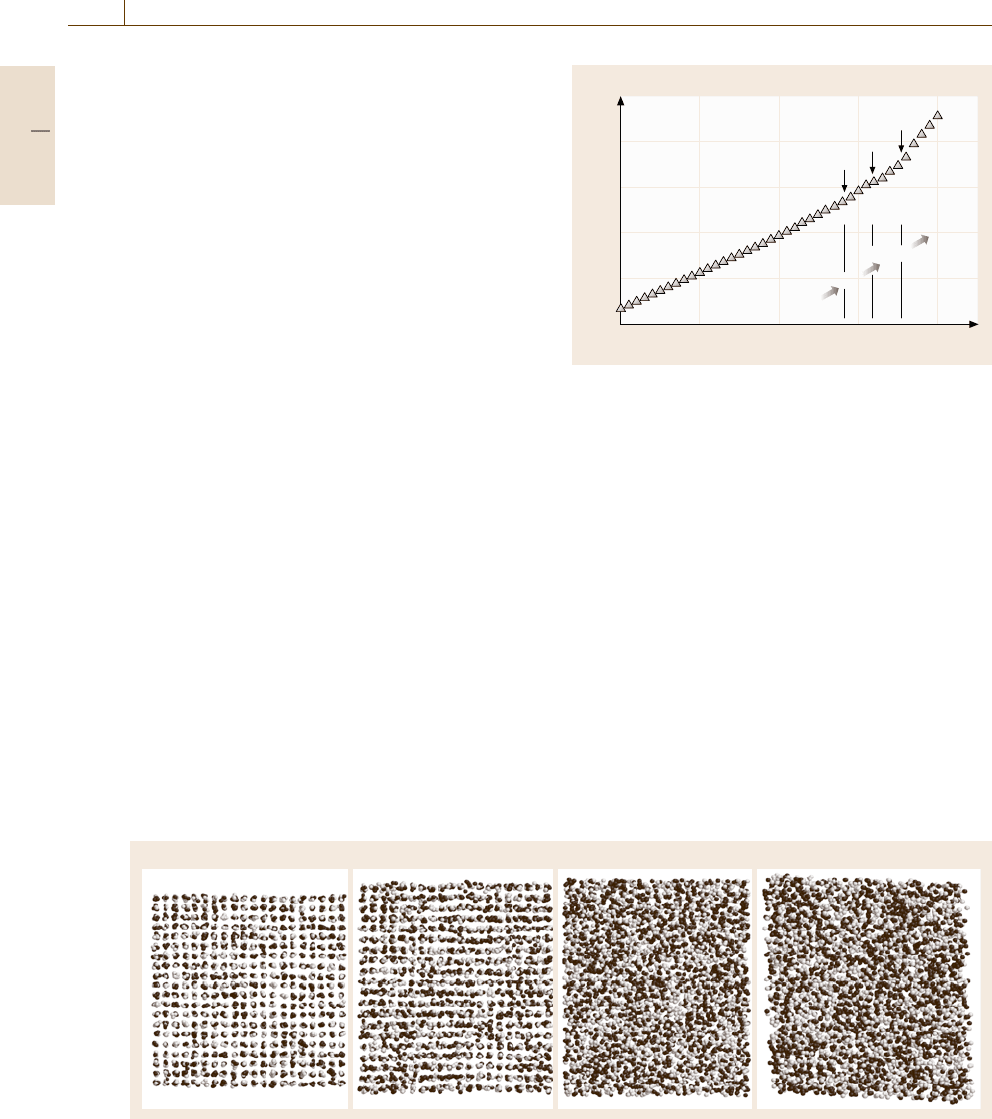
Fig. 17.21a–d Snapshots of the phases appearing in the heating process shown in Fig. 17.20: (a) an fcc solid solution (fct)

phase (T = 0.25), (b) a bcc solid solution phase (bct) phase (T = 0.29), (c) a glassy phase (T = 0.33), (d) a liquid phase

(T = 0.39). The light gray spheres and the dark gray spheres denote the elements 1 and 2, respectively

–7.2

–7.4

–7.6

–7.8

–8

–8.2

0 0.1 0.2 0.3 0.4

Energy

Temperature

Liquid

Glass

bcc

fcc

Fig. 17.20 Potential energy dependence on the tempera-

ture in a heating process from the fcc solid solution of the

2, x

) =(0.82, 0.50) system

Parrinello–Rahman method. The temperature of the sys-

tem is set to the desired value by the momentum-scaling

method. Figure 17.20 shows the potential energy evo-

lution in a heating process from an fcc solid solution

of the system where the atomic size ratio r

is 0.82

and the composition x

of the smaller elements 2 is

0.50. The fcc solid solution (or strictly speaking, face-

centered tetragonal or fct phase) ﬁrst evolves into bcc

solid solution (body-centered tetragonal or bct phase)

at T

= 0.28, and then into an amorphous phase at

=0.32, and ﬁnally into the liquid phase at T

=0.35.

The snapshots of each phase found in this heating

process are shown in Fig. 17.21, where the light gray

spheres and the dark gray spheres denote the elements 1

and 2, respectively. Note that there is only a small jump

in the potential energy at the phase transition at T

and

Part E 17.2

Molecular Dynamics 17.3 Rapid Solidiﬁcation 995

a) b) c) d)

Fig. 17.22a–d Snapshots of atomic conﬁguration of the prepared samples arranged on the fcc lattice sites and annealed at

T =0.001 in several systems with different atomic size ratio r

: (a) the (r

, x

) =(0.82, 0.50) system, (b) the (r

, x

) =

(0.81, 0.50) system, (c) the (r

, x

) =(0.80, 0.50) system, and (d) the (r

, x

) =(0.79, 0.50) system. The colors of the

atoms are the same as in Fig. 17.21

, while drastic structural changes are found between

the different phases, as shown in Fig. 17.21.

Similar calculations were performed while varying

the atomic size ratio r

at x

=0.25, 0.50, and 0.75. At

each concentration, we observe the transition from solid

solutions to amorphous phases if r

is less than some

corresponding critical ratio r

, while no amorphiza-

tion but melting accompanying with a potential energy

jump is observed if r

is larger than r

. Especially,

if r

is considerably below r

, we ﬁnd a solid-state

amorphization in the preparation stage of the initial fcc

conﬁguration at nearly zero temperature, as shown in

Fig. 17.22 for the x

=0.50 case.

Thus, for a given atomic size ratio, we can roughly

estimate the composition range where the solid-state

amorphization would be observed in the heating and

annealing processes in the simulation. The results are

shown by the shaded region in Fig. 17.23. This sug-

gests that a large atomic size ratio produces a high

glass-forming ability into the binary alloy systems. The

same tendency in the glass-forming ability for a bi-

nary system was reported in a similar MD study using

1.00

0.90

0.80

0.70

0.60

0 0.25 0.5 0.75 1

Atomic size ratio

Concentration

Melting

Solid-state

amorphization

Fig. 17.23 The atomic size dependence of the composition

range in which solid-state amorphization is observed

the 12–6 LJ potential [17.30]. We also note that the

effect of the atomic size ratio on the glass-forming

ability has a slightly asymmetric nature, that is, the

glass-forming tendency is higher at x

=0.75 than at

=0.25 (x

=0.75). This feature can be found in the

atomic size effect on the glass-forming ability under

rapid solidiﬁcation, which is one of the topics to be

discussed in the next section.

17.3 Rapid Solidiﬁcation

The rapid solidiﬁcation procedure is also a short-time

process that can be handled by MD simulation. In

this area, there are a lot of interesting topics, such

as the physics of glass transition, the local structure

and vibrational state of glassy materials, the prepara-

tion of amorphous alloys, and nanocrystallization found

in the annealing process of amorphous phases. In this

section, we shall tackle these problems in the MD

framework.

17.3.1 Glass-Formation by Liquid Quenching

In this section, rapid solidiﬁcation processes from the

melt are simulated for Ti-Al binary alloy systems. The

glass-forming condition is discussed in relation to the

experimental observations.

One of the most popular preparation methods of

amorphous alloys is the rapid solidiﬁcation process

from the melt. In ordinary rapid solidiﬁcation processes,

Part E 17.3

996 Part E Modeling and Simulation Methods

the cooling rate is in the range 1–10

K/s, which is hard

to handle by MD simulation. However, the Ti-Al bi-

nary system has such poor glass-forming ability that the

amorphous phase can be obtained only by sputtering de-

position [17.31]. The effective cooling rate in vapor de-

position experiments might reach the order of 10

K/s

or more, which is tractable even in MD simulations. In

this sense, the Ti-Al system is adequate for MD studies

on amorphous formation and its crystallization.

In addition, Ti-Al alloys have both technical and

theoretical interest, because their excellent mechanical

properties strongly depend on their composition and the

microstructure. The microstructure can be controlled by

heat treatment through a metastable state such as the

amorphous phase. Hence it is important to understand

the microscopic mechanism involved in the formation

and crystallization of the amorphous phases.

We use an EAM potential for Ti and Al devel-

oped by Oh and Johnson [17.32]. In their scheme, the

electron-density function f (r) and the two-body poten-

tial ϕ(r) for the pure metal A are supposed to have the

exponential forms

(r) = f

exp



−β



r/r

−1



, (17.68)

(r) =ϕ

exp



−γ



r/r

−1



, (17.69)

where f

, ϕ

, β

and γ

are parameters, and r

is the equilibrium nearest-neighbor distance. The em-

bedding function F

(ρ) is determined by the Rose

function E

(r) according to the procedure discussed

in Sect. 17.1.4 by using the modiﬁed form of the Rose

function

(r) =−E



1 +α



r/r

−1

'

r/r



−m



r/r



−1

(

−α



r/r

−1



(17.70)

Table 17.3 Parameters of the EAM potential for the Ti-Al

system

TiTi

(Å) 2.9511 r

AlAl

(Å) 2.8635

(Å

−3

) 0.4 f

(Å

−3

) 1.0

6.0000 β

5.000

(eV) 0.51132 φ

(eV) 0.09539

8.9971 χ

11.5

(eV) 4.85 E

(eV) 3.58

4.743 α

4.594

2.4 m

2.37

and (17.49)and(17.50). The potential parameters found

in (17.68–17.70) are listed in Table 17.3; these are de-

termined [17.32] by the available experimental data of

the atomic volume, the cohesive energy, the bulk mod-

ulus, the Voigt average shear modulus, the anisotropy

ratio, and the unrelaxed vacancy formation energy for

fcc Al and hexagonal close-packed (hcp)Ti.

The Ti-Al cross potential is created by using

Johnson’s method [17.33], in which the cross potential

between the elements A and B can be written by us-

ing the functions from the pure A–A and the pure B–B

potential as

(r) =



(r)

(r) +

(r)



(17.71)

The only ﬁtting parameter in (17.71) is the ratio f

/ f

We have determined the ratio f

/ f

to reproduce the

experimental value of the heat of solution [17.34]. The

ﬁtted value is also listed in Table 17.3.

Here one point should be noted about the EAM

potential above. The potential is prescribed so as to re-

produce the static properties of hcp Ti and fcc Al such as

the cohesive energy, the lattice constant and the elastic

constants. But it cannot reproduce correctly the forma-

tion energy of the intermetallics in the Ti-Al system

such as Ti

Al, TiAl, and TiAl

Since we have a particular interest in the effect of

the difference of the potential used in the simulation

on the simulation results, the 8–4 LJ potential is also

used in another series of simulations. The parameters

used in the simulations are listed in Table 17.4,which

are ﬁtted [17.35] so as to reproduce a Ti-rich portion of

the phase boundaries in the Ti-Al system in the cluster

variation method (CVM) framework.

To perform the MD simulation of NPT ensembles,

we use the momentum-scaling method every 10 steps

and the Parrinello–Rahman method to keep the internal

pressure zero. The ﬂexible mobility of the simulation

Table 17.4 Parameters of the LJ potential for the Ti-Al sys-

tem

TiTi

(Å) 2.922

AlAl

(Å) 2.864

TiAl

(Å) 3.029

TiTi

(eV) 0.812

AlAl

(eV) 0.559

TiAl

(eV) 0.812

Part E 17.3

Molecular Dynamics 17.3 Rapid Solidiﬁcation 997

–4.5

–4.6

–4.7

–4.8

–4.9

0 200 400 600 800 1000 1200 1400 1600 1800

Amorphous

300 K

Crystal

300 K

Energy (eV)

Temperature (K)

1.0 K/ps

10K/ps

100 K/ps

Fig. 17.24 The temperature dependence of the internal energy of the Ti-25 at. % Al system in the cooling processes: the

squares,theopen triangles,andtheclosed triangles correspond to the case with the cooling rate of 1.0, 10, and 100 K/ps,

respectively. The left graphs are snapshots of atomic conﬁguration and the pair distribution functions of an amorphous

phase (upper) and a crystalline phase (lower) at 300 K

cell in the Parrinello–Rahman scheme has the advan-

tage of minimizing the restriction due to the periodic

boundary conditions, which is especially important in

crystallization processes. The equation of motion is nu-

merically integrated using the ﬁfth Gear algorithm with

a time integration step of 0.004 ps.

The MD simulation of the rapid solidiﬁcation pro-

cess in the Ti-Al systems of various compositions is

carried out in the following way. In the ﬁrst stage, to

make a liquid phase of Ti-Al alloys, we prepare an

fcc solid-solution as an initial conﬁguration in a simi-

lar manner discussed in Sect. 17.2.3. By annealing it at

a high temperature (≈2000 K) above the melting point,

the initial structure immediately melts. Since the atomic

diffusion rate is high in the liquid phases, an isothermal

annealing period of 2 × 10

steps (≈0.8 ns) is consid-

ered to be enough to acquire a sample of the equilibrium

liquid state at a given composition.

In the next stage, we choose a liquid phase obtained

by the aforementioned prescription as a starting con-

ﬁguration. Then we cool the system down to 10 K in

a stepwise manner with various rates ranging from 10

to 10

K/s. Whether we obtain a crystalline phase or

an amorphous phase at the end of the cooling process

depends on both the cooling rate and the composition.

If we have an amorphous phase, we then raise the tem-

perature of the system up to melting, or, if necessary,

keep it at some temperature for isothermal annealing.

In the course of the heating or annealing procedure,

a structural relaxation process in the amorphous phase

and, in some cases, a crystallization process from the

amorphous state could be observed.

Some typical evolutions of the internal energy dur-

ing cooling processes for the Ti-25 at. % Al system of

4096 atoms are shown in Fig. 17.24, where the squares,

the open triangles, and the closed triangles correspond

to the cooling rate with 1.0, 10, and 100 K/ps. The sud-

den drop of the internal energy at around T = 900 K

in the slowest cooling case corresponds to a liquid-to-

crystal transition. On the other hand, the discontinuity

in the slope in the two faster cooling cases corresponds

to a glass transition, using which we can deﬁne the

glass transition temperature T

, as denoted in Fig. 17.24.

The left graphs in Fig. 17.24 are snapshots of atomic

conﬁgurations of an amorphous phase (upper) and

a crystalline phase (lower) at 300 K together with the

pair distribution functions of the corresponding phase,

which reﬂects a typical feature in each phase, that is,

Part E 17.3