Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing

Подождите немного. Документ загружается.

978 Part E Modeling and Simulation Methods

–1

–2

–3

–4

–5

–6

–7

–8

–9

–10

–11

–12

–13

0.001 0.01 0.1

MD time step Δt

Deviation from exact solution

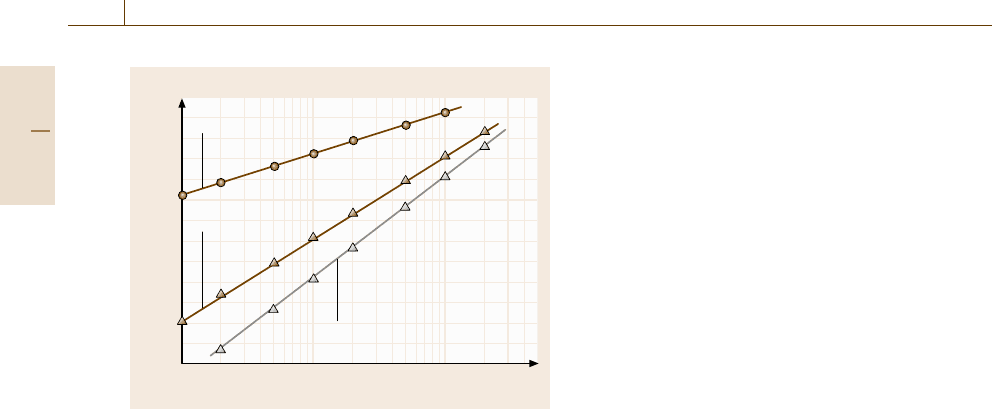
Verlet

k = 2.00

Gear

k = 3.99

Gear

k = 4.97

Fig. 17.2 The relation between the deviation in particle tra-

jectory from the exact solution of the harmonic oscillator

after 100 cycles and the calculation time step Δt.The

slope k of the linear approximation of each set of plots is

also depicted

the system considered. However, in the case of the

simulation of complex systems of many atoms, nu-

merical errors might also originate from other factors

such as an artiﬁcial cutoff of the interactions or com-

puter roundoff errors in the numerical treatment. So,

we cannot deﬁnitely conclude that the higher-order

Gear methods are superior to the Verlet method. In

some practical simulations of a small protein [17.3],

the Verlet method does show more accurate energy

conservation than the higher-order (fourth to eighth)

Gear methods for a considerably large time step, al-

though the calculation time is shorter and the consumed

memory space is lower for the Verlet methods. In

a practical sense, we should choose these numer-

ical methods depending on available computational

resources such as calculation speed and memory

storage.

Program Languages

and Computational Platforms

To end this section, we consider the program languages

in which the calculation code is written and the plat-

forms on which the MD calculations are performed.

The program that executes MD calculations on com-

puters are usually written in particular languages. The

FORTRAN language is one of the most popular due to

its historical use for supercomputers. Of course, other

program languages such as the C or JAVA are also good

for the coding MD programs.

In terms of the platform for the simulation, any

type of computer, for example supercomputers, work-

stations, personal computers (PCs), or others, can be

used for MD simulations. Any type of operating sys-

tem, such as UNIX, Windows, Macintosh, or Linux,

will work, as long as it supports the language used.

In particular, since the main part of the MD calcula-

tions consists of the computation of forces acting on

each particle, which can be calculated independently,

the use of computers with vector or parallel proces-

sors makes the calculation highly efﬁcient. In addition,

the computing power of modern personal computers

is sufﬁcient to perform MD simulations at a satisfac-

tory speed. Examples of typical calculation time of

MD simulations on a PC will appear in the following

section.

17.1.2 Constraints

on the Simulation Systems

MD simulation is inevitably restricted by computational

power. Therefore, in this section, we shall introduce two

remedies for this deﬁciency: periodic boundary condi-

tions and the bookkeeping method.

Since the typical time scale for atomic motions

is of the order of a picosecond (10

−12

) or less, we

should use values of the order of a femtosecond

(10

−15

) for the time step Δt to keep the numeric-

al errors small. Therefore, it takes many more than

a million iterations to follow the motion of a single

atom for just a microsecond. Moreover, the number

of calculations required grows rapidly as the num-

berofatomsN in the system increases. Under these

circumstances, we should satisfy ourselves with the

calculation of a small system with fewer than a mil-

lion atoms and a short physical process over less than

a few microseconds. Thus there is always a large dis-

crepancy in both length and time scale between the

real macroscopic system and the simulation system we

can handle. For example, the typical size of a million-

atom system is as small as a few tens of nanometers,

which means that the simulation system is far from

macroscopic.

Periodic Boundary Condition

A popular remedy for the length scale problem is the use

of periodic boundary conditions. As shown schemati-

cally in Fig. 17.3, we ﬁrst conﬁne all the atoms to a box,

and then copy the box, together with the atoms in the

box, identically in three directions. By repeating this

procedure, we can ﬁll the whole space with the original

Part E 17.1

Molecular Dynamics 17.1 Basic Idea of Molecular Dynamics 979

Fig. 17.3 An illustrative view of periodic boundary condi-

tions

conﬁguration and its replicas. Consequently, an atom

leaving the box to the right through one boundary can be

identiﬁed with an atom entering from the left at the op-

posite boundary. A system constructed in this way can

be taken as having inﬁnite size and an inﬁnite number

of atoms.

Of course the periodic system cannot be identical to

an inﬁnitely large bulk system. Some drawbacks caused

by periodic boundary conditions will be discussed in

later sections.

Bookkeeping Method

The main part of the calculational cost in solving

the equations of motion is due to the calculation of

the interactive forces between atoms, because, roughly

speaking, the number of combinations of interacting

atomic pairs grows as N

or faster with the total num-

ber of atoms N. If the atomic force has a long-range

interaction range, such as the Coulomb interaction,

this problem is very serious, and the complicated

Ewald method [17.4] is needed to perform calculations

effectively. On the other hand, if the interaction is short-

range, which is the case for most metallic systems,

a simple prescription called the bookkeeping method

effectively saves us a lot of calculation time.

The bookkeeping concept is simple: we keep

a book, in which a table of the neighboring atoms is

written down for all atoms in the system, and is reg-

ularly updated with a proper period ΔtN

book

.More

concretely, we ﬁrst calculate the members within a dis-

tance r

book

margin

of each atom, where r

is the

interaction range, and write them down in the book,

as illustrated schematically in Fig. 17.4. Then we need

only consider interactions between the atom and its

neighbors, as written in the book, in the following N

book

numerical integration steps. After every N

book

integra-

tion steps, we update the list of neighbors in the book

by calculating the distances between all atomic pairs.

The period N

book

for updating the book should be de-

termined according to N

book

vΔt =r

margin

, where v is

the average velocity of the atoms.

As previously mentioned, the calculation time re-

quired for the force calculation grows like N

a pairwise-interacting system, if we calculate the inter-

action for all pairs of atoms. On the other hand, when

we use the bookkeeping method, the time required only

grows linearly with N, because the average number of

atoms neighboring each particle is almost constant and

does not depend on N.

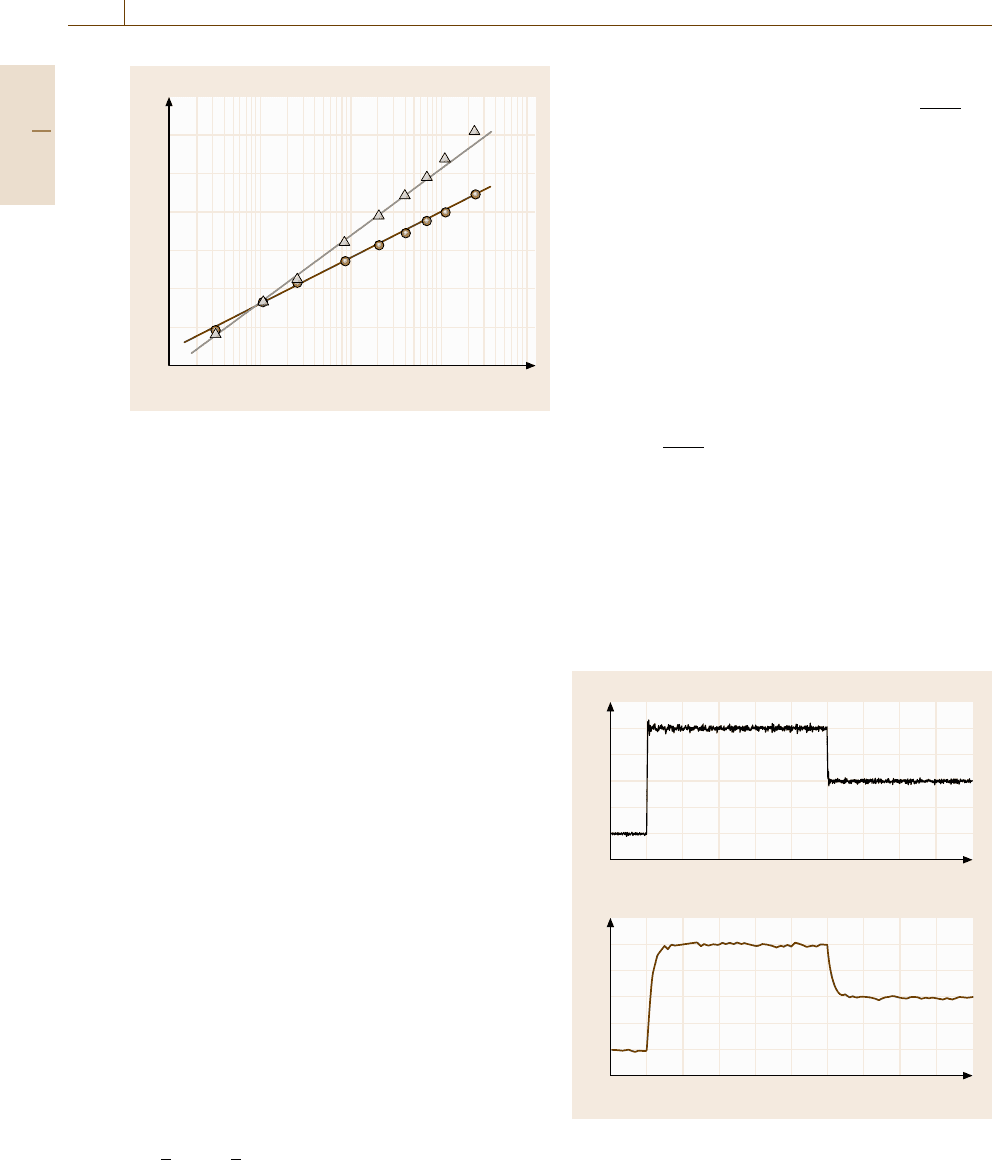
Figure 17.5 shows the relation between the cal-

culation time needed for 100 integration steps and

the total number of atoms N in a simulation cell.

In this calculation, we choose a system consisting of

pairwise-interacting atoms and use r

book

= 1.32r

and

book

= 50. The calculation program was coded in

the FORTRAN language and executed on a PC with

a single processor. In Fig. 17.5,wehaveshownthe

slope k of the linear approximation to each data set in

log–log plots. Note that the calculation time for the sim-

ulation with bookkeeping scales almost linearly, while

that of the simulation without bookkeeping scales al-

most quadratically, which leads to a d ifference of nearly

a thousand times in the calculation time for N = 20 000

atoms.

book

Fig. 17.4 An illustrative view of the regions related with

the bookkeeping method

Part E 17.1

980 Part E Modeling and Simulation Methods

–1

–2

–3

10 100 1000 10 000 100 000

Calculation time (s)

No bookkeeping

k = 1.85

Bookkeeping

k = 1.20

Fig. 17.5 The relation between the calculation time for 100

MD steps and the total number N of atoms in the simula-

tion system with and without bookkeeping

17.1.3 Control of Temperature and Pressure

To compare the simulation results with experimental

results, we must control the thermodynamical condi-

tions such as the temperature and the pressure of the

simulation system. The techniques for controlling the

temperature and the pressure of the simulation system

will be introduced in this section: the momentum-

scaling method and the Nose–Hoover thermostat for

temperature control, and the Andersen and Parrinello–

Rahman methods for pressure control.

Before introducing the control methods, we note

that the use of the control methods discussed below in-

cludes a subtle point; the standard way of temperature or

pressure control for the simulation system lies outside

the description of the Newtonian equations of motion.

Consequently, the deterministic nature of the MD simu-

lation will be lost and there is a risk that the simulation

results might depend on the control method we use.

Therefore, care should be taken when using such control

methods in MD simulations.

Momentum-Scaling Method

To control the temperature of the simulation system,

several methods have been presented. One of the sim-

plest methods is the momentum-scaling method [17.5,

6]. The temperature T of the system is deﬁned by the

average kinetic energy of all the atoms as

T =



, (17.17)

where k

is the Boltzmann constant. Accordingly, when

we want the system temperature to be T

, we rescale the

kinetic momenta of all atoms by a factor of

√

/T.

By executing this rescaling procedure repeatedly,

the system temperature will approach the desired

temperature. Even though this method appears too

naive and basic, it has been veriﬁed [17.7] that the

thermodynamical quantities will approach their equilib-

rium values after iterated equilibration processes using

momentum rescaling if the number of atoms N is sufﬁ-

ciently large.

One of advantages of this method is that the cod-

ing procedure is simple. For example, supposed that

the rescaling of the momenta is to be carried out

every N

rescale

steps, we would calculate the tempera-

ture T of the system according to (17.17), and insert

the momentum-scaling transformation for all atoms as

→



/T p

, (17.18)

after every N

rescale

integration steps.

In Fig. 17.6, we have depicted two examples of

the time evolution of the system temperature T in

a simulation in which the temperature is controlled

by the momentum-scaling method. Starting from an

equilibrated state at T =200 K, we have changed the

temperature to 400 K at t = 1000 steps, and then to

450

400

350

300

250

200

150

0 2000 4000 6000 8000 10 000

400

350

300

250

200

150

0 2000 4000 6000 8000 10 000

T (K)

MD steps

rescale

= 10

rescale

= 100

Fig. 17.6 Time evolution of the effective temperature T

of the simulation system calculated from the total kinetic

energy of the atoms

Part E 17.1

Molecular Dynamics 17.1 Basic Idea of Molecular Dynamics 981

300 K at t = 6000 steps. The upper graph shows the

case with N

rescale

=10, while the lower graph shows the

case with N

rescale

=100, where the convergence to the

desired temperature is slower. In both cases, the tem-

perature of the system is well controlled to the desired

value except for accompanying small ﬂuctuations.

Stochastic Method

There is another temperature-control method called the

stochastic method [17.8]. In this method, we pick an

atom at random and exchange its velocity with a value

taken at random from a Maxwell–Boltzmann distribu-

tion with the desired temperature T

. By executing this

prescription repeatedly every N

exch

steps, the system

should approach thermal equilibrium. However, it is dif-

ﬁcult to determine a proper value for the interval N

exch

An interval that is too short will generate a jiggling

behavior of atoms within a small conﬁguration space,

while an interval that is too long will result in a very

long calculation time to obtain the thermal equilibra-

tion at the desired temperature. In addition, there is

another shortcoming to the stochastic method, which

might bring about an unwanted steady state in the sim-

ulation system. Therefore, one should consult [17.9]if

using this method.

Nose–Hoover Thermostat

In contrast to the stochastic nature of the previous

method, there is a sophisticated temperature-control

method with a deterministic nature, called the Nose–

Hoover thermostat method [17.10, 11]. In this method,

a ﬁctitious variable S, which plays the role of a tem-

perature controller, is introduced into the mechanics of

the simulation system. The variable S serves as a sort

of friction of atoms, and its value depends on the differ-

ence between the system temperature T and the desired

temperature T

. The equations of motion of the ex-

tended system are the following

=−

∂φ

∂r

−

, (17.19)





−3Nk



, (17.20)

where Q is the ﬁctitious mass of the variable S. The

dotted symbols denote their time derivatives.

The role of the variable S can be seen more clearly

if we introduce a variable ς =

S/S and rewrite (17.19)

and (17.20)as

=−

∂φ

∂r

−ςv

, (17.21)

dς





−



. (17.22)

We can see that the second term on the right-hand

side of (17.21), which is proportional to atom velocities,

serves as a sort of friction term, whose value depends

on the difference between the system temperature T

and the desired temperature T

. It has also been ver-

iﬁed [17.7] that this extended system gives the same

partition function as that of the original system in the

thermal equilibrium limit.

If we consider the ﬁctitious variable S as the co-

ordinate of an additional atom, which has a peculiar

equation of motion (17.20), then a coding procedure can

be executed similarly. However, since (17.19–17.22)

contain velocity dependent terms, a simple leap-frog

method does not work straightforwardly. In this case,

use of a predictor–corrector method is appropriate. For

example, using the Gear method, the coding procedure

is the following: (Here we shall use one dimen-

sional expression x

(t) for the atom coordinates for

simplicity.)

Step 1 For the p-th order method, specify the initial po-

sition x

) and its derivatives x



), x



),...,

and x

(p−1)

) and assign them to q

)fori =1

to N.

Step 2 Consider S(t) as coordinates of the (N +1)-

th atom, specify the initial value for S(t

)and

its derivatives S



), S



),...,and S

(p−1)

and assign them to q

N+1

Step 3 Calculate the predicted coordinates

+Δt)

for i = 1toN +1 at the ﬁrst step according to

(17.11).

Step 4 Calculate the force F

+Δt) at the ﬁrst step

for i = 1toN according to (17.19) by using

+Δt).

Step 5 Calculate the force F

N+1

+Δt)attheﬁrst

step according to (17.20) by using

+Δt).

Step 6 Compute the corrected q(t

+Δt) according to

(17.12)fori = 1toN +1.

Step 7 Repeat steps 3 to 6 with t

→t

+Δt.

Here one point should be noted about the meth-

ods in which ﬁctitious variables are introduced, such as

the Nose–Hoover thermostat. Once the motion of the

ﬁctitious variables has settled down, the ﬁctitious vari-

able does not harm the simulation system. On the other

hand, for example, if we try to increase the system tem-

perature by a large amount, the value of the ﬁctitious

variable starts to change very rapidly, so the tempera-

ture of the system will rise to the target value. However,

Part E 17.1

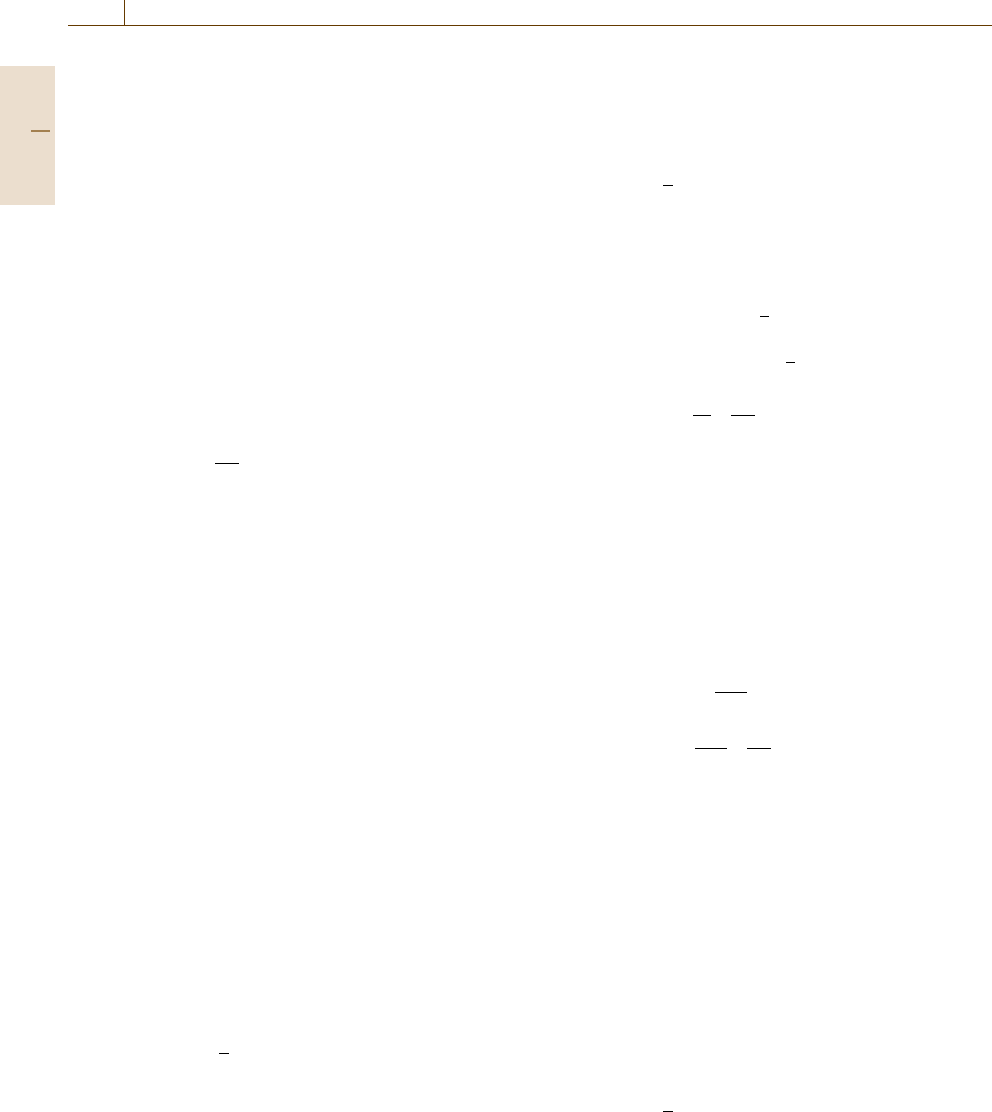
982 Part E Modeling and Simulation Methods

when the system temperature reaches the desired value,

the motion of the ﬁctitious variables goes on due to their

inertia, which results in the temperature continuing to

rise until the motion of the variable stops. This type of

overshooting behavior is an inevitably result of meth-

ods with ﬁctitious variables. We shall see an example of

such undesirable behavior in the case of pressure control

in the following.

Boundary Box Scaling

If the simulation system has a ﬁxed boundary, we cannot

control the pressure of the system. Therefore, pressure

control methods are always accompanied by changes of

the boundary conditions. Suppose that the simulation

system is contained in a boundary box of volume V,the

internal pressure of the system can be calculated using

the virial formula

int

αβ





iα

iβ

−q

iα

∂φ/∂q

iβ



, (17.23)

where the Greek symbols take the Cartesian values

1, 2, or 3. So a simple method is to enlarge the size of

the simulation cell if we want to decrease the pressure,

and vice versa. In more concrete words, if the bound-

ary box has a pallerelpiped shape spanned by the three

vectors (abc) =h, where h

αβ

is a 3 × 3 tensor, we can

control the pressure P

int

of the system by varying the

cell shape according to

αβ

→h

αβ



1−ε



0αβ

−P

int

αβ





, (17.24)

where P

is the desired pressure and ε is an appro-

priate small parameter. This method is similar to the

momentum-scaling method in some sense.

Andersen Method

As in the case of temperature control, there are some

more sophisticated methods for the pressure control in

which a ﬁctitious variable is introduced in order to con-

trol the system pressure. In this case, the simulation cell

itself is taken as a ﬁctitious dynamical variable just like

the Nose–Hoover thermostat S. The total Lagrangian L

is deﬁned as

L = L

cell

, (17.25)



−φ(r

, r

,...) , (17.26)

cell

= K

cell

−P

ext

V , (17.27)

where K

cell

is the kinetic term of the simulation cell,

which depends on the method, P

ext

is the external

stress, and V =det h is the cell volume.

Several forms of K

cell

have been proposed. In

Andersen’s scheme [17.8], the shape of the cell is

restricted to be cubic, that is, h

αβ

= V

1/3

αβ

. The dy-

namics are described by

cell

, (17.28)

where the dotted variables denote their time derivatives

and M is the effective mass of the cubic cell. In this

case, the equations of motion are the followings

/dt = p

−1

, (17.29)

/dt =−∂φ/∂r

−

−1

V p

, (17.30)

V/ dt







−r

·∂φ/∂r



−P

ext



, (17.31)

where the third equation means that the cell motion is

triggered by the deviation of the internal stress from the

external stress.

By introducing scaled coordinates s

parameterized

as r

= Ls

by the edge length L = V

1/3

of the cubic

cell, (17.29–17.31) can be rewritten as

/dt

=−

−1

∂φ/∂r

−2L

−1

, (17.32)

L/ dt

−2







)

−r

·∂φ/∂r



−P

ext



−2L

−1

. (17.33)

These expressions are more easy to handle for coding in

many cases.

Parrinello–Rahman Method

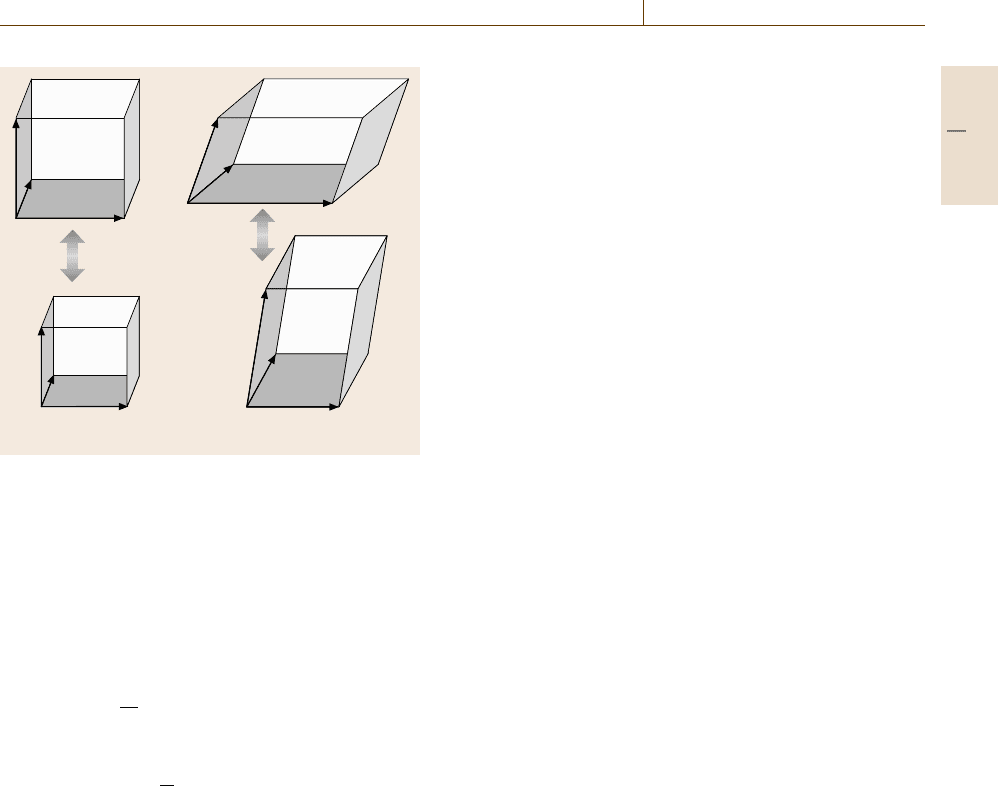
In the Parrinello–Rahman method [17.12], which is

a generalization of Andersen’s method, the shape of the

simulation cell is allowed to deform more ﬂexibly. The

periodic box has a pallerelpiped shape spanned by the

three vectors (abc) =h, as shown in Fig. 17.7. The

kinetic part is written as

cell

Mtr





(17.34)

where

h denotes the transpose of h and the dotted vari-

ables denote their time derivatives again. The equations

Part E 17.1

Molecular Dynamics 17.1 Basic Idea of Molecular Dynamics 983

Andersen

Parrinello–Rahman

Fig. 17.7 Illustrative images of a deformation of the

periodic boundary cell in the Andersen and the Parrinello–

Rahman scheme

of motion can then be written down by using scaled co-

ordinates s

parameterized as r

= hs

in the following

forms

/dt =h

−1

, (17.35)

/dt =−∂φ/∂r

−

−1t

h p

, (17.36)

h/ dt



Π −P

ext



−1

, (17.37)

where



Π −P

ext



αβ





)

−r

iα

∂φ/∂r

iβ



−P

ext

αβ

(17.38)

is the deviation of the internal from the external stress

tensor.

As schematically illustrated in Fig. 17.7, the dynam-

ical variable ﬁctitiously introduced into the simulation

system is the volume V in the Andersen method,

while its counterpart is the shape tensor h in the

Parrinello–Rahman method; in both of these methods

the periodic simulation cell can change its shape ac-

cording to the dynamical variable V or h. In both

Andersen’s method and the Parrinello–Rahman method,

the coding procedure is carried out by taking the ﬁc-

titious parameters V or h as additional atoms just

like in the Nose–Hoover thermostat method. In ad-

dition, since (17.29–17.33)and(17.35–17.38) contain

velocity-dependent terms, use of a predictor–corrector

method is appropriate. For example, to code the An-

dersen’s constant-pressure method by using the Gear

algorithm, the outline is the following: (Here we shall

also use one-dimensional expression x

(t) for the atom

coordinates and s

(t) = L(t)

−1

(t) for the scaled coor-

dinates for simplicity.)

Step 1 For the p-th order method, specify the ini-

tial (scaled) position s

) and its derivatives



), s



),..., and s

(p−1)

) and assign

them to q

)fori = 1toN.

Step 2 Consider L(t)(orV(t)) as coordinates of the

(N +1)-th atom, specify the initial value for

L(t

)(orV (t

)) and its derivatives, and assign

to q

N+1

Step 3 Calculate the predicted coordinates

+Δt)

for i = 1toN +1 at the ﬁrst step according to

(17.11).

Step 4 Calculate the force F

+Δt) at the ﬁrst step

for i = 1toN according to (17.32) by using

+Δt).

Step 5 Calculate the force F

N+1

+Δt)attheﬁrst

step according to (17.33) by using

+Δt).

Step 6 Compute the corrected q

+Δt) according to

(17.12)fori = 1toN +1.

Step 7 Repeat step 3 to 6 with t

→t

+Δt.

As noted above, there is a risk that the ﬁctitious

variables introduced to control temperature or pressure

might harm the real dynamics of the atoms. In this re-

gard, we shall see how the ﬁctitious variables control the

system pressure in the constant-pressure formalism. In

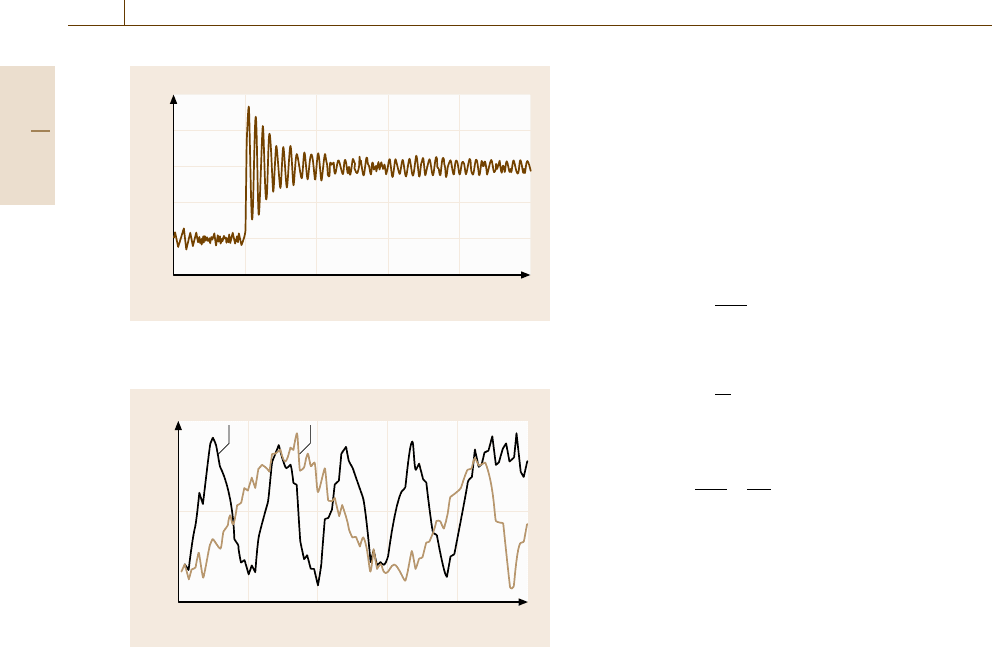
Fig. 17.8, an example of the time evolution of the inter-

nal pressure P =



int



/3 of a simulation

system is shown. The system consists of 4000 atoms

with face-centered cubic (fcc) structure interacting via

a Lennard-Jones potential, which will be explained in

the following section. By using the Parrinello–Rahman

method, the external pressure is changed from 0 to

1GPa at MD time step =2000. Overshooting behav-

ior is found just after the moment at which the pressure

is changed until the pressure settles down around the de-

sired value. This overshooting deviation reaches nearly

1 GPa. A similar behavior could be also found in the

time evolution of the temperature for the Nose–Hoover

thermostat method.

Even after the internal pressure has come to its

equilibrium value there remains a small ﬂuctuation

of the pressure due to the thermal motion of the

simulation cell, as found in Fig. 17.8. This type of

breathing behavior inevitably exists in formulations

using ﬁctitious variables, and its properties strongly

Part E 17.1

984 Part E Modeling and Simulation Methods

1.5

0.5

–0.5

0 2000

4000

6000 8000 10 000

P (GPa)

MD steps

Fig. 17.8 Time evolution of the internal pressure P of the

simulation system

0.05

–0.05

MD steps

0 200 400 600 800 1000

P (GPa)

M=M* M=10 M*

Fig. 17.9 Breathing behavior of the internal pressure P of

the simulation system

depend on the mass of the ﬁctitious variable. For

the same simulation system as shown in Fig. 17.8,

we can calculate the breathing behavior of the inter-

nal pressure P due to the thermal ﬂuctuation in the

cases of different two masses M

∗

and 10M

∗

of the

Parrinello–Rahman cell. (The mass M

∗

will be de-

ﬁned soon.) The results are shown in Fig. 17.9,

where we can see the frequency of the breathing

strongly depends on the mass M of the simulation

cell.

In general, a large mass gives a small overshoot but

a slow convergence, while a small mass gives a large

overshoot but a rapid convergence. In any case, the

dynamics of the atoms in the simulation is inevitably af-

fected by the motion of the ﬁctitious variables [17.13].

In this context, Parrinello suggested [17.14] that the

mass of the simulation cell should be determined such

that the periods of the MD cell oscillation and that

of sound waves are of the same order. The suggested

value is M

∗



/4π

, where m

are the atom

masses.

NPT Ensemble

By combining the temperature-control and pressure-

control methods, we can perform the simulation of

an NPT ensemble, which is most appropriate for

comparison with experimental results under ordinary

conditions. For example, if we take the Nose–Hoover

thermostat method for temperature control and the An-

dersen method for pressure control, the equation of

motions of the total system are the following

/dt

=−

−1

∂φ/∂r

−



−1

S +2L

−1



(17.39)

S/dt

=−





)

−3Nk



−1

, (17.40)

L/ dt

−2







)

−r

·∂φ/∂r



−P

ext



−1

L −2L

−1

, (17.41)

where S is the Nose–Hoover thermostat variable with

amassQ, L is the edge length of the cubic simulation

cell with a mass M in Andersen’s method, and s

are

rescaled coordinates deﬁned through r

= Ls

. A coding

procedure using the p-th order Gear method would be

along the following lines

Step 1 Specify the initial position s

) and its deriva-

tives s



)tos

(p−1)

) and assign them to

)fori = 1toN.

Step 2 Consider S(t)andL(t) as coordinates of the

(N +1)-th and the (N +2)-th atom, specify the

initial values for S(t

)andL(t

) and their deriva-

tives, and assign each to q

N+1

)andq

N+2

respectively.

Step 3 Calculate the predicted coordinates

+Δt)

for i = 1toN +2 at the ﬁrst step according to

(17.11).

Step 4 Calculate the force F

+Δt) at the ﬁrst step

for i = 1toN according to (17.39) by using

+Δt).

Step 5 Calculate the force F

N+1

+Δt)andF

N+2

+Δt) at the ﬁrst step according to (17.40)and

(17.41) by using

+Δt).

Step 6 Compute the corrected q

+Δt) according to

(17.12)fori = 1toN +2.

Step 7 Repeat steps 3 to 6 with t

→t

+Δt.

Part E 17.1

Molecular Dynamics 17.1 Basic Idea of Molecular Dynamics 985

We can also perform a simulation of the NPT en-

semble by combining the momentum-scaling method

for temperature control and the Parrinello–Rahman

method for pressure control. A coding procedure using

the p-th order Gear method is similar to the preceding

case

Step 1 Specify the initial position s

) and its deriva-

tives s



)tos

(p−1)

) and assign them to

)fori = 1toN.

Step 2 Specify the initial values for h

αβ

), that is, the

shape of the simulation cell, and their deriva-

tives, consider h

αβ

(t) as coordinates of the (N +

1)-thtothe(N +9)-th atom, and assign each to

N+1

)toq

N+9

Step 3 Calculate the predicted coordinates

+Δt)

for i = 1toN +9 at the ﬁrst step according to

(17.11).

Step 4 Calculate the force F

+Δt) at the ﬁrst step

for i = 1toN according to (17.35)and(17.36)

by using

+Δt).

Step 5 Calculate the force F

N+i

+Δt)attheﬁrst

step for i = 1 to 9 according to (17.37) by using

+Δt).

Step 6 Compute the corrected q

+Δt) according to

(17.12)fori =1toN +9.

Step 7 Repeat steps 3 to 6 with t

→t

+Δt.

Step 8 Rescale the atomic momenta p

(t)fori =1toN

according to (17.18) after every N

rescale

steps.

17.1.4 Interaction Potentials

The time evolution of the simulation system completely

depends on the forces interacting between atoms, which

are usually derived from interaction potentials. Possible

forms of the interaction potentials popularly used in

simulations will be presented in this section. Among

them, the Lennard-Jones two-body potential and the

embedded-atom method (EAM) many-body potential,

both of which are used repeatedly throughout this chap-

ter, will be given special attention.

The functional form φ(r

, r

,...) of the potential

function plays a crucial role in MD simulation, not only

in the physical aspects but also in the technical aspects

for coding. In this respect, the potential forms can be

classiﬁed into two following categories: two-body po-

tentials and many-body potentials. The former can be

expressed as a sum of functions of atomic distances as

φ(r

, r

,...) =



i, j





−r





. (17.42)

Lennard-Jones Potential

One of the simplest and commonly used two-body

potentials is the m −n Lennard-Jones (LJ) potential,

in which the pairwise interaction between elements

A and B separated by distance r is written as

(r) =e





−







. (17.43)

Here the parameters m and n can be adjusted accord-

ing to the elements in the system and are taken to be

integers in many cases. For example, (m, n) =(12, 6)

is used for rare gasses, while (m, n) =(8, 4) has been

proved [17.15] to be adequate to describe metallic sys-

tems. The potential has its minimum, −e

,atthe

distance r

. Therefore, we can consider these two pa-

rameters as the chemical bond strength and the atomic

size, respectively.

EAM Potential

It is well known that two-body potentials cannot re-

produce the Cauchy discrepancy between the elastic

constants and the correct vacancy formation energy.

A straightforward remedy for the problem is to use

many-body potentials. Among them, one of the most

popular many-body potentials used for metallic systems

is called the embedded-atom method (EAM) [17.16],

which is based on the effective medium theory. In this

framework, the potential energy is written as

φ =



(ρ

) +



i, j

) . (17.44)

Here the ﬁrst term F

(ρ

) corresponds to the energy

required to embed atom i into the electron dens-

ity ρ

, while the second term ϕ

corresponds to

the core-to-core repulsion energy between atom i and

atom j separated by the distance r

expressed in a pair-

wise functional. The sufﬁces A and B denote the species

of the atoms. The former term incorporates the many-

body effect through the electron density assumed to be

a linear superposition



i, j

) , (17.45)

where f

) is the contribution to the electron dens-

ity ρ

at atom i due to atom j at the distance r

The functional forms of f (r)andϕ(r) are deter-

mined so as to reproduce the static properties such as

the cohesive energy, lattice constants, elastic constants,

Part E 17.1

986 Part E Modeling and Simulation Methods

and the vacancy formation energy. For example, simple

exponential forms such as

(r) = f

exp



−β

r/r



, (17.46)

(r) =ϕ

exp



−γ

r/r



, (17.47)

are often used, where f

,ϕ

,β

and γ

are par-

ameters, and r

is the equilibrium nearest-neighbor

distance.

On the other hand, the standard way to deter-

mine the embedding function F

(ρ

)israthermore

complicated. In the original scheme suggested by

Foiles [17.17], the Rose equation of state is used to de-

termine the form of F

(ρ

). The Rose equation of state

is given from the empirical experimental data and shows

the dependence of the cohesive energy of a cubic crystal

on the nearest-neighbor distance r as

(r) =−E



1+α



r/r

−1



−α



r/r

−1



(17.48)

where E

is the cohesive energy with the equilibrium

lattice parameter and the parameter α

is deﬁned as



, (17.49)

using the equilibrium atomic volume Ω

and the bulk

modulus B

of the equilibrium state. By using the

expression (17.44), the embedding function is calcu-

lated as

(ρ) = E

(r) −



)

(17.50)

where the calculation is performed for a cubic lattice

with the nearest-neighbor distance r,andr would be

varied around its equilibrium value r

to obtain the

value of F

(ρ) around the equilibrium electron dens-

ity ρ

From a practical point of view, the value of the elec-

tron density ρ does not signiﬁcantly deviate from its

equilibrium value ρ

. Therefore, a polynomial approxi-

mation around ρ

is sufﬁcient for calculations except for

cases with highly defective structure, such as a surface

structure

(ρ) =



(ρ −ρ

)

, i =0, 1, 2,...,

(17.51)

where the coefﬁcients F

are determined so as to repro-

duce the experimental properties.

According to the tight-binding theory, another func-

tional form F(ρ) has also been suggested. Up to the

second-moment approximation, the functional form of

the embedding function is evaluated as

F(ρ) = F



ρ/ρ

. (17.52)

This type of potential is called the Finnis–Sinclair po-

tential [17.18] and has been widely used in simulations

of metallic systems.

Cutoff Procedure

Since the functional forms found in (17.43–17.47)have

an inﬁnite interaction range, we usually make a cutoff

termination to the potential functions to decrease the

calculational cost in MD simulations. For each func-

tion to be modiﬁed, we set both the starting distance

where the termination starts and the cutoff distance

where the modiﬁed function vanishes.

The two typical terminating processes are as fol-

lows. One is to exchange the potential function with

a cutoff function g

(r)forr > r

, which is continuous

at r

to the potential function up to the second deriva-

tive, and vanishes for r > r

. For the choice of g

(r),

a polynomial form is often taken

(r) =



(r −r

)

, for r

< r < r

, (17.53)

where the parameters c

are determined to satisfy

continuity at r

to the potential function up to the

second derivative, and i = 2, 3, 4, 5,... For exam-

ple, a modiﬁed LJ potential with terminating at

the third-order polynomial starting at its inﬂection

point is called the LJ-spline potential. For the case

(m, n) = (8, 4), which we shall use in the follow-

ing sections, the parameters in (17.53) are uniquely

determined as c

=−(10 240/3159)(5/9)

(1/2)

−2

, c

−(655 360/369 603)(5/9)

(3/4)

−3

, and the terminating

position r

=(103/64)r

∼1.864r

by requiring conti-

nuity to the potential function up to the second deriva-

tive at the inﬂection point r

= (9/5)

(1/4)

≈ 1.158r

For a smoother cutoff at r

, the fourth-order function

(i = 3, 4) would be used.

The other approach is to multiply by a switch-

ing function g

(r) that satisﬁes the properties g

)

= 1, g



) = g



) =0, and g

) = g



) = g



)

=0 to the potential function on the interval [r

, r

]. For

example, if we take a polynomial function

(r) =



(r −r

)

, for r

< r < r

(17.54)

of ﬁfth order, that is, i = 3, 4, 5, then the coefﬁ-

cients in (17.54) are determined as d

=10(r

−r

)

−3

Part E 17.1

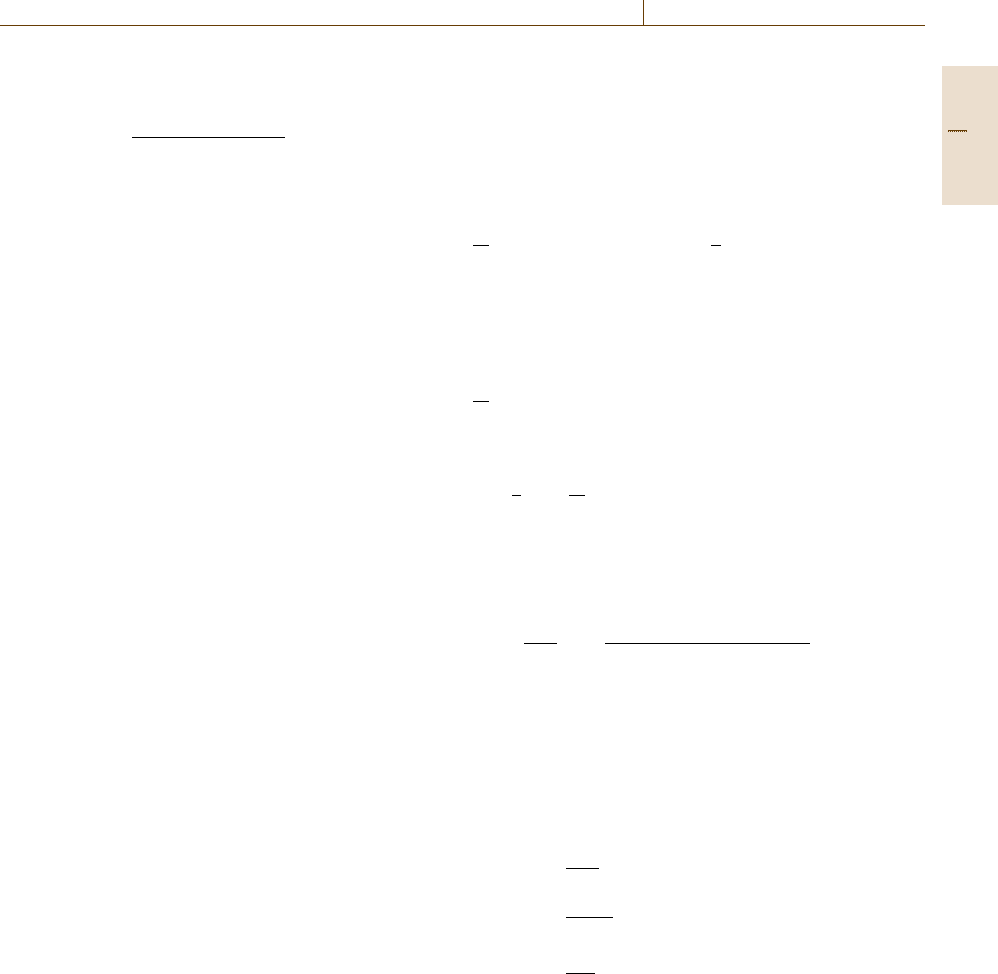
Molecular Dynamics 17.1 Basic Idea of Molecular Dynamics 987

=−15(r

−r

)

−4

,andd

=6(r

−r

)

−5

. An expo-

nential form such as

(r) =exp



(r −r

)

(r −r

)

−(r

−r

)



, (17.55)

can be also used for the switching function.

17.1.5 Physical Observables

The method of extracting physical observables will be

explained in this subsection. Various observables can be

calculated by the MD simulations, including volume,

energy, pressure, elastic moduli, diffusivity, viscosity,

radial distribution function, etc. Here only formulas for

evaluating the observables are shown in this section,

while the examples applied to the actual MD simula-

tions will appear in later sections.

Thermodynamical Properties

In the course of the MD simulation, thermodynamical

properties such as the total volume V and the inter-

nal energy E are always calculated, so they are easy to

monitor. The internal pressure P of the simulation sys-

tem can also be monitored by using (17.23). In ordinary

MD simulations, we consider a long-time average of the

thermodynamical properties as an ensemble average





ensemble





time

. (17.56)

In the actual estimation of these observables, we usu-

ally take an average over 100–10 000 time steps, among

which the longer time averages reduce the effect of

thermal ﬂuctuations and statistical errors. Other ther-

modynamical properties, such as the speciﬁc heat or

the thermal expansion rate, can be estimated from the

change of E and V with T or P.

Structural Properties

The radial distribution function provides a lot of in-

formation about atomistic structure. It can be directly

calculated from the atomic coordinates r

(t). In many

cases, by taking a time average of the pair distribution



i, j





(t)−r

(t)





, (17.57)

we can greatly reduce the effect of thermal vibrations.

Microscopic structural properties such as the num-

ber of atomic pairs or local symmetry properties around

each atom also yield important information [17.19].

One of the popular methods used to investigate the mi-

croscopic structure is Voronoi polyhedra analysis. Some

examples will be given in Sect. 17.3.2.

Dynamical Properties

Among the dynamical and transport properties, the

diffusivity is easy to estimate because we know the

position of all atoms. That is, we can estimate the self-

diffusion coefﬁcient D from the linear part in the time

evolution of the mean square displacement of the atoms







) −r

+t)





Dt +const. ,

(17.58)

where the time average ··· starts from the initial

time t

. The diffusivity D can be also calculated from

the zero mode of the velocity autocorrelation function





) ·v

+t)



(17.59)

D =

∞







)·v

+t)





)

(17.60)

In the same manner, the viscosity η

αβ

can be estimated

from the stress autocorrelation function as

αβ

∞





V(t

)





αβ

+t)



αβ

)

(17.61)

where the stress tensor P

αβ

is found from (17.23), and

the Greek symbols take the Cartesian values 1, 2, or 3.

Elastic moduli can be calculated [17.20] from a ther-

modynamical ﬂuctuation formula. From a long-time

average of the ﬂuctuation of the stress tensor P

αβ

,the

adiabatic elastic coefﬁcients C

αβ;γδ

can be calculated as

αβ;γδ

=−







αβ

γδ

−



αβ



γδ









αδ

βγ

+δ

αγ

βδ











i, j



−2



∂

φ/∂r

−r

−1

∂φ/∂r



× r

ijα

ijβ

ijγ

ijδ

, (17.62)

where δ

αβ

is the Kronecker delta, and k

is the Boltz-

mann constant.

The vibration modes of atomic motion can also be

calculated from the velocity autocorrelation (17.59); ex-

amples will appear in Sect. 17.3.2.

Part E 17.1