Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing

Подождите немного. Документ загружается.

948 Part D Materials Performance Testing

Excitation signal (V)

= d/t

–10

0 1.00.80.60.4 1.20.2

–10

0 1.00.80.60.4 1.2

Time (ms)

0.2

Lamb wave response (mV)

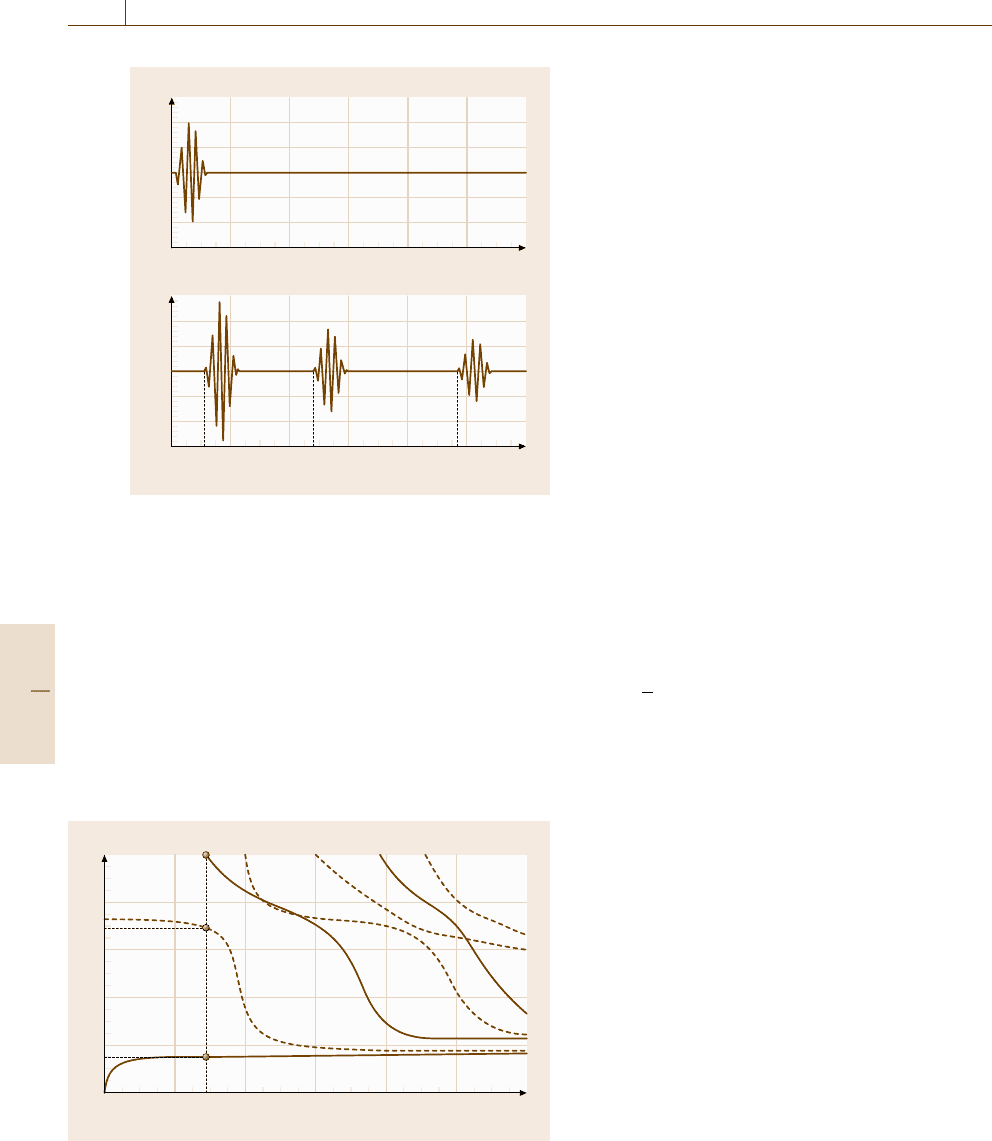
Fig. 16.99 Example of an excitation signal (upper)and

a multimode response

troduced a third solid deﬁned as a thin layer of ﬁnite

thickness. This allowed the study of wave propaga-

tion in multilayered materials, such as in composites.

The waves propagating in this multilayered mater-

ial were then called Lamb waves. The term Lamb

waves refer to elastic waves propagating in a solid

plate with free boundaries. The displacements of the

Lamb waves occur both in the direction of the wave

propagation and perpendicularly to the plane of the

plate. A comprehensive description of physical the-

Phase velocity (km/s)

λ =41mm

λ =28mm

λ =6mm

21.61.20.80.40 2.4

Frequency by half thickness (MHz mm)

1.5

0.58

6.9

Fig. 16.100 Phase velocity for the cross-ply laminate [0

/90

ory and application of Lamb waves can be found

in [16.97].

Lamb waves consist of several waves γ

of the same

waveform γ that propagate with different propagation

velocities ν

called the group velocities. The waveform

is often called a mode. Each Lamb wave mode can

propagate symmetrically or antisymmetrically within

the laminate, as shown in Fig. 16.98.

The amplitude of γ

depends on the composite

used. Up to now no theory exists that can exactly pre-

dict the amplitude of the Lamb waves. Figure 16.99

shows an example of multimode signal containing three

modes [16.97]. The time t

is the time of ﬂight of the

Lamb wave mode γ

. In the present case, the Lamb wave

generator and receiver are separated by a distance d.

The response given in Fig. 16.98 does not correspond

in detail to Lamb waves, because a real Lamb wave

response would be too complex for the educational pur-

pose of this section.

Indeed, a Lamb wave response would include not

only the Lamb wave modes but also their reﬂec-

tions, which do not exist in the multimode response

of Fig. 16.99. Besides, it is possible that at the excitation

frequency, some Lamb wave modes might be dispersive,

meaning that their corresponding waveform may not be

similar to the waveform of the excitation signal. The

group velocity v

of the mode γ

is given by

. (16.37)

However, the number of waveforms, or modes, prop-

agating in a laminate as well as their time of ﬂight

can be predicted by the dispersion curves. Two types

of dispersion curves are mostly used for the Lamb

wave technique: the phase velocity c and group veloc-

ity v, as shown in Figs. 16.100 and 16.101, respectively.

The phase velocity corresponds to the ratio of the

spatial component, i. e. the wavenumber ξ,tothetem-

poral component, i. e. that is the angular frequency

ω =2π f , of a harmonic wave. The group velocity may

be described as the energy velocity of the Lamb wave

modes in relation to the laminate. The phase-velocity

curves are mainly used to determine whether or not

the Lamb wave modes will be dispersive, and also to

obtain the wavelength λ of each Lamb wave mode

generated in the laminate, using the following relation-

ship

λ =c/ f , (16.38)

where f is the frequency spectrum of all Lamb wave

modes generated in the laminate. To ﬁnd out if a Lamb

Part D 16.6

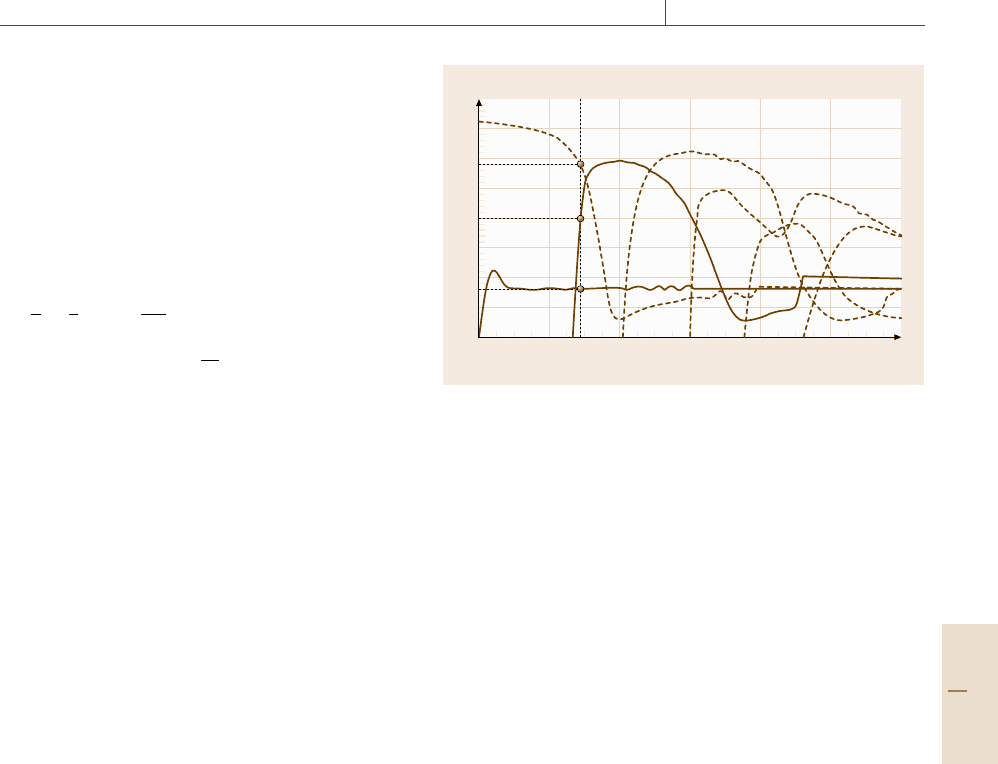
Performance Control 16.7 Characterization of Reliability 949

wave mode is dispersive or not, the derivative of the

phase velocity is used. If, at a given excitation fre-

quency, the derivative of the phase velocity is zero,

then the Lamb wave modes should be nondispersive.

Most of the time, nondispersive Lamb waves are cho-

sen, because their corresponding waveforms generally

remain the same throughout the propagation. Moreover,

the phase and group velocities of a nondispersive wave

are theoretically identical. Indeed, both velocities are

governed by the following equation



1 − f

d f



. (16.39)

For a nondispersive wave

d f

=0 and therefore (16.39)

leads to v = c.

The wavelength of each Lamb wave mode is di-

rectly related to the sensitivity of the Lamb waves to the

detection of damage. In principal a Lamb wave of wave-

length λ is able to interact with damage on the order of

or greater than λ. The dispersion curves depend on the

composite material and lay out used. Often the disper-

sion curves are given as a function of the product fh

(frequency by half laminate thickness). Two examples of

dispersion curves are given in Figs. 16.100 and 16.101,

for a stacking sequence of [0

/90

]s and the

composite material HTA/6376C. In the ﬁgures, S and

A stand for symmetric and antisymmetric modes, re-

spectively, and the subscript corresponds to the mode

number.

The dispersion curves are important for charac-

terizing the active system that detects damage in the

composite [16.98]. The frequency spectrum of all Lamb

wave modes is, in principal, equal to the frequency

spectrum f of the excitation signal of the Lamb wave

generator. In the example shown in Fig. 16.101,the

frequency of the excitation signal is 240 kHz for a com-

posite thickness of 4.83 mm. Figure 16.101 therefore

shows that the only Lamb wave modes that can exist in

Group velocity (km/s)

21.61.20.80.40 2.4

Frequency by half thickness (MHz mm)

1.6

0.58

5.8

Fig. 16.101 Group velocity of Lamb waves propagating in the lam-

inate [0

/90

this composite would be the modes A

, S

and A

with

group velocities of 1.6km/s, 5.8km/sand4km/s, re-

spectively. Figure 16.100 further allows determination

of the wavelengths of those modes A

, S

and A

,which

are about 6, 28 and 41 mm, respectively. In such an ex-

ample, the mode A

would be able to detect damage

of at least 6 mm or larger, with the condition that its

amplitude is large enough for the mode to be meas-

ured. Note that for higher frequencies, the wavelength

of the mode A

, for example, is smaller than 6 mm. This

would therefore allow the detection of damage smaller

than 6 mm. Unfortunately, the propagation distance of

the Lamb wave modes tends to decrease with increasing

frequency.

Several developments have occurred in this area

since the technique was ﬁrst reported, which have led

to new possibilities and advances in the capabilities of

structural health monitoring [16.99, 100]. Special fo-

cus has been given to the monitoring of composites for

aircraft applications [16.101].

16.7 Characterization of Reliability

Reliability is a statement of whether or not a device

fulﬁlls its function after a certain time of operation.

The scientiﬁc deﬁnition of reliability reads as fol-

lows [16.102]: Reliability is the probability that an item

will perform a required function without failure under

stated conditions for a stated period of time.

As the lifetime of a device scatters, reliability is

a quantity that can only be described by means of

statistic tools, which will be introduced brieﬂy in the

ﬁrst Sect. 16.7.1. Additionally, we will show that the

scatter in lifetime originates from the scatter of both

the strength of the device and the scatter of the stresses

to which it is exposed. Both can be described by dis-

tribution functions, and the region of interference of

both distributions will be shown to be a measure for the

failure probability.

Part D 16.7

950 Part D Materials Performance Testing

In Sect. 16.7.2, the Weibull analysis will be intro-

duced, as it has become the major tool in science and

industry to analyze failure data. Due to the importance

of this issue, this section is the longest in this chap-

ter.

Section 16.7.3 will show different test strategies.

Those address the basic problem of how to character-

ize reliability with a small number of sample devices

with the smallest possible time effort.

A similar question is addressed in Sect. 16.7.4,in-

troducing the important acceleration techniques. The

basic idea is to apply higher stresses to the device than

under real-life conditions to provoke failures. By means

of physical models describing the degradation process,

the lifetime under real conditions can be estimated.

In the last Sect. 16.7.5, quantitative reliability esti-

mation for complex systems will brieﬂy be discussed.

The failure behavior of a complex system consisting

of single components can be calculated from the com-

ponent reliabilities. Here, we restrict discussion to the

simple case where the system solely consists of compo-

nents with serial and parallel functionality.

In this chapter, special emphasis will be placed on

the following

•

enabling the reader to become familiar quickly with

the basic concepts of reliability

•

restricting discussion to the main tools presently

used in science and industry.

For further reading, key literature is given. To com-

pletely understand this material it is inevitable that

more-sophisticated literature, which deals with special

topics in more depth than is possible here, will have to

be consulted.

There are some standard textbooks available that

introduce the basic concepts. Some of them have hand-

book character and are designed for daily use in

practice [16.102–106]. Others emphasize the mathe-

matical background and statistical tools [16.107].

Also there are several websites available dealing

with reliability. Some of these websites, e.g. [16.108,

109], offer excellent tutorials and introductions to re-

liability. Further websites are found in the survey

paper [16.110].

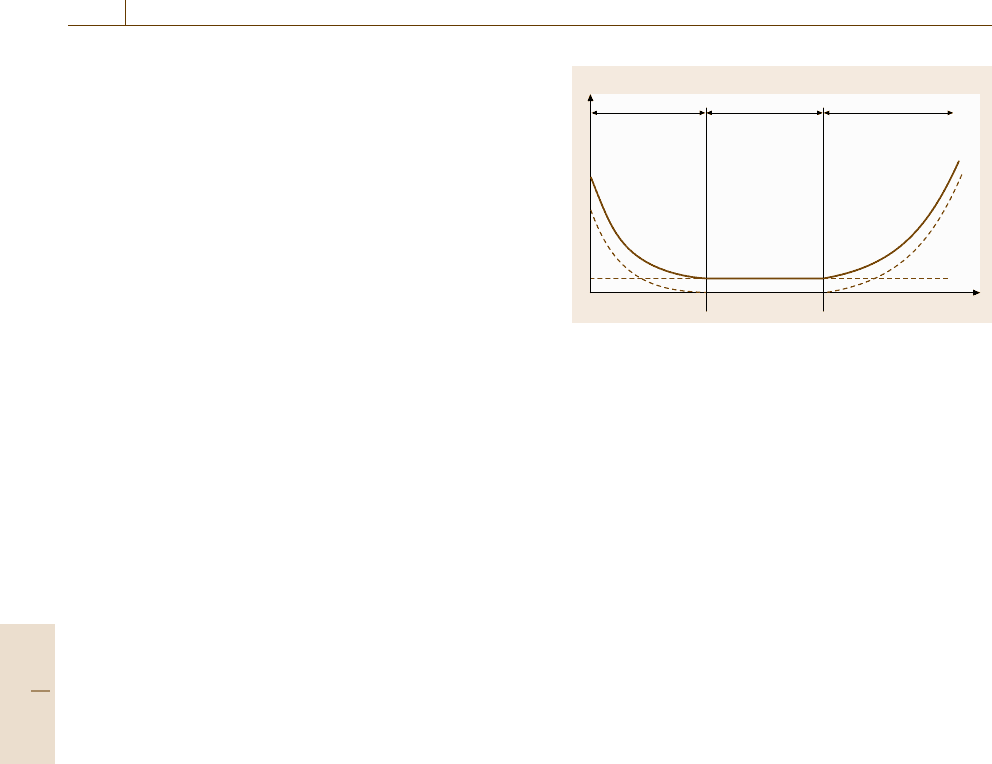
The Bathtub Curve

In order to describe the time dependence of a device’s

failure behavior, a reliability parameter called the failure

rate λ(t) rate is used. Simply speaking, this describes

the (average) number of failures per time unit. An exact

deﬁnition will be given in the next section.

λ (t)

Early

failures

Random

failures

Wear-out

failures

Region 1 Region 2 Region 3

Fig. 16.102 The typical bathtub curve (thick line), as a su-

perimposition of the three failure rates belonging to

independent failure mechanisms dominating in the regions

1–3 (dashed lines)

In most cases, if λ(t) is plotted against time, a typ-

ical bathtub shaped curve is observed (Fig. 16.102)

[16.102,111].

The bathtub curve is categorized into three regions.

•

Region 1 exhibits a falling failure rate and covers

the so-called early failures (infant mortality). The

origin of those failures in most cases is not related

to material properties, but rather to the quality of the

manufacturing process of the whole device.

•

Region 2 is characterized by a constant failure rate

and covers random failures that are not governed by

a single failure mechanism. In this region, the de-

vice fails due to miscellaneous interactions with its

environment, e.g. peak-like overloads, misuse, high

temperatures and others.

•

Region 3 is the region where material-related fail-

ures start to dominate. Therefore, the somewhat

imprecise phrase wear-out failures is commonly

used for this phase. The failure modes in this re-

gion are often initiated by detrimental changes of

the devices’ material components, caused by the ser-

vice loads applied to the device. The mechanisms

leading to failures are called degradation mecha-

nisms. Those mechanisms lead to a strong increase

of the failure rate with time. Typical degradation

mechanisms are mechanical fatigue (Chap. 7), cor-

rosion (Chap. 12), wear (Chap.13), biogenic impact

(Chap. 14), and material–environment interactions

(Chap. 15).

A very important statement is that the Weibull analysis

(Sect. 16.7.2) enables us to judge to which category the

investigated product belongs using the failure data anal-

ysis.

Part D 16.7

Performance Control 16.7 Characterization of Reliability 951

16.7.1 Statistical Treatment of Reliability

Since reliability is deﬁned as a statistical quantity, sta-

tistical tools are needed to describe it. In the following

section, the origin of the statistical scatter will be de-

scribed by means of static and dynamic stress–strength

interference models. In the following section, reliabil-

ity functions and reliability parameters describing the

time-dependent failure behavior are introduced.

Reliability Functions

For a given time value t, F(t) describes the probability

for the event that the device will fail within the time

interval between 0 and t.

To describe this quantitatively, we introduce the life-

time L of the device. L may be given in unit of time,

cycle number, or any other quantity related to the life of

the device. Then the failure probability F(t)isdeﬁned

as the probability P that L is smaller than or equal the

observation time:

F(t) = P(L ≤ t) . (16.40)

F(t) may also be written as integral over its failure

density f (t)

F(t) =



f (t



)dt



. (16.41)

The failure density function has practical meaning,

since distribution functions are commonly given in this

expression. As an example, the well known bell-shaped

curve is the density function of the Gaussian normal

distribution, but not the distribution function itself.

Given the failure probability, the probability of sur-

vival is expressed as its complement R(t). R(t) is called

the reliability function, or simply the reliability

R(t) =1−F(t) =1 − P(L ≤ t) = P(L > t) .

(16.42)

The failure rate, which was introduced earlier in a qual-

itative manner, can now be deﬁned precisely as

λ(t) =

f (t)

R(t)

(16.43)

and describes the probability that the device survives

until t +dt under the condition that it already survived

until t.

Figure 16.103 presents all these functions within

one schematic diagram.

Stress–Strength Interference

The time dependence of the failure probability origi-

nates from both the interaction of the statistical scatter

of the applied stress and the statistical scatter of ma-

terial properties determining the macroscopic strength

(Sect. 7.3) of the component under load [16.112]. In

this context, stress means any physical process acting

on the device, for example mechanical stress, volt-

age, temperature or humidity. Strength, on the other

hand, means the ability of the device to withstand

the stress. Both quantities have the same physical

dimension and are here – in accordance to me-

chanical stress and strength – generally described

by σ.

•

The strength σ

(S =strength) scatters due to scat-

ters of manufacturing quality and due to scatters of

the material properties.

•

The stress σ

(L =load) scatters due to different

users and due to varying use conditions.

f(t)

Failure density

function

Failure function

Reliability function

Failure rate

Time

R(t)=1–F(t)

λ(t)=f(t)/R(t)

F(t)=

f (t')dt'

∫

Fig. 16.103 Schematic drawing of all four relevant func-

tions discussed in Sect. 16.7.1. In particular, the relation

between the failure density function and the other functions

is shown

Part D 16.7

952 Part D Materials Performance Testing

Failure takes place as soon as the stress exceeds the

strength. The failure probability is therefore depen-

dent on the probability that a randomly chosen stress

condition exceeds the strength of a randomly chosen

device. This probability is dependent on the overlap of

the distribution functions, as illustrated in Fig. 16.104a

showing the so-called static stress–strength interfer-

ence.

The area under both curves is calculated as [16.112]

F = P(σ

>σ

) =

∞



−∞

(σ)

⎡

⎣



−∞

(σ)dσ

⎤

⎦

dσ

(16.44)

where f

and f

are the density functions of the distri-

butions of the stress and the strength, respectively.

F(t)

0.5

S = Strength

L = Load

Fig. 16.104 (a) Static, and (b) dynamic interference model.

The failure probability of a device depends on the area

under the distribution densities for stress and strength (af-

ter [16.102, 113])

The same argumentation holds for the dynamic

interference model (Fig. 16.104b). Here, the failure

probability is zero at t = 0 since the overlap of both

distribution functions is negligible. Then, during the

time of operation, microstructural changes within the

material reduce the mean value of the strength and

so F increases signiﬁcantly with increasing operation

time.

The interference model has the great advantage

that it describes the probabilistic origin of time-

dependent failure probabilities in a plausible manner.

However, it is not suitable for determining the reliabil-

ity of a device quantitatively, because the application

of (16.44) requires the exact knowledge of the dis-

tribution functions of stress and strength near their

tails. This demand is usually improperly fulﬁlled in

practice.

16.7.2 Weibull Analysis

One of the main topics in reliability engineering is to

analyze a given set of failure data. These data may

originate from a reliability test performed in the lab

or from a warranty analysis of ﬁeld data. The Weibull

analysis makes use of the famous and widely used

Weibull distribution, and has became the major tool in

modern industry. Many publications document the im-

portance of this tool [16.104]. It should be mentioned

that there exist other distributions which are also impor-

tant. Especially in the case of degradation and fatigue

strength phenomena, the lognormal distribution is im-

portant [16.114,115]. In [16.116], the author compared

the pros and cons of both distributions for the analy-

sis of wear-out (region 3 of the bathtub curve) failure

data.

The Weibull Distribution Function

The Weibull distribution is a multipurpose distribution,

which by varying the independent parameters, can be

adjusted to almost every failure behavior. The failure

function F(t) and the failure density function f (t)of

the Weibull distribution read as follows [16.104,117]

F(t) =1− e

−





, (16.45)

f (t) =





β−1

−





. (16.46)

The reliability function R(t) =1 −F(t)isgivenby

R(t) = e

−





. (16.47)

Part D 16.7

Performance Control 16.7 Characterization of Reliability 953

The Weibull distribution has the following parameters.

•

The shape parameter β (also called the Weibull pa-

rameter or slope),

•

The characteristic life η.

(An additional parameter, the failure free time, will be

introduced later in this section.)

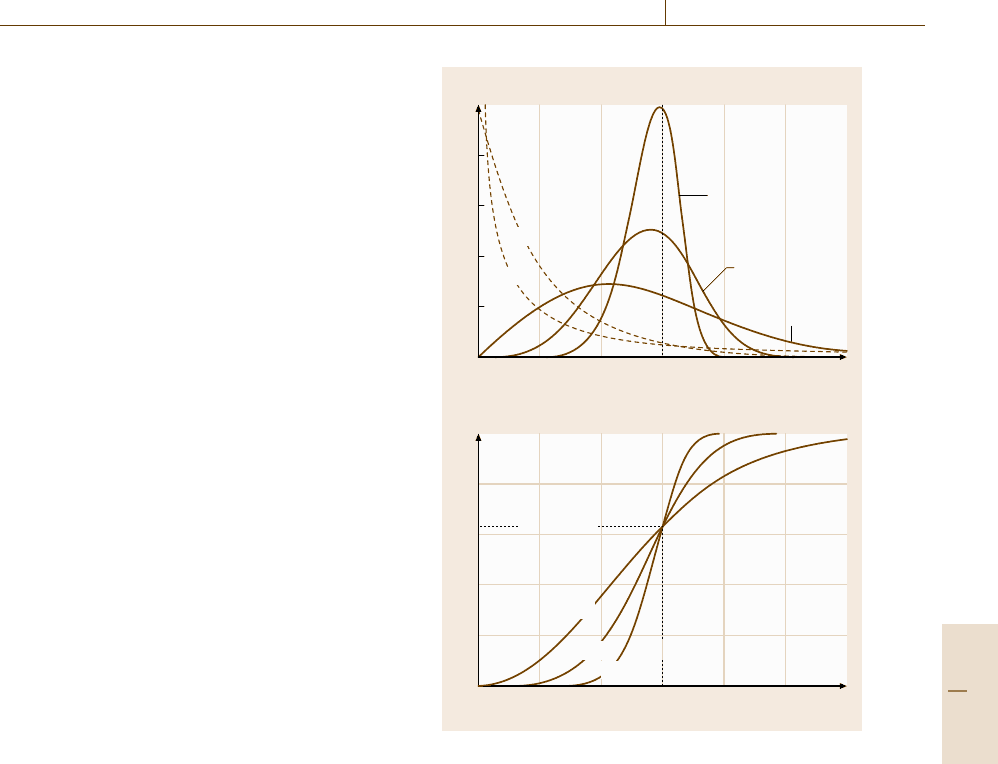
The most important parameter is the shape parame-

ter β, since the distribution can be adapted to the given

failure phenomenon by varying β.InFig.16.105,the

density function and the failure function are plotted for

constant η and different β, showing that the characteris-

tics are different for different β.

A very important result is that the value of the shape

parameter corresponds to the three regions of the bath-

tub curves as follows (Fig. 16.102).

1. β<1 – corresponds to region 1 of the bathtub curve,

since β<1 results in a decreasing function in the

failure rate plot.

2. β =1 – corresponds to region 2 of the bathtub curve,

since β =1 results in a horizontal line in the failure

rate plot. For β = 1, the Weibull distribution be-

comes an exponential distribution function,which

is an important special case. The fact that the fail-

ure probability is independent of time is represented

in the term memory loss. As an example, electronic

devices often show such a time-independent failure

behavior.

3. β>1 – corresponds to region 3 of the bathtub curve,

since β>1 results in an increasing failure rate

function. For β>1, the density function exhibits

a maximum value, and for β ≈ 3 it is similar to the

Gaussian bell-shaped curve (compare Fig. 16.105).

Weibull Analysis Procedure

In the previous section, we outlined the importance of

determining the Weibull parameters in order to catego-

rize the failure phenomena. In this section, it will be

described how the parameters η and β are determined

from a given set of failure data.

Two common methods for Weibull analysis are

known. The ﬁrst one is the so-called median rank re-

gression (MRR), the other one is maximum-likelihood

estimation (MLE).

The latter is a numerical method that needs intensive

computation, while the ﬁrst one is more instructive and

often used. Therefore, we will restrict the discussion to

the MRR here.

The median rank Weibull analysis MRR contains

the following steps.

Density f (t)

Failure probability F (t)

0.8

0.6

0.4

0.2

Lifetime t

54321

0.8

0.6

0.4

0.2

Lifetime t

F = 63.2 %

54321

β =1

β =8

β =4

β =2

β =8

η =3

β =4

β =2

β =0.5

Fig. 16.105 Weibull density function (a) and failure prob-

ability (b) for different β and η = 3. From the density

function plot, we see that a bell-shaped curve is only

reached for β>1. In the case β<1, no local extrema are

present. From the probability plot, we see the peculiarity

that the characteristic life is independent of β

Step 1: Collecting Lifetime Data. n samples are tested,

yielding n lifetimes L

, L

,...,L

. The lifetimes L

the specimen are arranged in ascending order in a table

(Table 16.10).

Step 2: Median Rank Calculation. This is the procedure

that is characteristic of this method. The basic idea is

that each sample is assigned a failure probability F(L

This is necessary, since from the experiment we only

know the lifetime data L

but not the corresponding fail-

ure probabilities. This probability cannot be determined

experimentally, but must be found from theoretical con-

siderations. The understanding of its derivation is not

Part D 16.7

954 Part D Materials Performance Testing

essential for proceeding; however, the interested reader

may ﬁnd it in [16.103]. At this point, one hint is helpful:

The failure probability F(L

) itself follows a statistical

distribution known as the binomial distribution. Since

the binomial distribution cannot be rearranged such that

F(L

) can be calculated directly, some approximation

must be introduced.

In the literature, a vast amount of different meth-

ods for approximating the failure probability is known,

but the formula for median ranks introduced by Be-

nard [16.102, 103] has turned out to be the most often

used. This formula reads

50%

) ≈

i −0.3

n +0.4

. (16.48)

The index 50% indicates that the median of the failure

probability distribution is meant.

Instead of calculating the values using (16.48), they

can also be looked up in tables for median ranks [16.102].

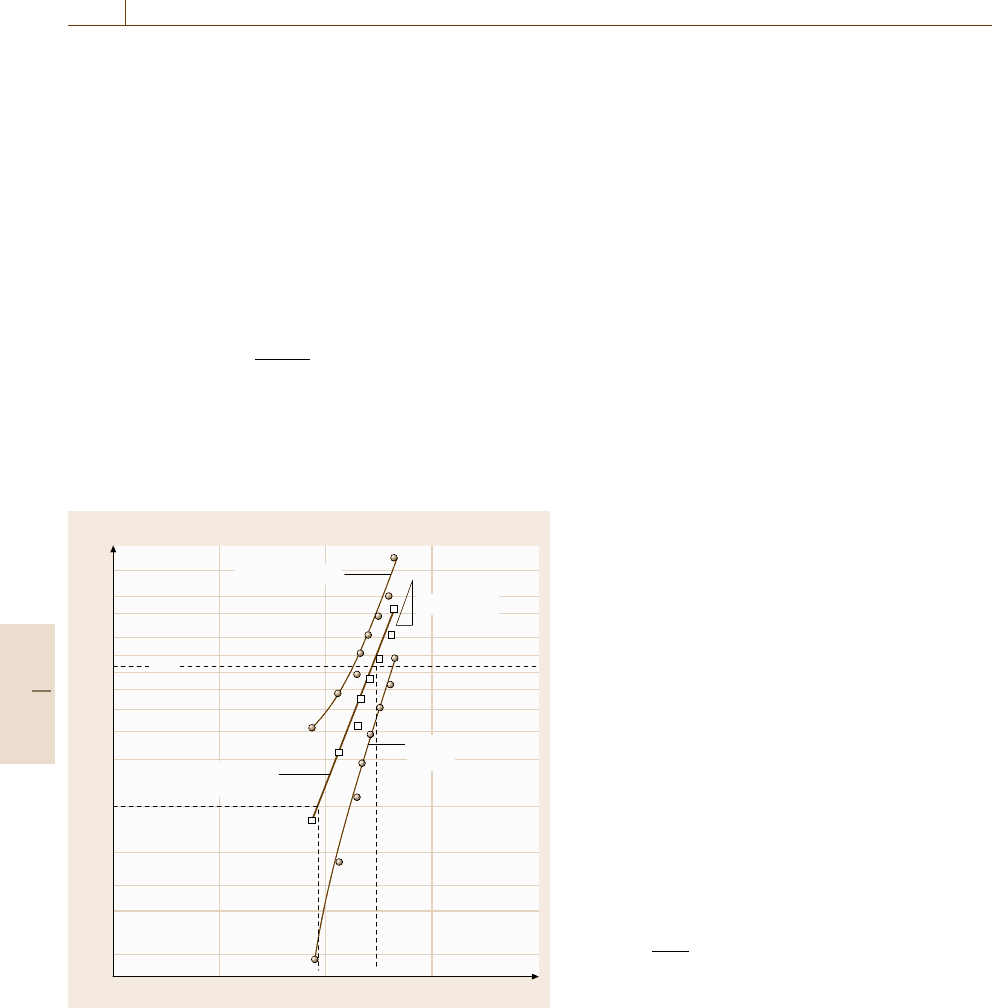
Failure probability F(t) (%)

99.9

63.2

Lifetime (log)

Weibull line

β = Δy/Δx

5 % confidence

bound

95 % confidence

bound

(50 % percentile line)

Fig. 16.106 Schematic drawing of a Weibull plot. The square data

points show the measured lifetimes and the corresponding median

ranks F(L

). The darker circles represent the 5% and 95% con-

ﬁdence bounds. The Weibull parameter β is estimated from the

slope of the weibull line, the characteristic life is estimated from

the intersection of the regression Weibull line with the 63.2% line.

Additionally, we ﬁnd the so-called B

life as the lifetime where

F =10% is reached

An excerpt of such a table is given in the appendix to this

chapter for different sample sizes up to n =12.

Step 3: Probability Plotting. The probabilities of failure

are plotted against the lifetime or number of survived

cycles on so-called Weibull paper, what can be seen

in Fig. 16.106 for the example n = 8. Weibull paper is

commercially available, or can be constructed by the

method described in [16.116]. If the data points obey

the Weibull distribution, then they yield a straight line

with little scatter of the data points. The straight line

is also plotted on the Weibull paper, and will serve to

determine the parameters β and η.

Step 4: Linear Regression. Equation (16.45) is rear-

ranged as follows by taking the double logarithm of

both sides of the equation:

F(L

) =1 −exp(L

/η)

⇒1−F(L

) =exp(L

/η)

⇒ln{−ln[1−F(L

)]}=β ln(L

) −β ln η.

(16.49)

With the general linear equation y = Ax + B we can

now identify

=ln{−ln[1 −F(L

)]}; x

=ln L

(16.50)

and

A =β ; B =−β ln η. (16.51)

These equations allow the determination of the good-

ness of ﬁt and the Weibull parameters β and η,whichis

described in the following.

Step 5: Estimation of the Goodness of Fit: the Correla-

tion Coefﬁcient (CC). In the case of a Weibull-distributed

basic population, a straight line is produced in the

Weibull plot. If the data do not obey a linear behavior,

the basic population may not be Weibull distributed. As

a measure for the linearity of the data, the correlation

coefﬁcient (CC), which is well known from standard

statistic tools [16.118,119], is commonly used. The CC

is deﬁned as

CC =

, (16.52)

where σ

is the covariance and σ

and σ

are the stan-

dard deviations of the x

and y

, respectively.

By calculating x

and y

from the values F(L

)and

in Table 16.10 by means of (16.50), we can apply the

CC to the obtained data pairs. CC takes a value between

0 and 1, and the higher CC, the better is the ﬁt.

Two problems arise when applying CC.

•

It is left to the judgement of the user to decide what

correlation coefﬁcient means a good or a poor ﬁt.

Part D 16.7

Performance Control 16.7 Characterization of Reliability 955

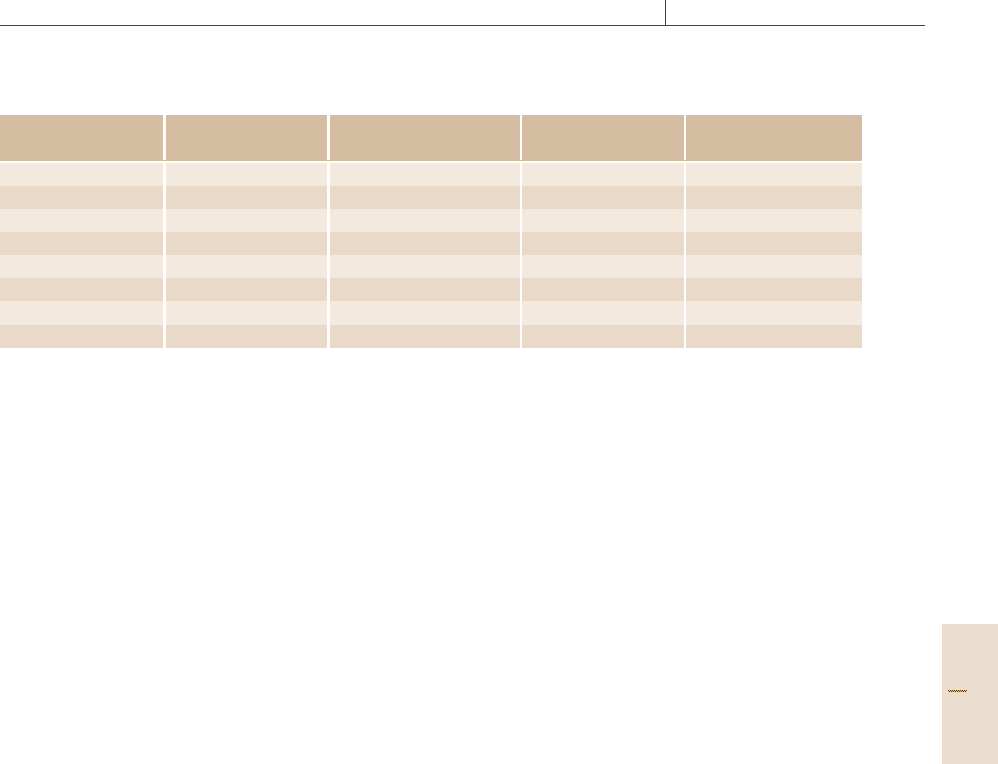
Table 16.10 Measured lifetime data L

and median failure probabilities F

50%

), as well as the F

and F

95%

percentiles needed for the conﬁdence bound, which is introduced in Step 7

Sample # i Lifetime L

50%

) F

95%

=((16.48) or Appendix) (Appendix) (Appendix)

1 L

8.3 31.2 0.6

2 L

20.1 47.1 4.6

3 L

32.1 59.9 11.1

4 L

44 71.7 19.3

5 L

55.9 80.7 28.9

6 L

67.9 88.9 40

7 L

79.8 95.4 52.9

8 L

91.7 99.4 68.8

A possible approach to overcome this problem is

shown in [16.120].

•

The regression of the y-values versus the x-values

is somewhat unsatisfactory and overestimates the

goodness of the ﬁt because the y-values are pre-

determined by the rank calculation. In contrast, the

measured lifetime values are in fact the values that

show scatter. Therefore, Abernethy [16.104] recom-

mends doing the regression of x versus y.

In standard mathematical calculation software, linear

regression is a standard tool and the calculation of the

correlation coefﬁcient CC – sometimes also denoted by

the symbol R – is also standard.

It should be mentioned that there are some other,

more sophisticated and more accurate tests avail-

able such as the Chi-squared test and the tests by

Kolmogorov–Smirnov and Mann–Scheuer–Fertig (see

references in [16.116]), however, for daily practical ap-

plication, CC appears to be the easiest and quickest

method.

Step 6: Determination of η and β. From the linear

regression performed in Step 4, η and β can easily be

calculated by applying (16.51)

β = A ; η = exp(−B/β) . (16.53)

The characteristic life can also be directly determined

from the Weibull plot in Fig. 16.106. If we introduce

t = η in (16.45), we obtain F(η) =63.2%.

Therefore, the Weibull line crosses the F = 63.2%

line at t = η. This is indicated in Fig. 16.106 by an ar-

row.

The slope β can be determined graphically only if

a special, commercially available Weibull paper is used

for the graphical analysis [16.108]. In addition to the

paper used in Fig. 16.106, this paper has a second y-axis

where β can be found by a method described in [16.103]

and [16.108].

Step 7: Introducing the Conﬁdence Interval α. The

conﬁdence interval α is a very important parameter. The

conﬁdence bound is a demand given from the user of

the Weibull analysis, representing his demands on the

trustworthiness of the analysis.

In many practical cases, the conﬁdence interval of

α = 90% is demanded. If α = 90% holds, then the up-

per and lower conﬁdence bounds are the 95% and 5%

percentiles. Similar to the 50% percentiles, these values

can be found in the tables given in Step 3. These values

are added to the two columns F

and F

95%

in the ta-

ble. These values can then also be plotted in the Weibull

graph (Fig. 16.106).

The meaning of the conﬁdence bounds is as follows.

To require a conﬁdence level of, e.g., α =90%, means

that the probability that the true Weibull regression line

lies within the conﬁdence bounds is 90%. In Fig. 16.106

this demand can be found by noting that any Weibull

line that is compatible with the conﬁdence bounds is

a possible solution to our problem.

To avoid frequent misunderstanding, it should be

mentioned that the width of the conﬁdence bound does

not depend on the scatter of the measured lifetime data.

The width of the conﬁdence bound solely depends on

the number of specimen tested. The larger n, the smaller

the conﬁdence bound becomes. This is logical, since the

signiﬁcance of the statistical argumentation becomes

higher with increasing sample size.

Step 8: Estimation of the Conﬁdence Bounds of β

and η. Since the conﬁdence bounds determined in

Step 7 lead to more than one possible Weibull line,

we also ﬁnd a range of values for β and η which we

need to determine. To do so, one possibility is to de-

Part D 16.7

956 Part D Materials Performance Testing

termine the Weibull line with maximum and minimum

slope still compatible with the conﬁdence bounds (com-

pare Fig. 16.106) and then determine β

max

, β

min

, η

max

min

directly. Another possible method is to directly

calculate these parameters as described in [16.103,119].

Three-Parameter Weibull Analysis

There is an additional form of the Weibull distribution

containing a third parameter, the so-called failure-free

time t

. In the three-parameter form, the Weibull failure

function and density function read

F(t) =1− e

−



t−t

η−t



, (16.54)

f (t) =

η −t



t −t

η −t



β−1

−



t−t

η−t



. (16.55)

The failure-free time t

is a parameter that, in the case

β>1, serves to properly describe an incubation pe-

riod, often observed in degradation experiments. Before

no failure is observed. This behavior cannot be de-

scribed with the same accuracy using the two-parameter

Weibull distribution. This becomes necessary if the reli-

ability of complex systems must be calculated from the

reliability functions of the single components the sys-

tem is made of. In [16.121] four criterions are given

when the introduction of t

is indicated.

•

There must be 20 or more failures,

•

The physics of failure shall support the existence

failure-free time,

•

The two-parameter weibull plot shows curvature,

•

The distribution analysis must favor the three-para-

meter form meaning that the correlation coefﬁcient

becomes larger when trying several t

=0.

The failure-free time can be estimated by means of

graphical methods from the Weibull plot. A simple and

commonly used method is introduced by Dubey which

described in detail in [16.103, 122]. So far, the the-

oretical justiﬁcation and the method to determine the

failure-free time was discussed. In Sect. 16.7.5, where

system reliability issues are discussed, the relevance of

the failure-free time t

to practical problems will be

illustrated in more detail.

16.7.3 Reliability Test Strategies

So far, we have assumed that the failure data are already

available and that all tested items have failed within

the observation period. In this section, we will intro-

duce several methodologies for how the data are created

either in practical reliability tests in the lab or from

warranty data.

In practice we always have the constraint that the

sample size as well as the testing time is limited, or

that the data set obtained from a warranty analysis is

incomplete.

Censored Tests

A censored test is a test where either not all items fail or

where not all failures are taken into account for anal-

ysis. Censoring becomes necessary for the following

reasons [16.108].

•

Some failure modes that occur are different from

those anticipated and such units are withdrawn from

the test;

•

We need to make an analysis of the available results

before test completion (time constraints);

•

A warranty analysis is to be made of all units in

the ﬁeld (nonfailed and failed units). The nonfailed

units are considered to be suspended items.

Different types of censoring may occur in practice. Here

we will restrict the discussion to the most important.

Other types of data are presented in [16.123].

Figure 16.107 shows the following cases.

•

a) Some items fail within the observation time (

some survive (→).

•

b) Some items fail (

), and some are removed from

the test (

). We call these suspended items. A pos-

sible reason for suspension is that these items failed

due to another failure mechanism than the one of

interest.

•

c) No item fails. This special case will be dealt with

below.

In the following, we discuss how the data are analyzed

in the given cases.

Case (a): Some Items Fail Within the Observa-

tion Time, Some Survive. In this case, the Weibull

analysis is performed as described for complete tests

in Sect. 16.7.2. Care must be taken that the n used here

is the number of all items, that means, the failures and

the survivors (in our example in Fig. 16.107, this means

n = 6 and not n = 3).

This test has special practical meaning since ﬁeld

data are often of this type: a batch of devices has

been delivered to customers. After a certain time, some

failures are documented, and the rest of the items

Part D 16.7

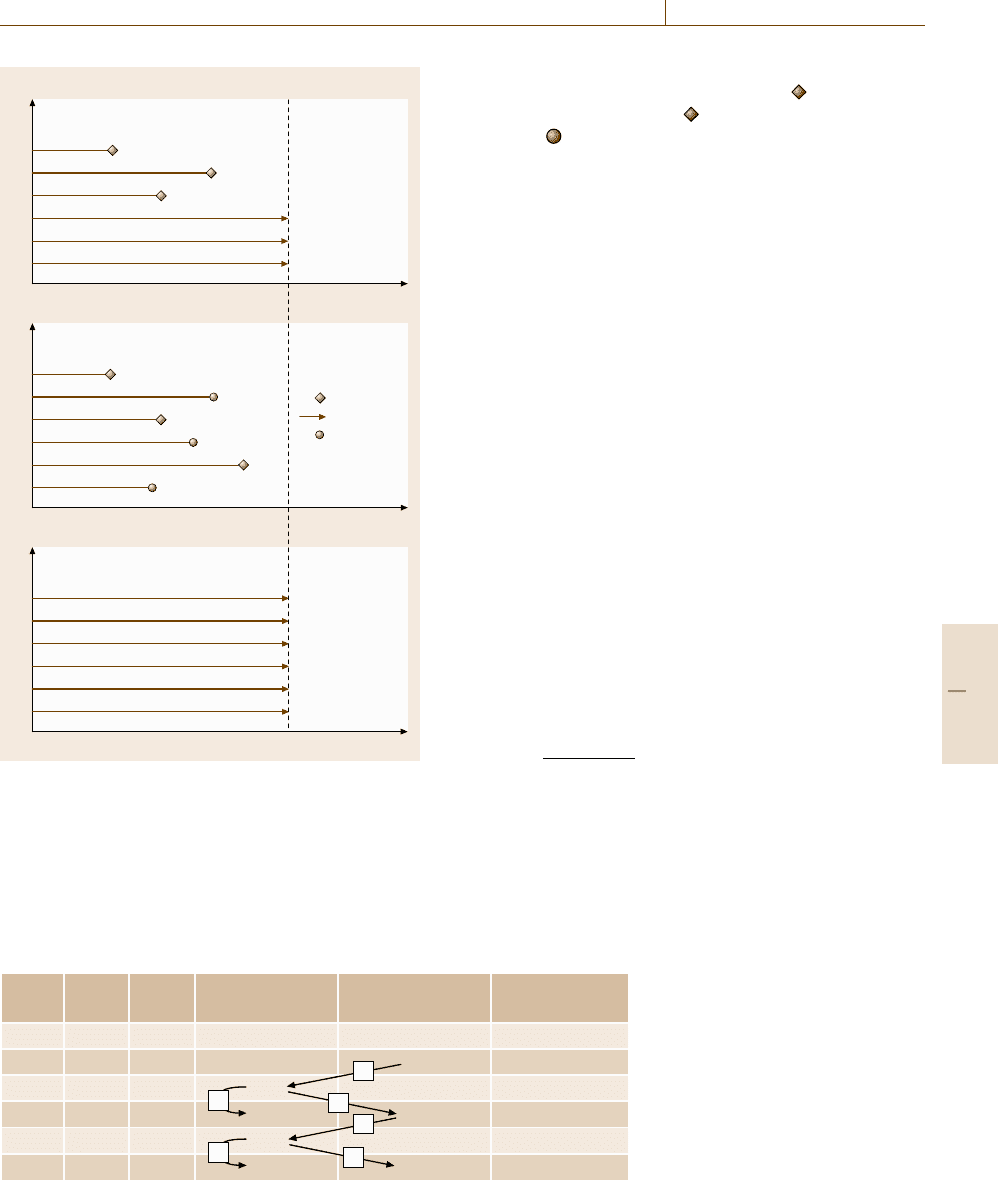
Performance Control 16.7 Characterization of Reliability 957

n =6

Time

n =6

Time

Failure

Survivor

Suspended

n =6

TimeObservation time

is still in function. Those data can be analyzed as

described.

Case (b): Some Items Fail, and Some Are Re-

moved from the Test. The Weibull analysis of

those data requires a technique that differs slightly

from that presented above. In particular, the rank

Item #

Lifetime

Event

F/S

Increment (4.14)

Rank position (4.13)

Median rank (4.1)

0.109

2 L

F 1 2 0.263

3 L

S 1.25 - -

4 L

F 1.25 3.25 0.461

5 L

S 1.875 - -

n = 6 L

F 1.875 5.125 0.754

Table 16.11 Calculation of

the adjusted rank positions

if censored items are present

(for this example, n = 6). By

the arrows it is shown how

the rank positions of failures

following a suspension are

calculated

Fig. 16.107a–c Different events during a reliability tests

during the testing period: (a) Some items fail (

), some

survive (→). (b) Some items fail (

), others are suspended

from the test (

). (c) All items pass the test (Sect. 16.7.3)



positions i must be adjusted because assigning the

usual positions i = 1 −n to each item, regardless of

whether it is neglected in the analysis or not, is

not appropriate. Instead, the procedure is the follow-

ing [16.103]:

•

Step 1: Collect data as usual, and assign it a capital

F(= failed) or S (=suspended), and list the data in

a table in ascending order (Table 16.11).

•

Step 2: Calculate the rank positions for the failed

items, and add them to the table. Suspended data

are neglected. The new rank positions for the

failed items are calculated using the following

rule [16.124, 125]. This is necessary, because a sus-

pended item causes an uncertainty at which rank

position the suspended and the following item are

located. We therefore need to calculate a mean rank

position, which is no longer necessarily a natural

number.

The rank of the j-th item i

is calculated as the sum

of the previous rank i

j−1

and an increment y

j−1

(16.56)

with the increment y

being

n +1 −i

j−1

1 +n

> j

(16.57)

with n being the overall (not only the failed) sample

size, and n

> j

being the remaining number of items

with index being greater than the actual j.

•

Step 3: Calculate the median ranks according

to (16.57) and add them to the table.

•

Step 4: Perform a Weibull analysis as described in

Sect. 16.7.2.

Part D 16.7