Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing

Подождите немного. Документ загружается.

958 Part D Materials Performance Testing

i, min

(%)

Lifetime ratio t

test

dem

100

n =2

n =3

n =5

n =7

n =1

n =10

21.510.5 2.5

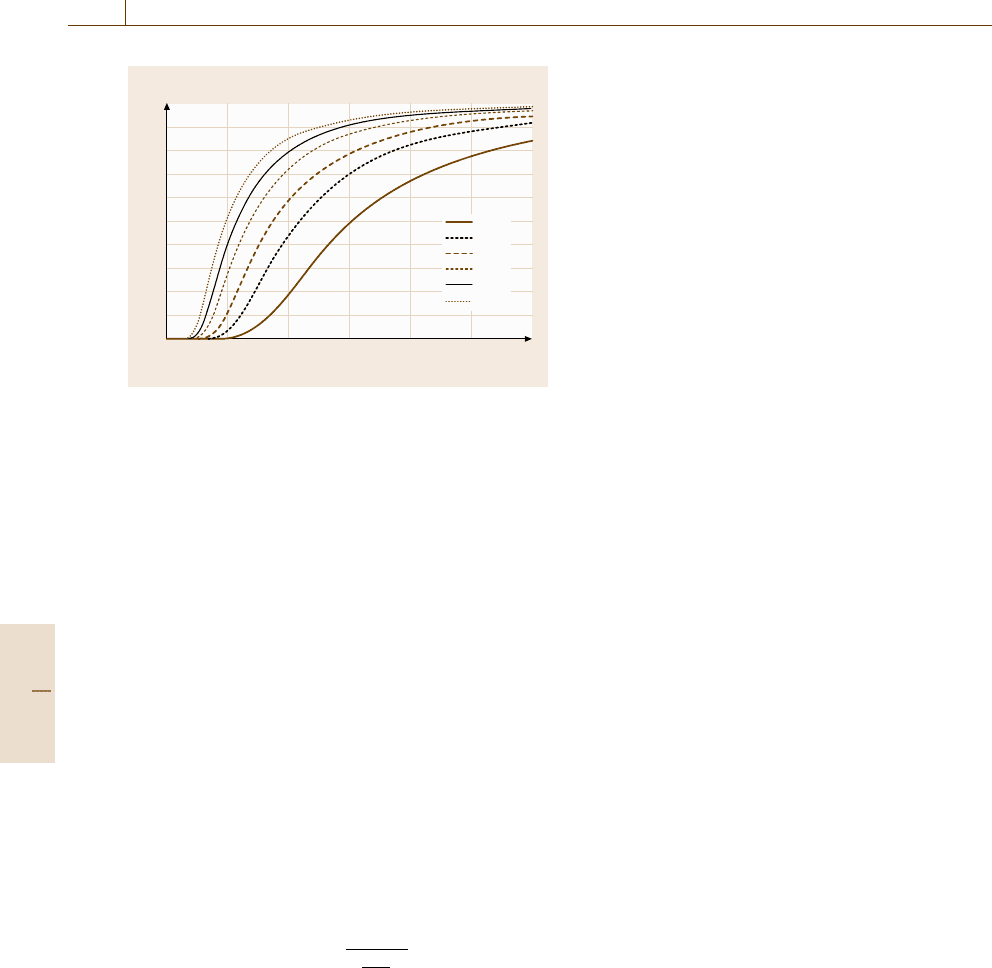
Fig. 16.108 Guaranteed least reliability R

i,min

of a device

tested in a success run as a function of the lifetime ratio

and of the number of samples n. The ﬁgure indicates that

with smaller sample number the testing time must increase

in order to maintain the same reliability level. It is helpful

in practice to know the rule of thumb that a reliability of

90% can be guaranteed when three test specimen survive

2–2.5× the demanded lifetime

Case (c) All Items Still in Function – Success Run. The

success run has become one of the major tools in re-

liability engineering. This is because it combines the

number of test specimen and the testing time. Addi-

tionally, the meaning of the conﬁdence interval α for

reliability estimation becomes most obvious in this kind

of test.

The typical task is the following. We have to guaran-

tee a minimum reliability R

i,min

foradeviceatagiven

demanded lifetime L

dem

. To do so, we have a limited

number of specimens (e.g. n = 3) which we test for

a time t

test

If we assume the basic population to be Weibull dis-

tributed, then the formula for this test reads as follows:

i,min

dem

) =(1−α)

⎡

⎢

⎣



test

dem



⎤

⎥

⎦

. (16.58)

For the derivation of this expression see [16.105]. It’s

meaning is that, if n components survive a reliabil-

ity test of duration t

test

> L

dem

, then we can guarantee

a minimum reliability R

i,min

of the device at the de-

manded lifetime L

dem

at a conﬁdence level of α.

In practice, it is often the case that a conﬁdence

level as well as the least guaranteed reliability at

the demanded lifetime are given. From (16.56), we

can calculate the necessary number of specimen and

the corresponding testing time which is necessary to

conﬁrm that the given reliability can be guaranteed.

This important result is seen in Fig. 16.108 where the

least guaranteed reliability is plotted as a function of

the so-called lifetime ratio t

test

dem

and the sample

number.

The main drawback of the test is that the Weibull

parameter β must be known in advance. It cannot be

determined using this method. It must be known from

experience, similar studies or from tests under simpli-

ﬁed conditions.

Degradation Tests

Degradation testing is a rather new method that has re-

cently attracted many researchers [16.126, 127]. This

kind of testing is possible if there is a parameter that

can be measured during the operating time of the de-

vice and which indicates the degradation process. The

plotting of the parameter versus the lifetime describes

the so-called degradation path. As an example, the abra-

sion of a car tyre can be measured during a test and

plotted versus the driven kilometers. From the data

points we can extrapolate to longer lifetimes and es-

timate the time when the abrasion reaches a critical

value. The extrapolation data from n devices tested re-

sult in n lifetimes that can be analyzed with Weibull

as described before. The beneﬁt is that the test can be

truncated at a time much smaller than the expected life-

time. Some research is ongoing on how long a device

must be tested until the extrapolation becomes good

enough [16.128].

Example. A ferroelectric memory chip can distinguish

between logic 1 and 0 if the polarization states P(N)

after N polarization reversals (cycles) do not fall be-

yond 80% of the initial value P

. P(N)/P

= 80%

is therefore the failure criterion of the device. Let

us assume a cycling test with four samples was car-

ried out, where P(N) is measured after a discrete

number of cycles. In order to save time, the mea-

surements are truncated after 10

cycles, although

the failure criterion is not reached. From the liter-

ature, it is known that P(N) is related to N by

P(N)/P

= exp(−N/N

∗

) +C, where N

∗

and C are

constants [16.129]. This model can be ﬁtted to the data

points and extrapolated to higher cycle numbers than

in order to ﬁnd the lifetimes L

where the fail-

ure criterion is fulﬁlled (Fig. 16.109). With L

given,

a Weibull analysis may be performed as already de-

scribed in Sect. 16.7.2.

Part D 16.7

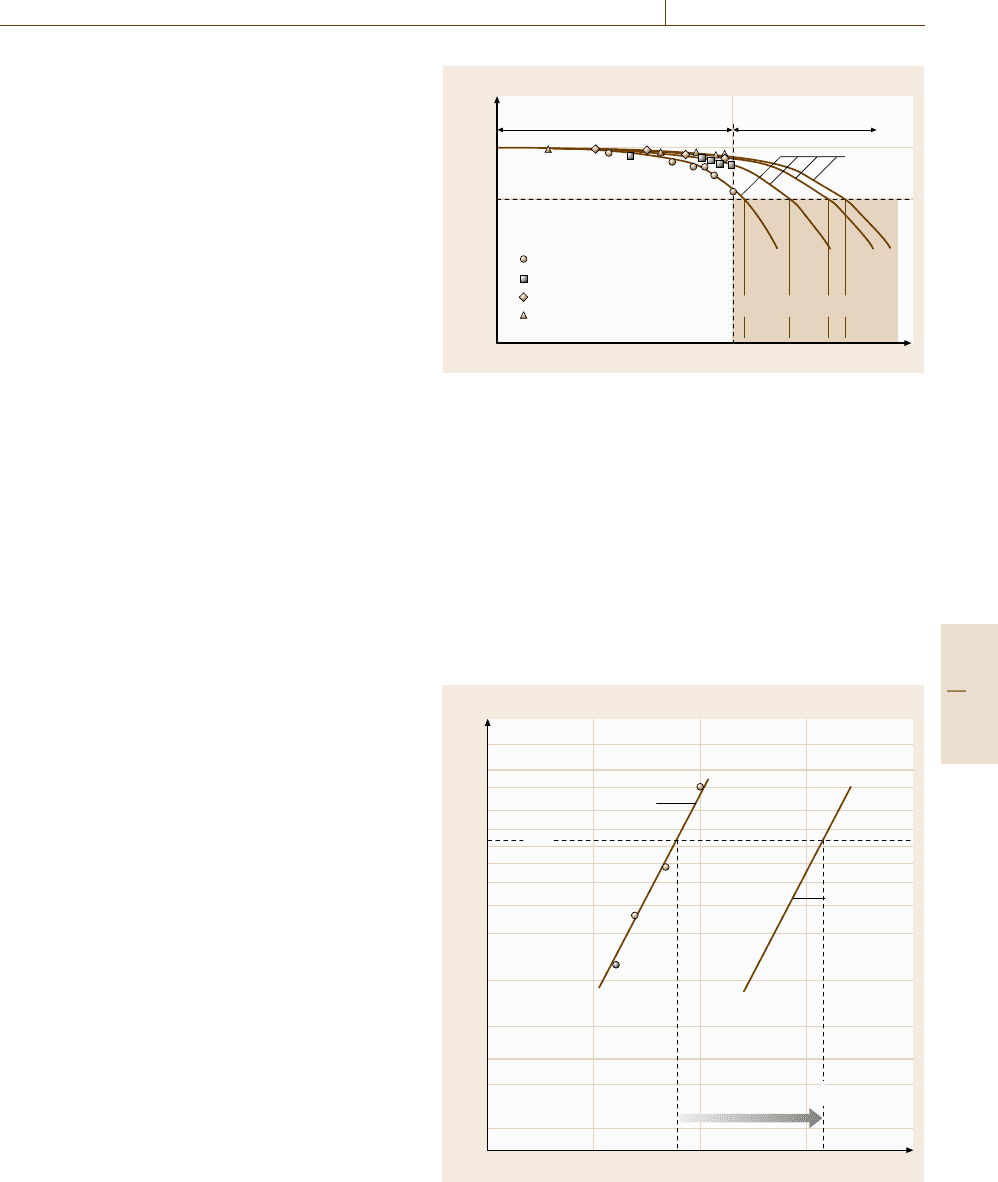
Performance Control 16.7 Characterization of Reliability 959

Fig. 16.109 Degradation test. Four devices were tested and

the data were extrapolated to the critical failure value of

80% remaining polarization. The lifetime data can now be

analyzed by means of the Weibull analysis 

16.7.4 Accelerated Lifetime Testing

Accelerated lifetime testing (ALT) is a frequently used

method for reducing test time. Many publications deal

with the special problems arising from this proce-

dure [16.130].

The basic idea of an accelerated lifetime test is

to apply higher stresses to the device than it experi-

ences under real service conditions in order to provoke

a reasonable number of failures within a reasonable

time. Here, stress means any physical process that

inﬂuences the lifetime of the device; it may be me-

chanical stress, electrical voltage, current, temperature,

humidity and so on. New questions arise from this

procedure.

•

By what factor do the higher stresses accelerate the

degradation process? How are higher stresses and

shortened lifetime physically related?

•

In how far do higher stresses inﬂuence the failure

mode? Will higher stresses produce failure modes

that would not have occurred under normal condi-

tions?

In ALT it must be assured that the observed failures at

higher loading originate from the same failure mech-

anism that would be expected under use conditions in

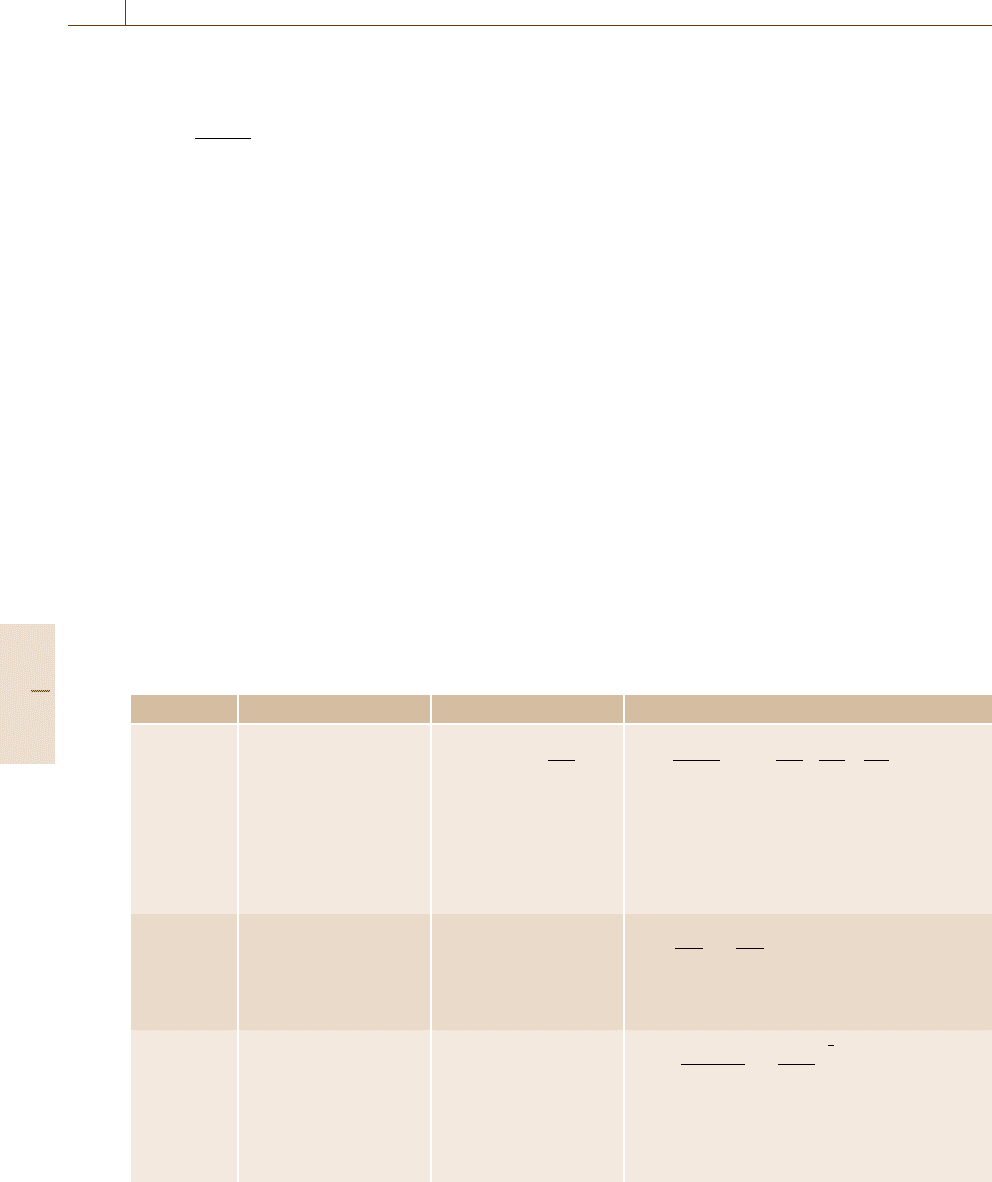
practise. A proof for this is the following rule.

•

Failures that origin from the same failure mecha-

nism show the same shape parameter in the Weibull

net, and therefore are shifted parallel to each other.

They only differ in their lifetime, which is shorter

for higher stresses (Fig. 16.110).

•

Only the lifetime L of the device, which may be

expressed by any parameter related to the dis-

tribution (MTTF, η, B

, ...) is affected by the

acceleration.

Fig. 16.110 The Weibull line obtained from measurements

at higher stress is transferred to the Weibull line that would

have been achieved from experiments at use stresses by

multiplying the lifetime (here the characteristic life) by an

acceleration factor κ. The Weibull parameter β is assumed

to remain constant if the failure mode is the same at both

stress levels



P(N)/P

100 %

80 %

Cycles, log N

Measured Extrapolated

Failure criterion

Model

equation

Device 2

Device 3

Device 1

Device 4

Analysis Procedure

The acceleration is measured by the ratio by which the

lifetime is shortened by applying a higher stress. This

number is called the acceleration factor.

Let us assume that we can calculate the time to fail-

ure L from a model equation L(S), where S is the stress

level applied to the item. L(S) is the functional de-

scription of the dependency of the lifetime on the given

physical quantity.

Now let us assume that we test the device at two dif-

ferent stress levels with S

acc

> S

use

. (where “acc” stands

for acceleration, and “use” means the normal use con-

Failure probability F(t) (%)

99.9

63.2

use

= κη

acc

Lifetime (log)

use

= β

acc

Projection to

low stresses

(use)

Data measured

at high stresses

(acc.)

Part D 16.7

960 Part D Materials Performance Testing

dition of the device) Then we deﬁne the acceleration

factor κ as follows

κ =

L(S

use

)

L(S

acc

)

. (16.59)

The basic rule for how an accelerated reliability

test is to be performed can be summarized as follows

(Fig. 16.110).

•

Step 1: Collect failure data at higher stresses S

acc

•

Step 2: Perform a Weibull analysis as described in

Sect. 16.7.2.

•

Step 3: Calculate the lifetime at normal use condi-

tions by applying a suitable physical model describ-

ing the acceleration. Those acceleration models are

described below.

Acceleration Models

Using acceleration models, the mechanistic origin of the

acceleration is described. For any accelerated lifetime

testing, this is a crucial point at which the validity of the

whole test is decided. Two basic problems arise at this

point

•

In most cases, the physical model must be known

from preknowledge on the physical origin of the ob-

Table 16.12 Commonly used acceleration models, with their applications, model equations and acceleration factors.

These and further models can be found in [16.109]

Model Application Model equation Acceleration factor

Arrhenius Failure mechanisms that

depend on chemical

reactions, diffusion

processes or migration

processes. It covers many

of the nonmechanical

(or nonmaterial fatigue)

failure modes that cause

electronic equipment

failure

L(T ) = A exp



ΔH



T: temperature (K)

A: constant

: Boltzmann constant

ΔH: activation energy

of the process (must be

known in advance)

L(T

use

)

L(T

acc

)

=exp



ΔH



use

−

acc



Inverse

power law

(IPL)

Stresses which are non-

thermal in nature; in most

cases the stress is given to

be electrical voltage, e.g.,

capacitors often follow the

IPL relationship

L(U) = AU

−b

U: driving voltage of the

device

A: constant

b: characteristic exponent

use

acc



acc

use



Cofﬁn–

Manson

Mechanical failure, ma-

terial fatigue or material

deformation, crack growth

in solder and other metals

due to repeated tempera-

ture cycling as equipment

is turned on and off

Δε

= A

Δε

: plastic strain ampli-

tude (peak–peak)

: number of cycles to

fail

c: cycling exponent (must

be known in advance)

A: material constant

Δε

(Δε

use

)

(Δε

acc

)



Δε

acc

Δε

use



served failure. It is not sufﬁcient to adjust model

equations to the given failure data.

•

Physical models contain parameters (such as the ac-

tivation energy, for instance; see below) that have to

be estimated or known from the literature. In a few

cases only these parameters can be calculated from

the failure data directly.

In the following Table 16.12, some of the common ac-

celeration test models are discussed in order to show

the principle. Here, we restrict the discussion to the

Arrhenius, the inverse power law (IPL) and the Cofﬁn–

Manson model.

Advanced Acceleration Techniques

In recent years, some acceleration methods have arisen

that differ markedly from the scheme above sketched.

In particular, the highly accelerated lifetime testing

(HALT) and highly accelerated stress screening (HASS)

methods have gained increasing attraction in the near

past.

The goal of these methods is to ﬁnd weaknesses

of a product at an early stage of development, e.g. for

a prototype, rather than predicting the lifetime of the

device.

Part D 16.7

Performance Control 16.7 Characterization of Reliability 961

We will mention these methods in brief here, and

recommend the papers referred to in [16.131] for further

information on this topic.

Step Stress Proﬁle Testing. In this test, test specimens

are ﬁrst subjected to a given level of stress for a certain

period of time, and are then subjected to a higher level

of stress. The process continues at increasing levels of

stress, until either all the specimens fail, or the time pe-

riod at the maximum stress level ends. The advantage

of this method is, that failure modes are provoked, how-

ever, with this technique it is very difﬁcult to model the

acceleration properly [16.131].

It is mainly used for deﬁning the operating envelope

of a product and as a possibility to compare variants in

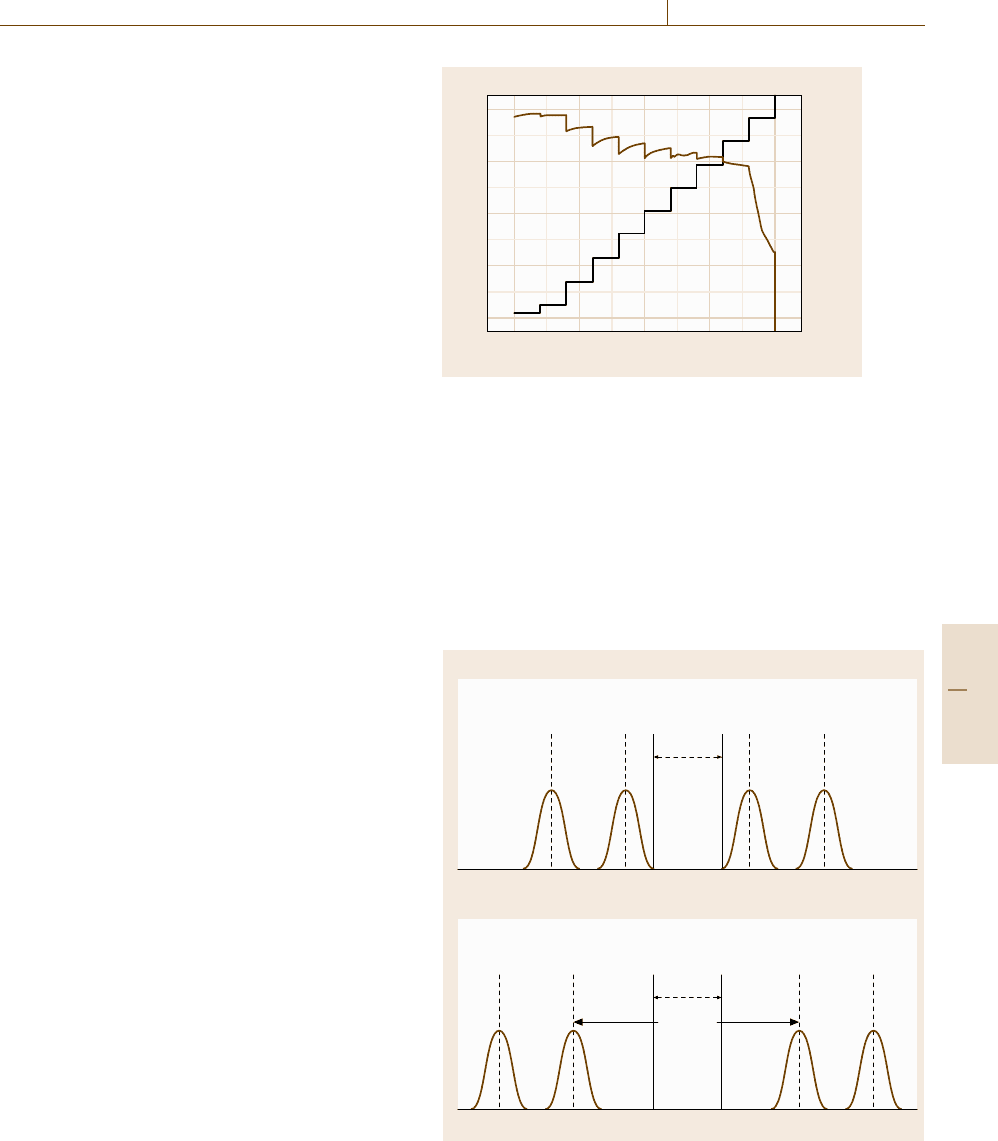
a short period of time. An example for a step stress of

a semiconductor transistor (in this case a high-electron

mobility transistor) is shown in Fig. 16.111 [16.132].

In this case the drain voltage (black line) of the tran-

sistor is increased stepwise nearly every 100 min until

80 V. At ≈60 V the gate current (brown line) excess

100 μA rapidly leading to a catastrophic degradation of

the device.

HALT (Highly Accelerated Lifetime Testing). HALT is

an development test with the intention to detect weak

spots in a system within a short time using a small

number of samples.

The main motivation of HALT is not the survival of

the product under speciﬁed conditions but to provoke

the product/system to fail and detect dormant defects

and provide the opportunity to improve reliability of the

product. This method should be performed at the begin-

ning of a product development as soon as a prototype

is available so that redesign efforts are still affordable.

A generalised illustration of the goal behind using HALT

is shown in Fig. 16.112 [16.133]. The upper part shows

the limits of a prototype before performing HALT. The

abscissa represents the stress (vibration, temperature,

voltage, etc.) the specimen is subjected to. The black

continuous lines indicate the operational area deﬁned

by the product speciﬁcations. The inner dotted lines

represent its operational limits, at which the device re-

mains in a state of operation and at which any further

increase in stress will cause a recoverable failure. The

outer dotted lines represent the destruction limits, mean-

ing that a stress exceeding these limits will destroy the

device. By subjecting the specimen to increasing stress

levels of temperature and vibration (independently and

in combination) and other stresses speciﬁcally related to

the product beyond operating conditions, it is possible

Gate current (μA) Drain voltage (V)

Time (h)

20151050

100

200

300

400

Fig. 16.111 On-Wafer Step-Stress-Tests until catastrophic

degradation of a semiconductor transistor. The drain volt-

age (black line) of the transistor is increased stepwise nearly

every 100 min until 80 V. At ≈60 V the insulating fails and

thegatecurrent(brown line) excess 100 μA rapidly leading

to a catastrophic degradation of the device (after [16.132])

to determine the above-mentioned functional operating

and destructions limits, multiple failure modes and root

causes. Based on the obtained results improvements of

Lower

destruct

limit

Lower

oper.

limit

Upper

oper.

limit

Product

operational

specs

Operating

margin

After HALT

Stress

Upper

destruct

limit

Lower

destruct

limit

Lower

oper.

limit

Upper

oper.

limit

Product

operational

specs

Prior to HALT

Stress

Upper

destruct

limit

Fig. 16.112 An illustration of the enhanced operating limits due to

HALT (after [16.133])

Part D 16.7

962 Part D Materials Performance Testing

Vibration (g rms) Temperature (°C)

Time (min)

1007550250

–10

–50

150

100

200

–100

Vibration (g rms) Temperature (°C)

Time (min)

806040200

–10

Temperature (°C)

Time (min)

806040200

–25

100

–50

Temperature (°C)

Time (min)

200150100500

100

–50

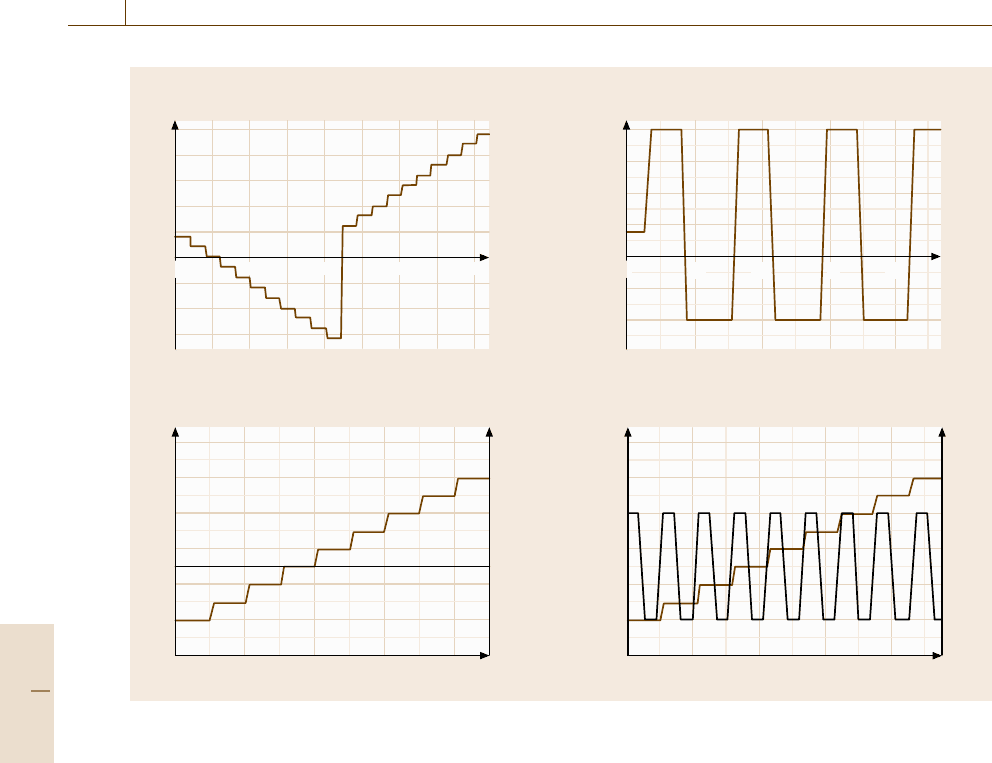
Fig. 16.113a–d An exemplary overview of possible tests including temperature and vibration loads

the prototype are carried out, leading to a higher ro-

bustness of the prototype shown in the lower part of

Fig. 16.112. The prototype shows an increased opera-

tional area and the operation and destruction limits are

shifted to higher levels.

Figure 16.113 shows an exemplary overview of dif-

ferent tests, which can be used for HALT. Graph a

shows a temperature test, in which the temperature is de-

creased and later increased stepwise overthe time. Graph

b shows rapid thermal transitions causing rapid expan-

sion and contraction of the prototype. Graph c illustrates

a test, in which the acceleration levels of the random vi-

bration are increased at a constant temperature. In the

last graph d two loads are combined, in this case increas-

ing vibration levels and rapid thermal transitions.

The obtained results can also be used later for HASS

(see below). Complaints with HALT are the inability of

reproducing failure modes because of the random nature

of HALT tests and the inability to predict the reliability

based on statistical data.

HASS (Highly Accelerated Stress Screening). HASS

is a form of accelerated environmental stress screening

and it is used for screening in the production process de-

tecting weak products and changes in the manufacturing

process. Samples of product assemblies are exposed to

all stresses simultaneously for a very limited time pe-

riod. The level of stresses can exceed beyond operating

limits and near destruct limits obtained by HALT before-

hand. These levels were predeﬁned in a process called

Proof-of-screen (POS) with the goal that HASS detects

relevant defects without removing too much life from the

test items. By passing HASS successfully, it is possible

to ensure that a product has passed its infancy (see bath-

tub curve region 1) before being delivered to a customer.

These and further information can be found in [16.134].

16.7.5 System Reliability

In many practical cases, a system is manufactured from

several single components. The reliability R

of the

Part D 16.7

Performance Control 16.7 Characterization of Reliability 963

whole system depends on the reliability of the single

components R

Serial Systems

In practice, it is often the case that the system’s func-

tionality depends on the component functionality such

that a failure of any component means a failure of the

whole device. For example, the system reliability of

a car depends on the reliability of the tyre as well as

on the engine. From this example, we see that the com-

ponents do not necessarily need to interact with each

other directly.

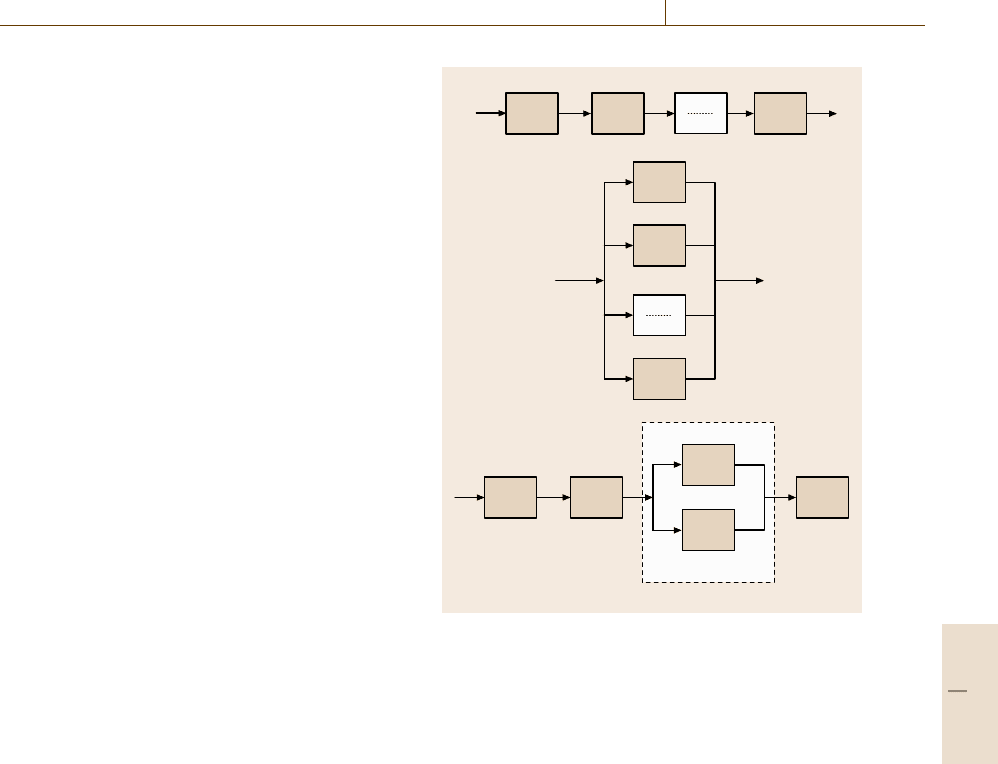
The underlying system structure can be inter-

preted as a serial system structure, which is shown in

Fig. 16.114a.

For a serial system, the reliability of the system at

a given time t is calculated to be the product of the re-

liabilities of the components, what follows from basic

rules for probability calculations:

S,serial

(t) = R

...R



(t) (16.60)

or, by using F

=1−R

and F

=1−R

S,serial

(t) =1−



[1−F

(t)]. (16.61)

From these relations, we can draw some important con-

clusions

•

the more components with given reliabilities, the

smaller the system reliability becomes;

•

in order to maintain a high reliability of the system,

the reliability of the components must be improved;

•

the system cannot be better than the worst compo-

nent.

The reliabilities of the components as well as the sys-

tem reliability can be visualized in a Weibull plot.

In Fig. 16.115 we see this for the case of a three-

component system. The thick line represents the

Weibull distribution of the whole system as a result of

the multiplication rule introduced above.

From this plot, we ﬁnd further interesting facts.

•

The system Weibull line is always located towards

lower lifetimes. (This is identical to the above state-

ment that the system has a lower reliability than the

components.)

•

Due to the sensitivity of the system reliability to

the component reliability, it makes a signiﬁcant

difference if we use the two- or three-parameter

Parallel subsystem

Fig. 16.114 (a) Serial system; (b) parallel system; (c) com-

bined system

Weibull distribution for the components. If the

two-parameter distribution is used although a three-

parameter distribution is justiﬁed, then the failure

probability is overestimated. This leads to an

over-dimensioning of the device. Especially in me-

chanical engineering, where the strength of a device

is dependent on the material amount, this plays an

important role from an economical and ecological

point of view [16.135].

Parallel Systems, Redundancy

If the system contains components that are able to ful-

ﬁl the same functionality as other components, then the

system contains redundancy. In the system structure,

those components are represented as parallel structures,

asshowninFig.16.114b.

In contrast to a serial system, additional redundant

components increase the reliability. This is also indi-

cated in the system equations for parallel systems where

the failure probabilities F(t), rather than the reliabili-

ties, are multiplied

S,parallel

(t) = F

...F



(t) (16.62)

Part D 16.7

964 Part D Materials Performance Testing

Failure probability F(t) (%)

99.9

63.2

Lifetime (log)

ABC

System

Components

Fig. 16.115 The reliability of a system as a result of the reliabili-

ties of its components, here for the example n = 3 and for a serial

system. We see that the system reliability is always lower than the

reliability of the weakest part. In this example, the system reliability

is dominated either by component C or A, depending on the region

of the failure probability. Component B, on the other hand, has mi-

nor inﬂuence since it is more reliable than the others in the whole

region

or, expressed in terms of the reliability functions R

(t) =

1 −F

(t)

S,parallel

(t) =1 −[(1 −R

)(1 −R

) ...(1 −R

)]

=1 −



[1 −R

(t)]. (16.63)

Combined Systems

In practice, it is often the case that within a system some

components are in series and others are parallel. In this

case, the system reliability can be calculated from the

rules of Boolean algebra. A simple example will eluci-

date the principle.

In Fig. 16.114c we see the functional structure of

a system. The system reliability calculates as follows

= R

[

1 −(1 − R

)(1 −R

)

]



 

=parallel subsystem

. (16.64)

16.7.6 System Reliability Estimation

in Practice

Despite the fact that the theoretical background of

reliability engineering, as illustrated in brief in the

proceeding sections, is well deﬁned, the application

of these tools in practice is far from straightforward.

There are several practical problems of which the fol-

lowing are the most prominent [16.136]: (a) systems

are tending to become more complex. (b) Mechanical,

electronic and software components are simultaneously

included in the functionality of systems, for exam-

ple X-by-wire techniques. Such mechatronic systems

will be one of the future challenges in reliability en-

gineering, which has also been documented by the

increasing number of publications in this ﬁeld over the

last years [16.137].

In the following example, we will elucidate all

these problems by following the procedure in reliabil-

ity estimation as sketched above. We will show that all

above-mentioned problems will be addressed in this ex-

ample, giving a better understanding of the underlying

methodology. The example chosen here was subject of

a detailed reliability investigation performed by the au-

thors. We will refer to a previous publication [16.138]

where this work is already described in detail. The

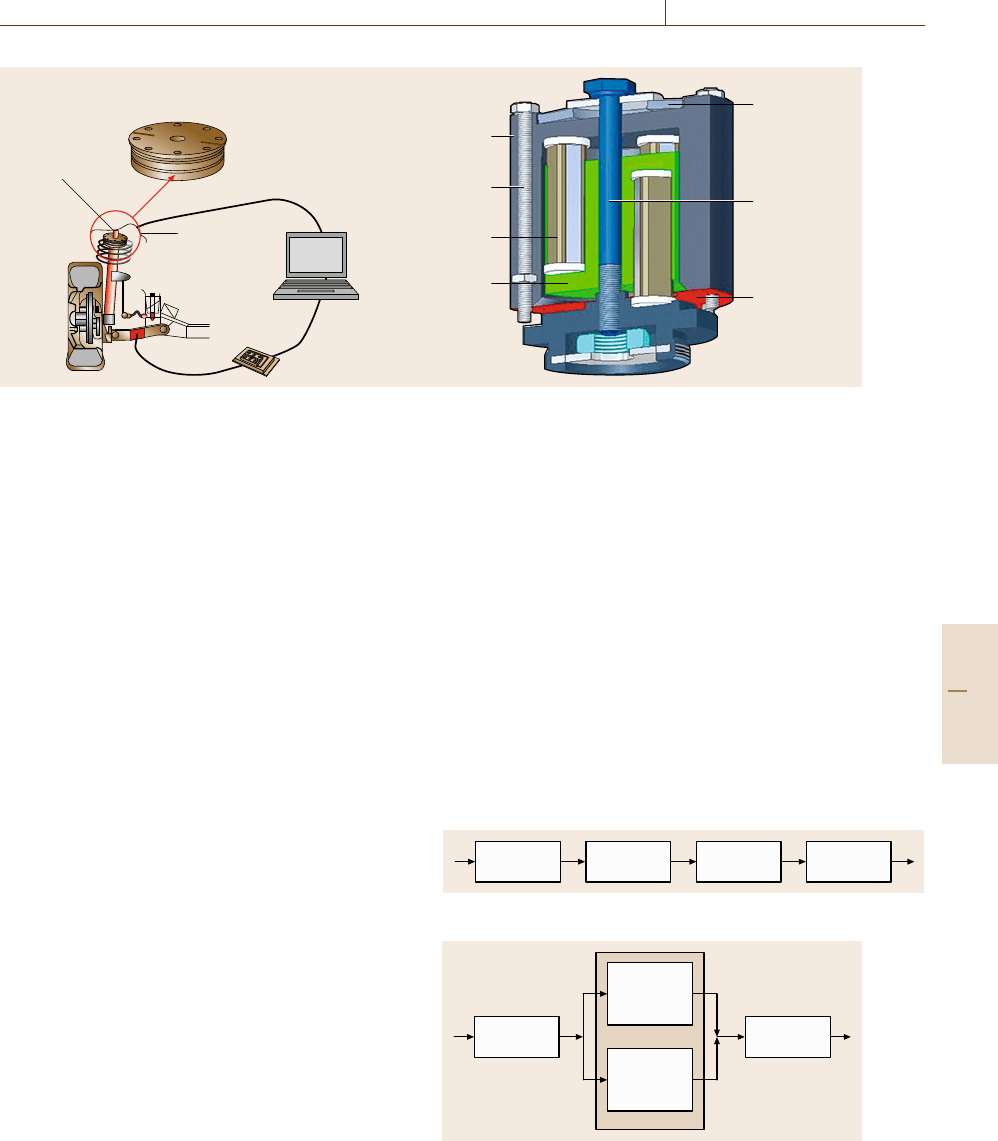
system to be investigated in our example is an active in-

terface (AI), which was designed for actively damping

unwanted vibrations as well as noise in an automobile,

Fig. 16.116 [16.139].

According to the above sketched procedure, the reli-

ability analysis was conducted following this sequence

of steps: i) System analysis, ii) Determination of com-

ponent reliabilities, iii) Determination of the system

reliability.

i) System Analysis

As already described above, the aim is to ﬁnd the un-

derlying abstraction of the system structure according

to Fig. 16.114, which will be the basis for the later sys-

tem reliability calculation. To do so, the system was

subdivided into the following main subsystems.

•

Mechanics,

•

Electronics,

•

Actuators,

•

Control.

From a function analysis performed by the experts in

the ﬁeld of the different technical domains, it became

clear that a failure of one of these subsystems will result

in a system failure. Furthermore, the analysis revealed

Part D 16.7

Performance Control 16.7 Characterization of Reliability 965

Housing

Active

interface

Prototype of the

active 3 DOF interface

Sensors for

vibration

detection

Housing

cascades

Tension spring

Tension screw

Thrust relief

Housing screw

Piezoelectric

actuator

a) b)

Fig. 16.116 (a) The active interface is located within the spring dome of a car. Sensors detect the unwanted vibrations,

the signals are transferred to a controller and a power unit, which drives the piezoelectric actuators acting against the

vibrations. (b) Inner construction of the active interface

that the failure behaviour in each subsystem is in large

parts independent of the failure behaviour of the others.

It must be stated that the determination of this indepen-

dence is by far not trivial, since in many practical cases

not all possible failure modes are known in advance. In

our case, a thorough failure mode and effects analysis

(FMEA) was performed prior to the reliability inves-

tigation, and so a broad knowledge on possible failure

modes was present [16.140]. The system structure of the

active interface is therefore given as a serial structure

showninFig.16.117.

The subsystems themselves were further analysed

in order to determine their reliability structure. For

instance, for parts of the mechanical construction

a combined structure (serial and parallel elements, com-

pare Fig. 16.114c was found as sketched in Fig. 16.118.

ii) Determination of Component Reliabilities

In this section, the determination of the reliabilities of

the aforementioned subsystems mechanics, electronics,

actuators and control will be described. It will be shown

that the underlying method is different in each domain.

Further more, state of the art within the domains also

widely differs. The main problem in daily practice is

that we need failure data of the components for the cal-

culation of system reliabilities following the schemes

sketched above. Those failure data – as we have outlined

in the previous sections – are not sufﬁciently repre-

sented by giving a lifetime of the device. Instead, the

failure behavior in the form of the Weibull parameters,

containing information about the average life and the

scatter, is needed. As already mentioned, these values

are not documented in public data bases. Exceptions

are failure rates for electronic devices and structural

durability data for metallic components [16.114].

Mechanics. The reliability of the construction of the ac-

tive interface is characterized by standard methods of

structural durability. For information and further refer-

ences see [16.114]aswellasChap.7 in this handbook.

Electronics. The determination of the reliability of elec-

tronic components is ﬁxed in international standards.

One of the ﬁrst standards in this ﬁeld was the MIL-

Std 217 [16.141], another newer standard is the IEC

TR 62380 [16.142]. In both cases, a constant failure

Actuators

Electronics

Mechanics

Control

Fig. 16.117 Serial reliability structure of the active interface

R1.3

Bonding

R1.2

Threaded

connection

R1.1

Bias spring

R1.4

Shear relief

Fig. 16.118 Combined reliability structure of a part of the

subsystem mechanics

Part D 16.7

966 Part D Materials Performance Testing

rate for the electronic components is assumed, which

depends on the load conditions (temperature, moisture,

mechanicalvibrations,...).Thereliability of the whole

electronic subsystem is determined by addition of all

failure rates.

Actuators. Additional challenges arise from the fact that

mechatronic systems often include new materials that

serve as actuators or sensors. This class of materials is

called smart materials. These active materials, which

include ferro- and piezoelectric ceramics [16.143, 144]

and shape-memory alloys [16.145], exhibit failures

under long-term operation that are not well under-

stood despite intensive work over the last decades. In

particular, it is not understood which failures occur

under which service conditions (electrical, mechani-

cal stress, temperature, etc.), and the failure probability

functions under those service conditions are not yet

known.

The actuators used in the AI consist of piezoelec-

tric materials. Piezoelectric materials have been used

in the context of adaptronic systems for several years,

however, reliability data available from manufacturers

refer to service conditions from other applications like

fuel injection systems or micro positioning. It is there-

fore a challenging task to transfer the given reliability

data to the actual service conditions of the AI. This can

only be done by combination of expert judgement and

experimental tests where necessary.

Control. The controllers at one hand consist of elec-

tronic hardware, which was already described in the

previous section. On the other hand, it consists of

software components, which differ markedly from hard-

ware components with respect to their failure behavior.

Up to now, there is no general reliability model for soft-

ware available [16.146]. Present methods of software

reliability estimation, as e.g. described in [16.147,148],

are able to quantify implementation failures mainly. Im-

plementation failures origin from human programming

errors [16.149]. State of the art is the assumption of

a correlation between the amount of generated codes

and the amount of failures, which is, on the other hand,

not generally accepted [16.150]. A quantiﬁcation of

speciﬁcation errors is not possible at current state of the

art [16.149].

iii) System Reliability

Based on the information gained from the above de-

scribed procedure, it was possible to estimate the

Weibull parameters characteristic lifetime, Weibull

module and failure free time for the subcomponents

(compare Sect. 16.1.2).

Under the given preassumption, that the failure

behaviors of the subcomponents are independent, the

system reliability function of the AI reads, following

Sect. 16.1.5, as follows

Active interface

= R

mechanics

× R

electronics

× R

actuator

× R

control

. (16.65)

The system reliability function R

is obtained from

multiplication of the component reliability functions ac-

cording to (16.65). In case of time-dependent failure

behavior, the analytical solution of the mutiplication

in these equations can only be solved by computa-

tion. This was done by means of the software package

SYSLEB, which was developed at the IMA (Institute

of Machine Components, University of Stuttgart) for

the purpose of conducting several analyses. SYSLEB

is a powerful software package to analyse life cycle

data using different distributions (e.g. Weibull, normal,

lognormal, exponential). Computation of Weibull dis-

tribution parameters including conﬁdence limits as well

as extensive mathematic and graphic illustrations are

more SYSLEB-features used for this work. Maximum-

Likelihood estimation for combinations of several

distribution functions and Monte-Carlo-simulation are

further possibilities to use SYSLEB for analyzing sys-

tem reliability.

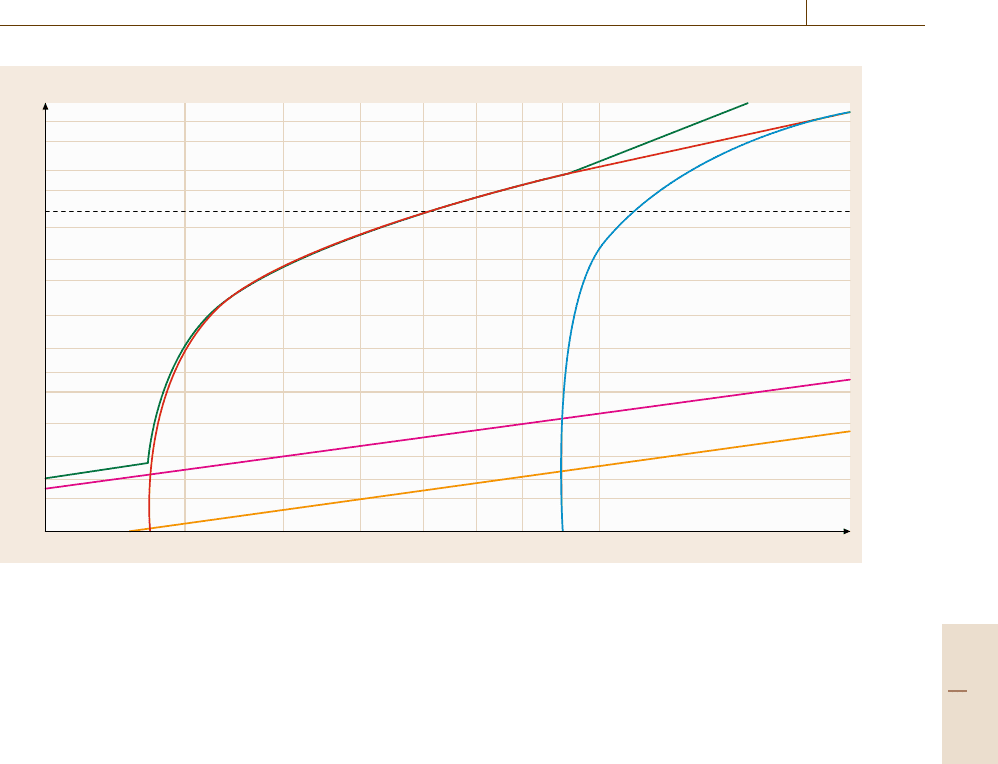
In order to visualize the Weibull lines for the system

reliability function R

(t) as well as for the subcom-

ponents, the Weibull lines are plotted into a Weibull

diagram, what is also a feature of the SYSLEB soft-

ware tool, Fig. 16.119. As can be seen, The Weibull

lines for the components actuator (red), bias spring

(blue), controller (magenta), ampliﬁer (yellow) as well

as the resulting system reliability line (green) are shown

in one graph according to the schematic drawing in

Fig. 16.115.

For the electronic components like controller and

ampliﬁer, a constant failure rate was assumed, what

is typical of electronic components. In the Weibull

plot, this is expressed by a straight line. The other

components were assumed to have a wear-out fail-

ure behavior with a given failure-free time. As can

be seen from the plot, the system reliability curve

at lower lifetimes depends on the failure behavior of

the electronic components. However, after reaching the

failure free time of the actuators, the actuators start

to dominate. Only after very long lifetimes, the bias

spring gives a signiﬁcant contribution to the system

reliability function. As can be seen from the Weibull

Part D 16.7

Performance Control 16.A Appendix 967

Failure probability F(t) (%)

99.9

99.0

90.0

80.0

50.0

30.0

20.0

10.0

5.0

63.2

3.0

2.0

1.0

0.3

0.5

0.2

0.1

Lifetime (t)

Fig. 16.119 Weibull plot of the components actuator (red), bias spring (blue), controller (magenta), ampliﬁer (yellow)as

well as the resulting system reliability line (green) (after [16.138])

plot, an improvement in the reliability of the actu-

ators will have the greatest impact on the system

reliability.

The example shows, how a quantitative reliability

estimation of a complex system can be performed by ap-

plication of the Weibull distribution and Boolean system

theory.

It also shows that there are several preconditions to

be met. On system level the interactions of the com-

ponents must be understood at a depth allowing for

a judgement of the independence of the components,

which is a necessary precondition for the applicability

of the above sketched procedure.

Furthermore, knowledge about the failure behaviour

of the components must be available for the analysis. At

this point, the quality of the available data is most cru-

cial. The general experience is that the data available

do not allow a straightforward introduction to the sys-

tem reliability analysis without prior interpretation of

the available data and without prior expert judgement.

The availability of lifetime data of high quality will

be a main challenge in reliability engineering in the

future.

16.A Appendix

In the following table, the median rank regression for

the 5, 59 and 95% percentiles of the failure probabil-

ity F (in %) are listed for sample sizes from n = 3up

to n = 12. The values are of interest for the Weibull

analysis introduced in Sect. 16.7.2.

Part D 16.A