Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing
Подождите немного. Документ загружается.

1038 Part E Modeling and Simulation Methods
We can derive the following finite difference ap-
proximation on the second derivative of u, ∂
2
u/∂x
2
,
by applying the backward difference scheme at x = x −
h/2 and the forward difference scheme at x = x +h/2
on the first derivative of u, ∂u/∂x
∂
2
u
∂x
2
≈
∂u
∂x
x=x+
h
2
−
∂u
∂x
x=x−
h
2
h
≈
u(x +h) −u(x)
h
−
u(x) −u(x −h)
h
h
=
u(x +h) −2u(x) +u(x −h)
h
2
. (19.19)
Now we can apply the above finite difference approxi-
mations to the given problem in Fig. 19.7
k
∂
2
u
∂x
2
=−f , (19.20)
u(1) =a(u = a at x =1) ,
u
x
(0) =b
∂u
∂x
=b at x =0
. (19.21)
x
u
2
hhh
u
3
u
1
u
0
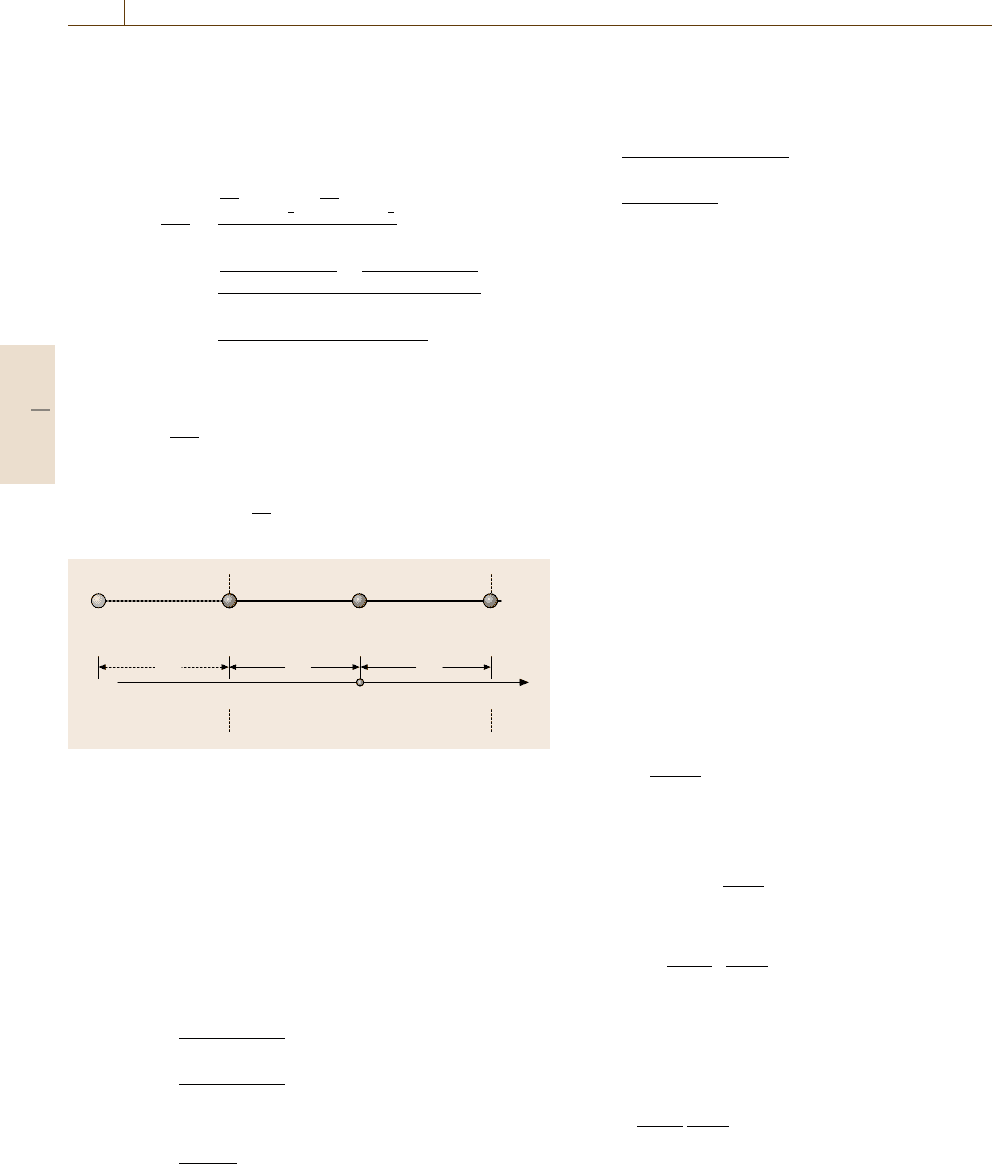
Grid 1 Grid 2
0
123
01
Fig. 19.10 Finite difference grids with a mirror node introduced
Suppose that the domain is discretized into two
grids. Applying the difference scheme for second
derivativestothegoverningequationin(19.20)atthe
non-first-boundary condition-imposed nodes 1 and 2,
we get the system of equations in (19.22). From the
first and second boundary conditions in (19.21), the si-
multaneous equations are obtained as shown in (19.23).
Here node 0 is a mirror node, which is artificially intro-
duced as shown in Fig. 19.8, for the treatment of second
boundary condition.
⎧
⎪
⎨
⎪
⎩
u
2
−2u
1
+u
0
h
2
=−f
u
3
−2u
2
+u
1
h
2
=−f
, (19.22)
⎧
⎨
⎩
u
3
=a
u
2
−u
0
2h
=b
. (19.23)
Equation (19.22) leads to the following solvable sys-
tem of two equations with two variables u
1
and u
2
, after
deleting u
0
and u
3
by using the relationship in (19.23).
⎧
⎪
⎨
⎪
⎩
u
2
−2u
1
+(u
2
−2hb)
h
2
=−f
a −2u
2
+u
1
h
2
=−f
. (19.24)
If a =1, b =0.2, f = 1, h = 0.5, and k = 1, then we
get the following FD-approximated solutions at nodes
1 and 2, which are numerically equivalent to the exact
solutions described at the end of Sect. 19.1, by chance
⎧
⎨
⎩
u
1
=1.300
u
2
=1.275
where a =1, b =0.2, f =1, h = 0.5, and k =1.
Once the values u at all the nodes are obtained, the
derivative values ∂u/∂x can be calculated by applying
finite difference approximations in (19.16–19.18).
19.2.2 Finite Element Method (FEM)
With the same problem setting as in (19.20)and(19.21),
the formulation of FEM is visualized in the following
part.
First of all, we introduce a weight function w,which
is an arbitrary function with zero value at the nodes
of first boundary conditions. Multiplying the governing
equation by the weight function w, and taking the inte-
gral over the domain results in the following equation
1
0
k
∂
2
u(x)
∂x
2
+ f
w(x)dx =0 . (19.25)
Integrating by parts gives
1
0
fw(x)dx +k
∂u(x)
∂x
u(x)w(x)
1
0
−
1
0
∂w(x)
∂x
k
∂u(x)
∂x
dx = 0 . (19.26)
Considering both the first and second boundary con-
ditions in (19.21) and the nature of weight function w
described above we obtain the following
1
0
k
∂w(x)
∂x
∂u(x)
∂x
dx =
1
0
fw(x)dx −kw(0)b .
(19.27)
Part E 19.2
Finite Element and Finite Difference Methods 19.2 Basic Derivations in FEM and FDM 1039
This equation is usually called the weak form. It should
be noted that the second boundary condition is natu-
rally embedded in the weak form during the derivation.
Due to this characteristic, the first and second bound-
ary conditions are called essential and natural boundary
conditions in FEM, respectively.
Up to (19.27), we just used a conceptual deriva-
tion in the continuous exact model without introducing
any approximated discretization. To calculate (19.27)
we introduce some approximated discretized functions
in u and w.
Now we consider the following finite element model
with two linear finite elements.
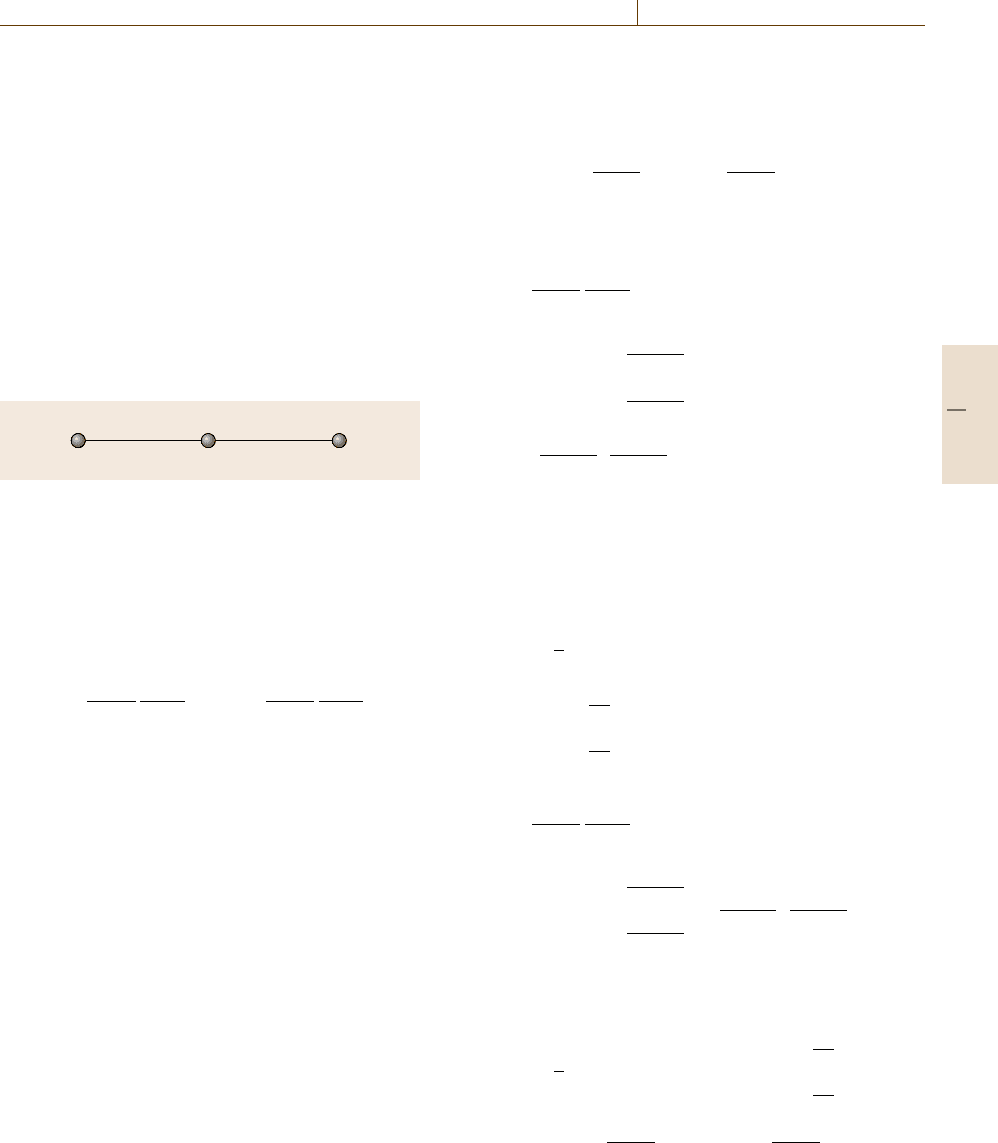
Element 1 Element 2
321
Fig. 19.11 Finite element model
The finite difference method is a scheme with respect
to nodes, while the finite element method is an element-
oriented scheme with element-integral weak form. Thus
(19.27) can be represented as the summation of an
element-wise weak form in FEM as
element#1
k
dw(x)
dx
du(x)
dx
dx +
element#2
k
dw(x)
dx
du(x)
dx
dx
=
element#1
fw(x)dx +
element#2
fw(x)dx −kw(0)b . (19.28)
The linear finite-element-approximated function se-
lected here is represented in Fig. 19.10 and (19.29).
The finite element function can be interpreted as an
interpolation function of the physical values at nodes
1 and 2 in an element by looking at (19.29) carefully.
The upper suffix h in (19.29) represents the element-
wise discretized approximated function.
Since the weight function can be arbitrary with zero
values at the nodes of first boundary conditions, the
same function as the finite element function is applied
in this case.
This setting is usually used in FEM, and is called the
Galerkin (or Bubnov–Galerkin) method. If a different
weight function is selected other than the finite element-
approximated function, we call it the Petrov–Galerkin
method, which is the stabilized upwind case FEM for
fluid dynamics [19.2])
u
h
(x) =u
1
N
1
(x) +u
2
N
2
(x) ,
w
h
(x) =w
1
N
1
(x)+w
2
N
2
(x) ,
where N
1
(x) =
x
2
−x
h
, N
2
(x) =
x −x
1
h
. (19.29)
Matrix manipulation in both elements 1 and 2 are pres-
ented below.
Element 1
element #1
k
dw(x)
dx
du(x)
dx
dx =
element #1
fw(x)dx −kw(0)h ,
element #1
k
w
1
w
2
⎛
⎜
⎝
dN
1
(x)
dx
dN
2
(x)
dx
⎞
⎟
⎠
×
dN
1
(x)
dx
dN
2
(x)
dx
u
1
u
2
dx
=
w
1
w
2
element #1
f
N
1
(x)
N
2
(x)
dx
−k
w
1
w
2
N
1
(0)
N
2
(0)
b ,
w
1
w
2
k
h
1 −1
−11
u
1
u
2
=
w
1
w
2
⎛
⎜
⎝
fh
2
fh
2
⎞
⎟
⎠
−k
w
1
w
2
1
0
b ; (19.30)
Element 2
element #2
k
dw(x)
dx
du(x)
dx
dx =
element #2
fw(x)dx ,
element #2
k
w
1
w
2
⎛
⎜
⎝
dN
1
(x)
dx
dN
2
(x)
dx
⎞
⎟
⎠
dN
1
(x)
dx
dN
2
(x)
dx
×
u
1
u
2
dx =
w
1
w
2
element #2
f
N
1
(x)
N
2
(x)
dx ,
w
1
w
2
k
h
1 −1
−11
u
1
u
2
=
w
1
w
2
⎛
⎜
⎝
fh
2
fh
2
⎞
⎟
⎠
,
where N
1
(x) =
x
2
−x
h
, N
2
(x) =
x −x
1
h
.
(19.31)
Part E 19.2
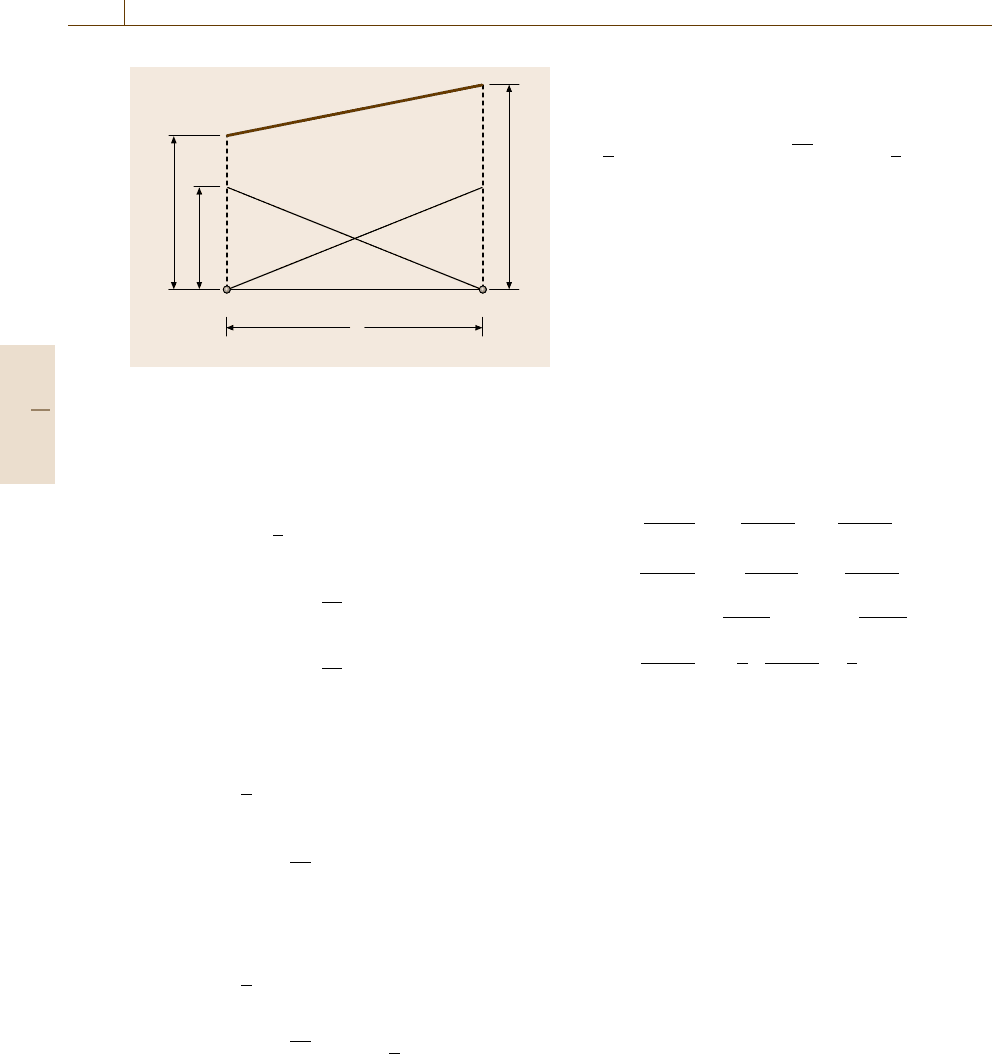
1040 Part E Modeling and Simulation Methods
h
u
1
1
12
u
2
N
2
N
1
x
2
x
1
u
h
= u
1
N
1
+u
2
N
2
Fig. 19.12 Two-node linear-finite-element approximated
function
By combining (19.30)and(19.31) we get the following
total system of equations
w
1
w
2
w
3
k
h
⎛
⎜
⎝
1 −10
−11+1 −1
0 −11
⎞
⎟
⎠
⎛
⎜
⎝
u
1
u
2
u
3
⎞
⎟
⎠
=
w
1
w
2
w
3
⎡
⎢
⎢
⎢
⎣
⎛
⎜
⎜
⎜
⎝
fh
2
fh
fh
2
⎞
⎟
⎟
⎟
⎠
−
⎛
⎜
⎝
kb
0
0
⎞
⎟
⎠
⎤
⎥
⎥
⎥
⎦
. (19.32)
Since w
3
is zero due to the nature of the weight
function,
w
1
w
2
k
h
1 −10
−12−1
⎛
⎜
⎝
u
1
u
2
u
3
⎞
⎟
⎠
=
w
1
w
2
⎡
⎣
⎛
⎝
fh
2
fh
⎞
⎠
−
kb
0
⎤
⎦
. (19.33)
Considering the first boundary condition of u
3
=a,
w
1
w
2
k
h
1 −1
−12
u
1
u
2
=
w
1
w
2
⎡
⎣
⎛
⎝
fh
2
−kb
fh
⎞
⎠
−
k
h
0
−a
⎤
⎦
. (19.34)
Since w
1
and w
2
are arbitrary we can get the follow-
ing solvable system of two equations with two variables
Ku= f in (19.35). It should be noted that the treatment
of the second boundary condition is not needed in the
matrix manipulation part in FEM, which is a different
point from FDM’s case
k
h
1 −1
−12
u
1
u
2
=
⎛
⎝
fh
2
−kb
fh
⎞
⎠
−
k
h
0
−a
.
(19.35)
If a =1, b =0.2, f = 1, h = 0.5, and k =1, then we
get the following FE-approximated solutions at nodes
1 and 2, which are numerically the same as the exact
solutions described at the end of Sect. 19.1, by chance
⎧
⎨
⎩
u
1
=1.300
u
2
=1.275
,
where a =1, b =0.2, f =1, h = 0.5, and k = 1.
In FEM, the derivative values ∂u
h
/∂x are obtained
from the derivative of interpolated function such as in
(19.36)
∂u
h
(x)
∂x
=u
1
∂N
1
(x)
∂x
+u
2
∂N
2
(x)
∂x
,
∂w
h
(x)
∂x
=w
1
∂N
1
(x)
∂x
+w
2
∂N
2
(x)
∂x
,
where N
1
(x) =
x
2
−x
h
, N
2
(x) =
x −x
1
h
,
∂N
1
(x)
∂x
=−
1
h
,
∂N
2
(x)
∂x
=
1
h
. (19.36)
This is all for the basic derivations in FDM and
FEM, but a few important remarks in both FDM and
FEM should be added.
1. The final shape of FDM and FEM calculation is
Ku= f , where K is a sparse matrix, u is a solution
vector and f is a given force vector. K can be sym-
metric or nonsymmetric depending of the physical
problems. K could be nonlinear if K is a function
of u, although K is linear in the problem above.
The treatment of the nonlinear case is discussed in
Sect. 19.8.
2. In this problem setting, both FDM and FEM reached
numerically acceptable solutions compared with
analytical exact solutions. Unfortunately this is just
by chance. Usually both FDM and FEM provide
only approximated solutions and in most cases you
may need careful verification of the obtained numer-
ical solutions, especially in multidimensional cases.
(In the world of FDM and FEM, there exists a big
difference among the one-dimensional case, two-
dimensional case, and three-dimensional case.) This
topic will be treated in Sect. 19.9.
Part E 19.2
Finite Element and Finite Difference Methods 19.3 The Equivalence of FEM and FDM Methods 1041
3. The good news is that both FDM and FEM must be
converged to more accurate solutions if the grid size
or mesh size h is close to zero. To utilize this na-
ture, the convergence test to evaluate the accuracy
is possible in discretized methods, although the ma-
trix size becomes bigger with a tiny grid or mesh
size. It should be noted that the grid (mesh) size
doesn’t have to be uniform. If the accuracy is to
be improved locally, for example, around a singu-
lar point, it is a good idea to use a smaller mesh size
around the targeted local domain. However, a rapid
change of mesh size distribution usually leads to bad
results. An adaptive mesh in FEM and a boundary-
fitted grid in FDM provide some solution to it. This
important matter will be discussed in Sect. 19.9.
4. The obtained finite element function u
h
(x) [for ex-
ample, in (19.35)] are continuous even between
elements, however, the finite element derivative
function ∂u
h
(x)/∂x is not continuous, which means
the derivative value at a node with two elements (in
the 1-D case) is not unique. To obtain the derivative
value, such as heat flux in heat conduction problems
and stress in solid mechanics (see Sect. 19.4), post-
processing is inevitable and is treated in Sect. 19.9.
5. Since a function is not defined within a grid in the fi-
nite difference method, there are no problems in the
derivations of the derivative value at a node. How-
ever you may have another problem regarding how to
select a proper definition among (19.16–19.18). Usu-
ally, the central difference scheme has a good rep-
utation due to second-order accuracy, but you need
some tricks in the multidimensional case [19.1].
6. Mathematically, FEM is governed by function anal-
ysis [19.3] since the concept of norm can be intro-
duced due to the shape of weak form. Using function
analysis, a new established finite element formula
can be evaluated in advance of real calculations in
a normal sense in functional analysis.
7. As was discussed, a finite element domain is packed
with element-wise finite element functions. Since the
field is represented by the summation of FE func-
tions, FEM is very strong at local resolution, for
example, in stress distributions in solid mechanics,
if the mesh is fine enough for the analysis. On the
contrary, if the mesh is poor (too coarse for the
problem), it is possible to obtain unexpected oscil-
lations, for example, in fluid dynamics. The stabi-
lized FEM, such as the streamline-upwind Petrov–
Galerkin method (SUPG) and the Galerkin/least
squares scheme (GLS), is one solution for it. A finite
difference domain is not filled for any functions that
are strong for unexpected oscillations, but not suit-
able for local resolution in solid mechanics.
8. As a general summary, FEM is good for arbitrary-
shaped domains, treatment of second boundary con-
ditions, solid mechanics, and parallel computations,
while FDM is only valid for regular shaped domains,
but suitable for fluid mechanics. The rough summary
table, considering other related numerical schemes,
is given in Table 19.1 in Sect. 19.9.
19.3 The Equivalence of FEM and FDM Methods
A reader might be wondering whether the treatment of
FDM and FEM are equivalent to each other. In this sec-
tion, we’ll consider the equivalence of these two forms
by explaining the variational method.
According to linear algebra [19.4], the following
three forms are equivalent, where K, f and u are a posi-
tive, definite symmetric matrix, a given force vector and
a unknown vector, respectively
(Form 1)
Ku− f =0 ,
(19.37)
(Form 2) w ·(Ku − f) =0 , ∀w ∈ R
n
,
(19.38)
(Form 3) F(v) −F(u) ≥0 , ∀v ∈R
n
,
(19.39)
where K =K
t
,
F(v) =
1
2
v ·Kv −v · f .
We now extend the discussion to the boundary-value
problem below [19.5]. Again consider the same prob-
lem as treated in Sect. 19.2 by (19.20)and(19.21),
which is Form 1 shown below. Form 2 is the weak
form already explained in (19.27). Form 3 is called the
variational form, which means the solution u is the min-
imizer of the function F(v).
(Form 1) k
∂
2
u
∂x
2
=−f in (0, 1) , u(1) =a ,
∂u
∂x
(0) =b ; (19.40)
(Form 2)
1
0
k
∂u
∂x
∂w
∂x
− fw
dz −kw(0)b =0 ,
∀w with w(1) =0 ; (19.41)
Part E 19.3
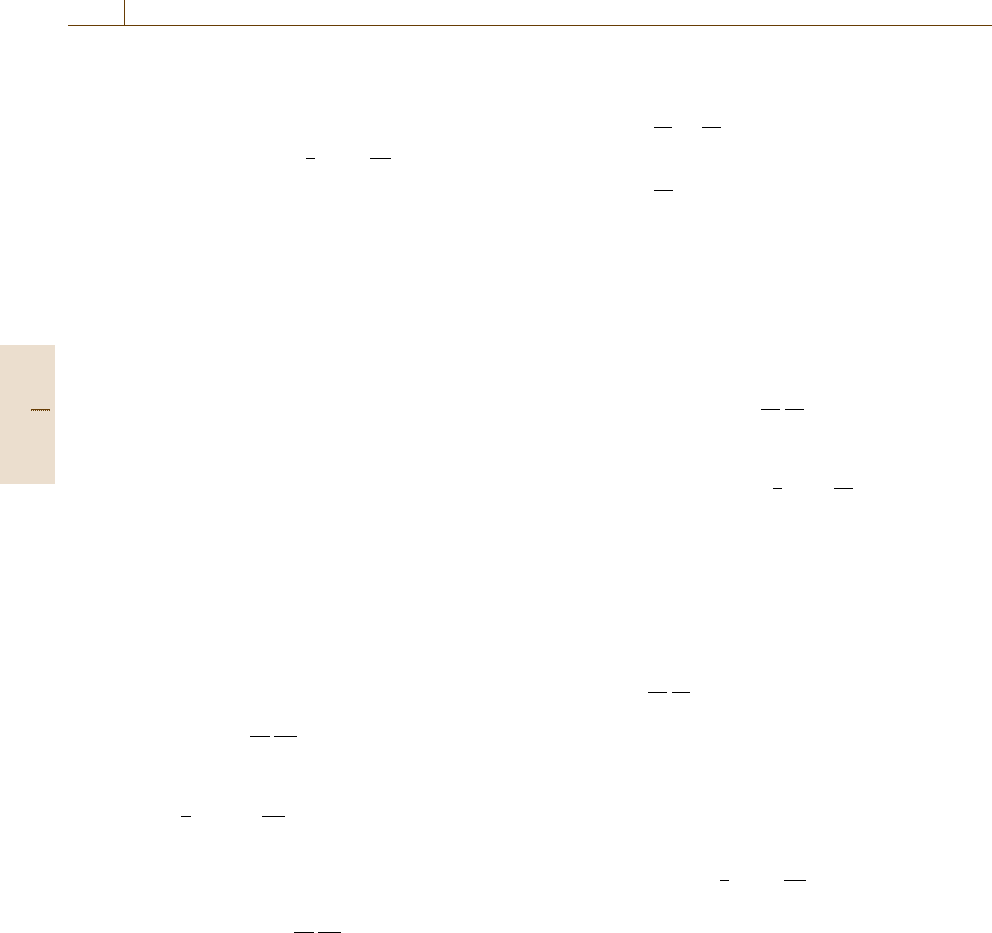
1042 Part E Modeling and Simulation Methods
(Form 3) u(1) =a , F(v) ≥ F(u) ,
∀v with v(1) =a , (19.42)
where F(v) =
1
2
1
0
k
dv
dx
2
dx
−
1
0
fv dx −kv(0)b , ∀v with v(1) =a .
First we derive Form 1 from Form 3 in the following
proof.
Proof [(Form 3) →(Form 1)]
Suppose that u is the minimizer of the function F,
which is satisfied with the given first boundary condi-
tion in the interval (0, 1)
u(1) =a , F(v) −F(u) ≥0 , ∀v with v(1) =a .
(19.43)
Substituting v =u ±εw, by introducing w, where ε is
a positive real number,
u(1) =a , F(u ±εw) −F(u) ≥0 ,
∀w with w(1) =0 . (19.44)
It should be added that w is an arbitrary function such
that w(1) =0, since v(1) =a, u(1) =a.
By rewriting (19.44),
±ε
⎡
⎣
1
0
k
∂u
∂x
∂w
∂x
− fw
dx −kw(0)b
⎤
⎦
+
1
2
ε
2
1
0
k
∂w
∂x
2
dx ≥ 0 . (19.45)
If ε →0 after dividing the equation by ε(> 0),
(Form 2)
1
0
k
∂u
∂x
∂w
∂x
− fw
dx −kw(0)b =0 .
(19.46)
By integration by part with w(1) =0,
1
0
−
∂
∂x
k
∂u
∂x
− f
wdx
+k
∂u
∂x
(0)w(0) −kw(0)b =0 . (19.47)
Since w and w(1) are arbitrary, the equation above as-
cribes to the following shape, which is nothing else but
Form 1.
Now we derive Form 3 from Form 1.
Proof [(Form 1) →(Form 3)]
Subtracting F(u) from F(v),
F(v) −F(u) =
1
0
k
∂u
∂x
∂
∂x
(v −u)− f (v −u)
dx
−k(v −u)(0)b +
1
2
1
0
k
∂
∂x
(v −u)
2
dx .
(19.48)
Since the function u and v must satisfy the first
boundary condition, (v −u)(0) =0 gives the following
equation
u(1) =a ,
1
0
k
∂u
∂x
∂
∂x
(v −u)− f (v −u)
dx
−h(v −u)(0)b =0 ,
∀v with v(1) =a . (19.49)
According to the derivations above, we finally obtain
Form 3
F(v) −F(u) =
1
2
1
0
k
d
dx
(v −u)
2
dx ≥ 0 .
(19.50)
It is recommended that one refer to the explanation in
Sect. 19.2.2 again, after reading this section.
19.4 From Mechanics to Mathematics:
Equilibrium Equations and Partial Differential Equations
Although (19.20) was given without any logical deriva-
tion, the governing partial differential equations are
always derived from both equilibrium equations in
a mechanical sense and material constitutive equations
in a material property sense. In this section, we derive
mathematics from mechanics.
The governing equations describe the relationship
between the force-related variables as input and the
Part E 19.4
Finite Element and Finite Difference Methods 19.4 From Mechanics to Mathematics: Equilibrium Equations 1043
motion-related variables as output. The equilibrium
equations represent the mechanical balancing relation-
ship, while material constitutive equations characterize
the empirical material properties of the target. In short,
the former is related to mechanics and the latter is con-
cerned with materials
Governing equations
=Equilibrium equations (from mechanical balancing)
+Material constitutive equations (from experiments).
It should be noted from Sect. 19.1 that the material
constitutive equation directly represents the governing
equationin(19.1), which is a special case.
19.4.1 Heat Conduction Problem
in the Two-Dimensional Case
Let us take a look at the balance of heat flux in an
infinitesimal element as shown in Fig. 19.13, where
q
x
and q
y
show heat fluxes, the functions of x and y,
in the x and y directions, respectively.
Considering in and out heat flux,
Q∇t =
!
q
x
x −
1
2
∇x, y
−q
x
x +
1
2
∇x, y
"
∇y
−
!
q
y
x, y −
1
2
∇y
−q
x
x, y +
1
2
∇y
"
∇x
+ f ∇x∇y
#
∇t . (19.51)
By dividing the equation above by Δx Δy Δt and taking
the limit as Δx and Δy →0, we get
lim
∇x∇y→0
Q
∇x∇y
=−
∂q
x
∂x
−
∂q
y
∂y
+ f . (19.52)
2
Δx
(x,y)
q
y
(x,y+––)
2
q
x
(x–––,y)
2
q
x
(x+––,y)
2
q
y
(x,y–––)
Δy
Δy
Δx Δx
Δy
Fig. 19.13 Balance of heat flux in an infinitesimal element
On the other hand, Q can be defined by introducing the
heat capacity c
p
and the density
Q = c
p
˙
uΔxΔy . (19.53)
Then we obtain the following equilibrium equation
c
p
˙
u =−
∂q
x
∂x
−
∂q
y
∂y
+ f . (19.54)
As for the material property of heat conduction,
Fourier’s law, which was modeled by experiments, is
known as
⎧
⎪
⎪
⎨
⎪
⎪
⎩
q
x
=−k
xx
∂u
∂x
−k
xy
∂u
∂y
,
q
y
=−k
yx
∂u
∂x
−k
yy
∂u
∂y
.
(19.55)
Combining the equilibrium heat equation and the mater-
ial constitutive equation, we finally obtain the unsteady
heat conduction equation in the two-dimensional case.
Equation (19.20) is a one-dimensional steady-state
version
c
p
˙
u =
∂
∂x
k
xx
∂u
∂x
+k
xy
∂u
∂y
+
∂
∂x
k
yx
∂u
∂x
+k
yy
∂u
∂y
+ f . (19.56)
19.4.2 Elastic Solid Problem
in the Three-Dimensional Case
Solid mechanics problems are rather complicated to ex-
plain, since there exist three components such as stress,
strain, and displacement.
What is needed now are the following.
1. Equilibrium relationship on stress;
2. Displacement–strain relationship;
3. Stress–strain relationship including material consti-
tutive equations.
The three recipes above are explained in the follow-
ing parts, to derive the governing equation of elastic
solid deformation problems. Some additional discus-
sion on stress is necessary to avoid a misunderstanding
of the physical meanings. The three-dimensional case is
treated here, since the two-dimensional case is a degen-
erated case with some additional assumptions.
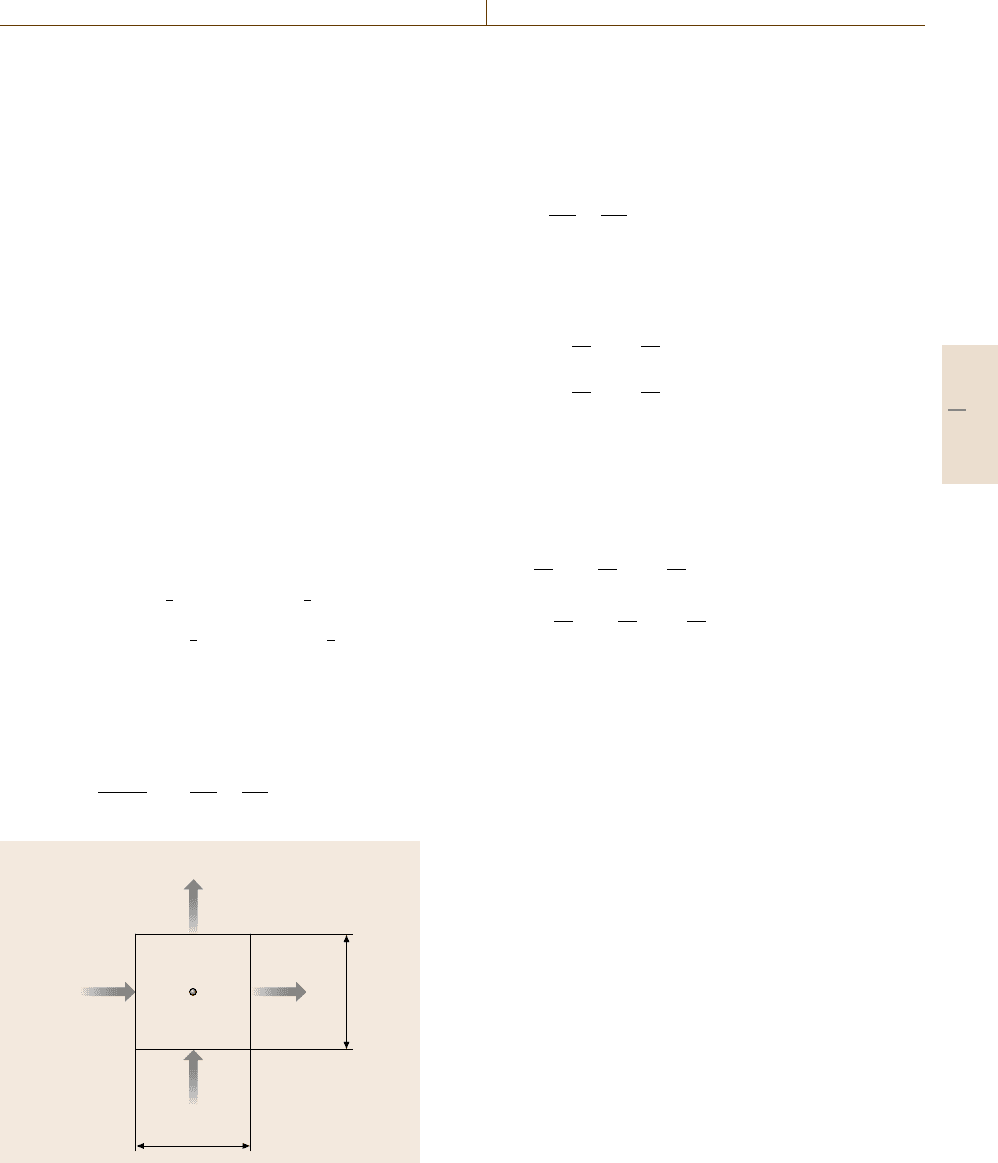
Equilibrium Relationship on Stress
Now let us think about the balance of forces in the
x-direction in a three-dimensional infinitesimal element
Part E 19.4
1044 Part E Modeling and Simulation Methods
Δy
Δy
Δy
Δx
2
σ
xx
(x+––,y,z)
2
σ
zx
(x,y,z –––)
Δz
Δz
Δz
2
σ
yx
(x,y +––,z)
2
σ
xx
(x –––,y,z)
Δx
Δx
2
σ
zx
(x,y,z+––)
2
σ
yx
(x,y –––,z)
x
z
y
Fig. 19.14 Balance of forces in the x-direction in an infinitesimal
element
in Fig. 19.14, where σ
αβ
is a stress (local pressure) value
on the α-plane (the plane perpendicular to α-coordinate)
in the β-direction, which is a function of x, y,andz.For
example, σ
zx
represents the component of stress in the
x-direction on the z-plane.
The equilibrium in the x-direction is
!
−σ
xx
x −
1
2
∇x, y, z
+σ
xx
x +
1
2
∇x, y, z
"
∇y∇z
+
!
−σ
yx
x, y −
1
2
∇y, z
+σ
yx
x, y +
1
2
∇y, z
"
∇z∇x
+
!
−σ
zx
x, y, z −
1
2
∇z
+σ
zx
x, y, z +
1
2
∇z
"
∇x∇y
+ f
x
∇x∇y∇z = 0 . (19.57)
After dividing by Δx Δy and applying Δx Δy →0, we
get
∂σ
xx
∂x
+
∂σ
yx
∂y
+
∂σ
zx
∂z
+ f
x
=0 . (19.58)
Applying the same steps in the y-andz-directions leads
to the following equations
∂σ
xy
∂x
+
∂σ
yy
∂y
+
∂σ
yz
∂z
+ f
y
=0 ,
∂σ
xz
∂x
+
∂σ
yz
∂y
+
∂σ
zz
∂z
+ f
z
=0 . (19.59)
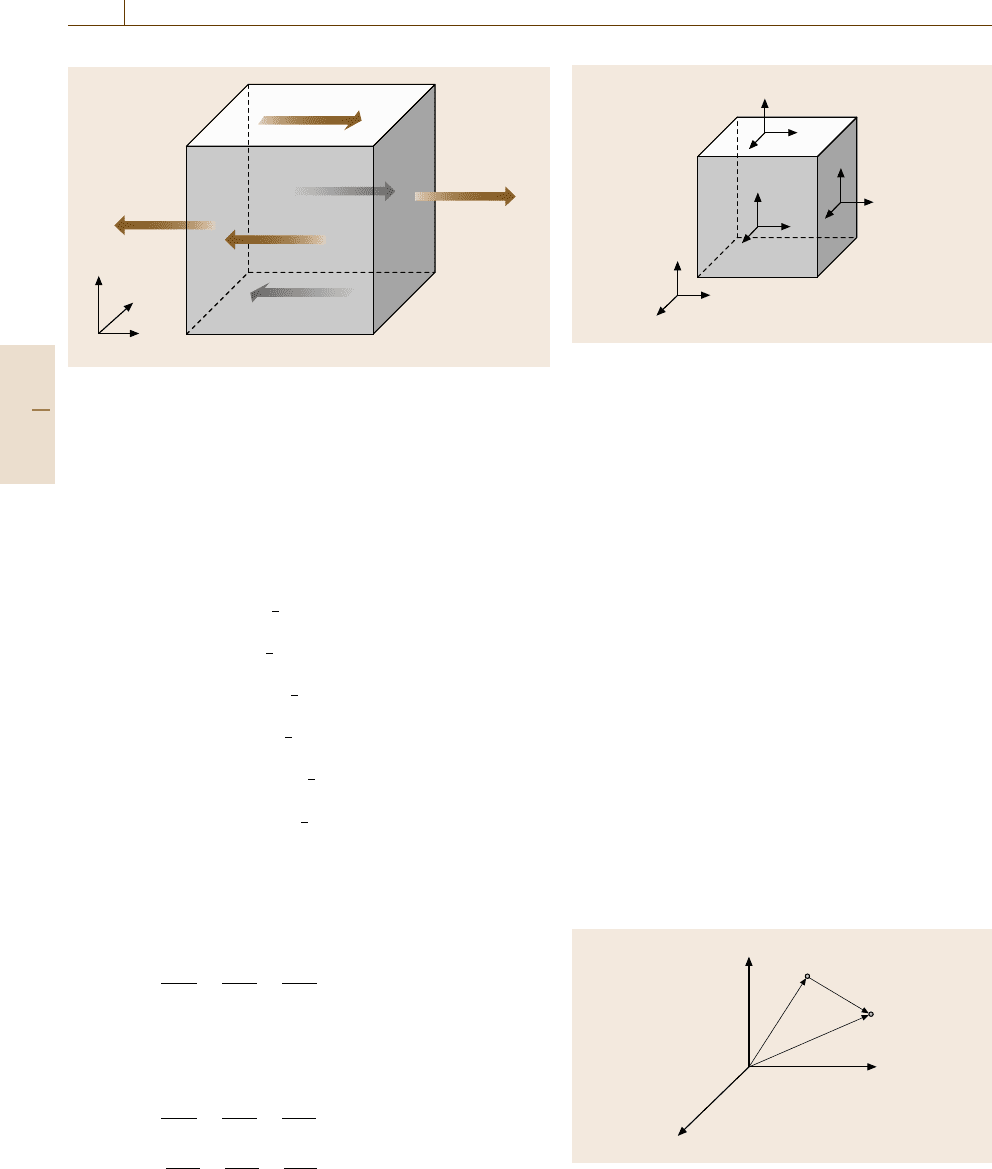
σ
zx
x
z
y
σ
yx
σ
xx
σ
zy
σ
yy
σ
xy
σ
zz
σ
yz
σ
xz
Fig. 19.15 Stress components
The stress components in (19.58)and(19.59) are some-
times represented in matrix form (19.60), which is
physically visualized in Fig. 19.15
σ =
⎛
⎜
⎝
σ
xx
σ
yx
σ
zx
σ
xy
σ
yy
σ
yx
σ
xz
σ
yz
σ
zz
⎞
⎟
⎠
. (19.60)
Considering the momentum equilibrium in Fig. 19.15,
the symmetry of the stress is obtained. The shearing
stress σ
xy
is sometimes described as τ
xy
, but the mean-
ing is the same
σ
xy
=σ
yx
,σ
yz
=σ
zy
,σ
zx
=σ
xz
. (19.61)
Displacement–Strain Relationship
Let us consider the case that a point P is moved to
a point P
after some deformation of the body, as shown
in Fig. 19.16.
Suppose vectors a and x are position vectors of
points P and P
, individually. For the convenience of
notation, subscripts 1, 2, and 3 represent x, y,andz,
x
1
(x)
x
2
(y)
x
3
(z)
a
x
u
P
P'
Fig. 19.16 Deformation
Part E 19.4
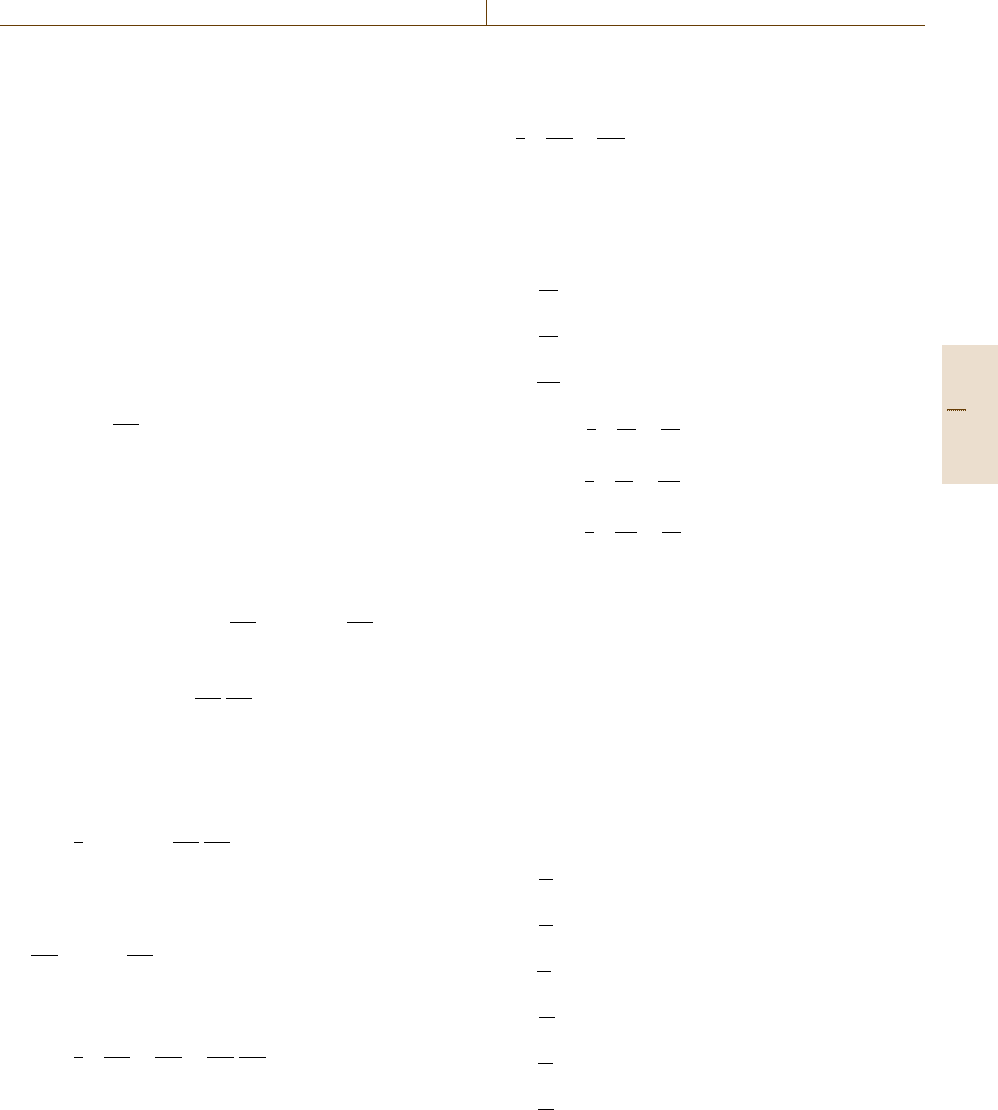
Finite Element and Finite Difference Methods 19.4 From Mechanics to Mathematics: Equilibrium Equations 1045
respectively in the following parts
u = x −a (or u
k
= x
k
−a
k
)
where x
1
= x , x
2
= y , and x
3
= z . (19.62)
If you consider a differential line near points P and P
,
then
|
dx
|
2
+
|
da
|
2
=
3
$
i=1
dx
i
dx
i
−
3
$
k=1
da
k
da
k
,
where x
1
= x , x
2
= y , and x
3
= z . (19.63)
According to the differential rule
da
k
=
3
$
i=1
∂a
k
∂x
i
dx
i
(19.64)
(19.64) changes to
3
$
i=1
dx
i
dx
i
−
3
$
k=1
da
k
da
k
=
3
$
i=1
dx
i
dx
i
−
3
$
k=1
3
$
i=1
∂a
k
∂x
i
dx
i
3
$
i=1
∂a
k
∂x
i
dx
i
=
3
$
i=1
3
$
j=1
δ
ij
−
3
$
k=1
∂a
k
∂x
i
∂a
k
∂x
j
dx
i
dx
j
. (19.65)
If the following definition of strain tensor ε
ij
is intro-
duced
ε
ij
=
1
2
δ
ij
−
3
$
k=1
∂a
k
∂x
i
∂a
k
∂x
j
(19.66)
and taking the derivative of ∂x
i
in (19.63)
∂u
k
∂x
i
=δ
ki
−
∂a
k
∂x
i
(19.67)
then we obtain
ε
ij
=
1
2
∂u
i
∂x
j
+
∂u
j
∂x
i
−
∂u
k
∂x
i
∂u
k
∂x
j
. (19.68)
If the higher term is neglected in (19.68), we obtain
the following displacement–strain relationship, which is
called a Cauchy infinitesimal strain tensor. It should be
noted that there exists a lot of stress tensors in nonlin-
ear solid mechanics that allow finite deformation and
rotation [19.6]
ε
ij
=
1
2
∂u
i
∂x
j
+
∂u
j
∂x
i
. (19.69)
As a summary, the displacement and strain are con-
nected to each other in the following relationship, where
u, v,andw are displacement in the x, y,andz directions,
respectively.
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
ε
xx
=
∂u
∂x
ε
yy
=
∂v
∂y
ε
zz
=
∂w
∂z
ε
xy
=ε
yx
=
1
2
∂u
∂y
+
∂v
∂x
ε
yz
=ε
zy
=
1
2
∂v
∂z
+
∂w
∂y
ε
zx
=ε
xz
=
1
2
∂w
∂x
+
∂u
∂z
(19.70)
Stress–Strain Relationship Including Material
Constitutive Equations
The constitutive equation for three-dimensional iso-
tropic elastic material, which describes the stress–strain
relationship, is modeled by experiments, as an extension
of Hooke’s law, where E, ν,andG are Young’s modulus
(modulus of elasticity), Poisson’s ratio, and the modu-
lus of elasticity in shear, respectively. For the definition
of Young’s modulus and Poisson’s ratio, please refer to
Sect. 19.7.1. It should be emphasized that (19.71)and
(19.72) are only valid for three-dimensional isotropic
elastic material
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
ε
xx
=
1
E
σ
xx
−ν
σ
yy
+σ
zz
ε
yy
=
1
E
σ
yy
−ν
σ
zz
+σ
xx
ε
zz
=
1
E
σ
yy
−ν
σ
xx
+σ
yy
ε
xy
=
1
G
σ
xy
ε
yz
=
1
G
σ
yz
ε
zx
=
1
G
σ
zx
(19.71)
or
σ = Dε
Part E 19.4
1046 Part E Modeling and Simulation Methods
where
σ =
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
σ
1
σ
2
σ
3
σ
4
σ
5
σ
6
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
σ
xx
σ
yy
σ
zz
σ
yz
σ
zx
σ
xy
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
, ε =
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
ε
1
ε
2
ε
3
ε
4
ε
5
ε
6
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
ε
xx
ε
yy
ε
zz
2ε
yz
2ε
zx
2ε
xy
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
,
D =
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
λ +2G λλ000
λλ+2G λ 000
λλλ+2G 000
000G 00
0000G 0
00000G
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
,
λ =
Eν
(1 −2ν)(1 +ν)
, G =
E
2(1 +ν)
. (19.72)
As in the two-dimensional case, there are two degen-
erated cases: the plane stress case is for plates with
in-plane forces imposed, while the plane strain case
is for a beam-like structure along the z direction with
equally distributed forces acting on the long side. The
former and latter are described by the conditions of
σ
zz
= σ
zx
= σ
zy
= 0andε
zz
= ε
zx
= ε
zy
= 0, respec-
tively [19.7]
⎛
⎜
⎝
σ
xx
σ
yy
σ
xy
⎞
⎟
⎠
=
⎛
⎜
⎜
⎜
⎜
⎝
E
1 −ν
2
Eν
1−ν
2
0
Eν
1 −ν
2
E
1−ν
2
0
00G
⎞
⎟
⎟
⎟
⎟
⎠
⎛
⎜
⎝
ε
xx
ε
yy
ε
xy
⎞
⎟
⎠
(plane stress case) ,
λ =
Eν
(1 −2ν)(1 +ν)
, G =
E
2(1+ν)
,
(19.73)
⎛
⎜
⎝
σ
xx
σ
yy
σ
xy
⎞
⎟
⎠
=
⎛
⎜
⎝
λ(1 −ν) λν 0
λν λ(1−ν)0
00G
⎞
⎟
⎠
⎛
⎜
⎝
ε
xx
ε
yy
ε
xy
⎞
⎟
⎠
(plane strain case) ,
λ =
Eν
(1 −2ν)(1 +ν)
, G =
E
2(1+ν)
.
(19.74)
So far, the derivation of the governing equation on
the three-dimensional isotropic elastic solid problem
has been explained. In solid mechanics, stress values
are very important and are directly linked to breakage,
crash, and fatigue. A further explanation of stress is pro-
vided below to avoid a misunderstanding of physical
meanings.
Further Explanation of Stress
Now let’s study stress more deeply. The stress (pres-
sure) value at a point cannot be determined uniquely
if the acting plane information is not given. To repre-
sent the stress condition, the information on both an
evaluation point and an evaluation plane is needed.
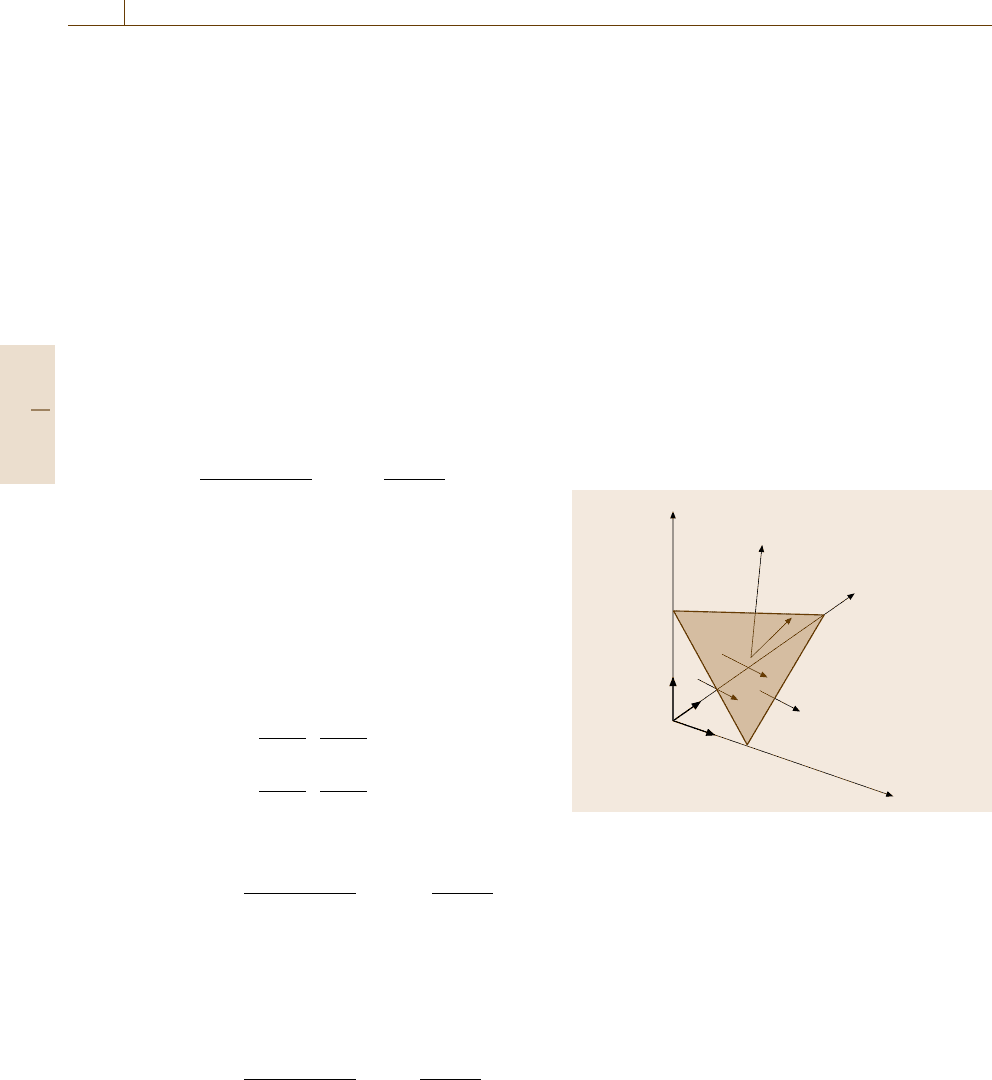
Figure 19.17 shows a tetrahedral element, where t is
a traction vector, the shaded face is a targeted plane, and
n is a normal unit vector of the targeted plane. It should
be added that the traction vector t is not an applying
force from outside to the tetrahedral, but a reaction force
from the tetrahedral element to outside.
x
z
y
σ
xx
σ
zx
σ
yx
t
n
Fig. 19.17 Stress components at a tetrahedral element
We represent the traction vector t with stress compo-
nents in xyz-coordinates. Considering the x direction
in Fig. 19.17, we get the following equation, where
ΔA, ΔA
α
, ΔV, ,and f
x
are the area of the shaded
plane, the area of α-plane (tetrahedral face normal to
α-coordinate), the volume of the tetrahedral, the density,
and the x component of the volume force
σ
xx
ΔA
x
+σ
yx
ΔA
y
+σ
zx
ΔA
z
− f
x
ΔV = t
x
ΔA .
(19.75)
Since ΔA
x
=n
x
ΔA,...(n
x
is x component of the nor-
mal unit vector n), we get
(σ
xx
n
x
+σ
yx
n
y
+σ
zx
n
z
)ΔA − f
x
ΔV = t
x
ΔA .
(19.76)
Part E 19.4
Finite Element and Finite Difference Methods 19.5 From Mathematics to Mechanics: Characteristic of Partial Differential Equations 1047
Considering ΔA → 0 (at the same time, ΔV →0),
t
x
=σ
xx
n
x
+σ
yx
n
y
+σ
zx
n
z
,
t
y
=σ
xy
n
x
+σ
yy
n
y
+σ
zy
n
z
,
t
z
=σ
xz
n
x
+σ
yz
n
y
+σ
zz
n
z
, (19.77)
or
⎛
⎜
⎝
t
x
t
y
t
z
⎞
⎟
⎠
=
⎛
⎜
⎝
σ
xx
σ
yx
σ
zx
σ
xy
σ
yy
σ
zy
σ
xz
σ
yz
σ
zz
⎞
⎟
⎠
⎛
⎜
⎝
n
x
n
y
n
z
⎞
⎟
⎠
. (19.78)
Now the traction force vector t on the shaded plane is
represented with a stress component matrix σ in (19.78)
and a normal vector. It should be noted that the stress
matrix σ is a second-rank tensor since it contains the di-
rectional information of acting force and imposed plane.
Mathematically the 3 ×3 matrix has the following
important properties.
1. It has three eigenvalues, including multiple roots,
which are real numbers.
2. The eigenvectors are orthogonal to each other.
With these properties the stress matrix can be trans-
formed as follows after some coordinate changes. The
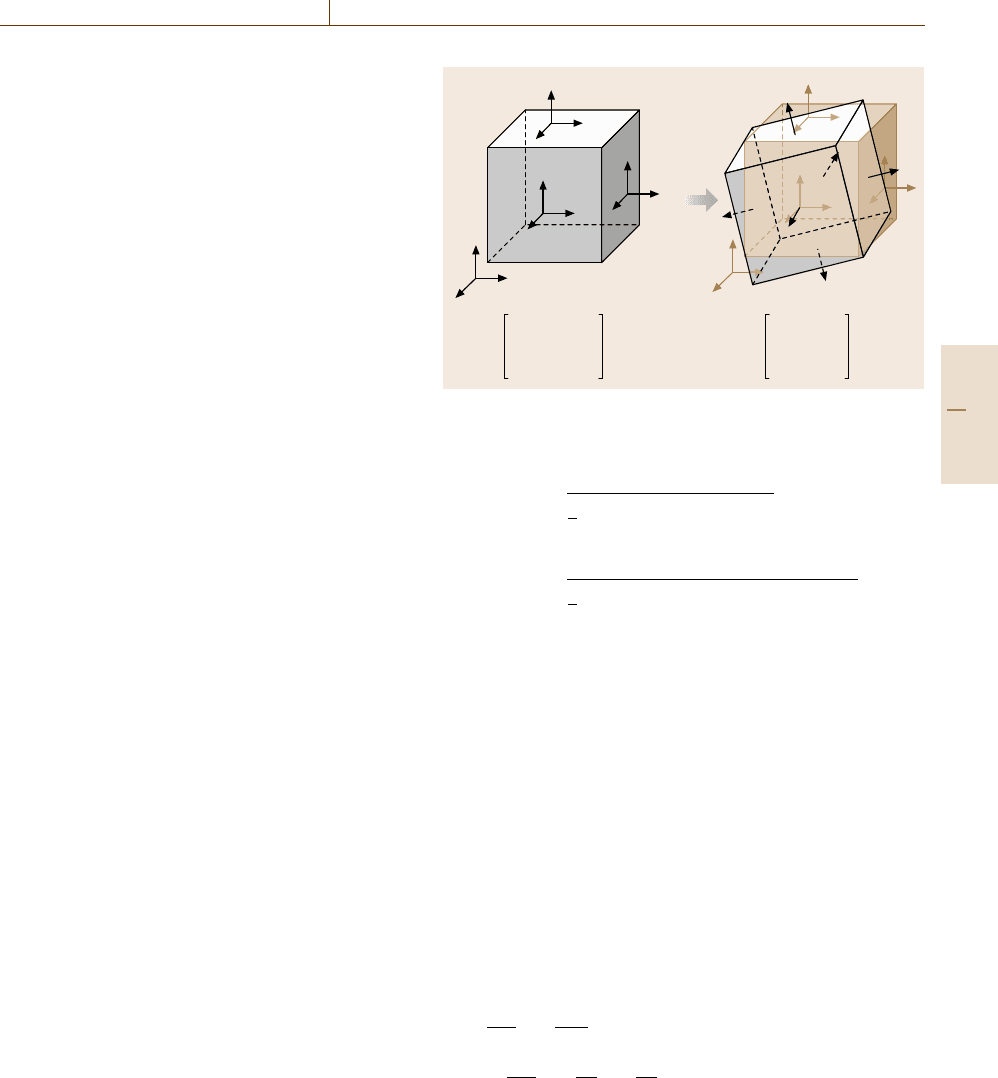
physical meaning is illustrated in Fig. 19.18, where σ
x
,
σ
y
,andσ
z
are called the principal stress. It should be
added that the left and right sides of Fig. 19.18 are phys-
ically identical since the transformation is just a change
of coordinate setting.
The 3 × 3 stress matrix has three invariants against
coordinate settings. The von Mises stress value in
(19.79), which is a good estimator of the strength, is
σ
zx
x
z
y
σ
yx
σ
xx
σ
zy
σ
yy
σ
xy
σ
zz
σ
yz
σ
xz
x
z
y
σ
x
σ
y
σ
z
σ
xx
σ =
σ
yx
σ
zx
σ
xy
σ
yy
σ
yx
σ
xz
σ
yz
σ
zz
σ
x
σ =
00
0 σ
y
0
00σ
z
Fig. 19.18 Principal stresses
one of them
σ
von Mises
=
%
&
&
&
'
1
2
!
σ
x
−σ
y
2
+
σ
y
−σ
z
2
+
(
σ
z
−σ
x
)
2
"
=
%
&
&
&
'
1
2
!
σ
xx
−σ
yy
2
+
σ
yy
−σ
zz
2
+
(
σ
zz
−σ
xx
)
2
"
+3
σ
2
xy
+σ
2
yz
+σ
2
zx
.
(19.79)
It must be added in this section that these governing
equations are only valid for continuum mechanics since
the material constitutive equations are derived from
experimental data obtained in a continuum modeling
sense.
19.5 From Mathematics to Mechanics:
Characteristic of Partial Differential Equations
In the previous section, we studied the derivation of
mathematical governing equations for heat conduction
problems and solid deformation problems from me-
chanical points of view. In this section, we take a look
at the characteristics of physical (mechanical) represen-
tations of partial differential equations, categorized in
a mathematical sense.
Equation (19.80) represents the general form of
second-order partial differential equations
A
∂
2
φ
∂x
2
+B
∂
2
φ
∂x∂t
+C
∂
2
φ
∂t
2
+D
∂φ
∂x
+E
∂φ
∂t
+Fφ +G = 0 . (19.80)
Part E 19.5
