Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing

Подождите немного. Документ загружается.

1058 Part E Modeling and Simulation Methods

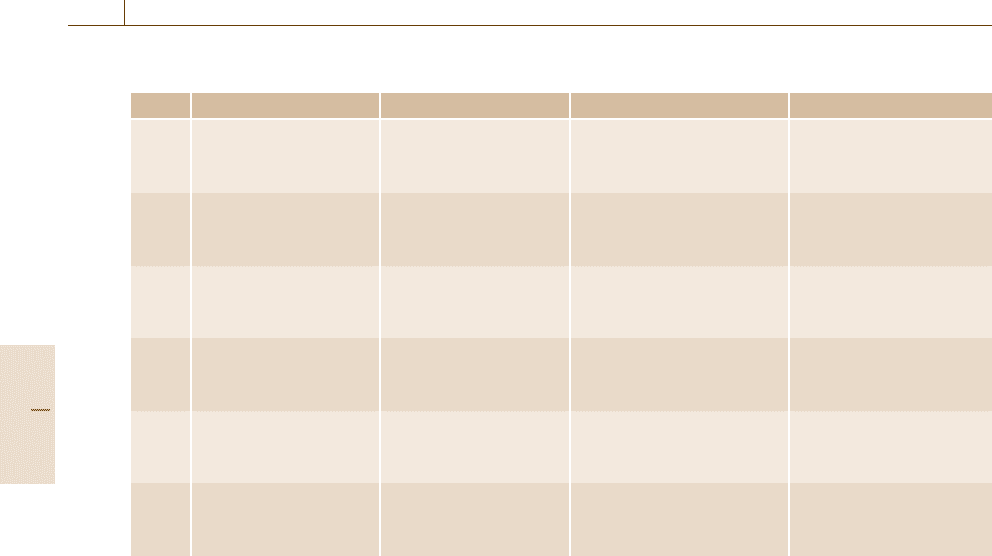
Table 19.1 Summary of discretized numerical schemes

Strong points Weak points Major targets Software

FEM 2nd BC treatment Calculation time Nonlinear solid/thermal/ﬂuid/ ANSYS (multiphysics)

Local resolution Complex derivation vibration LS-DYNA (crash/solid)

Arbitrary shape Sensitive solution FIDAP (ﬂuid), etc.

FDM Calculation time Stable solution Simple derivation Flow-3D (ﬂuid), etc.

Stable solution Regular shape

Simple derivation Heuristic aspects

FVM Calculation time Local resolution Thermal/ﬂuid FLUENT (ﬂuid), etc.

Stable solution Heuristic aspects

Moving boundary

BEM Simple modeling Limited to linear/ Linear elastic/linear ﬂow/ BEASY (solid), etc.

homogeneous case acoustic/magnetic

Dense matrix

CIP Complex problem New method Thermal/ﬂuid/solid [19.17]

Stable solution No sales software

Multiphysics

PM No mesh/grid Calculation time Nonlinear solid/explosion [19.18]

Explosion New method

Highly nonlinear No sales software

greatly affects the calculation time and required mem-

ory size, some renumbering algorithms to reduce the

bandwidth are proposed.

The iterative methods can be classiﬁed into two

groups: (1) The stationary iterative methods, such as

the Jacobi method, Gauss–Seidel method, and suc-

cessive overrelaxation (SOR) method, and (2) the

nonstationary method, such as the conjugate gradi-

ent (CG) method, the biconjugate gradient stabilized

(Bi-CGSTAB) method, quasiminimal residual (QMR)

method, and generalized minimal residual (GMRES)

method [19.21]. The rough algorithm in the stationary

iterative methods can be represented by (19.126)

Ax =b → Mx =(M−A)x +b ,

k+1

=(M−A)x

+b , (19.126)

where (1) M = diagonal part of A,(2)M = triangular

part of A,and(3)M = combination of (1) and (2) part

of A.

The basic algorithm on nonstationary method is

represented in (19.127), where r, p,andx are the resid-

ual vector, direction vector, and the solution vector,

respectively.

=b−Ax

for k =0, 1, 2,...

k+1

= p

+αr

k+1

= x

+β p

k+1

=b−Ax

k+1

convergence check

end. (19.127)

To accelerate convergence of the iterations, the al-

gorithm with some preconditioners is proposed as

in [19.21]

=b−Ax

for k =0, 1, 2,...

−1

k+1

= p

+αz

k+1

= x

+β p

k+1

=b− Ax

k+1

convergence check

end.

Some of the related subroutines above are available

from [19.22].

For the parallel calculation method such as the do-

main decomposition method, please refer to [19.23]

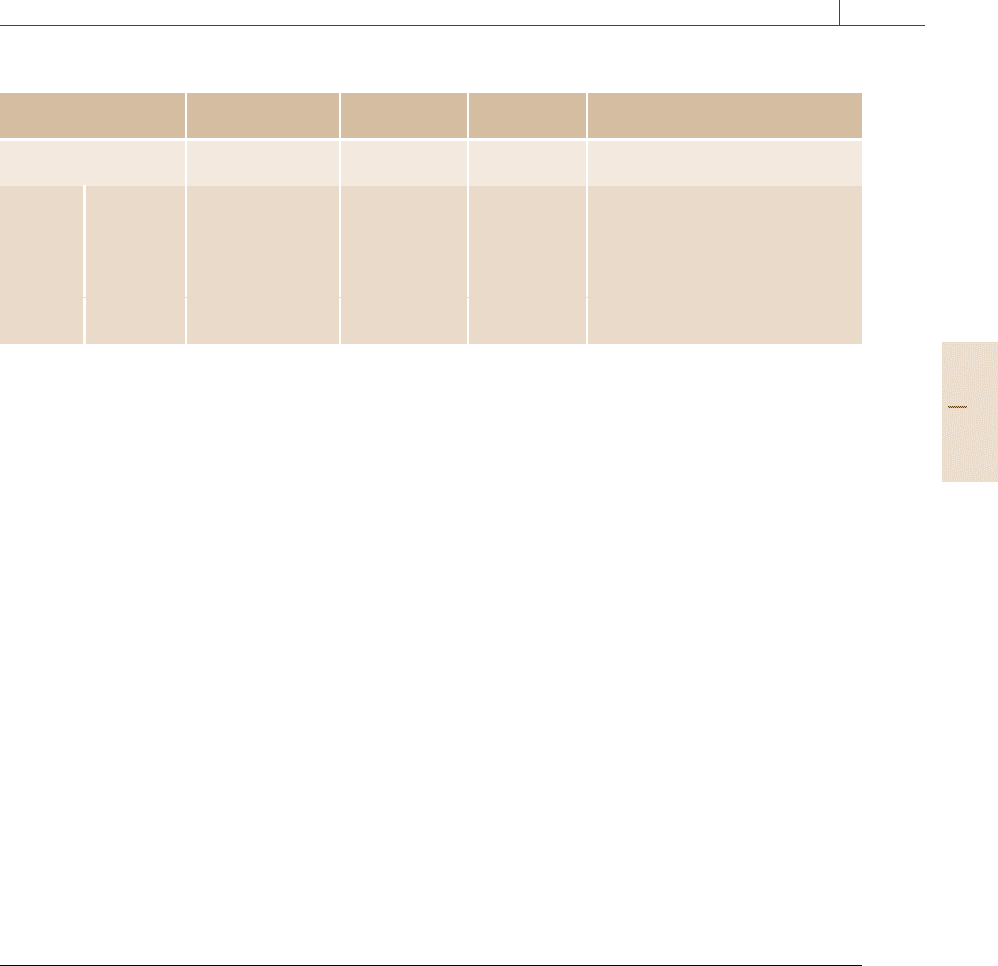
and [19.24]. Table 19.2 shows the summary of matrix

calculation methods.

Part E 19.9

Finite Element and Finite Difference Methods References 1059

Table 19.2 Summary of matrix calculation methods

For ill-conditioned For parallel Method

matrix calculation

Direct matrix solver ◦ × Skyline Symmetric

Frontal Nonsymmetric

Iterative Stationary × ◦ Jacobi M =diagonal part of A

matrix Gauss–Seidel M =triangular part of A

solver SOR M =diagonal and triangular parts of A

Non- × ◦ CG Symmetric/FEM/solid

stationary Bi-CGSTAB Nonsymmetric/FEM/solid

QMR Nonsymmetric/FEM/ﬂuid

GMRES Nonsymmetric/FEM/ﬂuid

19.9.6 Multiscale Method

To bridge the macroscopic scale and mezoscopic scale,

the multiscale approach was recently considered to be

important. The homogenization method is one of the so-

lutions that carries numerical material testing between

macroscale (usual FE mesh) and microscale (FE mesh

at material level) to get real-time stress–strain constitu-

tive behavior for FEA in macroscale. The key points of

this method are introduced in reference [19.25].

19.10 Free Codes

Some internet URLs for FEM and FDM are provided

for the reader’s convenience. This is not a recommended

selection; the reader must use the information at their

own risk.

1. Information on modeling, FEM,andFDM

http://homepage.usask.ca/∼ijm451/ﬁnite/fe_

resources/fe_resources.html (Internet Finite Ele-

ment Resources; general information on FEM

including free codes)

http://morden.csee.usf.edu/dragon/kpalbrec/mesh.

html (Meshing Research Corner; survey of mesh

generation schemes and codes)

2. Parallel computations in FEM, FDM,andFVM

http://www.ibase.aist.go.jp/infobase/pcp/platform-

en/index.html (Parallel Computing Platform/PCP

developed by AIST and FUJIRIC; perfect solution

for parallelization of FEM/FDM/FVM codes, free

from headaches from matrix handling, MPI com-

mands and memory allocations, sample programs of

FEM/FDM/FVM are also provided)

3. Related libraries

http://www.netlib.org/ (collection of mathematical

software, papers, and databases)

4. Modeling-related free software

http://www.netlib.org/voronoi/index.html (Voronoi;

2-dimensional Voronoi diagram, Delaunay triangu-

lation)

http://www.geuz.org/gmsh/ (Gmsh mesh generation

code with TRI/QUAD/TETRA/HEXA element)

References

19.1 J.W. Thomas: Numerical Partial Differential Equa-

tions: Finite Difference Methods (Springer, Berlin,

Heidelberg 1995)

19.2 T.J.R. Hughes: The Finite Element Method: Linear

Static and Dynamic Finite Element Analysis (Dover,

New York 2000)

19.3 A.N. Kolmogorov, S.V. Fomin: Elements of the The-

ory of Functions and Functional Analysis (Dover,

New York 1999)

19.4 G. Strang: Introduction to Applied Mathematics

(Wellesley-Cambridge, Cambridge 1986)

19.5 N. Kikuchi: Finite Element Methods in Mechanics

(Cambridge Univ. Press, New York 1986)

19.6 T.Belytschko,W.K.Liu,B.Moran:Nonlinear Finite

Elements for Continua and Structures (Wiley, New

York 2000)

19.7 S.P. Timoshenko, J.N. Goodier: Theory of Elasticity

(McGraw-Hill, New York 1970)

Part E 19

1060 Part E Modeling and Simulation Methods

19.8 O.C. Zienkiewicz, D.V. Phillips: An automatic mesh

generation scheme for plane and curved surfaces

by isoparametric coordinate, Int. J. Numer. Meth-

ods Eng. 3, 519–528 (1971)

19.9 J.F. Thompson, Z.U.A. Warsi, C.W. Mastin: Numer-

ical Grid Generation (North-Holland, Amsterdam

1985)

19.10 A. Tezuka: 2D mesh generation scheme for adaptive

remeshing process, Jpn. Soc. Mech. Eng. 38,204–

215 (1996)

19.11 A.M. Winslow: Numerical solution of the quasi-

linear poisson equation in a nonuniform triangle

mesh, J. Comput. Phys. 2, 149–172 (1967)

19.12 M. Ainsworth, J.T. Oden: A Posterior Error Estima-

tion in Finite Element Analysis (Wiley, New York

2000)

19.13 P.J. Roache: Veriﬁcation and Validation in Com-

putational Science and Engineering (Hermosa,

Socorro 1998)

19.14 R. Peyret: Handbook of Computational Fluid Me-

chanics (Academic, New York 1996)

19.15 K.A. Woodbury: Inverse Engineering Handbook

(CRC, Boca Raton 2002)

19.16 J.H. Ferziger, M. Peric: Computational Methods for

Fluid Dynamics (Springer, Berlin, Heidelberg 2001)

19.17 C.A. Brebbica: The Boundary Element Method for

Engineers (Pentech, London 1978)

19.18 T. Nakamura, R. Tanaka, T. Yabe, K. Takizawa:

Exactly conservative semi-Lagrangian scheme for

multidimensional hyperbolic equations with di-

rectional splitting technique, J. Comput. Phys. 174,

171–207 (2001)

19.19 CIPUS (CIP User’s Society): www.mech.titech.ac.jp/

~ryuutai/cipuse.html (2011) by T. Yabe

19.20 W.K. Liu, S. Li: Meshfree and particle methods

and their applications, Appl. Mech. Rev. 55,1–34

(2002)

19.21 G.H. Golub, C.F. Van Loan: Matrix Computations

(Johns Hopkins Univ. Press, Baltimore 1996)

19.22 W.H. Press, S.A. Teukolsky, W.T. Vetterling,

B.P. Flannery: Numerical Recipes in Fortran 90:

The Art of Parallel Scientiﬁc Computing, 2nd edn.

(Cambridge Univ. Press, Cambridge 1996)

19.23 B.F. Smith, P.E. Bjrstad, W.D. Gropp: Domain De-

composition: Parallel Multilevel Methods for Elliptic

Partial Differential Equations (Cambridge Univ.

Press, Cambridge 1996)

19.24 Parallel Computing Platform/PCP: www.ibase.aist.

go.jp/infobase/pcp/platform-en/index.html (2011)

19.25 J.M. Guedes, N. Kikuchi: Preprocessing and post-

processing for materials based on the homog-

enization method with adaptive ﬁnite element

methods, Comput. Methods Appl. Mech. Eng. 83,

143–198 (1990)

Part E 19

1061

The CALPHAD

20. The CALPHAD Method

Phase diagrams offer various areas of materials

science and technology indispensable informa-

tion for the comprehension of the properties of

materials. The microstructure of solid materials is

generally classiﬁed according to the size of the con-

stituents – for example, at the electron, atomic, or

granular level (Sect. 1.3). Accordingly, fundamen-

tal principles like quantum mechanics, statistical

mechanics, or thermodynamics are applied indi-

vidually to describe the physical properties. Phases

are important features of material because they

characterize homogeneous aggregations of matter

with respect to chemical composition and uniform

crystal structure. The various functions of a mater-

ial are closely related to the phases and structures

of the material’s composition. Therefore, to de-

velop a material with a maximum level of desired

functions, it is essential to undertake design of the

structure in advance.

Phase diagrams are composed by means of

experimental measurements, as well as statisti-

cal thermodynamic analysis. The construction of

phase diagram calculations based on experiments

and thermodynamic analysis are generally referred

to as the calculation of phase diagrams (CALPHAD)

approach [20.1]. This method provides a very ac-

curate understanding of the properties originating

in the macroscopic character of the material under

study.

This chapter is organized in three parts:

•

In the ﬁrst part, a brief outline of the CALPHAD

method is summarized.

•

In the second part, the method for deriving the

Gibbs free energies incorporating the ab initio

calculations is presented in order to clarify the

uncertainty of thermodynamic properties for

metastable solution phases, taking the Fe

−

Be-

based bcc phase as an example. Some results

20.1 Outline of the CALPHAD Method..............1062

20.1.1 Description of Gibbs Energy ...........1062

20.1.2 Equilibrium Conditions .................1064

20.1.3 Evaluation

of Thermodynamic Parameters.......1065

20.2 Incorporation of the First-principles

Calculations into the CALPHAD Approach . 1066

20.2.1 Outline

of the First-principles Calculations . 1066

20.2.2 Gibbs Energies of Solution Phases

Derived by the First-principles

Calculations.................................1067

20.2.3 Thermodynamic Analysis

of the Gibbs Energies Based

on the First-principles Calculations 1071

20.2.4 Construction of Stable

and Metastable Phase Diagrams.....1071

20.2.5 Application

to More Complex Cases..................1073

20.3 Prediction of Thermodynamic Properties

of Compound Phases with

First-principles Calculations ..................1079

20.3.1 Thermodynamic Analysis

of the Fe–Al–C System ..................1079

20.3.2 Thermodynamic Analysis

of the Co–Al–C and Ni–Al–C

Systems ......................................1083

References ..................................................1090

for metastable phase equilibria in the Fe

−

Be,

and Co

−

Al binary systems are shown.

•

In the third part the application to predict ther-

modynamic properties of compound phases is

discussed. The thermodynamic modeling for

thePerovskitecarbidewithanE2

-type struc-

ture in the Fe

−

C, Co

−

C and Ni

−

ternary systems is illustrated, and constructions

of phase diagrams are performed.

Part E 20

1062 Part E Modeling and Simulation Methods

20.1 Outline of the CALPHAD Method

Phase diagrams provide basic and important infor-

mation especially for the design of new materials.

However, by using experimental techniques only, a lot

of time and labor is required in construction of even

a partial region of a phase diagram, because the practical

materials are composed of multicomponent alloys, more

than ternary systems. In order to break this difﬁcult situ-

ation, the method of calculation of phase diagrams was

advocated and is referred to as the CALPHAD method.

CALPHAD was originally a name for this researcher’s

group, however it has recently become the name for the

technique by which a phase diagram is calculated on the

basis of thermodynamics. In this method a variety of ex-

perimental values concerning the phase boundaries and

the thermodynamic properties is analyzed according to

an appropriate thermodynamic model and the interac-

tion energies between atoms are evaluated. By using

this technique, phase diagrams outside the experimen-

tal range can be calculated based on thermodynamic

proof. Difﬁculty in extension of the calculated results

to higher-order systems is much less than that in the

case of experimental work, since the essence of the cal-

culation does not change so much between a binary

system and a higher-order system. This method pro-

vides a very accurate understanding of the properties

originating in the macroscopic character of the material

under study. However, a shortcoming of this approach

is that it is hard to obtain information on metastable

equilibria, or on undiscovered phases, since the ther-

modynamic parameters from this method can only be

evaluated from experimental data.

The empirical model of de Boer et al. [20.2]hasof-

ten been used to deduce the thermodynamic quantities

of systems where the experimental values do not exist.

In this model, generally called Miedema’s model, the

crystal lattice is divided into Wigner–Seitz cells. The

simple expression for the formation energy in alloys is

derived by considering the change in the electron den-

sity states at the interface between the cells, as shown

in (20.1)

ΔE ∝−P

(

ΔΦ

)



Δn

1/3



. (20.1)

Here, Δn

is the difference in electron density based

on the volume of the Wigner–Seitz cell between differ-

ent species of atoms. This term always leads to local

perturbations that give rise to a positive energy con-

tribution in (20.1). On the other hand, ΔΦ presents

a difference between the chemical potentials of the dif-

ferent species of atoms at the cell surfaces, and leads to

an attractive term in (20.1). The constants P and Q are

proportionality constants, derived empirically. Equa-

tion (20.1) does not contain any parameters that refer

to the crystal structure, and therefore, the heats of solu-

tion of face-centered-cubic (fcc), body-centered-cubic

(bcc), and hexagonal-close-packed (hcp) structures, as

well as liquids, are predicted. However, it is known that

the absolute values are not always predicted accurately,

although this model predicts the correct sign for the for-

mation enthalpy in various alloy systems. For example,

thermodynamic analysis of the Fe

−

Pd system predicts

the enthalpy of formation for the L1

and the L1

ordered phases to be −14 kJ/mol and −22 kJ/mol, re-

spectively, while the predicted values from Miedema’s

model are −6kJ/mol for the L1

phase and −4kJ/mol

for the L1

phase [20.3]. The large difference between

these values means that incorporating Miedema’s model

with a thermodynamic analysis is rather difﬁcult.

Such serious problems, which are intrinsic to the

CALPHAD approach, should be solved with the as-

sistance of the ﬁrst-principles energetic calculation

method. Thus, in the present chapter, a new approach

to introduce some thermodynamic quantities obtained

by the ab initio band energy calculations in the conven-

tional CALPHAD-type analysis of some alloy systems

is presented.

20.1.1 Description of Gibbs Energy

Gibbs Free Energy

Using the Regular Solution Approximation

The selection of a thermodynamic model by which

Gibbs free energy of an alloy system is described is

the most important factor when using the CALPHAD

method. In a system in which interaction between alloy-

ing elements is not so strong, the regular solution model

is well known to describe the thermodynamic properties

of the alloys comparatively well. For instance, the free

energy of the A

−

B binary alloy is expressed as (20.2)

= x

+RT(x

ln x

) , (20.2)

where

is the Gibbs energy of the pure component i

in the standard, and x

is the mole fraction of i. L

shows the interaction energy for A atoms and B atoms,

and is given by

= NZ



−

(

+ε

)



, (20.3)

Part E 20.1

The CALPHAD Method 20.1 Outline of the CALPHAD Method 1063

where N denotes the so called Avogadro’s number, Z is

the coordination number, and ε

, ε

and ε

show

the cohesion energies between A–B, A–A, B–B atomic

pair, respectively. The ordering between unlike atoms

occurs for L

< 0 because the A–B atom pair is more

stable than the average of the A–A and B–B atom pairs.

On the other hand, the clustering of the like atom is

caused in case of L

> 0. For L

= 0, no atomic

interaction exists, and then the solution shows the ran-

dom mixing of atoms. This interaction parameter should

not be constant but a function of the temperature and

the chemical compositions of alloys. From a qualita-

tive point of view, the ﬁrst term of (20.2) represents the

energies of mechanical mixing, the second term stands

for excess energy which shows deviation from the ideal

solution, and the third is ideal mixing entropy.

Gibbs Free Energy Using the Sublattice Model

For the simplest case of the sublattice model [20.4],

let us consider a phase represented by the formula

(A, B)

(C, D)

, containing two elements A and B in one

sublattice “1” and two elements C and D in the other

sublattice “2”. The coefﬁcients a and b show the number

of sites in each sublattice and the size of the sublattices

may be generally chosen as a +b =1 for convenience.

There are four elements in the system, however the de-

grees of freedom in varying in composition are two,

because the total numbers of atoms in each sublat-

tice are ﬁxed. Thus these two composition parameters

are conveniently plotted on a square where the corners

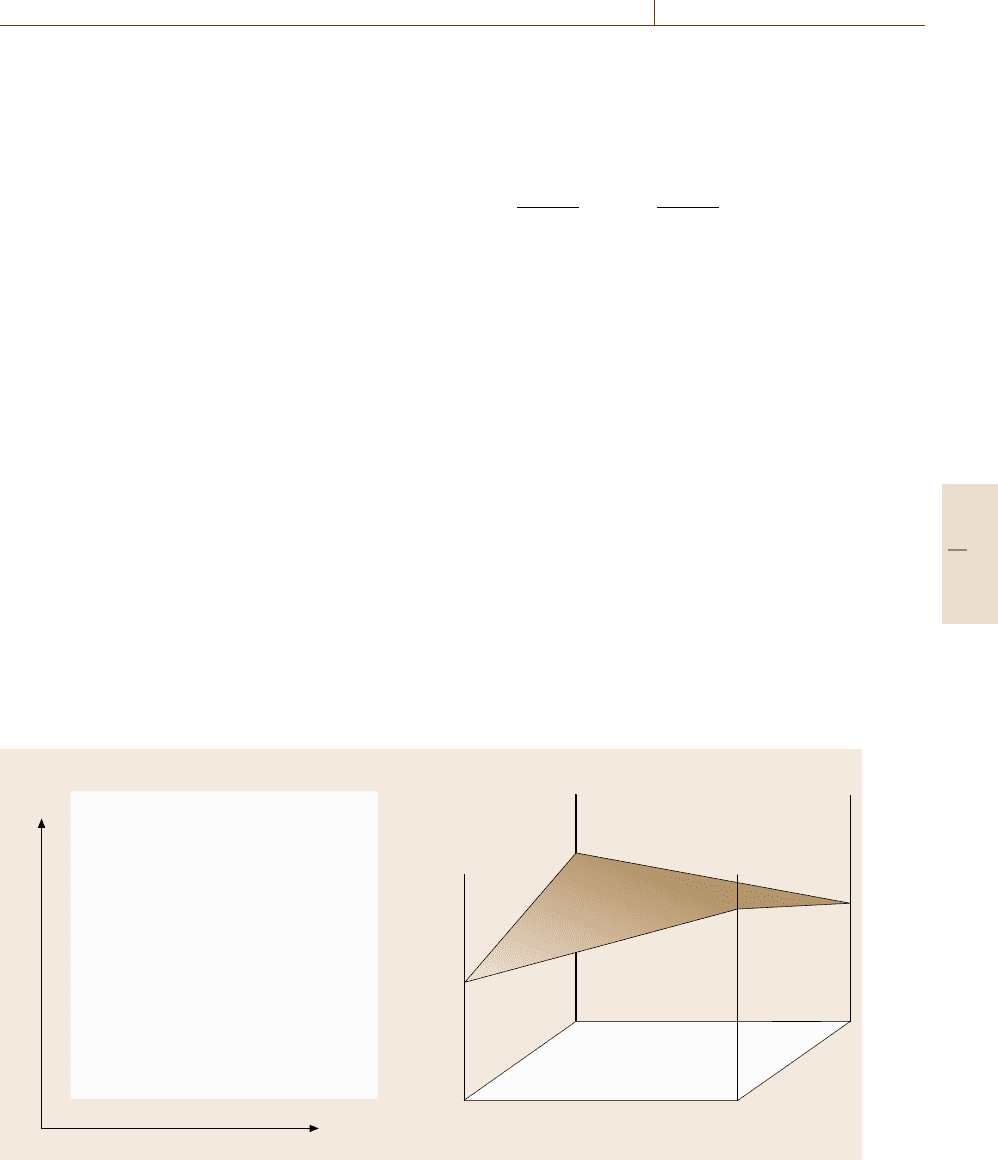
Fig. 20.1 (a) Composition square in a quaternary system (A, B)

(C, D)

and (b) surface of reference for the free energy

represented the four basic end members A

,andB

, as shown in Fig. 20.1a. The symbols

and y

denote the mole fractions, respectively, for

the sublattices 1 and 2, and they are represented as fol-

lows:

, y

. (20.4)

In this equation n

denotes the number of i atoms in

the j sublattice. The nonplanar surface composed of

four reference states, i. e., one each for the compounds

,andB

, is called the surface of

reference as shown in Fig. 20.1b, and represented by

ref

= y

. (20.5)

For the entropy term, the following Gibbs energy of

mixing can be obtained, assuming the atoms mix ran-

domly within each sublattice

ideal

mix

= RT





ln y





ln y



. (20.6)

It seems difﬁcult to accept that the interaction between

A and B atoms should be quite independent of whether

the other sublattice is occupied by C and D atoms. Thus

the regular solution model should be deﬁned as the

power series representation of excess Gibbs free energy

Part E 20.1

1064 Part E Modeling and Simulation Methods

by the following equation

mix

= y

A,B:C

A,B:D

A:C,D

B:C,D

(20.7)

where L

i, j:k

(or L

i:j,k

) is the interaction parameter

between unlike atoms on the same sublattice. Conse-

quently the Gibbs energy for one mole of the phase,

denoted as (A, B)

(C, D)

, can be represented by the

two-sublattice model as shown in (20.8):

= G

ref

ideal

mix

. (20.8)

Gibbs Energy for Interstitial Solutions

Represented by Sublattice Model

The Gibbs energy for interstitial phases is very impor-

tant in steels and ferrous alloys, where the elements

such as C, N, S, or B occupy the interstitial sites of

solid solutions. The structure of such a phase is consid-

ered as consisting of two sublattices, one occupied by

substitutional elements and the other occupied by the

interstitial elements as well as vacancies. Let us con-

sider the austenite phase for the Fe

−

C system, for

instance. The occupation of the sublattices is shown as

(Cr, Fe)

(C, Va)

, since the number of sites in each sub-

lattice is 1 :1 in the case of an fcc structure. The Gibbs

energy is given by the following equation:

= y

Cr:Va

Fe:Va

Cr:C

Fe:C

+RT



ln y





ln y





Cr,Fe:Va



−y





Cr,Fe:C



−y





Cr:C,Va



−y





Fe:C,Va



−y



(20.9)

The ﬁrst two terms represent the Gibbs energy of fcc Cr

and Fe, because the second sublattice consists of vacan-

cies. The next two terms represent the Gibbs energy of

the CrC and FeC compounds, where the interstitial sites

are completely ﬁlled with C. The second line shows the

ideal entropy term, while the residual lines represents

the excess terms of the Gibbs energy. When y

= 0in

the equation, the Gibbs energy equation coincides with

the equation for the simple substitutional mixing of Cr

and Fe.

Magnetic Contribution to Gibbs Energy

In magnetic materials containing Fe, Ni and Co, there

is polarization of electron spins, and it is necessary to

consider the magnetic contribution to the Gibbs energy,

by adding the extra term to the paramagnetic Gibbs

energy G

as follows:

G = G

mag

. (20.10)

The magnetic contribution to the Gibbs free energy,

mag

, is given by the expression

mag

= RTf (τ)ln(β +1) , (20.11)

where

f (τ) =1−



79τ

−1

140p

474

497



−1





135

600



, for τ<1

(20.12)

and

f (τ) =−



−5

−15

315

−25

1500



, for τ ≥1 ,

(20.13)

and

A =

518

1125

11 692

15 975



−1



. (20.14)

The variable τ is deﬁned as T/T

, where T

is the

Curie temperature and β is the mean atomic moment ex-

pressed in Bohr magnetons μ

. The value of p depends

on the structure, and p =0.28 for the fcc phase.

20.1.2 Equilibrium Conditions

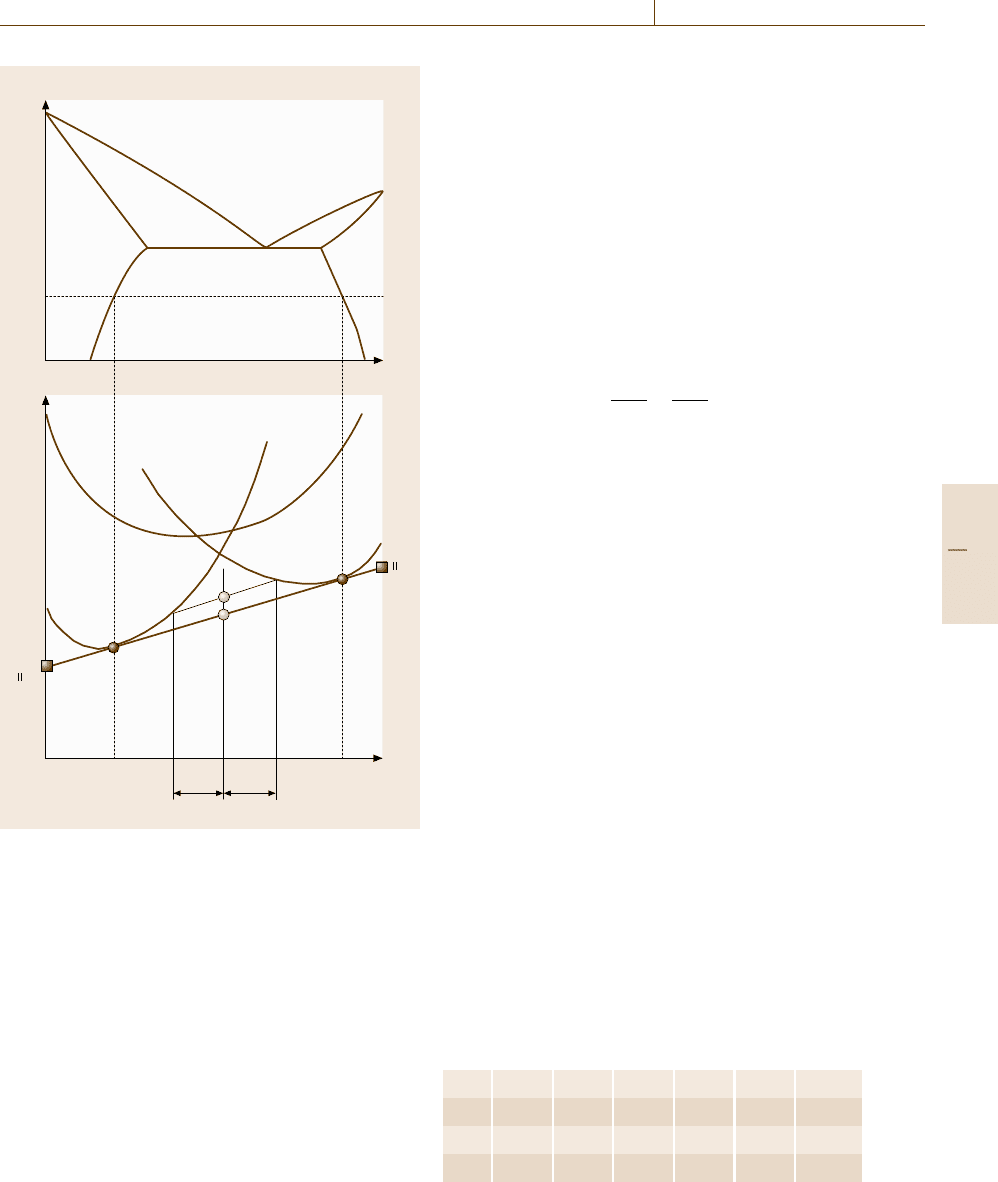
Figure 20.2 shows the so-called Gibbs energy-

composition diagram for the A

−

B binary system. This

ﬁgure schematically shows the relationship between

a eutectic type of binary phase diagram and the Gibbs

energy curves of each phase. Let us consider the case in

which the microstructure of the alloy is composed of the

Part E 20.1

The CALPHAD Method 20.1 Outline of the CALPHAD Method 1065

Temperature

Liq

Gibbs energy

Liq

Content

Fig. 20.2 Eutectic type of phase diagram and correspond-

ing Gibbs energy-composition diagram for hypothetical

−

B binary system

α and β phases. When the Gibbs energies of the α and

β phases are given by the points a





and b





, re-

spectively, the total energy of the solution is represented

by the line a

in the ﬁgure. At the alloy composition

, the Gibbs energy is G

and each phase has the vol-

ume fraction of f

and f

. Then the following relation

holds:

= G

. (20.15)

The thermodynamic equilibrium is achieved under the

condition of the lowest energy of the alloy. According to

this criterion, the point G

is not the lowest energy state,

but decreases further to G

by changing f

and f

The line a

is a common tangent of Gibbs energy G

and G

, and the equilibrium composition of each phase

is given as x

and x

. In the calculation of the phase

equilibrium, it is convenient to use these chemical po-

tentials as the basic equations. For instance, to obtain

the equilibrium between phase α and phase β,(20.16)

should be calculated by using the numerical analytic

method

=μ

. (20.16)

The chemical potential μ of each element is obtained by

using

= G

−



j=1

∂G

∂x

∂G

∂x

(20.17)

and hence the chemical potentials of A and B species in

the φ phase are expressed as:

+RT ln x





+RT ln x





. (20.18)

20.1.3 Evaluation

of Thermodynamic Parameters

The interaction parameters included in the free energy

expression can be directly evaluated from the experi-

mental values on activity. For example the activity of

Pb over the Pb

−

Sb binary liquid have been determined

asshowninTable20.1 [20.5]. The liquid state of the

elements is adopted as its standard. If the composition

dependency of the interaction parameter is expressed

as (20.19), the chemical potential of Pb in the binary

system can be derived as (20.20)

PbSb



−x



PbSb

, (20.19)

+RT ln x



1−x





PbSb



−1



PbSb



. (20.20)

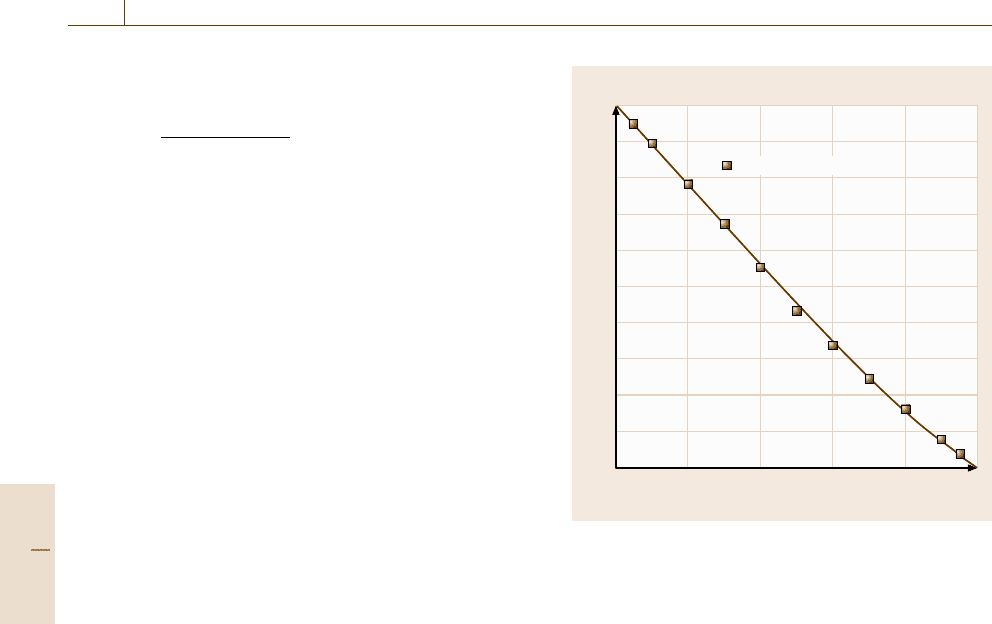
Table 20.1 Experimental data on activity of Pb in the

−

Sb binary liquid

0.05 0.1 0.2 0.3 0.4 0.5

0.04 0.08 0.162 0.247 0.338 0.433

0.6 0.7 0.8 0.9 0.95

0.555 0.674 0.785 0.897 0.946

Part E 20.1

1066 Part E Modeling and Simulation Methods

This is straightforwardly arranged as

RT ln







1 −x





PbSb

−

PbSb



+4x

PbSb

(20.21)

since the relation μ

+RT ln a

holds. There-

fore, if the left-hand side of (20.21) is calculated from

the activity data shown in Table 20.1 and the each value

is plotted against x

, the interaction parameters

PbSb

can be obtained, respectively, from the intercept

of the ordinate and the slope of the straight line as:

PbSb

=−2900 J/mol ,

PbSb

=−200 J/mol .

(20.22)

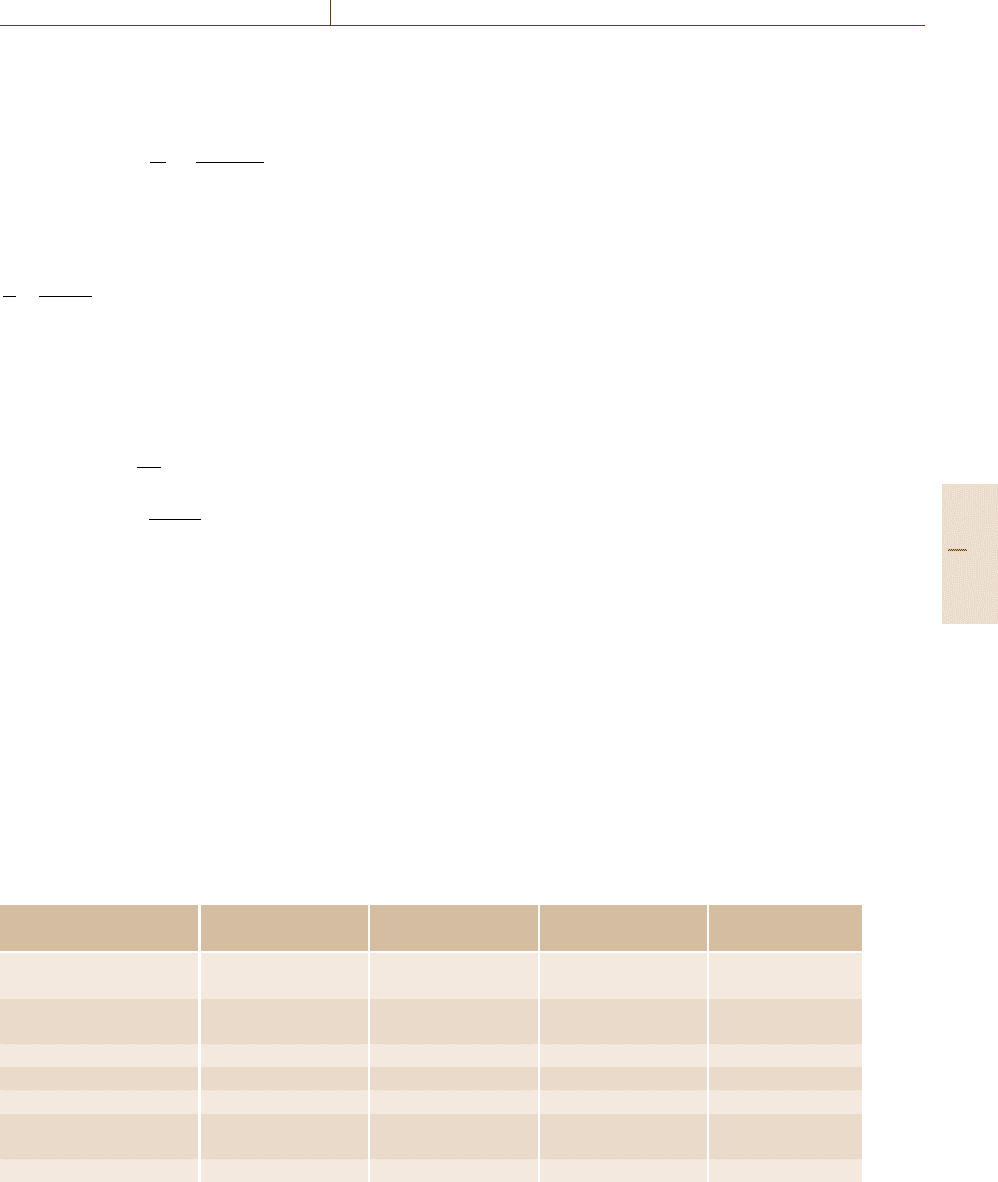
The calculated activity of Pb in the liquid phase

was compared with the experimental values in Fig. 20.3.

Considering the other observed data set at a different

temperature yields the dependence on the temperature

for the interaction parameters

PbSb

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0 0.2 0.4 0.6 0.8 1

Sb/atom fraction

Activity of Pb

Oelsen et al. (903 K)

Fig. 20.3 Calculated activity of Pb in the Pb

−

Sb binary

liquid compared with experimental values [20.5]

20.2 Incorporation of the First-principles Calculations

into the CALPHAD Approach

In this section, in order to clarify the uncertainty

of thermodynamic properties for metastable solution

phases, the method for deriving the Gibbs free en-

ergies incorporating the ﬁrst-principles calculations is

presented, taking the Fe

−

Be-based bcc phase as the

example. First, a set of some superstructures is se-

lected to be representative of a series of bcc-based

ordered phases, and the total energies are calculated

using the ﬁrst-principles calculations. Next, the effec-

tive cluster interaction energies can be extracted from

these formation energies using the cluster expansion

method (CEM). This leads to a set of composition-

independent parameters, from which the energy of

the set of superstructures can be reproduced in terms

of a set of correlation functions. Once we know the

cluster interaction energies for the alloy system, the

enthalpy term is expressed by the combination of ef-

fective cluster interaction and the correlation functions

for the clusters. The entropy term in the Gibbs en-

ergy expression is calculated using the cluster variation

method (CVM) with the tetrahedron approximation to

calculate the conﬁgurational entropy. Minimizing the

grand potential with respect to all the correlation func-

tions allows for the Gibbs energy of mixing to be

obtained as a function of composition at a constant

temperature.

20.2.1 Outline

of the First-principles Calculations

First-principles calculations using density functional

theory (DFT) have proved to be quite reliable in con-

densed matter physics. There still remains a barrier to

overcome in application to materials science, for in-

stance, stoichiometric deviations, surfaces, impurities,

and grain boundaries, however, for certain materials, the

direct application of this technique has been attempted

in studying the various properties using 100 or more

atoms in a unit cell. According to the theorem based

on DFT, the total energy E

tot

of a nonspin-polarized

system of interacting electrons in an external poten-

tial is given as a function of the ground state electronic

Part E 20.2

The CALPHAD Method 20.2 Incorporation of the First-principles Calculations into the CALPHAD Approach 1067

density ρ as in the following equation:

tot

(ρ) =



V(r)ρ(r)d

r +T[ρ]



ρ(r)ρ(r



)

|r −r



r d



[ρ].

(20.23)

Here the ﬁrst term



V(r)ρ(r)d

r denotes the Coulomb

interaction energy between the electrons and nu-

clei, T[ρ] is the single-particle kinetic energy,



ρ(r)ρ(r



)

|r−r



r d



is the Hartree component of the

electron–electron energy, and E

[ρ] is the exchange-

correlation functional.

Kohn and Sham [20.6] showed that the correct

density in the equation is given by the self-consistent so-

lution of a set of single particles following Schrödinger-

like equations as

(r) =



−



∇

+V(r) +e



ρ(r



)

|r −r



(r)



(r) .

(20.24)

In (20.24), V

represents the exchange correlation

potential and V

(r) =∂E

[ρ]/∂ρ(r). Thus we can

obtain an appropriate electronic density in much eas-

ier way as compared with solving a many-body

Schrödinger equation. In calculations, the single par-

ticle Kohn–Sham equation in (20.24) is solved sepa-

rately on a grid of sampling points in the irreducible

part of the Brillouin zone, and the obtained orbitals are

used to construct the charge density.

The ﬁrst-principles calculations based on DFT may

be, at this time, divided into two methods; one employ-

ing pseudopotentials and relatively simple basis sets,

Table 20.2 Comparison of the estimated formation enthalpies for some ordered structures with the appropriate evaluated

data

Alloy Structures Temperature Experimental values Calculated values

systems (K) (kJ/mol) (kJ/mol)

−

Ni B2 298 −71.7 −69.5

298 −41.0 −40.5

−

Ti L1

298 −39.8 −39.6

(Ti

Al) 298 −27.5 −27.3

−

Cu B2 298 −21.4 −19.0

−

Pd B2 298 −15.6 −13.2

−

Ti B2 298 −51.6 −46.5

−

Ti B2 999 −34.2 −34.1

(Ni

Ti) 827 −54.0 −51.4

−

Li B32 298 −22.8 −23.1

and the other using much more complex basis sets such

as the full potential linearized augmented plane wave

(FLAPW), which gives accurate results on formation

energies for metals. The FLAPW method, as embodied

in the WIEN2k software package [20.7], is one of the

most accurate schemes for electronic calculations, and

allows for very precise calculations of the total energies

in a solid, and will be employed in the present ener-

getic calculations. The FLAPW method uses a scheme

for solving many-electron problems based on the lo-

cal spin density approximation (LSDA) technique. In

this framework, a unit cell is divided into two regions:

nonoverlapping atomic spheres and an interstitial re-

gion. Inside the atomic spheres, the wave functions of

the valence states are expanded using a linear combina-

tion of radial functions and spherical harmonics, while

a plane wave expansion is used in the interstitial re-

gion. The LSDA technique includes an approximation

for both the exchange and correlation energies, and it

has been recently enhanced by the addition of elec-

tron density gradient terms to the exchange-correlation

energy. This has led to a generalized gradient approxi-

mation (GGA), as suggested by Perdew et al. [20.8], and

we used this improved method rather than the LSDA

approach.

20.2.2 Gibbs Energies of Solution Phases

Derived by the First-principles

Calculations

The formation enthalpies of some binary ordered struc-

tures derived by the ﬁrst-principles calculations are

compared with experimental data in Table 20.2 [20.9].

In this comparison, alloy systems where the thermo-

dynamic analysis had already been completed, are

Part E 20.2