Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing

Подождите немного. Документ загружается.

1078 Part E Modeling and Simulation Methods

–20 –15 –10 –5 0 5

Total density of states

Energy E (eV)

–20 –15 –10 –5 0 5

Energy E (eV)

Al (DO

)

Al (DO

)

A(Al)

2000

1800

1600

1400

1200

1000

800

600

400

Ni 20 40 60 80 Al

Temperature T(K)

Al (mol. %)

A(Ni)

NiAl

+B2

Fink

Alexander

Phillips

Taylor

Nash

Robertson

Hilpert

Verhoeven

Jia

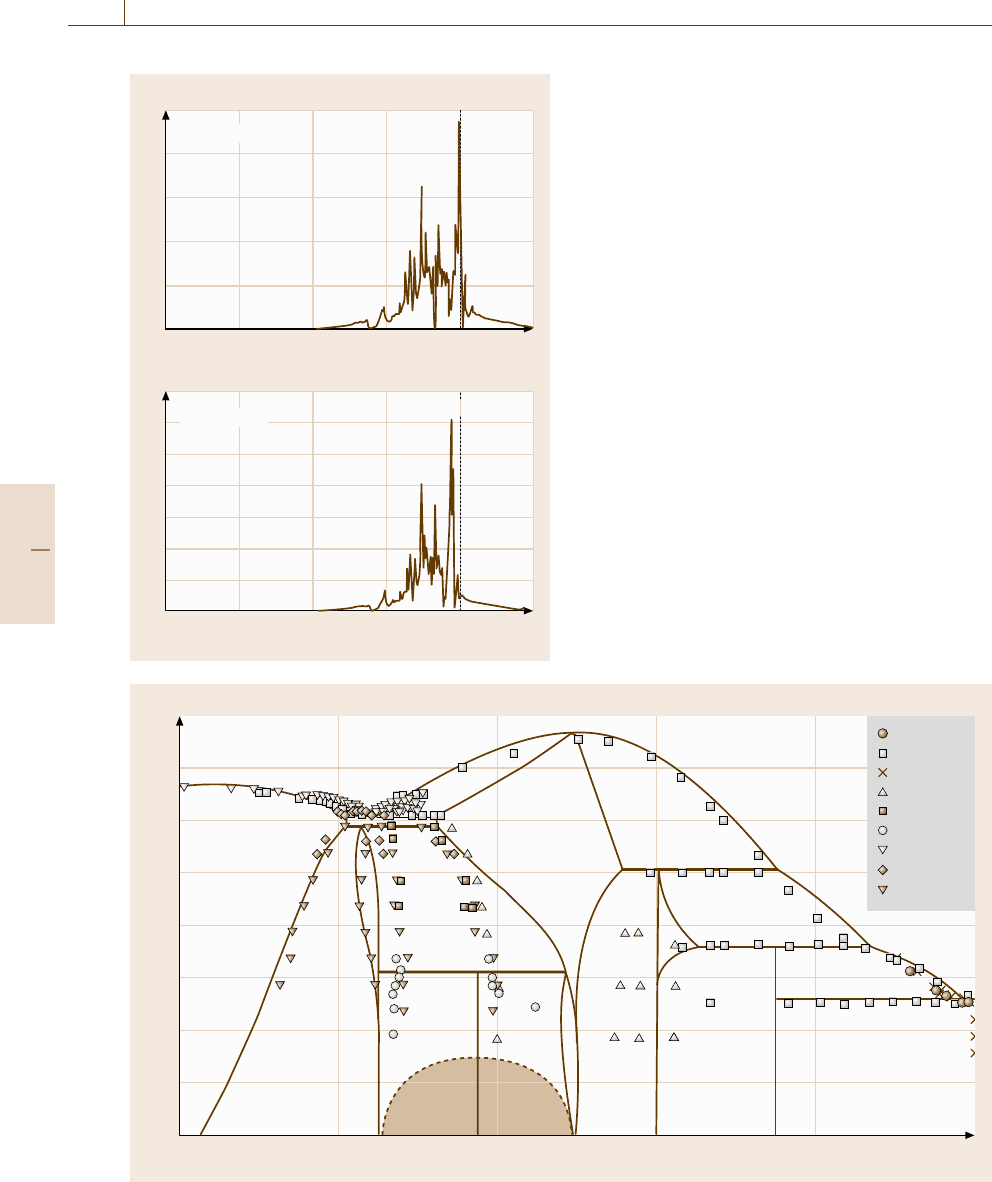
Fig. 20.17 The density of states of the D0

structure in the

−

Al and Ni

−

Al alloy systems

This difference in the density of states at the Fermi

level might be considered to be the result of the ex-

tra d-electron in Ni versus Co. From the point of view

of the rigid band approximation, this difference in the

number of electrons for two neighboring elements shifts

the Fermi level towards the higher energy side in the

−

Al system versus the Co

−

Al system. This raises

the different relative positions of the Fermi level in the

DOS curve, which consequently leads to the different

structural stabilities.

The ground state analysis of the Ni

−

Al system

suggests that the phase separation concerning the D0

structure forms at absolute zero. When assuming that

such a two-phase separation forms at a ﬁnite tempera-

ture, however, the agreement between the calculated

phase boundaries and experimental data is insufﬁcient.

For example, Fig.20.18 shows the phase diagram in the

case that a two-phase separation between the metastable

and B2 structures occurs around 500

◦

C. The

homogeneity range of the B2 single phase is compar-

Fig. 20.18 The calculated Ni

−

Al phase diagram assuming

that the critical temperature of the two-phase separation be-

tween the metastable D0

and B2 structures was around

500

◦

Part E 20.2

The CALPHAD Method 20.3 Prediction of Thermodynamic Properties of Compound Phases with First-principles Calculations 1079

atively reduced owing to the inﬂuence of the metastable

miscibility gap with decreasing temperature, and ac-

cordingly, the calculated phase boundaries deviate from

the experimental data. Therefore, the phase separation

of the D0

structure is not likely in the experimentally

observable temperature range.

20.3 Prediction of Thermodynamic Properties of Compound Phases

with First-principles Calculations

In an analysis of phase equilibria containing compound

phases, physical properties of metastable structures are

often required. The necessity appears clearly for in-

stance in the following case. Figure 20.19 shows the

isothermal phase diagram for the Fe

−

C ternary

system. In this ternary system, several types of carbides

form in which some amount of alloying element is sol-

uble. If we consider the cementite, Cr substitutes more

than 10% of Fe, and it forms the ternary line compound.

In such a case, the Gibbs energy of the cementite phase

is usually described by using sublattice model as the

(Fe, Cr)

C formula. Then if we want to evaluate the

thermodynamic function for this phase, we need the

formation energy of Cr

C, which is metastable in the

−

C binary system. In the procedure of CALPHAD

approach, this parameter is usually determined on the

basis of the experimental data in the Fe-rich side. How-

ever, it could be easily understood that this technique

follows large amount of errors in estimation. Applying

the ﬁrst-principles calculation may possibly solve this

difﬁculty. Thus in the present section, some examples

for application to predicting thermodynamic properties

of compound phases and phase diagram calculations

will be illustrated.

Carbides and nitrides play a key role in the micro-

structure control of steels, due to a ﬁne disper-

sion of these precipitates. The effectiveness of the

ﬁrst-principles calculations to the analysis of thermo-

dynamic properties of these compounds might be an

interesting issue. A comparison of the calculated forma-

tion energies with the experimental values is attempted

for some typical carbides observed in steels to clarify

the validity of the FLAPW method. Table 20.8 [20.18]

shows the formation energy, ΔE

form

,deﬁnedbyaver-

aging the total energy of the constituent elements with

chemical composition up to the segregation limit, as

follows

ΔE

form

= E

tot

−x

tot

−



1 −x



tot

, (20.37)

where φ denotes the type of carbide, and M and C rep-

resent a metallic element and graphite, respectively. For

example, the formation energy of Fe

C in the paramag-

netic state is calculated to be 17.9kJ/mol, while the

formation energy of Fe

C, by considering the spin po-

larization, is 8.1kJ/mol. This result shows the effect

of the ferromagnetism of the Fe

C phase in the lower

temperature region. Furthermore, because the formation

energy from bcc-Fe and graphite is positive, the Fe

structure is less stable than graphite at absolute zero.

The calculated formation energies for the Cr

and

phases show a reasonable agreement with the

thermodynamic data reported in the literature [20.19].

From consideration of the data shown in Table 20.8,the

thermodynamic properties for metallic carbides evalu-

ated by the ﬁrst-principles calculations can be applied to

the general procedures used in the CALPHAD method.

20.3.1 Thermodynamic Analysis

of the Fe–Al–C System

The Perovskite carbide in this ternary system, Fe

AlC

(κ), is an fcc-based ordered phase with an E2

-type

Fe Cr

Cr (at. %)

C (at. %)

20 40 60

α +M

γ+ M

Fig. 20.19 The isothermal phase diagram for the Fe

−

Cternary

system

Part E 20.3

1080 Part E Modeling and Simulation Methods

Table 20.8 Comparison of the calculated formation energies with the experimental values for some typical steel carbides

Carbides Space Calculated lattice Observed lattice Calculated formation Observed formation

group parameter (nm) parameter (nm) enthalpy in the ground enthalpy at 25

◦

state (kJ/mol) (kJ/mol)

C Pnma a =0.4871 − +17.9 −

(paramagnetic) b =0.6455 − −

c =0.4330 − −

C Pnma a =0.5018 a =0.5078 +8.1 +6.3

(ferromagnetic) b =0.6650 b =0.67297

c =0.4460 c =0.45144

Pnma a = 0.4373 a =0.4526 −19.8 −22.8

b =0.6772 b =0.7010

c =1.1730 c =1.2142

Fm-3m a =1.0475 a = 1.06595 −21.8 −19.7

structure. The application of this material as a heat

resistant alloy from the formation of a coherent ﬁne

microstructure consisting of an fcc solid solution and

the κ phase is attracting great attention [20.20]. Regard-

less of such a promising potential for this new material,

little information on the thermodynamic properties of

this carbide phase is known. Thus, an attempt to calcu-

late the full phase equilibria of the Fe

−

C ternary

system is made, introducing the ﬁrst-principles val-

ues for Fe

AlC into a CALPHAD-type thermodynamic

analysis.

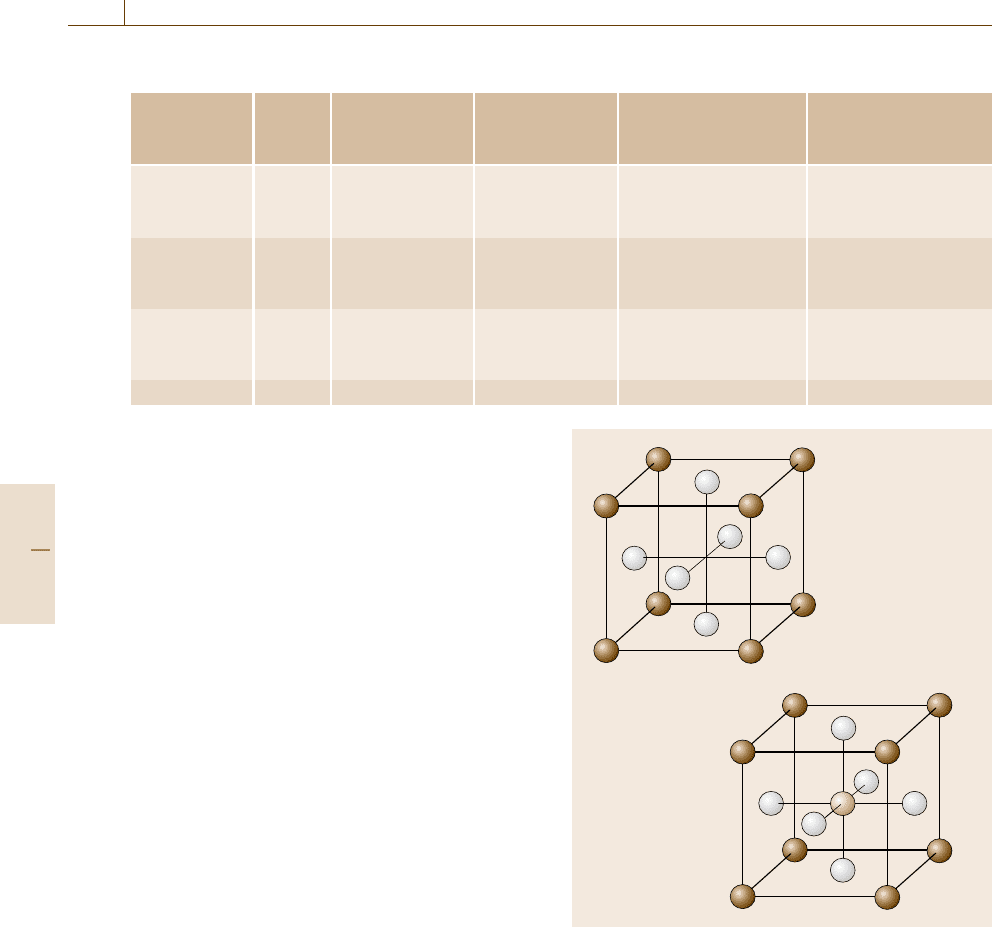
In the Fe

AlC structure, the Fe and Al atoms are ar-

rangedinanL1

-type superlattice, in which the C atoms

occupy interstitial sites, resulting in an E2

superstruc-

ture. Figures 20.20a, 20.20b show schematic diagrams

of the Fe

Al–L1

and Fe

AlC–E2

structures, respec-

tively. If the C atom occupies only the body-centered

sites, then it is surrounded by six Fe atoms, and this is

preferable from an energetic point of view. Occupation

of the other fcc interstitial sites enhances the tetrag-

onality of the L1

crystal structure, yielding a larger

strain energy. The only difference between these two

structures is the existence of C atoms in the octahedral

interstitial sites. Therefore, the Gibbs free energies of

these two ordered structures should be described by the

same thermodynamic model. The two-sublattice model

denoted by the formula,



(1)





(2)



was generally applied to the L1

structure, and the

three-sublattice model,



(1)





(2)





(3)



Al-L1

AlC-E2

Fig. 20.20a,b Crystal structures for (a) Fe

Al–L1

and

(b) Fe

AlC–E2

is applied to the κ phase. The Gibbs free energy for the

κ phase is calculated using (20.38):

= y

(1)

(2)

(3)

Al:Al:C

(1)

(2)

(3)

Al:Al:Va

(1)

(2)

(3)

Al:Fe:C

(1)

(2)

(3)

Al:Fe:Va

(1)

(2)

(3)

Fe:Al:C

(1)

(2)

(3)

Fe:Al;Va

Part E 20.3

The CALPHAD Method 20.3 Prediction of Thermodynamic Properties of Compound Phases with First-principles Calculations 1081

(1)

(2)

(3)

Fe:Fe:C

(1)

(2)

(3)

Fe:Fe:Va

+3RT



(1)

ln y

(1)

ln y

(1)



+RT



(2)

ln y

(2)

ln y

(2)



+RT



(3)

ln y

(3)

ln y

(3)



(1)

(2)

(3)

Al,Fe:Al:C

(1)

(2)

(3)

Al,Fe:Fe:Va

(1)

(2)

(3)

Al,Fe:Fe:C

(1)

(2)

(3)

Al,Fe:Fe:Va

(1)

(2)

(3)

Al:Al,Fe:C

(1)

(2)

(3)

Al:Al,Fe:Va

(1)

(2)

(3)

Fe:Al,Fe:C

(1)

(2)

(3)

Fe:Al,Fe:Va

(1)

(2)

(3)

Al:Al:C,Va

(1)

(2)

(3)

Al:Fe:C,Va

(1)

(2)

(3)

Fe:Al:C,Va

(1)

(2)

(3)

Fe:Fe:C,Va

. (20.38)

Table 20.9 Calculated thermodynamic parameters required by the (Fe, Al)

(Fe, Al)

(C, Va)

-type three-sublattice

model

Structure Structure Magnetism Calculated lattice Observed lattice Calculated formation

symbol parameter (nm) parameter (nm) enthalpy in the ground state

(kJ/mol of compound)

AlC E2

Paramagnetic 0.3677 − −128.5

Ferromagnetic 0.3677 0.3781 −139.5

FeC E2

Paramagnetic 0.3890 − +190.5

Al L1

Paramagnetic 0.3502 − −35.2

FeAl

Paramagnetic 0.3734 − −67.6

C − Paramagnetic 0.3645 − +88.4

C − Paramagnetic 0.4057 − +160.5

Calculation of the Thermodynamic Properties

of the κ Phase

The thermodynamic parameters required by the model

in the (Fe, Al)

(Fe, Al)

(C, Va)

form are evaluated us-

ing ﬁrst-principles calculations and the results are listed

in Table 20.9. The calculated values denote the forma-

tion enthalpies based on the stable structure of the pure

element in the ground state. The ferromagnetic state of

the κ phase is calculated to be almost 10 kJ/mol more

stable than its paramagnetic state, and the magnetic mo-

ment of the phase was calculated to be 3.05 μB. Besides

these cohesive energies for the stoichiometric com-

ponents, the interactions between atoms on the same

sublattice are deﬁned in the same way as for the thermo-

dynamic parameters, and these interaction parameters,

as well as the entropy term of the formation energy, are

estimated using the experimental phase boundaries.

Electronic Structure and Phase Stability

of the κ Phase

As shown in Fig. 20.20, a crystallographic similarity

exists between the Perovskite carbide κ and the Fe

Al–

structure, i. e., a C atom is placed in the center of

an octahedron composed of six Fe atoms occupying the

face-centered positions in the L1

structure. The actual

calculated equilibrium lattice constant of the Fe

Al–

structure is 0.3502 nm, while that of the κ phase is

0.3677 nm, which correspond well with the experimen-

tal results of Palm and Inden [20.21]. This fact implies

that occupation by the C atoms in the octahedral inter-

stitial sites causes an expansion of the L1

lattice. Since

the calculated enthalpy of formation of the κ phase

( −27.9kJ/mol of atoms) is much lower than that of the

Al–L1

structure (−8.8kJ/mol of atoms), it is con-

cluded that the interstitial C atoms enhance the stability

of the L1

structure. Thus, the role of the C atoms will

be discussed in the context of their electronic structure.

Part E 20.3

1082 Part E Modeling and Simulation Methods

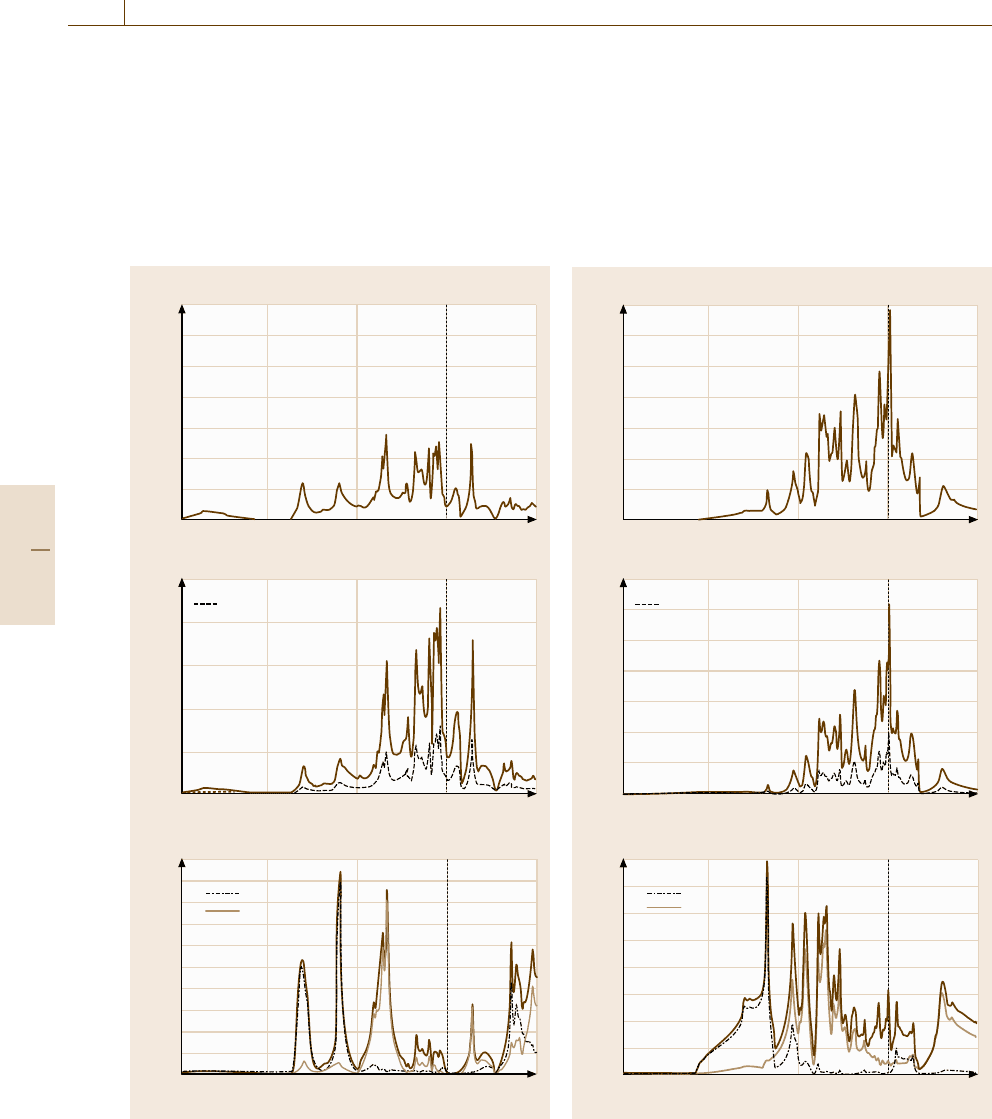
Figures 20.21 and 20.22 show the total density of

states (total DOS) and the angular-momentum-resolved

density of state for each element (p-DOS)forthe

AlC–E2

(κ)andFe

Al–L1

structures, respec-

tively. The term E

denotes the Fermi energy, and no

electrons occupy electronic states above this energy

level. In both structures, the DOS mainly consist of the

contribution from the Fe d-electrons. However, while

AlC-E2

0.16

0.12

0.08

0.04

–15 –10 –5

–15 –10 –5 0 5

AlC-E2

a) Total DOS

b) p-DOS (Fe)

c) p-DOS (Al)

(eV)

d-xy

Fig. 20.21 (a) Total density of states, and angular-

momentum-resolved density of states for: (b) Fe and (c) Al

for the Fe

AlC–E2

(κ) structure

observing these diagrams, we noticed a marked differ-

ence between these two structures, in that the Fermi

level is located near the peak of the total DOS for the

Al–L1

structure, but decreases in a region with

a very low DOS in the Fe

AlC–E2

structure. This fact

indicates that from an energetic point of view, the sta-

ble E2

structure of the κ phase is highly preferred,

compared with the Fe

Al–L1

structure.

Al-L1

0.3

0.2

0.1

–15 –10 –5

–15 –10 –5 0 5

AlC-E2

a) Total DOS

b) p-DOS (Fe)

c) p-DOS (Al)

(eV)

d-xy

Fig. 20.22 (a) Total density of states, and angular-

momentum-resolved density of states for: (b) Fe and (c) Al

for the Fe

Al–L1

structure

Part E 20.3

The CALPHAD Method 20.3 Prediction of Thermodynamic Properties of Compound Phases with First-principles Calculations 1083

Figures 20.23aand20.23b show the calculated

electron charge density plots of the Fe

AlC–E2

(κ)

and Fe

Al–L1

structures in the (00

) plane, where

the contour lines correspond to an electron density of

100 e/nm

. The Fe atoms can be seen in the middle of

the horizontal and vertical axes, while the C atoms are

located in the center of the Fig. 20.23a. From these con-

a) Fe

AlC-E2

b) Fe

Al-L1

Fig. 20.23a,b Calculated electron charge density plots of:

(a) the Fe

AlC–E2

(κ)and(b) the Fe

Al–L1

structures

in the (001/2) plane

tour plots, it can be seen that bonding between the Fe

and C atoms occurs in the Fe

AlC–E2

structure, since

a ﬁnite charge density between these atoms can be ob-

served. This interaction between the atoms enhances the

energetic stability of the Fe

AlC–E2

structure.

Comparison of the Calculated Phase Equilibria

with the Experimental Data

The calculated Fe

−

C ternary phase diagrams are

showninFig.20.24 for temperatures, T = 800, 1000,

and 1200

◦

C. The enlarged portion of the isothermal

section diagrams is compared with the experimental

phase boundaries determined using X-ray diffraction

and metallographic observation [20.21]. From EPMA

measurements, they reported that the chemical compo-

sition of the κ phase shifted remarkably from its stoi-

chiometric composition. The homogeneity range of the

κ phase extends from Fe

2.9

1.1

0.7

to Fe

2.8

1.2

0.7

according to the calculations.

20.3.2 Thermodynamic Analysis

of the Co–Al–C and Ni–Al–C Systems

The microstructures of Ni-based superalloys contain the

Al–L1

phase, which shows an anomalous ﬂow–

stress dependence on temperature [20.22]. In addition,

because they exhibit very high melting temperatures

and have good resistance to oxidation, alloys with com-

plex phase structures containing the NiAl–B2, fcc-Ni,

and Ni

Al–L1

phases have been investigated for tech-

nological applications. On the other hand, it is difﬁcult

to produce Co

−

Al-based superalloys with a microstruc-

ture consisting of fcc-Ni and Ni

Al–L1

, because of

the absence of a stable strengthening L1

phase in

the Co

−

Al binary system. However, the addition of

carbon to this alloy stabilizes the formation of the

Perovskite type carbide (E2

) with the composition,

AlC (κ phase), as seen in Fig. 20.18, and this carbide

is anticipated to form a ﬁne coherent microstructure in

a Co-based solid solution. Then the entire phase equi-

libriaoftheCo

−

C ternary system is attempted to

be clariﬁed by coupling the CALPHAD and ab ini-

tio calculations. The same procedure is applied to the

−

C system, and the results are compared to the

−

C system.

Calculation of the Co–Al–C Phase Diagram

The same thermodynamic model as (Fe, Al)

(Fe, Al)

(C, Va)

is applied to the Co

−

CandNi

−

based κ phase, and the parameters necessary for this

model are evaluated using ﬁrst-principles calculations,

Part E 20.3

1084 Part E Modeling and Simulation Methods

a) 800 °C

20 40 60 80Fe Al

FeAl

C content

(mol. %)

20 40

mol. % C

mol. % Al

Palm, Inden

+ (C)

b) 1000 °C

20 40 60 80Fe Al

FeAl

C content

(mol. %)

20 40

mol. % C

mol. % Al

Al content (mol. %)

c) 1200 °C

20 40 60 80Fe Al

C content

(mol. %)

mol. % C

mol. % Al

Palm, Inden

Al content (mol. %)

+ (C)

γ + (C)

γ +

+ + (C)

Palm, Inden

+ (C)

γ + (C)

γ +

+ + (C)

Fig. 20.24a–c Isothermal section diagram calculated

at:

(a) 800

◦

C, (b) 1000

◦

C, and (c) 1200

◦

C with an

enlarged portion on the Fe-rich side

Part E 20.3

The CALPHAD Method 20.3 Prediction of Thermodynamic Properties of Compound Phases with First-principles Calculations 1085

Table 20.10 The calculated thermodynamic parameters required by the (M, Al)

(M, Al)

(C, Va)

-type three sublattice

model

Structure Structure Calculated lattice Observed lattice Calculated formation

symbol parameter (nm) parameter (nm) enthalpy in the ground state

(kJ/mol of compound)

AlC E2

0.3675 0.3700 −179.0

CoC E2

0.3909 − +113.5

Al L1

0.3515 − −79.6

CoAl

0.3726 − −90.4

C − 0.3621 − +98.0

C − 0.4057 − +160.5

AlC E2

0.3713 −141.0

NiC E2

0.3905 +64.5

Al L1

0.3504 0.3572 −169.5

NiAl

0.3774 −91.6

C − 0.3645 +61.0

as listed in Table 20.10. The calculated Co

−

ternary phase diagrams are shown in Fig. 20.25 for

temperatures of 900

◦

C, 1100

◦

C, and 1300

◦

C. The

enlarged portion of the isothermal section diagrams

at 1100

◦

C was compared with the experimental

data [20.21].

The κ phase only appears at the stoichiometric com-

position in our results, while a small homogeneity range

is exhibited by this phase in the experimental phase

diagrams. This aspect is closely related to the large,

positive formation energies in the metastable ordered

structures, such as Al

CoC and Al

C. As the formation

energy of Co

AlC shows an extremely large negative

value when compared to these structures, the κ phase

only forms at the stoichiometric position. The homo-

geneity can be expressed by introducing interaction

parameters between unlike atoms in the same sublattice.

However, this treatment is not applied in the present

analysis, because the experimental phase boundaries of

the κ phase are still uncertain.

The calculated vertical section diagrams at constant

10 mol % C and 30 mol % Al are shown in Fig. 20.26b.

The calculated values agree well with the experimen-

tal results, and hence, the new type of approach based

on the incorporation of the CALPHAD method into ab

initio calculations has proven to be applicable to phase

diagram calculations for higher-order systems.

Calculation of the Ni–Al–C Phase Diagram

In the Ni

−

C system, on the other hand, it has been

experimentally veriﬁed that the κ phase does not appear

in the vicinity of the stoichiometric composition. Fig-

ures 20.27a–c show the calculated isothermal section

diagrams at 900, 1000, and 1300

◦

C, respectively.

Phase Separation of the κ Phase

in the Co–Ni–Al–C Quaternary System

According to the ﬁrst-principles calculations, there was

a large difference in the phase stability between the

Al–L1

and Ni

Al–L1

phases, compared to the

difference between the Ni

AlC–E2

and Co

AlC–E2

phases. In such an energetic situation, a two-phase sep-

aration should occur, depending on the difference in

the formation energies of the compounds, given by the

following expression

ΔG =

AlC

−

AlC

(20.39)

This miscibility gap originates in the energy differ-

ence between the terminal compounds, and as the

absolute value of ΔG increases, then the critical

temperature of the miscibility gap increases. Such

a phase separation is often observed in some com-

plex carbonitrides or alloy semiconductor systems.

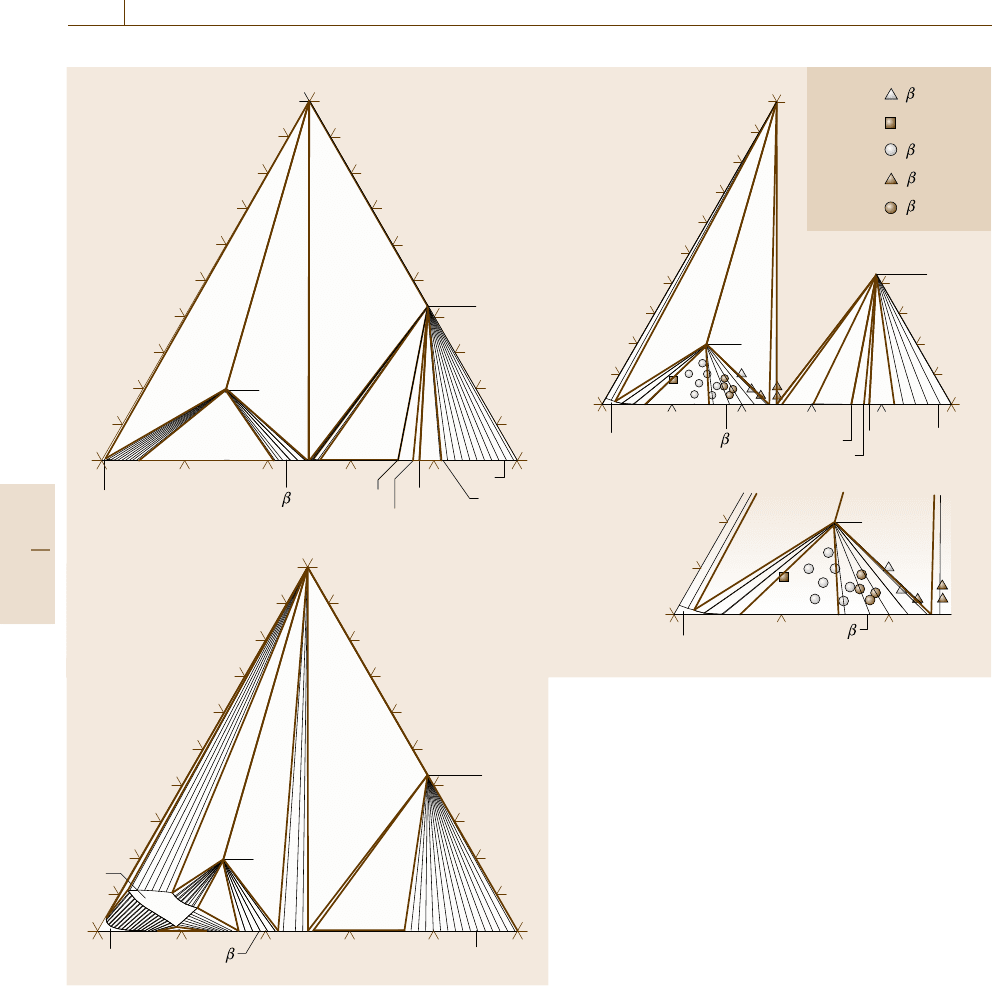
Figure 20.28 shows the calculation of a miscibility gap

in the Co

AlC

−

AlC

−

Al pseudoquater-

nary system at T =1000

◦

C. In this model calculation,

only the formation enthalpies of the stoichiometric com-

pounds are used, designated by the four vertices of the

composition square. One can see that a two-phase sep-

aration forms in the direction of the Co

AlC and Ni

diagonal. Therefore, a two-phase separation between

these terminal compounds will be involved in the phase

equilibria of the quaternary system.

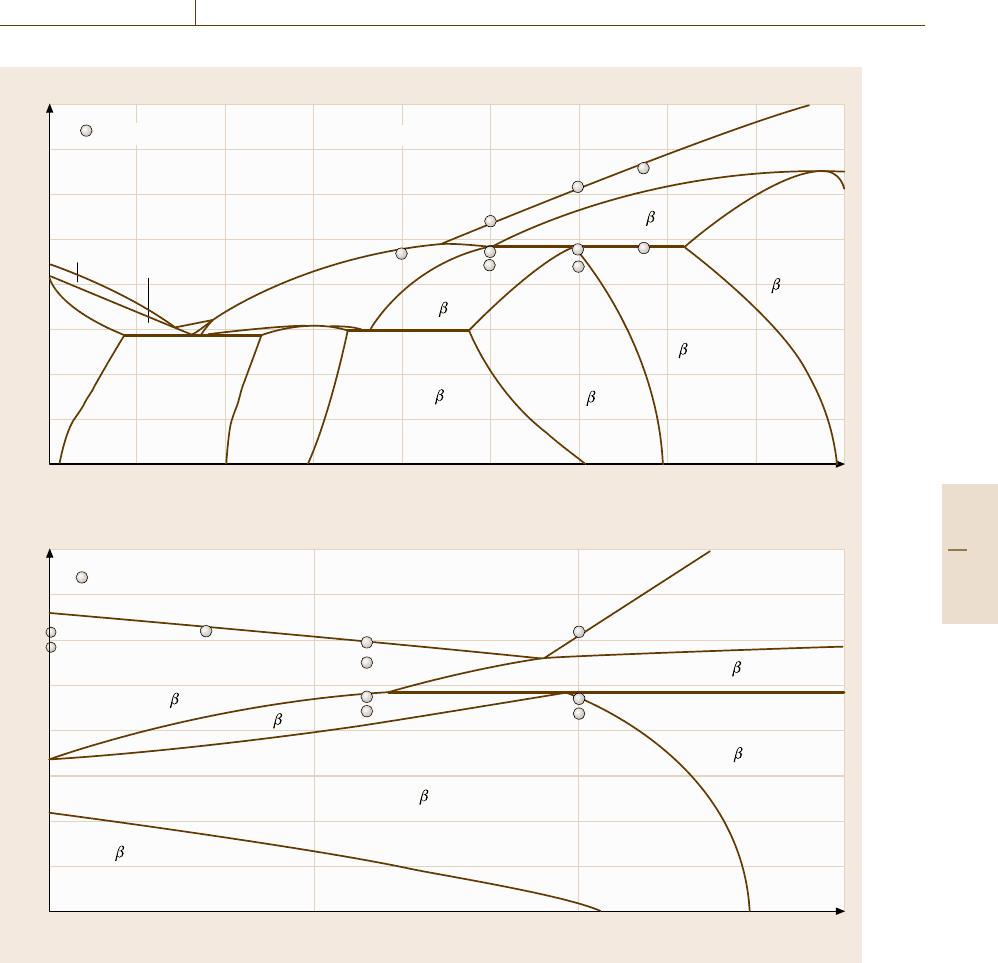
Using the thermodynamic description of the four

ternary systems that comprise the Co

−

C qua-

ternary system, a vertical section diagram is calculated

Part E 20.3

1086 Part E Modeling and Simulation Methods

a) 900 °C

20 40 60 80

Co Al

20 40

Co Al

b) 1100 °C

20 40 60 80Co Al

1300 °C

γ(Co)

C content

(mol. %)

20 40 60 80

AlL

Al4

CoAl

Al content (mol. %)

γ(Co)

C content

(mol. %)

Al content (mol. %)

γ(Co)

C content

(mol. %)

Al content

(mol. %)

Kimura

et al.

CoAl

Al (mol. %)

C (mol. %)

+ (C)

+ γ

at a constant C content of 4 mol %, and an Al content

of 23 mol %, as shown in Fig. 20.29. In this ﬁgure, the

term κ

denotes the Ni-based L1

structure, while the

Co-based Perovskite structure is represented by κ

.At

higher temperatures, the E2

structure forms a homo-

geneous solution, and this phase is designated as κ.

Fig. 20.25a–c Isothermal section diagram of the Co

−

C system calculated at: (a) 900

◦

C, (b) 1100

◦

C, and

◦

The κ phase gradually changes its character from the

AlC-based carbide to the Ni

Al-based intermetal-

lic compound with increasing Ni content in the alloy.

The precipitates decompose into almost stoichiomet-

ric Co

AlC and Ni

Al phases in the lower temperature

range.

Part E 20.3

The CALPHAD Method 20.3 Prediction of Thermodynamic Properties of Compound Phases with First-principles Calculations 1087

1700

1600

1500

1400

1300

1200

1100

1000

900

Al content (mol. %)

a) Temperature T (°C)

b) Temperature T (°C)

Co-Al-10 mol % C

90 mol. %

+ (C)

Kimura et al.

γ+L

+ (C)γ

+ +(C)

+L +(C)

L +(C)

+(C)

γ +

1700

1600

1500

1400

1300

1200

1100

1000

900

Co 1510

455 10152025303540

C content (mol. %)

Co-30 mol % Al-C

70 mol. %

Kimura et al.

γ +

L + (C)

+ + (C)

+L + (C)

Fig. 20.26a,b Calculated vertical section diagrams at constant (a) 10 mol % C and (b) 30 mol % Al

Part E 20.3