Бугай П.Т. Теорія помилок і спосіб найменших квадратів

Подождите немного. Документ загружается.

Середня квадратична помилка т, виміру кута при пер

шому положенні кола буде, очевидно, в -/~2 раз більша

від тн\

ту = У 2 ■ У тг,2 4- ~

Середня квадратична помилка т середнього арифметич

ного значення кута з вимірів при двох положеннях верти

кального кола дорівнюватиме:

m ^ 7 r = V m v2+m i г - (25 >7 >

Приклад 2. Визначити середню квадратичну помилку mh

перевищення між двома пікетами при нівелюванні з сере

дини і при одному встановленні інструмента, якщо середні

квадратичні помилки відліку по латі і установки по рівню

візирної осі нівеліра в горизонтальне положення дорівню

ють те і т„". Віддаль від нівеліра до рейки рівна сі.

Через те, що /я„ задають в міліметрах, a mv" — в секун

дах дуги, то для приведення помилок до одної міри вира

зимо /Яг," теж в міліметрах:

(25,8)

де р — кількість секунд в радіані.

Середня квадратична помилка відліку а по задній рейці

при сумісному діянні зазначених вище двох джерел поми

лок за формулою (25,5) дорівнюватиме:

а = ± У m e'2 + mv2

Таку саму помилку буде мати 1 відлік b по передній

рейці. Звідси середня квадратична помилка перевищення

дорівнює:

mh =таУ 2 = V2 (me2 + mvi). (25,9)

В конкретному випадку при тв = 2 мм, mv" = 3" і d = 5Q м

50000X3" А 7

mv 206 265 ’ ММ’

rrih=±Y (2,0)2 -Ь (0,7)- =±2,1 мм.

§ 26 ОЦІНКА ТОЧНОСТІ ПРИ СУМІСНОМУ ДІЯННІ

НА ВИМІРИ ВИПАДКОВИХ І СИСТЕМАТИЧНИХ

ДЖЕРЕЛ ПОМИЛОК

До цього часу, вивчаючи теорію помилок, ми брали до

уваги лише випадкові помилки вимірів. Щодо систематич

них помилок, то ми вважали, що всі джерела цих помилок

нам відомі, закони їх діяння вивчені і самі систематичні по

милки виключені з результатів вимірів. Але в дійсності це не

завжди так. Часто трапляються випадки, коли систематич

ний вплив того чи іншого фактора не можна вивчити нас

тільки, щоб звільнити від його впливу результати вимірів.

Отже, виникає питання, як оцінювати точність вимірів, коли

результати їх обтяжені не лише випадковими, а й можливи

ми систематичними помилками. Розглянемо окремі випадки.

1. Наявність в результатах вимірів постій-

и ої п о м и л к и. Нехай маємо ряд результатів Іи 12, In

рівноточних вимірів однієї величини X. Позначимо їх

істинні помилки через Aj, Д2, ... , А Припустимо далі, що

кожна з них складається з двох частин: випадкової помилки

Є; і ПОСТІЙНОЇ k, тобто

А, = є, \-k,

А., “ £9 "J -

.................

(26,1)

А,; = £/; -\-k.

Тоді можемо написати ряд таких рівнянь:

...

Х ~ 1 2- А3,

Х = 1п-Ьп,

або

X = lt- ei- k,

X - l 2—% - k , (26,2)

X - l n - Z n — k.

Підсумуємо ці рівняння і суму поділимо на п:

або, позначивши --через Х 0 і беручи до уваги четверту

властивість випадкових помилок,

1 іm Х„ = X + k. (26,3)

П -* ~

Отже, граничив значення Х 0 середнього арифметичного

з результатів вимірів при я->оо відрізнятиметься від істин

ного значення X на величину постійної помилки k.

Якщо постійна помилка k відома, то її можна вилучити

з результатів вимірів і одержати нові значення вимірюваної

величини:

яке від Л'0 буде відрізнятися на величину k.

Дамо тепер оцінки точності одних і тих же вимірів у

двох випадках—коли величина постійної помилки k відома

і вилучена і коли вона невідома. В першому випадку зна

ходимо найімовірніші помилки

Справді, беручи до уваги рівності (26,4), можемо написати,

що

Підставивши послідовно (26,4) і (26,11) в (26,6), одер

жимо:

що й треба було довести.

Таким чином, при наявності в результатах вимірів постій

ної помилки k середня квадратична помилка одного виміру

буде однакова незалежно від того, чи виключена вона з

вимірів, чи ні. Інакше кажучи, за збігом окремих результа

ті» вимірів однієї величини не можна судити про наявність

(26,4)

— hi k,

а за ними знайти і найімовірніше її значення

(26,5)

(26,6)

(26,7)

Так само і в другому випадку знаходимо

о/ = її - Х 0 (і = 1,2, .. . , п),

(26,8)

(26,9)

Але легко довести, що Оі'= Оі, а звідси й

т' = т. (26,10)

Х0' = Х 0 — k.

(26,11)

(26,12)

чи відсутність у них постійної помилки. Через те на вияв

лення і вилучення з вимірів цих помилок треба звертати

особливу увагу.

Знайдемо нарешті за істинними помилками (26,1) середню

квадратичну помилку тп\ для цього піднесемо рівності

(26,1) до квадрата, підсумуємо і суму поділимо на п:

Квадрат середньо! квадратичної помилки середнього

арифметичного Х 0 слід обчисляти за формулою

2. Наявність в результатах вимірів змінної

систематичної помилки одного виду. Нехай має

мо ряд результатів рівноточних вимірів однієї величини X.

Позначимо їх істинні помилки через Д; і припустимо, що

кожна з них складається з сумарної випадкової помилки

єі і змінної систематичної ПОМИЛКИ а,-, які походять з одного

джерела. В цьому випадку можемо записати:

Піднесемо обидві частини цих рівностей до квадрата, під

сумуємо результати і, поділивши суму на п, одержимо:

і м _ м + * + 2 *м .

I t п 11

Але

lim = — = 0,

п г

а тому при досить великому п

m2*=m,2 + k2,

(26,13)

де

(26,14)

де

(26,15)

Ді = єі + ои

Д2 “ £2 + а2>

(26,16)

Д п — Ч' .

і;л2] = И | [а2] , 2[ео]

п п п п

Але добутки єі а( як щодо величини, такі щодо знака мати

муть випадковий характер. Через те третій член правої час

тини останньої рівності порівняно з [першими двома буде

величиною досить малою, а тому ним можна знехтувати і

рівність (26,17) записати так:

1Д2І

або

/Ид2 = т е 2 + mz 2

1 mh ■= ± V т + т /1, (26,18)

тобто середня квадратична помилка одного ви

міру при сумісному діянні джерел випадко

вих помилок і одного джерела систематичних

дорівнює квадратному кореню з суми квад

ратів середніх квадратичних помилок випад

кового і систематичного впливу.

3. Наявність в результатах вимірів систе

матичних помилок декількох видів. Нехай дано

ряд результатів рівноточних вимірів однієї величини:

/] , / 2, . . . , In

з істинними помилками

кожна з яких складається з випадкової помилки е; і систе

матичної

Припустимо тепер, що помилки о; в свою чергу склада

ються з таких, наприклад, двох окремих видів систематич

них помилок о/ і а". При цій умові будемо мати:

Aj = £[-| Oj'+CTj",

Л2 = г2 + а2'-г а ./',

............................. (26,19)

А/г = + ая, Л-ап"■

Знайдемо середню квадратичну помилку т одного виміру

за істинними помилками А;, Для цього піднесемо рівності

(26,19) до квадрата, підсумуємо і результат поділимо на п\

m _ М , K 'J , к 21 , 2_[soj 2[гс") 2![„;<,"]

п п п п п 11 п ’ '

п . . . 2[го'] . 2 [so"]

При великому числі вимірів п величини — —- 1 —“

будуть відносно малі, а тому ними можна знехтувати. Але

2 .,

цього не можна сказати про величину . На практиці

можуть бути випадки, колі всі добутки о/о/' матимуть один

і той же знак. Через те в формулі (26,20) останній член в

правій частині може бути конечною величиною приблизно

одного порядку з першими членами. Отже, в остаточному

виді замість співвідношення (26,20) можна записати

/Яд2 = т.га+ т а'2-!-/геа» Ч ~ "0л° (26,21)

де члени

/По-3 + тУ- + 2-Ц~-- = (26,22)

виражають сумарний вплив систематичних помилок обох

видів.

Таким чином, при наявності в результатах вимірів де

кількох видів систематичних помилок, які походять від різ

них факторів, при оцінці точності необхідно враховувати і

члени виду

2 [“'«"Д 2К="1 2IVV,,1 (OR 9*^

п ’ п ’ п ’ ' ' ' І ‘

Практично для оцінки точності в цьому випадку необ

хідно для кожного виміру знайти сумарну систематичну

помилку

- / І - rr І "г '

Ji — 'Г *т

потім знайти середню квадратичну помилку т3 сумарного

систематичного впливу

т'- = + m S + . . . + 2 Ц р 4 2 ^ р + ... (26,24)

і лише тоді обчисляти загальну середню квадратичну по

милку одного виміру за формулою

гпь2 = ті2 + та-. (26,25)

Тут необхідно зауважити, що ряди істинних помилок

(26,1), (26,16), (26,19) у всіх трьох розглянутих випадках

не будуть підлягати нормальному закону розподілу, а через

те до них не можна застосувати формулу

Агран = З М1±

для визначення граничної помилки. І взагалі при встанов

ленні методики повторних вимірів будь-якої величини, об

робці і оцінці їх точності необхідно в кожному окремому

конкретному випадку вивчити закон, за яким те чи інше

можливе джерело систематичної помилки може впливати на

виміри. Лише при цій умові можна одержати надійні резуль

тати і зробити вірні висновки з них.

§ 27. ОБРОБКА РЕЗУЛЬТАТІВ РІВНОТОЧНИХ ВИМІРІВ

При обробці ряду результатів рівноточних вимірів однієї

величини необхідно: 1) визначити найбільш надійне, або

найімовірніше значення вимірюваної величини, 2) знайти

середню квадратичну помилку т одного виміру, яка харак

теризує точність вимірів при даних умовах, і 3) визначити

середню квадратичну помилку остаточного значення, одер

жаного в результаті обробки.

За найімовірніше значення вимірюваної величини з ряду

рівноточних вимірів приймають середнє арифметичне, яке

обчислюють за формулою (15,1):

Але ще краще, особливо при великому числі вимірів п,

знаходити його за допомогою наближеного заокругленого

значення /0 і лишків г за формулою (15,13):

Середня квадратична помилка т одного виміру визна

чається за формулою Бесселя:

з контролем обчислення за формулою Петерса:

Для контролю обчислень [ S31 виведемо такі формули.

Запишемо очевидну рівність

|8о] = 8j (Zj L„) + 53(/2 —Z.0) -1- ... +3„(/„ - £ 0)= [/5| —£0 [S].

Але [§] — 0. Звідси

Якщо середнє арифметичне обчислюють за формулою

(15,13), тоді застосовують дві контрольні формули, які ви

водяться так:

[S8J = [/З].

(27,1)

1) ' \1'>] — °](/() + гі) + °2(^о + гг) + - ■ • + (/0 + £л ) =

■або, беручи до уваги (27,1),

[Зо]= [оє]. (27,2)

2) Запишемо такі дві системи рівиостей:

/і /,0 = 5], Zj —/0 = Є(,

І'І ^2

In /-о — ®п , ^л /0 ^л ,

де Z-o - середнє арифметичне з результатів вимірів /г,

/0 — наближене заокруглене значення вимірюваної величини,

5,- — ЛИШКИ.

Віднімаючи почленно від перших рівностей другі, одер

жимо:

°1 = /о Sj,

8^ ^ - L« t £2: (27’з>

Од Iq L{j ~\~£n *

Піднесемо ці рівності до квадрата і результати підсу

муємо:

І З2] = И + П {І* + V - 2 / 0L0> +2 [є] {/0 - L 0). (27,4)

г.і

Але /,,= Л0 — Підставивши це значення в (27,4), буде

мо мати:

І°2] - Iе2] + «{(/.0- И )2 + I 02-2 Z 0 (Z.0—й )[ +

+ 2[e]{(l0- M ) - Z 0},

або, розкривши дужки, після зведення подібних членів

одержимо другу згадану вище контрольну формулу:

о- = є-

(27,5)

Середня квадратична помилка М середнього арифметич

ного визначається за формулою (20,14):

УИ= 4 - і /

~ У піп-

Числові приклади обробки результатів рівноточних ви

мірів див. в § 21.

§ 28 ЗАДАЧІ НА ЗАСТОСУВАННІ ТЕОРІЇ ПОМИЛОК '

і РІВНОТОЧНИХ ВИМІРІВ У ГЕОДЕЗИЧНІЙ ПРАКТИЦІ

-у Задача /, Чому дорівнюватиме середня квадратична по-,

шлка ота суми кутів теодолітного гірлігона па п точок, якщо

<бр:едия квадратична помилка -виміру одного кута тл =30"?

Відповідь знаходимо за формулою

т ^± 3 0 "У ¥. . - .

Задача 2. Середня квадратична помилка суми кутів од-

юдю трикутника гпц *= ± 3",5. Знайти середню ' квадратичну

юмилку іпа одного виміру кута. ' . !.

За формулою (19,7) знаходимо

У ' ■ : ' - ’/ ■' ■ J

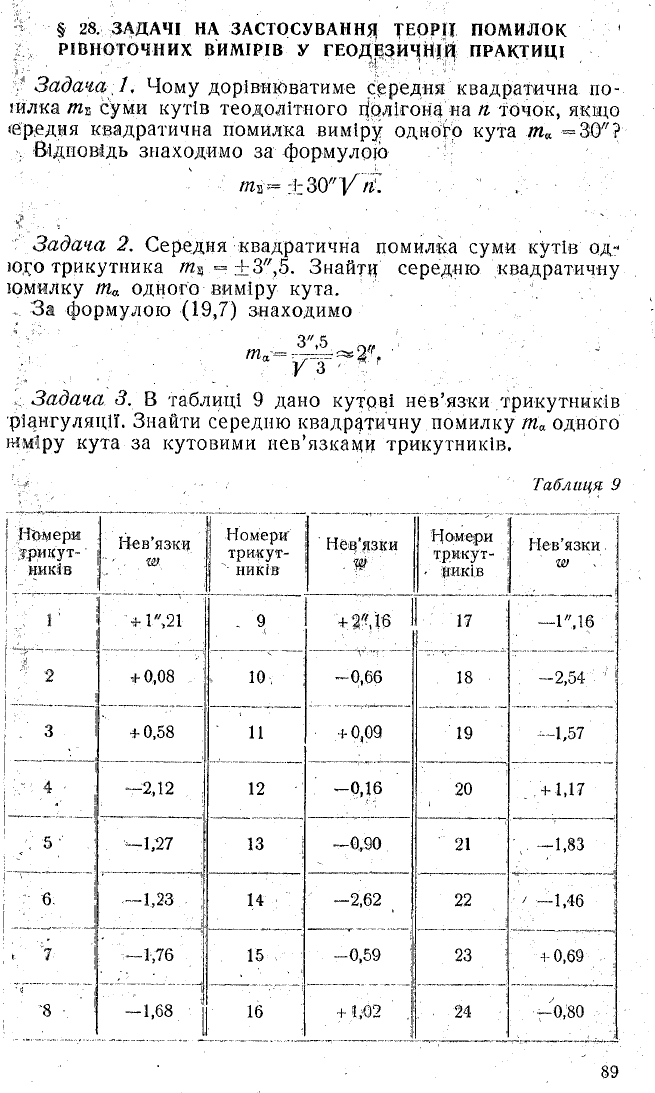
, Задача 3. В таблиці 9 дано кутрві нев’язки трикутників

рідигуляції. Знайти середню квадратичну помилку мл одного

ншіру кута за кутовими нев’язками трикутників.

Таблиця 9

і ІТомєря

грикут-'

1 НИКІВ

1 ... "■

Нев’язкч

- • да.

Номери'

трикут-

х ників

' Нсн’язки

Номери

трмкут-

• ЦИКІ.В

Нев’язки.

w .

1 ’

+ 1*721

. 9

+ 2,?Д6

—Г',16

+ 0,08

10, -0,66

; -2,54 -

+ 0,58

+ 0,09

1,57

.> 4 .

*-2,12 12

-0 Д 6

+1,17

— 1,27

із !

-0,90

21 — 1,83

—1,23 -

-2,62

' — 1,46

» і

—1,76

15 -

-0,59

+ 0,69 - ;

'8 •. '

—1,68

+ 1,02 ' .

• 24

-0,80

Нев’язки трикутників w можна розглядати як істинні

помилки сум кутів трикутників. Середню квадратичну по

милку гїі'і, суми кутів одного трикутника знаходимо за фор

мулою (16,5):

Підставивши сюди замість т; її значення (28,1), мати

мемо

Ця формула відома під назвою формули Ферреро. За

даними таблиці т а=±0",81.

Задача 4. На даній лінії сталева стрічка довжиною І

уклалася п разів, отже, довжина лінії d = nl. Знайти середню

квадратичну помилку та в довжині лінії, якщо середня

квадратична помилка одного відкладання стрічки дорівнює т.

Загальну довжину лінії можна розглядати як суму п

рівноточних відкладань вимірювального приладу. Отже, за

формулою (19,5)

Для даного вимірювального приладу і при даних умовах

При d= 1 одержимо md = щ тобто величина jx є середня

квадратична помилка виміру, що припадає на одиницю дов

жини. З формул (28,5) і (28,6) видно, що випадкові помилки

при вимірах ліній зростають прямо пропорціонально квад

ратному кореню з довжини лінії.

(28,1)

Але на основі відповіді попередньої задачі

(28,2)

(28,3)

та — ± т у п.

Але згідно з умовою задачі ^ =

чення п в (28,4), одержимо:

(28,4)

Підставивши це зна-

md = ± іі Vd.

(28,6)