Бугай П.Т. Теорія помилок і спосіб найменших квадратів
Подождите немного. Документ загружается.


[ у K + [ y K + - - - + [ y K +™ 2=0,
[у ]* 1 + [ у ] ^ 2 + - + [ ~ ] ^ + ® , = 0
на неозначені поки що множники qu q2, ..., Яг і добутки до
дамо до функції (87,7). Після зведення подібних членів по
корелатах одержимо:
/ Ч [ у ] ^ + [ у ] ^ + - + [ у ] ^ + [ | |}*х+
..................................................................................
.............
(87,8)
+ { [ у \<h+[j-]v*+ - + [ j ]qr + I J 1 K +
+fo + Wiqr\-W2<l2+ — +'Wr Яг + / « 8«+/fS SP+ Л 8Ї '
Користуючись неозначеністю множників q\, q2. ...» Qr> під
беремо їх аначення так, щоб вирази у фігурних дужках до
рівнювали нулю:
[ f ] ?, + [ f b + . . . + [ f ] ?, + | f ] = o ,
[ ? М “]*+»+[£1*+І?И
.................................................................................... (87.9)
! у к і + [ т г 1 ? ! + - + [ у ] ? ' + І7 '1 — °-
Тоді функція (87,8) набере такого вигляду:
f=zfQ+'wlqy+'w2q2+...+Wr q, +
+ / І 8а + / Р8 р + /,8 Т. (87,10)
Візьмемо тепер до уваги, що вільні члени wuw2,.. . , да„
по-перше, будуть функціями не лише результатів безпосеред
ніх вимірів, а й вихідних даних а, [3, y, тобто
чеі^щ (х/, х2, ... , х п', а, р, y),
w2=w2 (*/, х2, ... , Хп, а, р, Y), (87,11)
W r = W r(x і,Х./, ... , Хп, а, р, f),

і, по-друге, ці функції можуть бути складними. Отже, функцію
(87,10) доцільно представити в такому більш простому л і
нійному виді:
/ - { ( & ) .* + ( £ ? ) / ■ + ■ • • + № + М 8* '.+
+ { ( £ 7 ) / ' + ( 5 7 ' : ) , * + - + ( з ? , ) , » ' + f , , : І ;"с'=
+ W & ).,,+ ( & ) .ft+ ~ + (fc 9 .* +/*'„ }**'•+ <87’І2)
+ { ( т ) / . + ( т г ) л + - - - + ( Ї г ) „ » '+ Л 18“ +
+ !(*<>т).', , + ( ж ) " ' ? г + - + (t f ) / 7 , + л ! 8р +
+1 ($ М £ ).* +“+&)Л +''}*+'»
де часткові похідні можуть бути обчислені за наближеними
значеннями аргументів (кути, наприклад, можна взяти зао
круглені до десятків секунд), а
f х/ ~ dJtTT' * fo= f{xit> ^20 > ••• > Хп0 > а0- Ро> To)= COnst'
Якщо введемо позначення
....................................................................................................... (87,13)
і = ( ж ) 09і+ ( ж ) 0<72+---+ (^w)0gr + / р * (87,14)
< ?/ / д д а , \ . / d w , \ , . t d w r \ , ,
^ ( ^ г ) 0^ + Ь г ) / 2 + - + ( - * ) „ * ' + Л *
тоді формулу (87,12) можна записати в такому скорочено
му виді:

Маючи часткові похідні (87,13) і (87,14), ми можемо за
відомою з теорії помилок формулою написати такий вираз
для визначення середньої квадратичної помилки функції
\87,15) незалежних аргументів:
Легко ПОМІТИТИ, ЩО В цій формулі коефіцієнт При |А3
гобто він дорівнює оберненій величині ваги функції врівно
важених величин без врахування помилок вихідних даних, і
його можна обчислити в схемі Гаусса звичайним шляхом.
Отже, порядок обчислення середньої квадратичної помилки
функції з врахуванням помилок вихідних даних при врівно
важенні умовних вимірів буде такий.
1. Складають умовні рівняння
2. Складають нормальні рівняння перехідних корелат
(87,9). Розв’язуючи їх, знаходять перехідні корелати qit q2,
..., qr і обернену величину ваги даної функції за формулою
3. Розкладають у лінійні рядки вільні члени умовних рів
нянь за вихідними даними і одержують:
л 18лг1+ а 28л:2--|-..."|-яя Ьх„ -f®Y'-=0,
&і8л:г |-&28х2Н-... І-Ь„ Ьх„ 0,
r]bxl \-r2bx2 \~...~\-rn Ьхп +wr 0.
(87,17)
dw 1JS ддаїїа і dw.

■ d w , d w , і d w .
*>*=*>«>+ -df o a - ° ?+ d7 °‘>
(Зда, йге/, й®,
■Wr йа+ ~ду 5 р 4 — ^ - s Y -
4. Обчислюють числові значення часткових похідних (87,14)
загової функції за вихідними даними.
5. Визначають середню квадратичну помилку функції врів
-юважених величин з врахуванням помилок вихідних даних
за формулою
mf 2==/ ^ + ( ї ) т * + ® Щ 2 + (<|) оті *• (87*18)
§ 88. ВИЗНАЧЕННЯ СЕРЕДНЬОЇ
КВАДРАТИЧНОЇ ПОМИЛКИ ФУНКЦІЇ ВРІВНОВАЖЕНИХ ВЕЛИЧИН
З ВРАХУВАННЯМ ПОМИЛОК ВИХІДНИХ ДАНИХ
ПРИ ВРІВНОВАЖЕННІ ПОСЕРЕДНІХ ВИМІРІВ
Нехай дано вагову функцію від t невідомих у такому
лінійному виді:
/?= / 1* + / 8y-h/sz + ...+ //« , (88,1)
де / і, / 2, /з. . ft — сталі величини, а х, у, z , ... , а — не
відомі, що входять у рівняння помилок
а ^ + Ь ^ + с ^ + . .. + txu-\- ll= v i,
a2x+b2y+c2z (88,2)
anx+bny-{-cnz+...+ t„u-\-l„—v„.
У цих рівняннях ВІЛЬНІ члени ІІ, І2, ■ • ■, In обчислюються
через результати безпосередніх вимірів L\, Ь2, . .., Ьп та ви
хідні дані, наприклад, а, р, т- У загальному виді вільні
члени можна записати так:
а> Р* *і)>
/2==<?2(^*» а> Т).
...................................... (88,3)
Р» т)"

Д ля визначення середньої квадратичної помилки функції
(88,1) ми повинні виразити її, в першу чергу, через вільні
члени /і, і2, .... Іп, а потім виключити і їх, виразивши через
безпосередньо виміряні величини L], Ь2, ..., Ln і вихідні дані
«, {З, Y, і, нарешті, знайти середню квадратичну помилку за
відомою загальною формулою
Як відомо, при врівноваженні посередніх вимірів «евідо
т х, у, ..., и визначаються з такої системи нормальних
рівнянь
\paa\x-\-\pab)y-\-...-\-\pat)u-\-\pal\— Q,
\pab]x-\-\pbb)y+...+\pbt}u+\pbl\=Q ,
.............................................................................. (88,5)
\pat\x+\pbt\y+...-\-\ptt\u+lptt\=Q.
Д ля виключення з функції (88,1) невідомих х, у, .... и
помножимо (нормальні рівняння (88,5) на неозначені множ
ники qu q2, qn і добутки додамо до функції (88,!). П ід
бираючи неозначені множники так, щоб
[paa)qi+\pab\q2+ ...+ \ p a t]q t + / і= 0 ,
\pab\ql-\-\pbb)qi-\-...+\pbt\qt + / 2= 0 ,
........................
..
................................
(88,6)
\pat\4i+\pbt\q2-\-...+\ptt]qt + ft = 0 ,
ми одержимо вираз функції (88,1) в такому виді:
р=:\Р<іІ]чА-\РЩ Ч2+-‘+\рЩ qt ■ (88,7)
Виключимо тепер і вільні члени рівнянь помилок, замі
нивши їх безпосередньо виміряними величинами і вихідними
даними. Д ля цього перетворимо спочатку рівняння (88,7).
Напишемо ряд рівнянь
\p al]= p1a 1l1+ p 2a2l2-\-...-\-pn ап Іп ,
[рЬ І]=р іЬї11-\-рфги + ..,-\ -р ІІ bn In .
\ptl\— Р\t\l\~\~P2^4гЛ~■ ■ -^Pn tn In -
Помноживши їх відповідно на qlt q2, . . ., qn і підсумував-

и добутки по стовпчиках, одержимо замість (88,7) такий
лраз:
Для скорочення дальших записів введемо такі позначення:
З цими позначеннями функцію (88,7) можна записати
ак:
Величини є і — сталі, що видно з рівнянь (88,9). Щоб за-
(їиити в (88,10) вільні члени рівнянь помилок 1\, І2, /„
безпосередньо виміряними величинами Li, L2, .... Ln і ви
ідними даними а, (з, у, необхідно, очевидно, (88,3) підстави-
и в (88,10). Але при цьому треба мати на увазі, що функції
88,3) можуть бути складними, і для спрощення обчислень
х доцільно спочатку привести до лінійного виду, /(ля цього
.ізьмемо систему наближених зчцічень безпосередньо вимі-
иших величин і вихідних даних
F M P ia lqv \-plblqr \-...-\-pltlqt ) / j-f
+ {РгагЧ\ Л- Р-іЬгЧг-\-...-\гР‘2?і<їі ) /2+
(88,8)
+ (/> « ап qx-\-pn Ьп qr \-...-\-pn t„ qt )l„.
PiOlqi+Plblqr [--+P^i4t =*i,
р><ЧЯіУрЬЛг\---A-P-ittft = e 2t
(88,9)
Pn Gn lJ i (~Pn &n ^2 'l—•••'! Pn ЯI r— ~‘l •
(88,10)
поправок до них
(^i)> (^-a)» •••> (^n)t
(a), (P), (T).
(88,11)
гак що
(88,12)
a— « 0-Н а)>
Р—Po-HP^
Т=Т0“ИТ)-

а, р, ї ) = ? ю + ? 'іі(£і)+<Р *!«(<»)+? 'з (Р )+
+ 'Р 'іт(т),
/2= cp2(Z.2l а, р, т ) = ? г о + ? и ( ^ ) + Т & (< *)+ ? 'гріР)+
+?2Т'( ї) ,
.............................................................................................. (88,14)
— ®Я (•£« , а , Р, 7)= ? л 0 + ? niXJ-n )_Ь :Рл!і,(а^_1~''РлЗ'(Р)-|-
+ < Р я Л ї).
З цими значеннями величин /г- можемо функцію (88,10)
записати так:
/ • '= E i / , - f + . .. - |- Є я / л =
= sicp,i/-(^i^-b2a?/^ ? 'nL{Ln ) +
4-{il® 'lc+ S2tp ? Ла}(а )~Ь
+ { Є1СР/І?+ S2?,2 ?+ ---+£/l ? л р}(Р)+ (88,15)
+ { г1?,ІТ + Є2 ? Ч + - - - + 3Л V лт}(т) +
+ г 1 ? Ю + г 2 ?2оН _ - " + є л ? л 0 -
Введемо позначення
Xj^Sjcp’ii, Х2= є2®'2і , , Х „ = є л (р-лі,
Л ~ e,cp/|Ct-|-s2cp,2a-]-...-)-s„ ф ла>
5 = 6 ^ *ір —J—є2ср 2p - j - . српр, (88,16)
С — Sjtf 'і1- | -2 2'Р ,2т+ . . . + £л Т'лт,
^ о— г
1
(Р ю + є
2
?
20
+ - ” + єл ?'лО.
Тоді
F—F0-f-^](Z 1)-(-X2(Z._,)-)-...-|-Xn(Z.„)-|--
+ Л ( а ) + В ір ) + С ( Т),
де F0 — величина стала, яка на оцінку точності не впливає.
Тепер вже можна визначити середню квадратичну по
милку нашої вагової функції F, тому що вона виражена че
рез поправки (88,11), які мають ті ж самі помилки, що й
безпосередньо виміряні величини і вихідні дані.
Нехай середня квадратична помилка одиниці ваги буде
і1, а ри р2, , Рп — ваги виміряних величин. Тоді їх се
редні квадратичні помилки дорівнюватимуть:

Припустимо далі, що нам відомі і середні квадратичні
помилки та, т$, тл вихідних даних. Тоді, застосовуючи до
функції (88,17) загальну формулу (18,14) для визначення
передньої квадратичної помилки функції незалежних між
?обою аргументів, одержимо:
м 4 - Ы. JJ.2 1 І „21
Рх Г Р . г ^ рп р ~
+ Л 2ота3+ 5 2дар3+ С 2/гат2,
або
М Р *= [ ];А2_)_Л 2m a 2Jr B 2m? 2_j_C2mi 2, (88Д 8)
Як легко помітити, величина [ ^ | ц2 дорівнює квадрату се-
зедньої квадратичної помилки вагової функції без врахуван
ня помилок вихідних даних, тобто
XI-
т2р-
V-2= — ,
Рр
іе рр — вага функції врівноважених величин без врахуван-
ія помилок вихідних даних, яку можна знайти звичайним
ііляхом у схемі Гаусса— Д улітля при розв’язуванні нормаль-
іих рівнянь. Для визначення ж А, В, і С служать рівняння
88,16). Виключимо з них величини є,, є2, ... , є„ . Для цього
іізьмемо рівняння (88,9) і помножимо їх спочатку відповідно на
>1*', ?&', ... , Тла', потім на «Різ', <ргр'
........
'І. нарешті, на ®,т ',
>2/, ... , ? т'. Підсумовуючи кожен раз добутки по стовпчи-
:ах, будемо мати:
1/ю?« 'к Н -И ? * ']?2- Ь ••+[/>% ')qt =А,
Іраур ']?Н-[/Жрр ']? 2 + -+ И ? Р '\qt —В, (88,19)
\ р щ л ' І Я і + І Р Ь ' Ь
' ] ?
2
+ - + И ? т
] q t = С ,
[е перехідні коефіцієнти <7ь q2, ..., q t
визначаються з системи
іівнянь (88,6).
Опускаючи досить громіздкі перетворення, можна дове-
ти, що після підстановки в (88,19) значень перехідних кое-
пцієнтів у їх загальному виді для визначення величин А,
З і С одержимо такі загальні вирази:
А- - { р а а ] ^ ' Л Ь
_ M ^ L ^ ccpii >,2]—.,. ,
ІР сс.2]
'Н Й п г И 'Р Р '-Ч
Ui‘2\\pc^r.2\-..., (88,20)
[рсс.2у

Практично для обчислень за формулами (88,20) необхід
но при складанні таблиці коефіцієнтів рівнянь помилок разом
ч графами а. Ь, с, . . . ввести ще такі додаткові графи ъ'% ,
Таблиця 73
<?р'
V
V
V
V
? /1 0
і обчислити коефіцієнти
\Р<*9«']. [раь'І
і pb<?« 'J, [pb®s '], lpb?i'\,
..................................
...
(88,21)
\ pto.% І /> % '], \ pt^'\.
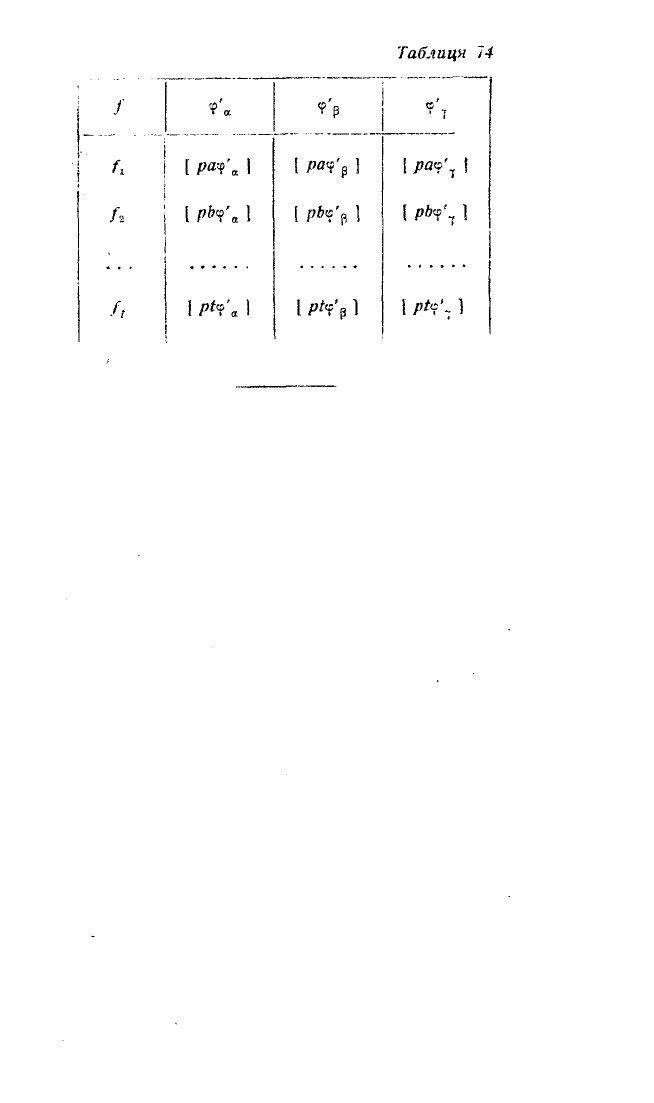
Якщо тепер до схеми ГауСса— Д улітля додати графи /,
'if <р'р, ф'7 і при розв’язуванні нормальних рівнянь виписува
ти в них величини, зазначені в таблиці 74, то, проробляючи
над ними ті ж операції, що й над коефіцієнтами нормальних
рівнянь, в останньому рядку схеми одержимо:
^ 1
в стовпчику / — величину — ,
Рр
в стовпчику < ? « величину А,
н стовпчику ®р'— величину В,
в стовпчику ? т '-~ величину С.
Підставляючи їх у формулу (88,18), знаходимо к ва др ат
середньої квадратичної помилки функції з врахуванням по
милок вихідних даних.
f
<6
*'т
■
и
[ рау'а 1
[ рач’9 1
1 рач\ 1
л 1 pbf'a 1
[ P h 'p 1
I Pb*\ 1
ft
1 Pty* 1 I 1
1 P*i‘- 1
