Бугай П.Т. Теорія помилок і спосіб найменших квадратів

Подождите немного. Документ загружается.

Піднесемо їх до квадрата і результати підсумуємо:

Ру-= [ЛЛ]-|-{[аа] ісп -1-[ab] *і2-Ь ” -+ [ аг]

4~{[ab\ *12-Ь ---+ [^ /'] 1С1/ -~ Н ^ ]}1С12~Ь

+ { [аг] г 11+[^Г] п12+--- \ [ГГ\ гАг[гК]}т.Хг-\-

+ { [ а'а'] ■*22+----H*V ]

-[-{[а 'Р '] тс21-)-[Р 'Р '] u23+

+ { [ a V ] іг21+ [р Ч '] u22+ ...-|--[xV ]

+ { И М " ] ^ 81+ [ Л ^ '> з 2 + - + [ ^ 1 ^ + [ А " Л ] } ^ 1 +

+ {[A " £ " К і+ [S "^ ] *32+-•, \-[B"H"\~3h-^-[B"A]}'r.32 +

+ {[Д "Я "]тг31+ ІЙ "Я "]1Гз2-Ь ..+ [Я "Я " ]ТСзй+ [Я "Л ]}х з ?І+

+ ([«* '] *21+ И '] K 2 3 + -+ M ^ f ) . 2icn+ '

-f([fta '] 1Г22~Ь---“Н ^ 'С ] TC20 . 2t 12-(-

-| -([ra ’] ■к2>-\ - [г $ , \т.22-]г . .. - \ - [ г х ' ] к . 2і ) , 2 щ г- \ -

+ ( M " ] ісзі+ ta fi"] *33+ - + [ ^ " ] яз*). 2теп +

+ ([М "] - з і + [ ^ ] « з 2 + - + [ ^ ' ] ^3ft) • 2т:12+ (81,13)

+ ( H W1 * 3 1 + m «3 2 + - + [ ^ " ] ^ 3Л) • 2іг, ,+

+ ( [ * ' > Г ] * 32+ - + К ^ " ] - 3ft) • 2 * гІ +

+ ( [ P ^ ,,l * 81-H P 'fi" ] ^32 + . . . + [Р,Я " ] ^зл) .2 тг224 -

+ ( М " ] тс31 + [х'5 "] *82+ . . .+ К Я " ] К№) . 2*2, +

+ [яЛ] *п+[&А] *12+ ...+ [гЛ ] iclr-j-

-)-[*'Л ] 1С21+ [Р 'Л ] ^22-f-- - ["с'А] 1С-><-|-

+ [Л "Л ] * 31 + [5"Л] * 3 2 + ---+ [Я "Л ] T.3h.

Для спрощення цього виразу візьмемо до уваги, що при

виключенні корелат з формули (81,10) ми підбирали неозна

чені множники тс так, що вирази у фігурних дуж ках форму

ли (81,10) дорівнюють нулю. Крім того, з теорії двогрупо-

вого методу врівноваження відомо, що

[аа'] = [ар'] = ... = И 'Н 0 ,

[йа'] = [&р'] = ... = [6т’]= 0 ,

[га']-[гр,]-»... = [гх']=0>

\аА'} = [аВ‘] = ... = [аН’] = 0,

[ЬА'\ = [ЬВ']~...~[ЬН'}= 0, (81,14)

[М '] = [ г £ [rtf']= 0,

[а 'Л "] = [а '£"] = ... = ] а 'tf"] = 0,

[р 'Л"] - [р '5"] - . . . = [р 'tf"] = 0,

[tV l"] = [x '5 "] = ... = [-'tf"] = 0.

Доведемо ще вірність таких співвідношень:

[ а Л " ] - [ а Я " ] - .. .-[ а / Л - 0,

[М "] = [65"] = ... = [Ш "]= 0 , (81,15)

[ г Л '] = [г £ Г] = . . . = [r t f "] = 0 .

Повторне перетворення коефіцієнтів умовних рівнянь дру

ої групи можна проводити за такими відомими формулами:

А і" = А і '4* а. і 'рп + р/ ,Рі2-К--~ЬХ І fPlN

. В і" = Z?v '-j- a, 2 3 ~І~Р ' 'Р22~\~ш"~\~Х < *р2/ (81,16)

я Н І а / 'Р / їІ^ Ь Р і fph2~\~ . І 'p h t,

е р — допоміжні корелати. Помножимо ці рівняння спо-

атку на відповідні щ, потім на bt і так далі і, нарешті, на

і і добутки підсумуємо:

[аА"\ = {ао.'\ Рц—{—[ар ] р !2 ( * * - ! [^х*] P\t~\-[aA ']=0,

\аВ"] = [аа'] р21-|-[ар ] P22-f- ----H wx,J 9у-\~\аВ'\ =0,

[atf ] — [ах ]рйі-(-[ар'] рлз—і-—— J P h t - \ - [d H ] = 0,

[ЬА*\ = [б»'] Pll+ [ ^ '] Pl2+ ...+ [ftx'] р, t+ [ b A '] =0. (81,17)

[ЬВ ] = [bd ] Р гі+ ^Р ] р22~\г--‘~\~[Ьі'] P2t-\~\bB') =0,

[ЬН”\ - [bx'[ Pft, + [ftp'] р;г24-...-|-[йх'] РМ\[ЬН'\ = 0,

всі вирази в круглих дужках теж дорівнюватимуть нулю, а

тому її можна записати в такому остаточному виді:

[Л Л ]+ [аА ] *П+[& Л ] *м+ ...+ [гЛ ) тгі-

-{-[а'А] [Р 'А] їс22+* --+['с,А-] *2Н

+ [ А 'гА ]1г81+ [ ^ л ]* 884 -...+ [Я "А і* »,

де неозначені множіники

*и. ^іг* ••• > тсі

*21 > *22’ ••• » 'K2t,

яаі, *32' ••• • *зл

визначаються відповідно з таких систем рівнянь:

[аа] іїц + [лй ] *і2+ ~ . + М * іг+ [аА ] =0,

[aft] *ц-{-[bb] *12—і- j- [^r ] яі /-Н^А] = 0, (81,18)

[ar] r.n+[br] « І2+ - . - + М я, r f[ r A ] = 0;

[a'a']*21+[a'P'] *22+...-|-[a V] *2,+ [a'A] =0,

[«ГЬі+[РГКН---.+Гх']* гЫР'Л] =0, (81,19)

[a V ] *2гН Р’х/] *22.+--- т IX х'] *2/‘-j-[x ,A] =0;

[Л"А"] г.;п+[А”В"} *8г+...+ [Л*7Г] *ЗЙ+[Л"А] =0,

[A"B”]^ + [B " B " ]^ + ...+ [B”H"] *зл+[Я"А] = 0, (81,20)

\А"Н"] ^31+ [5 "Я "]* 32ч -...+ [ Я " Я > ЗЛ+ 1 Я ,/Л] =0.

§ 82 ПЕРЕТВОРЕННЯ ЗАГАЛЬНОЇ ФОРМУЛИ

ДЛЯ ВИЗНАЧЕННЯ -----

Д л я обчислення величини р-- за формулою (81,17) необ

хідно знайти неозначені множники (81,8) та перетворені кое

фіцієнти другої і третьої груп. Але з теорії тригру

пового методу врівноваження відомо, що коефіцієнти умов

них рівнянь другої групи не перетворюються і систему рів

нянь (80,7) не розв’язують, тому що другі поправки v" об

числюються безпосередньо як функції вільних членів Wa, Wp,

wx. Щоб уникнути додаткових обчислень для визначення

величин PJ, формулу (81,17) необхідно відповідним чином

перетворити. Д ля цього звертаємось до формул:

та

-~і=А і -|-йі TZn -\-bl * , 2 Kir +

А і"т..АІ- ^ - В і і

Беручи до уваги правила розподілу умовних рівнянь на

групи, можемо (див. § 80) записати:

А, -|-а; *и+Ьі *12+ ...+ Г , - і ^ - = А , \ (82,2)

де [А]/ — сума вагових коефіцієнтів по /-й секції; п, — кіль

кість невідомих поправок, які входять в умовне рівняння пер

шої групи з номером / = 1, 2, 3, ... , г. Отже,

^ = А / + Д А ; '+ Л г% і+ ^ Ч 2 + -+ Я / " * з й) (82,3)

де введено позначення

ДА і '= а і і 7Г22_Ь---_Ьх і ы■ (82,4)

Порівняємо тепер (82,3) з (80,20):

ДА І ' = Лі і ,Рі2_Ь..._(_’С ' 'pit ,

ДВ і а і 'Р2і~\-$ і ,р22- К ,-~1- ’С і’рм,

Д Я і ' = а і 'рйі-|-[3 і /рЛ2 [ j 'рht-

Але, виражаючи допоміжні корелати р у функції вільних

членів рівнянь (80,21), (80,22) і (80,23), ми від формул

(80,20) перейшли до фо(рмул (80,30):

ДА і'= Рі [А ']1,'+<7, [А ']'*'+...+*/ [Aft,

АВі'=Рі [Я ']ї-ь ? і [ 5 '] ''+ -+ ^ m l

Д Я , \H'\l r-+ ti \Hft.

Так само, виражаючи неозначені множники іс21, гс22,...,*2<

у функції вільних членів рівнянь (81,19), ми можемо від

(82,4) перейти до формули

Д А , '= р, [A']!1—j— qt \А']1 (82,5)

Отже, зважаючи на (82,2) і (82,4),

( % ) = А , '- f -Л (82,6)

де

Л і "== А і '4 - Д А/'.

(82,7)

Таким чином, ми прийшли до висновку, що коефіцієнти ва

гової функції можна перетворювати так само, як і коефі

цієнти умовних рівнянь третьої групи, за формулами (82,2) і

(82,7). Підставивши вирази (82,6) часткових похідних ва

гової функції у формулу (82,1) , будемо мати:

-*-■= [Л "А "]+ [А"к"} ~.лГ\-\В"К' ] Ь . .+ (Я "Л "] ~3h> (82,8)

або

=[А"А"|

М"Л"]

H'VTj

[В"Л \ 1]г

ІЯ "Л ".(й -1 ))2

' {//"//".(/г — 1)] •

(82,9)

§ 83. ВРІВНОВАЖЕННЯ ВСТАВКИ ДВОХ ПУНКТІВ

У ДВА ТРИКУТНИКИ ТРИГРУПОВИМ МЕТОДОМ

(ЧИСЛОВИЙ ПРИКЛАД)

Розглянемо застосування тригрупового методу врівнова

жен-ня на числовому прикладі врівноваження тригонометрич

ної сітки (рис. 18). А, В, С, D — пункти існуючої тріангуля

ції; Е і F — нові пункти, найімовірніше положення яких не

обхідно визначити. Арабськими цифрами позначені виміря

ні кути. Вихідні дані див. у таблиці 64.

Таблиця 64

Назва кутів

Врівноважені кути

Н^зва сторін

Ig «

.11 + VI

64°02'28",16

АВ 4.267 8274

III + IX 37 52 27,35 ВС

4.312 5845

V + X 78 05 04,49

СА

4.325 1400

XIII + XVII 52 45 39,36

4.349 3125

XIV + XIX 65 17 19,68

4.146 8917

XVI + XX 61 57 00,96

Д ля визначення положення двох пунктів, крім 4 необ

хідних кутів, були виміряні ще 16 додаткових. Отже, в даній

сітці врівноважені кути повинні задовольняти такі 16 умов

них рівнянь:

І група

Умовні рівняння сум

1. ( 2) + ( 6 ) + wt

2. ( 3) + ( 9 )+ тг

3. ( 5) + (10) + да3

4. (13) + (17) + го,

5. (14) + (19) + ws

6. (16) + ('20)+ до6

7. ( 1) + ( 4) + ( 7) + ( 8 )+ д а , = 0

8. (11) + (12) + (15) + (18) + а / ,- 0 \

II група

9. ( 1) + ( 2) + ( 3) + да« - 0

10. ( 4) + ( 5) + ( 6) + о^ “ 0

11. (15) + (16) + (17) + z»T = 0

12. (18)+ (19)+ (20 )+ - 0

13. ( 7) + (10) + (11) + (П ) +

Умовні рівняння горизонтів

■ о

Умовні рівняння трикутників

14. Полюс в точці Е:

III група (полюсні умовні рівняння),

sin II sin V sin IX

15. Полюс в точці F :

sin III .'ІІ1 VI sin X “

sin XIII sin XVI чп XIX

■ 1.

16. Полюс в точці E.CFB:

ьіп XIV sin XVII 'in XX

sin VIII sin (Х + ХІІП Sin XIV

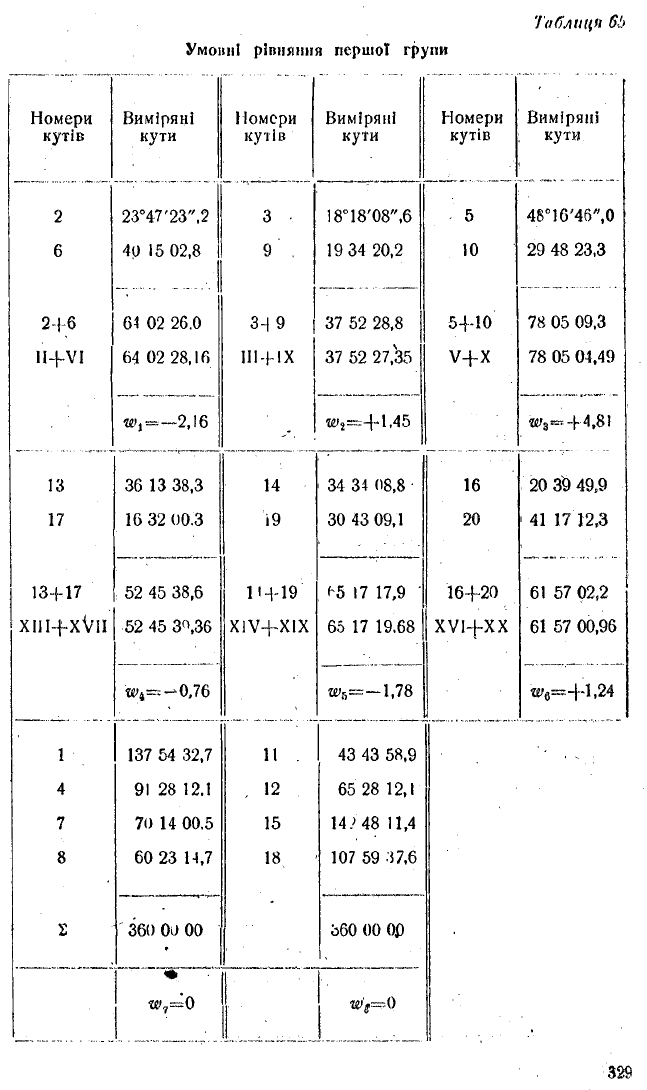
Номери

кутів

Виміряні

кути

Номери

кутів

Виміряні

кути

Номери

кутів

Виміряні

кути

23°47'23",2

3 18°18'08",6

48°16'46",0

6 40 15 02,8

9 .

19 34 20,2 1 0 29 48 23,3

2 + 6 64 02 26.0

34 9

37 52 28,8

5+ 10 78 05 09,3

II+ V I

6 4 0 2 28,16

ІІІ + ІХ 37 52 27,35

V + X

78 05 04,49

«>, = —2,16

k>s= + 1,45

«-’з- ‘ + 4,81

36 13 38,3 14 34 34 08,8 16 20 39 49,9

17 16 32 00.3 і 9 ЗО 43 09,1

2 0

41 17 J2.3

13+17

52 45 38,6 1 1 + 19

17 17,9 ■

16+20

61 57 02,2

хм i-f-xV ii 52 45 3f>,36

X1V+-XIX

65 17 19.68

Х У Ц -Х Х

61 57 00,96

да4=:-^0,76

wh— — 1,78 We~+-1,24

і 137 54 32,7

11 .

43 43 58,9

91 28 12.1

, 12

65 28 12,1

7 70 14 00.5 15 14/48 11,4

8 60 23 14,7

18.

107 59 37.6

36O0J00

360 0 0 Ор

♦

І.

w7= 0

j 0 ^ = 0

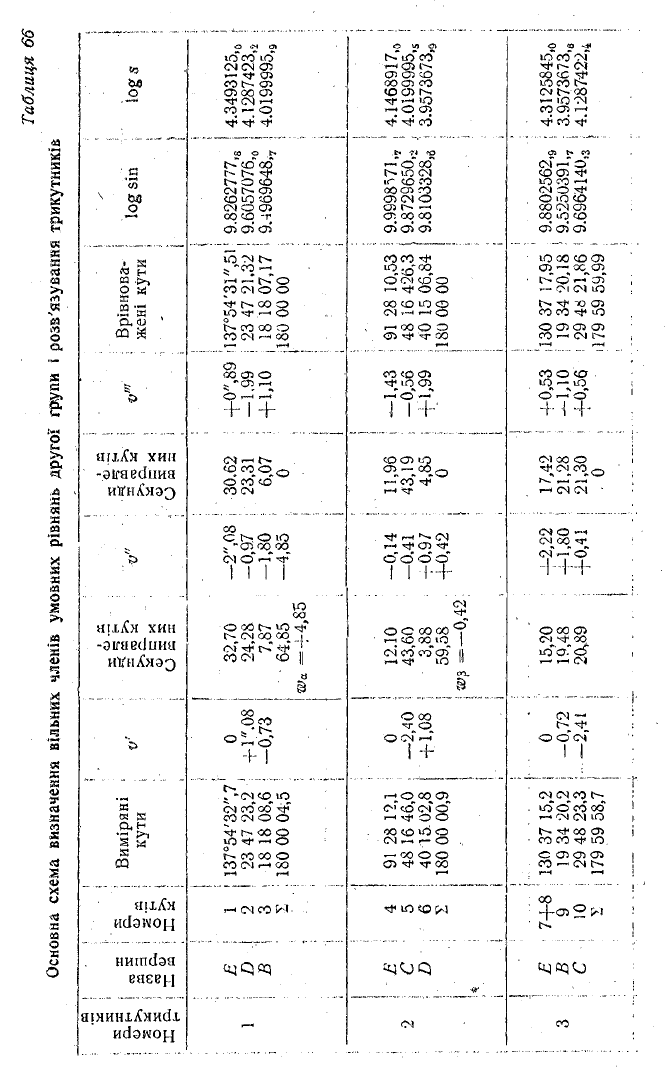
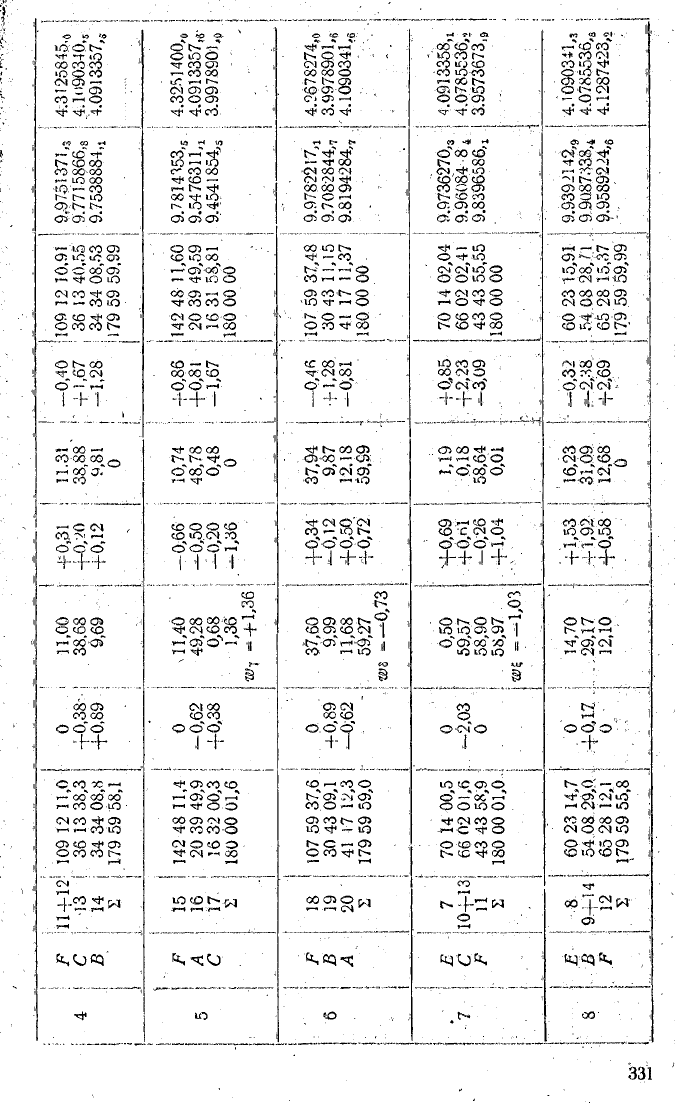
Основна схема визначення вільних членів умовних рівнянь другої групи і розв'язування трикутників

§-

«О

• 23

2 «

£ в

о . 4»

CQ й

оіхХх хин

-зігавсіїша

иїНіїлзо

а[іХл хин

-оігавсіаиа

итґн Хя з з

' £

« К

О , н

к*Ч

C Q

яіхХх

исізнон

нитсіза

ваєвн

aiMHHiXHHdx

ndawoH

ЮСО ю

СЧ CN Оі

— 05

to t-» СП

05 00 05

^ <М »-ч

со —_ о

r f r f

t"- СО со

N ь ^

с— о со

C N С " - О

<ою©

0 )0 0)

00 СО -г

05 05 05

Г-. ^ Ь, О

СО <М о о

^ tN C O O

LQ VT -—' О

Ь- со 00 О

СО СЧ -~ч 00

00 05 О

t "0 5 г-н

О г-н' г~1

+ 1 +

СЧ г-н Г -

<о со о 0

о со* <о"

СО CN

С 1> о ю

ч -05 оо 00

<Sl О* ~

• О 00 ^ ю ^

Г- (М СО 00 _1.

of ^ с-^ ,

СО <N со

оо

О со

*^•■5

+ 1

<М со оо Tf

СО CN о о

xfh«000

ю ^ г^ о

^ со 00 о

СО С4! г-н 00

« W C 0 W -

cyQcq

С-- ю со

r t O J O

05 05 сО

00 05 СО

«О 05 Г"-

т-4 о 05

rt5 со

— О со

С4- Ю СЧ

1C со со

00 СП СО

05 CS о

05 г-, -ч

05 оо 00

05 05 05

СО СО ^

“W 00.

О О» со О

•— ^ о о

СО со ю о

eq ,-н 0

гнсооо

СО со 05

r f Ю 05

г-Г о “ гг*

Г~* ^

Г-t r f 05 rt*

о О 00 СО

*-i со 00^ iO

сч со со о>

Г-н ^ ю

О ОО

’«Г О

о Ы г- “

і +

г-н о СО 05

С4*" со оТ сГ

H v f O O

оо со Ю о

СЧ — г - О

— СО О О

о ГГ 00

<tic<ow

sqCjQ

Ю со 'М

•Ф г - CS

С О с о ^

Ю со t"-

CN t - 00

— ю сч

СО 05 Т-*

со TjJ

(М г-н о

СО 05 rf

ю со —•

<N о

О Ю со

СО С4! 05

со Ю со

05 05 О»

Ю СО со 05

05 ~ 00^05

К о #~Г оГ

— OI 04 ю

N ^ X ) 0 5

со со ^ Ю

О 05 05 05

СО ’—1 сч с-*

со О со

Ю — lO

o 'г *

* о

« О н

(М 00 -^г

О с о о »

С 4 » 00 .

іооГсГ

г-н С4!

<N —

С"- T f

( N с ч с о t - «

Ю О с о 0 0

»-н <м <м ю

^ 00 05

С О с о ^ Ю

<С 05 05 05

со — <М С"-

-f-05<

S'.

cqcqcj

О 1Л '«

ю о" • 1

'ГГ ~r tQ ,

00 СО СО 1

Ю О СО

СЧ 05 —

— С 05

СО г-н О

О СО о.- '

О lO О

•чг СО 05 1 і

Г— СО 00

СЧ 05 05 ,

СО О 05

'ф ^ СО

О «О ‘О-

’ЧІІ *—1 т—« ■ .:

о ^ » <

СЧ 05 со

00 со О

r-~ ^ 05

с© 05 О .

С» 05 —J

^‘со^5 '

*•-*' со

Г- СО ОО

СО СО ОО

LO ОО

■IQ.'— СО

г- t-» ю

05.t> О.

05 05 05

ід >ч ю

СО ^

Ю ГГ Ю

с** СО 00

■<* со —

rnN -ф

00 ю

г-^ Ю ^

05 05 05'

С- t>

^ ■ф"

— гг оо

СЧ 00 СЧ і

. f>J O'*

00.00 05 " ,

Г- о 1-і 1

, O'- г- СО

03 05 о»

109 12 10.91

36 13 40,55

34 34 08,53

179 59 59,S9

О О )-1

СО Ю СО

т-* 05 СО* О

— чГ ю о

СО 05 ^ о !

Tf СО СО О

СЧ О со О • ■'

гг сч »-• со

107 59 37,48

30 43 11,15

і 41 17 11,37

; iso оо оо.

О N СО

чг СО СЧ

о —“ ~

. 1 + 1.

V ■ \

СО t4-*

со со со

о" о*1 »-?•

-1-+ 1 ' :

сс со' *-<

чг СЧ СО

О4—■'о

і + \

1 11.31

; 38,88'

I ^,81

! о

^ 00 00

t"> Г- о 1

о” СО о" ,

у -н rf

^ г-- СО 05

. 05 ос —; 05и .

t-“ 05 СЧ Ы

СО -4 10

- с м

СО, 7s’ *—<

о^сГо"

.)-

СО О О со '

«о ю.сч го

o' o' o' г-н"

! 1 ! 1

^ с ч о ’сч

со - iqts

о'сГосГ :|

+ :!+ +

О 00 05

С со СО

г-" ОС 05

і ' СО

со

О 00 СО сО .

CN со СО 4-

гн'сй'о'1^ ||

r-t ^ 11

со

О 05 00 1^ Р 1

С0^05^С0^СЧК 1

■i't—* "05 Г-н "'05 ІІ 1

СО г-, ю 11

СО .1

4-0,38--

; +0,89

СЧ оо

СО со

О o'o'

J +

05 CN '

со СО

о. o 'о* ,

-1-і

109 12 11,0

36 13 38,3

34 34 08,8

179 59 58,1

^ 05 со со

-г050*'^

Г-н О О

СО 05 СЧ о

•*=f со со о

СЧ о со О

rf СЧ г -- СО

СО >—< СО О

а> 05 1

CO .Ov— ю

05 СО (''■* 05

Ю -г- iO ,

h - О — 05

О со T f с^.

"см

+ 2 2 ”

2 S 2 S W

^йЗ-ч;

50 ;

с о « о с о

' ю с о г -

с о Ю С О

•СО Ю СО

V— ОС

O '* O ' to

О О 05

чг СО

О 00 СО

С*-. 00

. сч.^кю

• СО СО СО

со о 05

СС со

<у. 05 ОО

СГ. 05 05*

^ — ю

О^'Ю

СЧ СЧ ю о

о о ю о

О СО СО О

СО ^ 00

Ю е о 05

С О С Ч О

++■1

05 оо ^ —«

• гн «0 ‘О

^ o' со o'

О ) .<-4 С О ■'. f

с о С ( М О

с> о*©'»-?.

+ 4- J ~ к

O N .O h гг

ЮЮ05 0 ) I

■О 05 СО Л [1 ,

lO ю ю

с о

ооГо

Ю сС^ 05 О

o' —' сс »-?

о о ю о

rf СЧСОО

^ с *г о

О COCOO

t- сс Ф 00

t- H :

«— <о со

-* СО СЧ

с о ю

O'lON

С5 X 00

О о - СЧ

• о *-•

л *«# <о

сч" СО ^

СО

»-*• СО CSH

~ Ч t > 0 5 4

05 00 00

СО о ю

05 О } 05 ,

05 0 5 05 - ’

— ь* 05

05 со 05

СО оо 00 05

сч о сч ю.

О ■чр'-Ю 05

со Ю' со Г-’

ГЧ со 05

со ^.<о..

О СЧ О? -

J ||; +

СО 05 00

сч О СО 0

cd »-Г сч"

со /-н

,-f-■

O N O .

■* ? 0 > СЧ

Г-С^Г-1

О О О

^Ґ СГз CN Ю

г-< С4 — ю

СО 00 00 05

сч о <м ю

О ^ Ю 05

со ЮСО I4-

СО _J_£J W

щсдй.

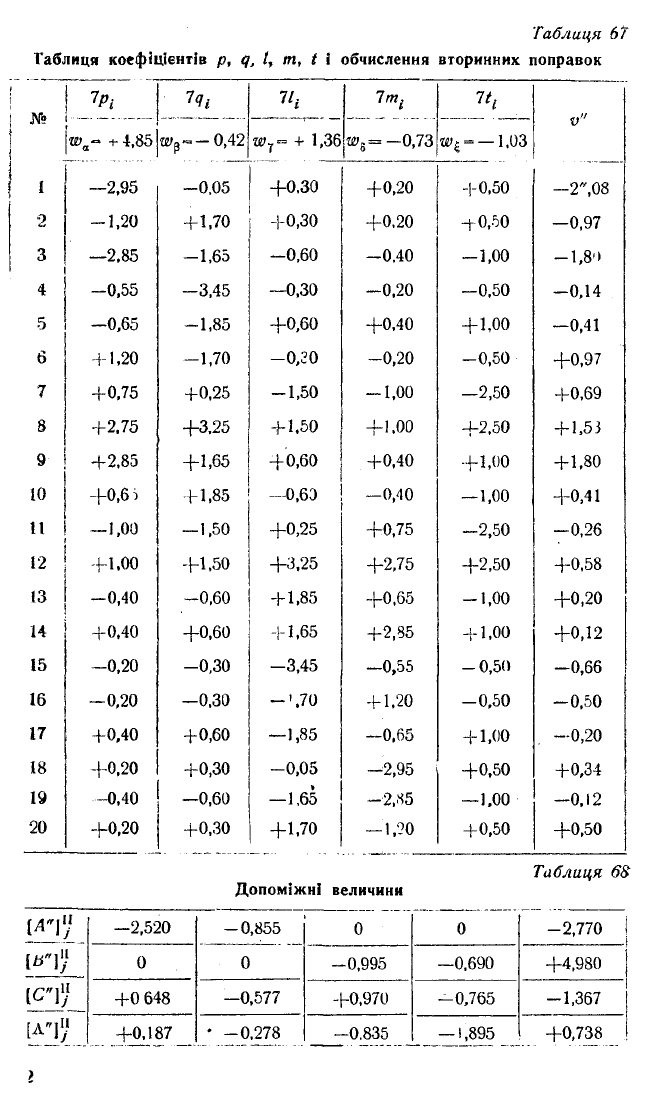
1 р і

7 ? і

7 т .

7'*

№

+4,85

0,42

ге>т= + 1,36 ® 5= —0,73

W f — 1,03

V "

— 2,95 -0 ,0 5

+ 0 ,30

+ 0,20 4-0,50

—2",08

-1 ,2 0 + 1,7 0

+ 0,3 0

+ 0 ,2 0

-г 0,50

— 0,97

— 2,85

— 1,65

-0 ,6 0

-0 ,4 0

-1 ,0 0

-1 ,8 '»

-0 ,5 5

— 3,45

— 0,30 - 0 ,2 0 -0 ,5 0

—0,14

—0,65 - 1 ,8 5

+ 0 ,6 0 + 0,4 0 + 1 ,0 0

— 0,41

+ 1,20

-1 ,7 0 - о , г о

-0 ,2 0

-0 ,5 0

+ 0 ,9 7

+ 0,75 + 0,25

-1 ,5 0 -1 ,0 0

-2 ,5 0

+ 0,6 9

+ 2.75 + 3 ,2 5

+ 1.50 + 1 .0 0

+ 2,50

+ 1,53

+ 2,85

+ 1,6 5

+ 0,60 + 0 ,4 0

+ 1 ,0 0 + 1,8 0

+ 0,61

+ 1,85

—0,63 — 0.40

— 1,00

+ 0,41

11 — 1,00

— 1,50 + 0 ,2 5 + 0 ,7 5

-2 ,5 0 - 0 ,2 6

4-1.00 + 1 ,5 0 + 3 ,25

+ 2,7 5 + 2 ,5 0

+ 0 ,5 8

ІЗ

-0 ,4 0 -0 ,6 0

+ 1,85

+ 0 ,6 5

- 1 ,0 0 + 0,20

4-0.40 + 0 ,60

4-1,65

+ 2,85 4 -1 .0 0

+ 0 ,1 2

-0 ,2 0 -0 ,3 0

-3 ,4 5

-0 ,5 5

-0 ,5 0

-0 ,6 6

-0 ,2 0

-0 ,3 0

— ',70

+ 1,20

-0 ,5 0

+ 0,40

+ 0,60

— 1,85

—0,65

+ 1,00

— 0,20

+ 0 ,2 0

+ 0,30

-0 ,0 5

-2 ,9 5 + 0 ,5 0 + 0,3 4

-0 ,4 0

—0,60

— 1,65

-2 ,8 5 — 1,00 -0 ,1 2

+ 0 ,2 0

+ 0,30

+ 1,7 0

— 1,20 + 0,5 0 + 0 ,50

Т а б л и ц я 6 8

Допоміжні величини

т "

—2,520

-0 ,8 5 5

0 -2 ,7 7 0

-0 ,9 9 5

—0,690 +4,980

іс" і1;

+ 0 648

-0 ,5 7 7

+ 0,9 70 -0 ,7 6 5 -1 ,3 6 7

[л -іу

+ 0,187

І і

> о

і ^

-0 .8 3 5 — 1,895

+ 0,7 38