Бугай П.Т. Теорія помилок і спосіб найменших квадратів
Подождите немного. Документ загружается.


kl—fllWa -{-••■-{-fit 1V~. - (80,10)
Так само, вводячи неозначені множники
f ’i< /22» •••> fit,
/зі> / з 2> •••! / з б
ftl, ft'i, •••, ftt,
(80,11)
знайдемо вирази для решти корелат у функції вільних чле
нів:
+ / 2гЩ + • ■ • + / * »
k*=fziw* +/з2^Р + - + / з < ^ ,
................................................................. (80,12)
kt= fnWa /дИ/р + - " + / « ВД' •
Очевидно, щ о неозначені мможники (80,11) можна ви
значити з таки х систем рівнянь:
[а'а '] / г і-Н 3-Р ] А’гЧ----'!- [а 'с/] J^2^—1—0 = 0 ,
[а 'Р ']/ 2і+ [? Р І/22+-••+[?
[* ^ '1 Л .+ ЇР ,х,]/ ї2+ ...+ [х Ч ']/ „ + 0 = 0 ;
(80,13)
[а'»'] /л -f-[a'P'] f п-\-■ ■ \ ftt-\-0 — 0 .
[ « т ] / « + [ т / « + . " + [ Р '- = '] / « + о = о , -
.................................................................................... (80,14)
[а ^ ']/ « + [Р 'х ']/ й -Ь - + [ ',- , ]/ „+ 1 = 0 .
Для обчислення других поправок vt" служить така загаль
на формула:
v і”= а і ' -j- р і'к2 “(“ ••• Ч~' і t • (80,15)
Підставимо в неї замість корелат їх вирази (80,10) і
(80,12):
v"i — а’і (fn wa-\-fl2w9 -\-...-\-fitW- )-j-
(/21 Wa "Ь/гг w? ~ К ••“b/s/Wt )4~
(ftiWa. -\-ft2'Wp -\-...-\-fttW~ ),

або, розкриваючи дужки і підсумовуючи по стовпчиках, -
<о і"ї— (а і 7іг!~Р і '/2і 4~-"4~х і Vfl )Щ 4~
+ («і 7 п + Р i'fu '/«) +
. , .
.
...........................'..............................................
..
(80,16)
і- (а і 'fu
.
Р < '/м +.■ z+'c і '/«) W* -
Введемо позначення:
Рі — а і 7 п “Н* ‘ 7гі4"'--4'х і 'ft\.
Я1 = « ,'/ , 2- f р і '/22-|-.. .- fx і '/ „ ,
/і = « / 7 18+ Р і ,/23+ - + ^ 7 « , (80,17)
ti == а і 'fit + F і 7 г # + . • г 'fu \
тоді
V'i — pi w « + q t + /,• - f ... 4 - 2і, Дот. (80,18)
Тут вільні члени ач/їі1',. необхідно обчисляти за ре
зультатами вимірів, виправленими первинними поправка
ми v'i, " •
Візьмемо тепер до уваги, що коефіцієнти при поправках
в умовних рівл-іяішях другої групи дорівнюють j-І і не зале
жать від величини кутів (цього не можна сказати про кое
фіцієнти полюсного умовного рівняння). Якщо в даній типо
вій фігурі тригонометричної сітки, (наприклад при вставці
пункта в трикутник або чотирикутник, нумерацію кутів і
розподіл умовних рівнянь на перші дві групи будемо завжди
проводити однаково, то для кожної типової фігури пере
творені коефіцієнти ОС/', IV,...,х/ умовних рівнянь другої групи,
множники fjk(},k~\, 2,..., t), а значить і рь Яі, U,
іі будуть величинами сталими. Тому їх можна обчислити раз
назавжди і для найбільш вживаних типових фігур скласти
таблиці1. Тоді другі поправки v" обчислюються досить про
сто за формулою (80,18).
Для обчислення третіх поправок v'" необхідно спочатку
зробити друге перетворення коефіцієнтів умовних рівнянь тре
тьої групи за такими формулами:
А А і'+ А А /,
В і "™ В і'+ АВ і\ (80,19)
Я/"- Ні' + Л Я ,',
і Такі таблиці надруковані, наприклад, у згаданій вище роботі
проф. О. І. Кобиліна.

де введено такі позначення:
Д А і ' = а і 'рп Р і 'р12 + ••• + ~ і 'Pit,
AS і'= а і ' р2і + Р і 7 Р22 + ^ г /Р2<,
.............
.....................................................
(80,20)
ДЯ і /= а і "pftl + P г ’Pft2 + ... + х < ' Pht*
Як відомо із загальної теорії двогрупового методу врів
новаження, допоміжні корелати р визначаються з таких си-
стем рівнянь:
К а']ри + [я т ]р і2+ --- + К х']рі t + [а'А’] =0,
[а'Р'1 Ри + [Р’Р ]рі2 + •••+[P’x ]pU“H P ,A ] = 0j
......................................................................
...............
(80,21)
[аЧ ’] ри + [р'т ] р12 + ••• + [х х ] Ри + [х'А'] — 0;
[а'а']р21 + [я'Р']р22-і ...+ [ a V ]p 2/ + [я'у5 '] =0,
[а>?/] Р21 + [р,р,]р22 + ... + [Р'т:']р2/ + [Р '5 '] = 0 ,
.................................................................................. (80,22)
[а'Х']?21+[Р'Х']р22 + -•• + [Х'Х1 Р2* + [х'£ '] = 0;
[а'а']рлі + [а'Р']рй2+... + [а'т,]рЛ;+ [а'Я '] = 0,
[а Р ] рлі + [р р ]рЛ2 + ... + [Р 'c’jpft/+ [р Н ] = 0,
.................................................................................. (80,23)
[а'х']р*і + [Р'т:']р Й2 + ...+ [-cV]pw + [V//'] = 0.
Порівнюючи ці рівіняння з нормальними рівняннями ко
релат (80,7) другої групи, бачимо, що вони відрізняються
від них лише назвою 'невідомих та вільними членами. Отже,
ми можемо допоміжні корелати р визначити в функції віль
них членів рівнянь (80,21), (80,22), (80,23) за допомогою
тих же неозначених множників /, за допомогою яких були
визначені і корелати k\, k2, .... kt- Д ля цього досить у рів
няння (80,10) і (80,12) замість ге/,,, щур, .. , W- підставити вільні
члени рівнянь (80,21), (80,22), . . ., (80,23):
Р і г = / и М ' '] + Ш Л ''] + • •• + fu [ x 'A '],
P i^ fiiW ^ -'] +/2 + fot{i’A'],
........................................................................... (80,24)
p\t—ft\ [а,Л '] + / /2[р А'] + ... -Yftt\y А ];

PS1- /ll [ “'S ']+/l2[P 'fi'] + .-.+ /,/ [X'fi'j,
P22 =fzi[a'B ] -Ь/ггІР ^ ] + .--+/г<[х В’},
........................................................................ (80,25)
p2, - u [*’Bf] + /«[Р 'Я '] + ... + / « [*'£'];
Р й і= 7 п К Я '] + / 12ІР 'Я ’] 4-... +fu Ь ’Н ’],
9н*‘ М *'Н']+ЫРН’] + - + и b'H'l
.................................................................................. (80,26)
Р н1= М « ,Н ’Ш <2ЇЇ'Н ’] + ...+ М і'Н '} .
Легко довести справедливість таких співвідношень:
[а'А') - [а Л '] = [A'Yl, [х'В']=[аЕГ] = [5 ']«,
[Р'Л'] = [рл'і = и ']',1, [ т = \ т - ] в ' ] і
Ь'А'] = [хЛ '] = [Л ']», [х'Я'] = [хЯ ']~
............................................................................................... (80,27)
[а 'Я ']- [ * / / '] - [Я ']1,1,
[P'tf'] - [РЯ'] = [Я ']«
[х'Я '] = [хЯ '] = [Я ']
де [Л ']J?, [В')1)
...........
[Я ']1] (/= 1, 2, ... , І) — суми коефіцієн
тів при тих невідомих, які входять в у'-е умовне рівняння
другої групи.
Доведемо, наприклад, першу групу формул (80,27). За
гальні формули для обчислення перетворених коефіцієнтів
умовних рівнянь другої групи такі:
а,’і = щ -J- а{ р 'и -f- bi р'12 гі Р V ,
§'і = Рг + о.і р'2і -\-Ьі р'22 -j-...-f- ri pV>
Xа/ = X,- -j- d l р ’п -f* Ьі р’t2~\~ •••"'Ь ri Р 'try
te p ’jk (/ = 1, 2, . . . , t; k = 1 ,2 ,..., л) — допоміжні корелати.
Іомножимо кожне з цих рівнянь (при різних значеннях ін-

декса і — 1, 2, . .. , п) на відповідні А\ і добутки підсумуємо.
Одержимо такі сумарні рівняння:
[а'Л '] = [яЛ '| + [Л '],р п ' + [А'ІзРіо’ + • ••+ [Л J»-
[Р'Л'] = [ M l + И 'ІіР гі' + H ' W + -.+ [А']г р8/ ,
...................................................................................................... (80,28)
[х'Л'] => [^Л'] -f [Л ']хр;і'+ [A^zPti' + ••• + [Л ']r Ptr,
де [A'\k {k— \, 2, ..., r) — суми перетворених коефіцієнтів
А' по секціях, які утворюються умовними рівняннями пер
шої групи. Ц і суми дорівнюють нулю. Крім того, слід пам’я
тати, що а.і = фі-=... = х/= !. Отже, рівняння (80,28) наберуть
такого остаточного вигляду:
К А ' Ь И ' Н 1,
[Р 'Л 'М Л ']»
К Л ']= [Л Т / .
Так само можна довести вірність і решти груп рівнянь
(80,27). Тоді формули (80,24), (80,25) і (80,26) для обчислен
ня допоміжних корелат, необхідних для другого перетворення
коефіцієнтів Л і\ В Я ,'ум о в н и х рівнянь третьої групи,
можна записати так:
Р п = / и [ Л У + / і2 И Т ^ -..-+ / і^ т / ,
рп-М АТ' + АЛАТ.Ї+.-.+АЛа'}",
■ + М л ? } ,
р21 = / п [ П І + / 12[£ Т 2, + ..
■ + M B W
P22=/2i m i , + /22[S']” + .
••+ Ы В ’)",
Р« - / « т ч + м в ' ] 1!- ь . .
+ М В '] 1},
р « - / и т \ 1+ м н '] " + .,
■ • + / «[« Т/,
р и = / 21[Я Т 1, + / 22[ Я Т ' + .
~+МН')Ч
Phi - / я [Я ']1/ + М Н ']" + ..
■ + / « №
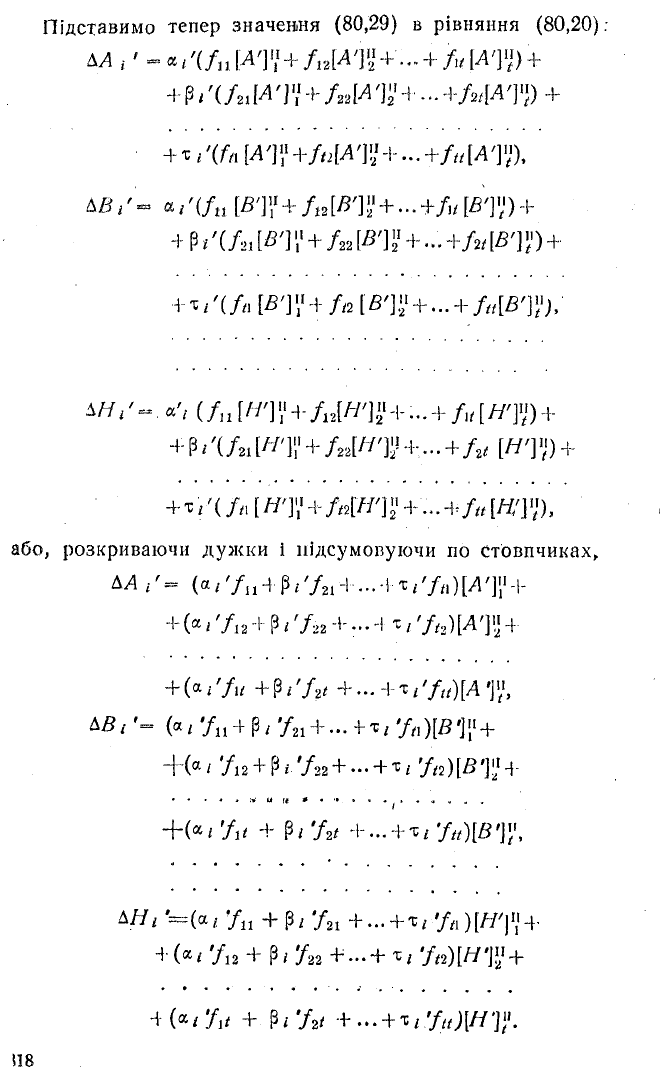
Підставимо тепер значення (80,29) в рівняння (80,20):
Д Л ,-' = * V ( / n H 1 ^ l/ r ,H T J + --- + /u И ']») +
+ Р / '(MA'Yl + /22 И 'Ji'+... +/*HTJ) +
+ *, ЧЛі ИТ/ + /« и /]ї + ...+ /« И IV),
Л Я , '- *./(/и [5Т,г + / 12[Л,]" + ...+ / к Й ' і) +
-і- р і ■4/21 m і1 ■+ /22 т а+... +/« їв'} ’>)+
+ х / '( / « [В']» + U [S 'Ji1+ ... + M B '} 1'),
Л Я ,' ~ (/„ т и 4- / 12[ Я '] « -І-... + /■„[//']») +
+ р і '(/21 т і + м и 'ї} +,..+/** [Я']1;)+
+ х і'( / я [ Я '] '1І + /«[///] 'Ч . . . + / « [ « '] у ) ,
або, розкриваючи дуж ки і підсумовуючи по стовпчиках,
М , ' - (а , У п 4 р, '/ 21 -І ... -І х , 'fn)[A'}" -I-
+ (* « У іа + р ,7 и + г.н ^/7<2)HTJ +
+ (а І 'fu + р , 7 ?/ + ... + х , 7 „)[Л 1»,
Д£ , '= (а , */,, 4 Р , у 21 + ... 4 х , уп )[В'] и +
+ (« / '/і2 + Р<- У22 + ... + ^ 'fn)[B']"4~
...................
...
U «*••»... f , , „ v „ .
+ (* / 7l< + Р* '/2/ + ... + Х, /« ) [£ '] J',
ля, •=(«/ 7п + р/ 'Лі + ...+Т / 7д НЯ'^Ч-
+ («і 7і2 + Р / У22 +... + X, 7«)[Я']»4-
-Н«/Уі* + Рі 7г< +... + х ,7 «ля^'.

Якщ о тепер взяти до уваги позначення (8 0 ,17), ф орм у
ли для д ругого перетворення коефіцієнтів ум овних рівнянь
третьої групи остаточно виглядатим уть так:
А, А , '+ рі [Л ']” + Чі И ']£ + // [A1}" +... + ti [ Л 'j” ,
Д Л - В, '+ pi {В'}" + qі [ВУІ + lt \В'Щ Л-... + ti [B’Yl
................................................................................................. "
.............................................................................(80,30)
Н ґ - Ні •+ pi [Н']■'!+ ь [Н']"+іі [H'\"+..,vti [нГг
О тж е , ми бачимо, що друге перетворення коефіцієнтів умов
НИХ рІВ'НЯНЬ третьої групи проводиться досить легко за д оп о
могою тих же величин pi, qit U, і і, за допомогою яких
проводилось обчислення вторинних поправок і'і" за ф орм у
лою (80 ,15).
Д ал і складають нормальні рівняння корелат, щ о відпо
відають умовним ,рівнянням третьої двічі перетвореної групи:
\A”A"}K,MAf'B”\K2 + - + [A”H"}Kh + W,- 0,
\A"B"]Ki + [B"B"}K2 + ... + [B”H"]Kh + W2 = 0, (80,31)
[,A"H"]K1 + \B,,H"\K2 + ... + [H"H"]Kfl + Wh = 0.
Т ут вільні члени обчислюються за результатами вимірів,
виправленими первинними і вторинними поправками.
Роз в’язуючи рівняння (8 0,3 1), знаходять корелати К, тре
ті поправки
ю Г - А і ”К, + В і" К2 + ...+Н і "Кн (80,32)
і, нареш ті, остаточні поправки
Vi - V i' + v / ' + V i" ’.
§ 81. ВИЗНАЧЕННЯ ВАГИ ФУНКЦІЇ
ВРІВНОВАЖЕНИХ ВЕЛИЧИН ПРИ ТРИГРУПОВОМУ МЕТОДІ
ВРІВНОВАЖЕННЯ
Нехай маємо ф ункцію врівноваж ених величин
/(I, II,..., ДО. (81,1)
Д ля приведення її до лінійного виду замінимо врівнова
жені аргум енти через виміряні їх значення плюс 'найімовір
ніші поправки до них:
1=1+®!,
І Ї-2 + u,,
N ~n + vn-,

будемо мати
/ (I, II,..., N )=f(\+vlt 2 iv 2,..., n + v„).
Розклавши цю функцію в рядок Тейлора по поправках vir
одержимо:
/(I, II,..., А 0 = /(1 , 2,..., п) +
(81'21
Але при тригруповому методі врівноваження
Vi = Vi'+ Vi"+ Vi'";
отже, позначаючи часткові похідні функції
( | ) 0- Л « , (81,3)
функцію (81,2) можна записати остаточно так:
/(I, II,..., Л 0 = /(1 , 2,..., Я )-І-л, « + < + < " ) +
A2(v2' + v2" + v2"') + ■ (81,4)
л„ (vn ' -Т Vn"+ Vn"').
При груповому врівноваженні методом трьох груп поправ
ки Vi', v", vl" виражаються через корелати так:
v і ’ = а ,- kx 4- bi k2 + ... 4- г-, kr,
vi"= *i’n'1+Pi'k2' + ... + xl'kt', (81,5)
Vi"' - Л і" К, 4- В і"К2 4-... + Н і "Кн .
Підставивши ці значення поправок в (81,4), будемо мати:
/ (I, II,..., Л 0 = /(1 , 2,..., л) +
4- Aj(fljfej + b\k2^r... 4- v^kr -\-fi^ k2 + ... 4~
+ zl’k t'+ A"Kx+B ”K2 +..• + ИКн) +
-\-K2(a2kl + b2k2 + ... + r2kr+a2 4- fi2 k2 + ... +
+ z2'kt' + А2"Кх 4-B"K24-... 4-H2Kh) + (81,6)
4-Л„ (an k i 4- bn k 2 4-... 4- rn k r 4-an 4- fin 'k 2 4-... +
+ *n'kt'+ An"Ki + Bn"K2 +... + HnnKh )■

Після розкриття дужок .та приведення подібних членів по
корелатах функція (81,6) набере такого вигляду:
/(1, II,..., N) =/(1, 2,..., п) +
-f [rtA] /?! 4 [М ] k 2+ ... + [гЛ] к г-і-
+ [а'Л ]Л ', + [Р'Л] *'2 + ...+ [т'А] k't + (81,7)
+ [А"А] Кх + [В" А] К2 + .. + [Н"А] Кн.
Для визначення оберненої величини ваги функції (81,7)
необхідно залежні між собою корелати виразити через без
посередньо виміряні величини. Д ля ЦЬОГО ПОМНОЖИМО нор
мальні рівняння, що відповідають першій, другій перетворе
ній і третій двічі перетвореній групам умовних рівнянь, на
відповідні неозначені поки що множники:
*11- 1Г12--"; г,
тс21- 1с22і,,ч (81,8)
*31- ^Я2> "> тс3й>
де перші індекси означають групи, а другі — номер нормаль
ного рівняння в групі, і одержані добутки додамо до ф унк
ції (81,7):
/( I, II,..., Л 0 =/(1, 2,..., п) +
-і- [аЛ] kl + [М ] k2 +... + [гЛ] kr + [я'Л] k\ + [Р'Л] k’2 ... +
\-[z'A]k't + [А"Л] К1+[В"А]К2 + ...+ [Н"А]Кн +
4-{[аа] kt + [ab] k2 + ...+ [ar] kr -f ®;1} п 11 +
4 {[ab] kx + [bb] k.2 + ... 4- [br] kr + ®2} 1ci3 +
-V{[ar] kt-\- [br] *2 + ...+ [rr] kr + wr}r4r +
+ {[а'а'] ki + [a’P'] [^ V ] k( ' + Wa } *21+
+ {[* '£ '] V + [P T ] k 2 + — + [P'X'] kt ’ + Щ }*22 +
...................................................................................................(81,9)
+ [ї'15'j ki + [(3 x’] k2 + ... + [x'z ] k'( + Wz } TC2< +
+ { [A"A"] Ki + [A"B”] K2 + ...+ [АЧГ] Kh +
+ {[A"£"] Кі+[Ь"В"] К2 + ..Л\В"Н"]Кк + W2}* S2 +
+ {[AaH№] Ki+ [B"H"]K2 + ...+ [H"H*] Kh + Wh)^h,

Розкривши дужки, після зведення подібних членів по ко
релятах будемо мати:
/(I, II
......
Л0-/(1, 2,..., п) +
-\-{\аа\ кп-\-[аЬ\ « і2 + ...-(- [а г ]іс і,+ [ а А ]}Л і+
+ { [ аЬ\кп-\-[ЬЬ] -.+[&/■] кіг-\-[Ьк}}k2-\
’ К М « 12+ - + М « і г + [ г А ] } Л , -f
+ {[* '* '] ~2i+ laT ] " 2 2 + ~ + [a V ] K2rf [а 'Л и ^ 'Ч -
+ { [ « Т ] * 2 гИ Р Т 1 ^ г Ь - Ч Г * ' ] *2, ІЧ Г Л ]} V +
.................
: .............................................................................. (81,10)
+ { [* V ] Я21-}-[р Ч '] *22+— Ч -Г "4 '] Я 2 < + К Л ]}Л ^ +
+ { И " Л " ] *31+ [Л "3 "] *32+ ...+ [ Л " / Л « з л + И ' А ] } ^
+ {[Л "5 "] *31+ [S "£ "1 u82-f ,..+ [ f l ^ ] ЛзН -[^ А ]}А Г 2+
^ зі+ [^ "Я "] *82+ . . + [ / W ] хзл+ [Я"А]}/С*-1
-|-И)і*и+да3т:12+ . .. + ^ '
- [-даа *21+Wp т:22 + ” -+® ,т *2;+
+ U7i*31+ \ r 2x32 -K ..-!-^ t *3ft.
Користуючись неозначеністю М'НОЖНИКІВ підберемо їх
так, щоб вирази у фігурних дуж ках дорівнювали нулю. Тоді
дана функція буде виражена через вільні члени умовних рів
нянь, які безпосередньо зв’язані з результатами вимірів, і
неозначені Міножники
/ (I, I I , iV)=/(l, 2 ,..., л ) +
~\~Wl'!Zll~>rW2'IZl2+ ” -+®V “ І'+
4-®V * 2 + даэ - 22+...+та/т *2rf- (81,11)
г ^1*31+^2*33+- +
Тепер до функції (81,11) можна застосувати загальну фор
мулу . для визначення оберненої величини ваги функції не
залежних між собою рівноточних величин:
Р/ ^\д і)
Знаходимо часткові похідні функції (81,11):
jl = А/ + йі Кп-\-Ьі " 12+ - ” ‘| г < '"іН -
+ а , /п:21+ р , 'r 22-j-...-f-x і '*2<+ (81,12)
j - л "«31+В , "*32+ . . , 'ГН2 ”щн.
