Бугай П.Т. Теорія помилок і спосіб найменших квадратів

4. Умовне рівняння трикутника BCD

Q) _ + (? Ж 5 )± (6) +_ 2",80 == 0.

5. Умовне рівняння горизонту

(3) ! (8) ! (11)+(14) 4- (17) 4-(20)—О",92=0.

6. Визначення коефіцієнті® вагової функції

Для оцінки точності результатів врівноваження визначимо

середню квадратичну помилку т,g AF в логарифмі сторони AF,

найбільш віддаленої від вихідної сторони CD, Отже, вагова

'функція матиме такий вигляд:

/ = l g AF — Ig CD

sin V slnjx sin XII sin XVII

sin VIII sin X sin XIII sinX V i'

Таблиця 60

/ = / 0+ 1,58 (5) -2,37 (8) 4-0,69(9) -1,17 (10)+

+ 3,67(12) - 1,55 (13) —3,25 (16)+0,54 (17),

де

/о = = lg CD

sin 5 sin 9 sin ’2 «in 17

sin 8 sin lOsin ІЗ sin 16

Чисел ьни к

1

Знамен ни к

Ном'ери

Номери

кутів Кути

А

кутів Кути

Д

«

5

53°04'28",5 15,8

8

4Г41'26",0 23,7

9

71 43 42,6

6,9

10

60 47 34,2

11,7

12

29 50 44,2

36,7 13

53 42 07,4

15,5

17

75 37 44,9

5,4

16

32 54 18,9 32,5

Примітка. Коефіцієнти і вільні члени полюсних умовних рівнянь і

пшопої функції зменшені в 10 разів. Вільні члени умовних рівнянь дру

гої групи обчислені за кутами, виправленими первинними поправками.

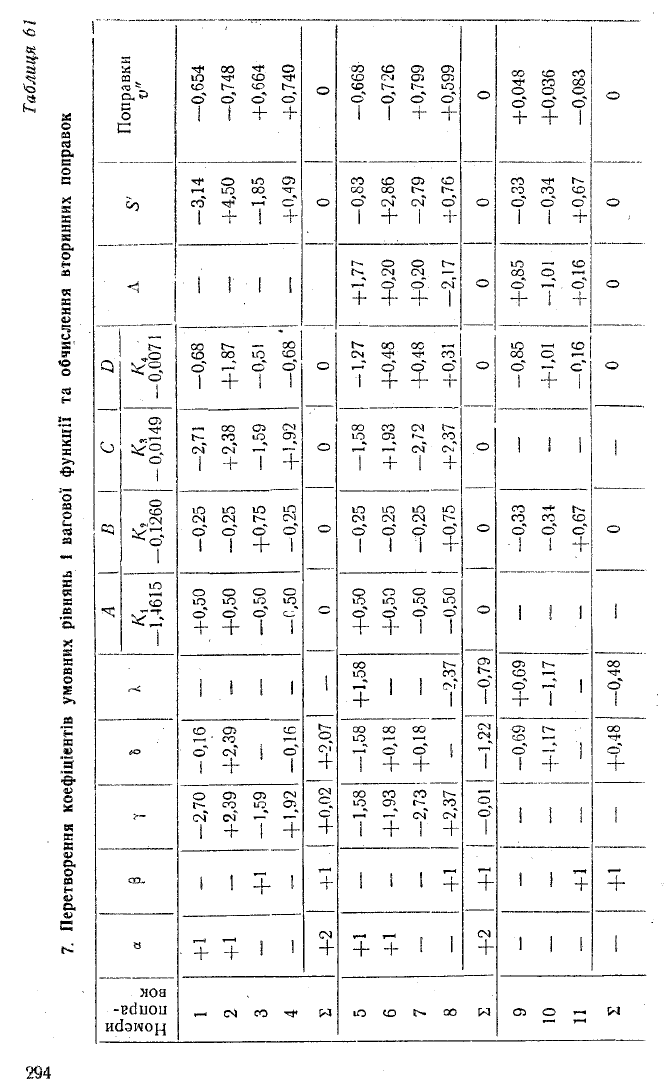
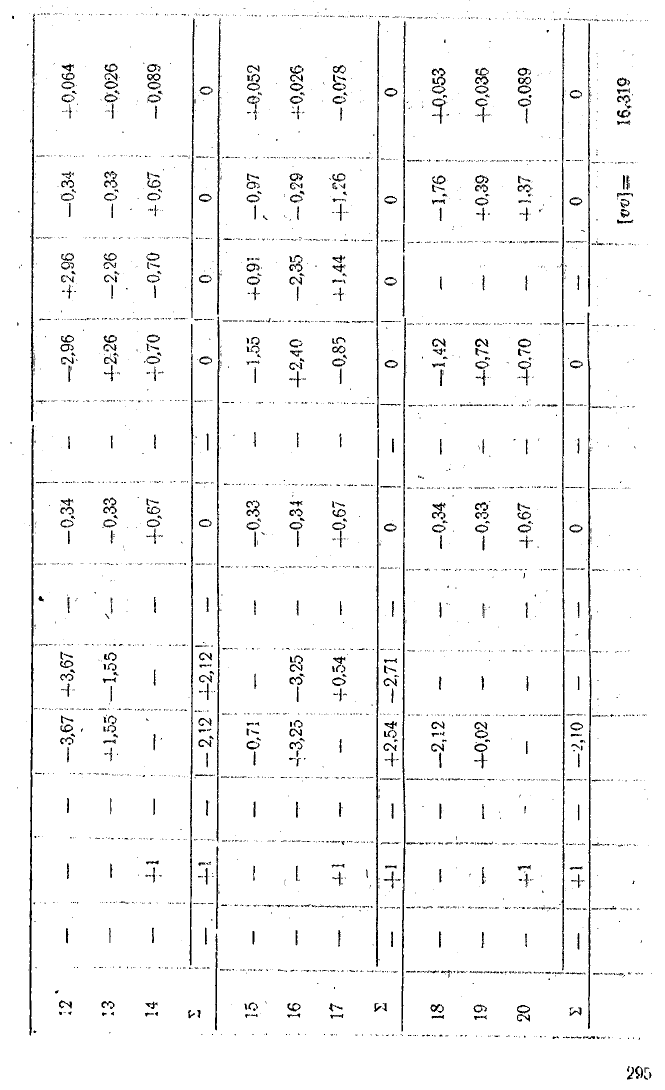
Перетворення коефіцієнтів умовних рівнянь І вагової функції та обчислення вторинних поправок

с а ,

*4

Си

С

О

а

со

CQ

-«.о

* §

о

QD

ю

CD

лоа

-Eduou

иёэиоц

n

o ’

тГ> о

CO

С О Г - .

о о

+ +

с о

1

1 +

со

CD

с ?

ОО Ю CD

О о "

I +

CN СЧ

1 +

05 О»

Ю С\

1 +

ю ю ю ю

М (N N <м

с ? о o ' с Г

1 1 + 1

о о о о

Ю Ю L Q ю

о' о“ о" cS

+ + I I

о CN

I +

с о

СЧ

і +

! +

+ + і

ОО <D О O i

CD (М O J 0 3

со г- N ю

о “ о" o ' o '

I I -г +

О CN сч

I + I

О О N

С М О ! —

o ' o '

+ + + I

о

ю ю ю «о

CJ сч <м о-

о с> о ' р "

1 1 1 +

g

o о о

ю ю ю

o ' o ' о 4 о “

+ + ! I

+

ОО С О с о

lO 1—1

o ' о ‘

! + +

оо с о С О

ю о> г-

1- ? — " C N

I + 1 +

*1~

+ Н"

+

(М

+

0 0 с о с о

^ с о с о

О О О

о о о

СО

С О с о

с ? о "

1 I +

со о

о г-Г .

+ 1

СО

О г-

о —

і +

ГО -*+• N

со с о с о

с ? 0 “ о “

+

о

о ”

о —

I +

і 1 +

о

+

CD

О

4 :

<c> a?

СЧ oo

о о

• o'

-1 1

о

(X

]Q

о

qT

<£*

CN

о

;|.

00

c>

f

О

СО

ю

о

■'; ?

CD

CO

о

a‘

"1

a*.

oo

о

і

O

-

.....

.........

.

— .

__

...

....

•

-0,34

CO I'-

СО о

о o'

1 ■ -1-

о

a>

о

1,

o>

CM

G>

.1

Ф

(.'i

qi

о

tD

7

O)

со

о

4-

t'-

CO;

4 ’

O

-----

--

.....

.........

.....

-- -

...

—

.

..

.

......

ю

о

CN

-f

о о

СМ 1-.

о-Г o'

! ■ 1

о

ov

о

-f

. vO

CO

CN

1

rt*

1 ^

4

о

і

1 і

1

— -

.

...

.......

:

....

—

-------

J

-----

—

.

......

..

_

__

ї£>

o>

І CN-

. ,,

<о о

cn , ь-

cn .о“

4" 4“

■о

Ю

IO

.. -J

О

ТЗ*

CN

4-

tr>

00

О

1

о

CN

7

CN

t-

O

4

о

і--

' $

o

I

1 !

• I

■ 1

I I

1

i

'1.

■ t

1

. rf-

CO

О

1

СО 1--

со <£>

о о 4

1, 4~ -

о

8

o '

г

CO

o“

1

<£> .

C>

+

о

CO

о

1

CO

о

1

fe

o'

4™.

о

‘ !

■ j і

!

і

1

!

1

Г l ’

1

&

CO

H"

. ю

3 1

I

CN

-1

1

IO

CN

CO1

1

»o

О

-1"

CN

1

-3,6 7!

IO

iO

і 1

CN

1

l'-

o

1

lO

CN

co1

1

~r

!

ю

CN

+

CN

1

CN

О

-f

1

о

1

— .

,

-----

__

____

___

_

__

1

I 1

1

і

!

1 1 ! .

I

1

.

1

1 H-

’ 1 ; I

+ '

1

'

rx

+ ;

+

| 1 1

1

1 I I I [ 1 | І

1 1

1

I 1

1

I

1

CN

СО 4*

*“i W

Ю '

2

v—»

CO

s

O

CN

16,319

0?

ar

a

*2

Co

О

о о

о ю

СП Оз

1—_ о

СО СО

+ I'

со о со о

h-

Ю

■""ч

со

ОО

ОЗ

00

Г"-

03

О

со

f-

со

ю

Г-Н

о ю

N оо

СП о

о

+ I

$

і

о о

о - о

о , о

сч

+1

! I

+ + + I

о

О

со ю

СО

со

оо

t'-

<N

Оз

ся

о

.—Г

О*

о

о ”

+ I +

о о о о о

(М О со со со

ггз ^ — —

о —* о о о "

I + + I I

О О 4 t

О О —

О О О

см о

о о " о '

+ і +

О О О

СЧ — О

О О О

О ' о о

+ I +

О О О

О О

О О со

о ю о

y- ї о о

I + !

о

оГ

+

ВННЭЬЕНеОи

N о

03 О

0 3 О _

•— 1 CN СО

о с ?

0 3 ОО

0 3 о

- + + + S

со

С'

о

с

сГ

+

со

(М

о

ОЗ

см ОЗ

о

ОЗ

о

СО со

ю о &

03 о

о

о ”

о-

©

см

о

о*

со

о "

о “

о

+ + + I

СО

со

о з

о

со

0 3

СО

+ ! +

со

о

о о

оо

1"- со

00 СО

о

F-* со”

»—І

со

+ 1 1 + 1

ігз n т—і —•

N сгз О N о

03 — с о ю •>-*

о о О О (N

со О О 00 о

! 1 + 14-

о

со

00

со

+

о ю

*Tf ю

О ос N ’—1

о о о сч

о о" оо“ о

о

0 3

+ 1 I

о

со

оо

CN

ОЗ со

со

CN

о

сч

со

о

о о о

о '

о*

+ ‘ I 1 + 1 !

со 00 Ю

о

о "

I + I +

ty

Si t: сГ Ьі

яінїїксі

исізиоц

г-, с ч со

lO со ■?>* CO 03 О

CvJ со Tf*

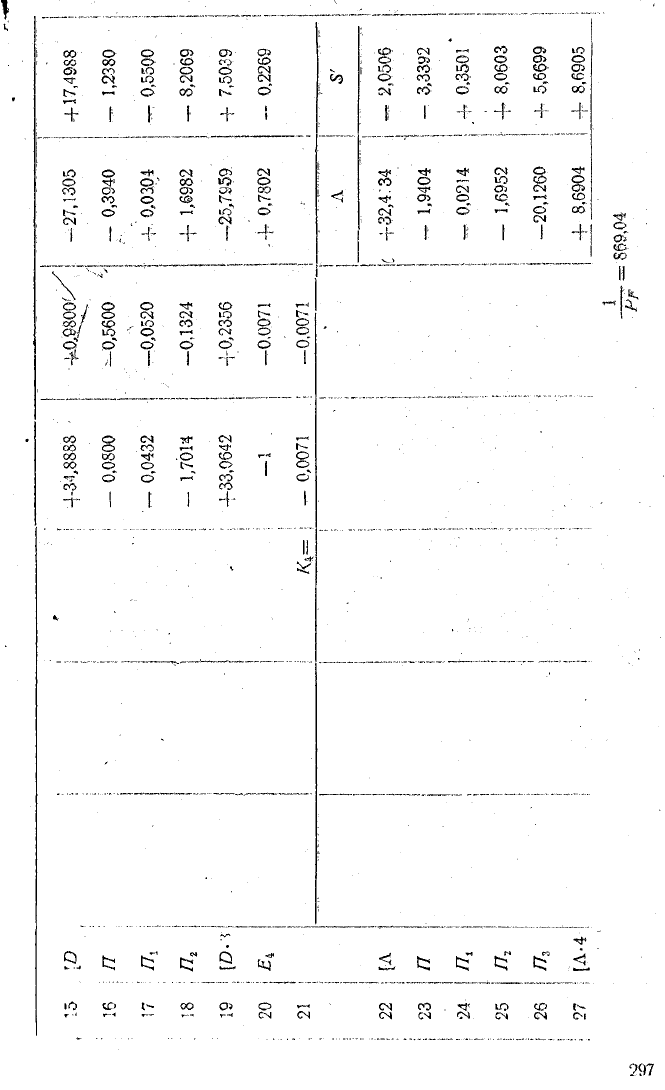
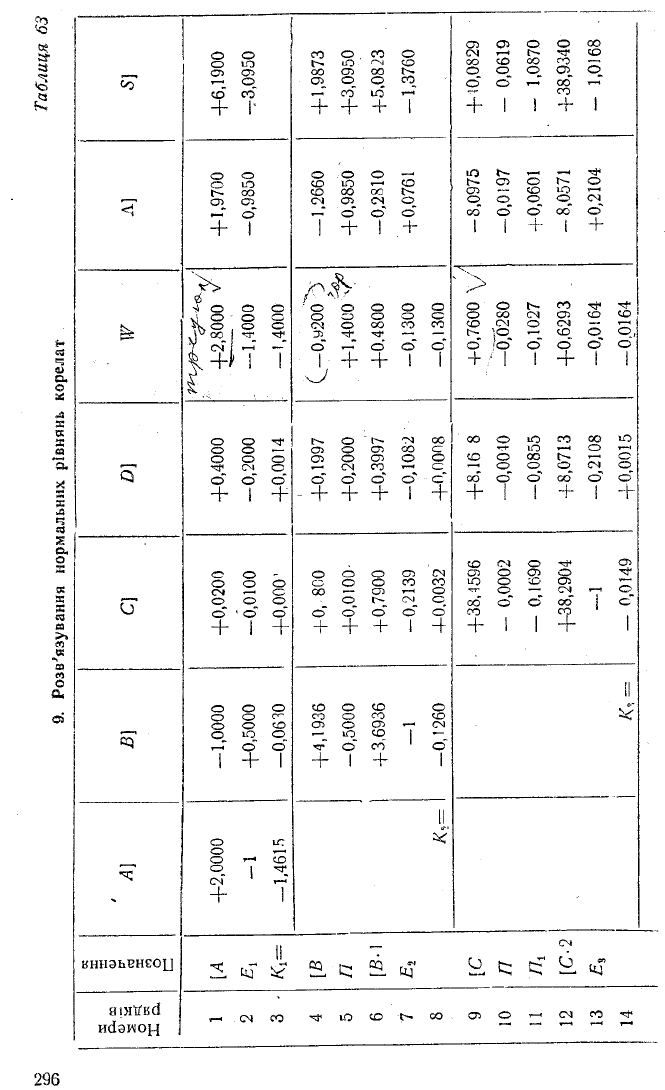
А)

й]

с\

D]

Л]

S'

И

+2

—1 +0,0200

+0,4000

+1,9700

+3,3900

[В

+4,1936 +0,7800

+0,1997

— 1,2660

+2,9073

[С

+38,4596

+8,1608 —8,0975

+39,3229

[D

+34,8888

—27,1305

+ 16,5188

{А

+32,4734

—2,0506

\s

+60,0884

10. Оцінка точності

Середня квадратична помилка одиниці ваги

|і = ± |/ 1 М Ї ? = ± Г >27.

Середня квадратичїіа помилка в логарифмі сторони AF в

одиницях сьомого знака логарифма

triigAF— +І-1 Y = + 37,2.

Відносна помилка в довжині сторони AF

m s

__

mig AF

_

______I

__

s — Л1 -10» “ 1167 4 7 *

де M — модуль переходу від натуральних логарифмів до де

сяткових.

§ 78. ДВОГРУПОВИИ МЕТОД

ВРІВНОВАЖЕННЯ НЕРІВНОТОЧНИХ УМОВНИХ ВИМІРІВ

У тому випадку, коли .виміри є нерівноточними, необхідно

при врівноваженні враховувати їх ваги. Тоді виведені вище

загальні формули врівноваження методом двох груп змінять

ся так.

Нехай маємо систему умовних рівнянь, яку поділимо на

дві групи:

«1 + а2 ^2 + + « л Vn-\-. Wa = О,

t', -}-&2 ~f" •" “Оя 4"®* = 0,

....................................................................... (78,1)

(78,2)

гі + гз ^2 + — + гя vn -И>, .== 0;

®1 ®і 4~ а2 “^2 ~Ь ••• ~Ь °-п V/I -\-Wa =0,

Pi ®1 ~Ь Ра ^2 “Ь ~Ь Ря -f-Byp =0,

І '« t .........................

.............................................

....

.

Ь Vl + х2 4* — + Хя Vn + W% —0.

Припустимо тепер, що нам відоме правило перетворення

коефіцієнтів і вільних членів умовних рівнянь другої групи

Позначимо їх через At, Вь Тit Wu W2, ..., Wi■ Тоді пе

ретворені умовні рівняння можна записати так:

vi-\-A2v2-j-...-}-Anvn-\~ Wy —О,

+ ... -\-BnVn~\- — 0.

(78,3)

7 \ v, + Т, щ + ... + T„ vn + Wt - 0.

* Сумісному розв’язанню умовних рівнянь (78,1) і (78,2)

відповідає така система нормальних рівнянь корелат:

[qaa\ kl-\-[qab]kr\-...-\-[qar\kr

Iqab\k{+[qbb] k2+....+[qbr)kr +

[qar] kx+ [qbr\ Ла+ - + ІЯ™] kr +

I qaA ] [qbA} Л2+ ~ •+ [qrA ] kr+

\qaB]kl-\-\qbB\k2 .+ [qrB\kr +

\qar\kl-\-\iibT\k3+...+ \qrT)kr +

1Яа^ ] /^1+ [ qaB] K2-\-.. -4

+ | qaT\Kt =0,

\ЧЬА]Кг+\чЬВ\КА-~.-\

+ \qbT)Kt +® e = 0 .

...............................(78,4)

[qrA jK ^ rB lK ^ .A

___

-\-\qrT\Kt -j-wr —0,

[дЛЛ] Кi -\-\qAB\ K2+...-\~

+ \qAT\Kt + U ^ ,= 0 ,

[яАВ\Кг+\яВВ\Къ+ ...+

-\-\qBT\K, +

\qAT\Kx-\-{qB 7] К 2+ .. -4

-\-\qTT\Kt -\-Wt =0,

де qi — -j.— величини, обернені вагам вимірів, k і К — коре

лати, що відповідають умовним рівнянням (Першої і другої

перетвореної груп відповідно.

Коефіцієнти і вільні члени умовних рівнянь другої пере

твореної групи, як відомо, обчислюють за такими загальними

формулами:

Аі — а,і -f- at pn -\-bi Pi/- >

B i — [5/ - f -a t P 21 -\-b i р 22- | - ...-| - Л - par,

.................................................................... (78,5)

Т і

— - j - f l j p

t

i ~ f -bi p

1

2 - H • •• - 4 - f /

p t r ,

W j — W j

- f

- W a

p

j

i - j - t w * p у 2 - j -

- \ ~ W r p j r ,

де і — 1,2, 3, ... у n, j = 1, 2, 3

.........

t.

Користуючись неозначеністю множників р, підберемо їх

так, щоб

[qaA[=[qbA\=... = \qrA\=Q,

[qaB] = [qbB}=...= [qrB}= О,

: ...................................................... (78,6)

[qaT] = [qbT\=...^\qrT\ = 0.

При цих умовах нормальні рівняння (78,4) розпадуться

на такі дві незалежні між собою системи:

\qaa]kl-)r \qab}kr\-...-\-[qar\kr-\-wa== 0,

[qab] kx-\- [q bb] ..+ [qbr] кг-\-ііУь= 0,

....................................................................... (78,7)

\qar)kl+\qbr]k2-{-...-\-[qrr\kr-{-Wr = 0;

[qAAWt + lqAB^+.-M qA T\Kt + ^=0,

[qAB\Ki+\4BB\K'l+...+[qBT\Kt+Wr=Q,

[qAT\KM9BT\Kz+...+ [4TT\Kt + W t =0.

(78,8)

Розв’язавши їх, знайдемо корелати k\, k r,K x, К3,

., Kt , первинні і вторинні лопр.авки за формулами

v'i = q-t (di ki-\-bi ..+/•/ kr), (78,9)

if t = qi (At K^+Bi /0,+ ...-{-Ті Kt ) (78,10)

і, нарешті, остаточні поправки

Vi = v'i + Vni .

Для визначення rt допоміжних корелат p після підста

новки у формули (78,6) замість перетворених коефіцієнтів

їх значення (78,5) знайдемо такі системи рівнянь:

[qaa]vn+[qab\va+...+ [qar\vir+[qax\==Q,

[qab] рn+[qbb]Рі 2 + - + [ < 7 М Ріг +[qba]=0,

................................................................................... (78,11)

[qar] Vn+[qbr) p12+ . . . + [qrr]Pir - f [qra] = 0 ;

[qaa] p21+[^fl&] p22+ -+ [< 7«r] Pv + M 1 ==0,

[qab]p,l-\-[qbb]p22-{-...-\-lqbr}p2r-{-[qb$]=0,

................................................................................... (78,12)

[?ar]p21+ [qbr] P22+ ...+ [qrr}?2 ,+ [?гр]=0

і так далі і, нарешті,

\qaa]p и -\{qab)p t2 +...+[?аг]р„+[?ат]=0,

[qab]ptl -\-\qbb]p t2-\--Jr [qbr]ptr +[qbx]=0,

..........................................................................................(78,13)

[qar]ptl - f {qbr)pt2 + -+{q rr] р<, + [ ? г т ] = 0 .

Як бачимо, ці рівняння відрізняються від нормальних рів

нянь корелат лише 'назвою невідомих та вільними членами.

Прослідкуємо тепер, як зміняться виведені вище форму

ли, якщо поділ умовних .рівнянь на дві групи проведемо так:

до першої групи віднесемо ті рівняння, які не мають спіль

них поправок і в яких коефіцієнти при поправках дорівнюють

одиниці. До другої групи будемо відносити ВСІ ІНШІ рііі-

чяння.

Прп цій умові нормальні рівняння корелат, .що'відповіда

ють умовним рівнянням першої групи, «зберуть такого ви

гляду:

»м

[qaa] k^Wa—O,

j qbb] ko-^Wb—Q,

[qrr] kr -\-wr= 0,

або, беручи до уваги, що щ — bt ==.-.. — г,- = 1,

[?]А+™ « = 0,

[q)2k 2-{-wb-=0,

(78,14)

[<7], Аг,0;

тут — суми величин <7 по секціях, які утворюються умов

ними рівняннями першої групи. З рівнянь (78,14) знахо

димо:

Первинні поправки обчислюються за загальною формулою

(78,9). Але, зважаючи на вказане вище правило розподілу

умовних рівнянь на групи, ця формула виглядатиме так:

Підставивши в (78,16) значення корелат (78,15), одер

жимо таку загальну формулу:

де і — 1,2,..., п — номер поправки, s — 1, 2, — номер

секції (умовного рівняння першої групи), в яку входить від

шукувана поправка.

Системи ірівнянь (78,11), (78,12) і (78,ІЗ), з яких визня

чаються допоміжні корелати р, наберуть такого вигляду:

(78,15)

і — qi ks .

(78,16)

(78,17)

Бугай П.Т. Теорія помилок і спосіб найменших квадратів

Подождите немного. Документ загружается.