Бугай П.Т. Теорія помилок і спосіб найменших квадратів

Подождите немного. Документ загружается.

Висота початкової точки А На =192,683 м.

Для визначення висот точок В, С, D, Е -необхідно вимі

ряти лише чотири перевищення. Ми ж маємо їх вісім. Отже,

додаткових перевищень є чотири. Вимір кожного з них обу

мовлює появу ОДНОГО умовного ріВіНЯй'НЯ, суть якого поля

гає в тому, що сума врівноважених перевищень по кожно

му зімкнутому нівелірному полігону повинна дорівнювати

нулю. Позначивши найімовірніші поправки до виміряних зна

чень перевищень ВІДПОВІДНО через V \, V2, . . . , Vs, умовні рів

няння в загальному виді можна записати так:

Л і-И і - Л7—г>7 - h2—v 2 = О,

М - ^ 5 - А8 - ‘Z's + M-'^T = 0>

(72,1)

^З+^З+^б+^б — — ^4 "“ О,

або, підсумовуючи виміряні суми перевищень в напрямах

за рухом стрілки годинника,

v2—v7 —18 мм = 0,

^s+12 мм = 0,

^з+^в+іб мм = 0, (72,2)

v3—'о4+ і'в—14 мм = 0.

За ваги вимірів приймаємо величини, обернено пропор-

ціональні довжинам нівелірних ходів, і обчисляємо їх за

формулою

Рі ~ . (72,3)

Отже, вагу р = 1 матиме нівелірний хід з сі= 10 км.

Для зручності дальших о,бчислень знаходимо величини

<7,-, обернені вагам:

або, беручи до уваги (72,3),

Далі складаємо таблицю коефіцієнтів умовних рівнянь

(табл. 52) і таблицю коефіцієнтів нормальних рівнянь ко

релат (табл. 53).

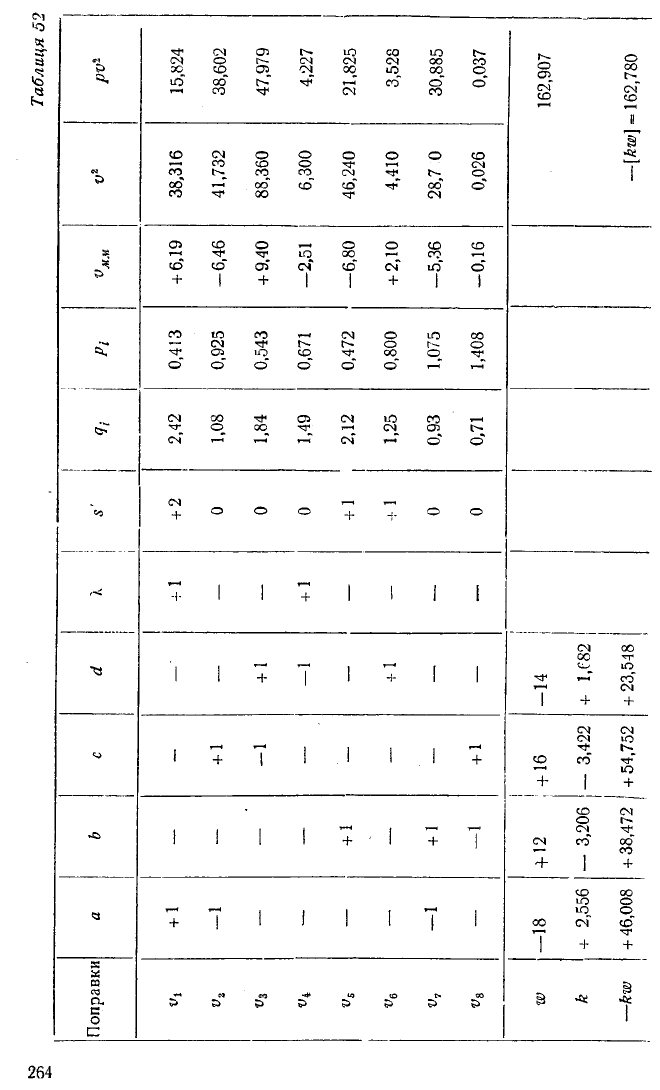
Таблиця 52

X] s')

[qa

+4.43

-0,9 3

—1,08 0 +2,42

-}-4,84

[qb

+3,76

-0,71 0 0 +2,12

[qc

-1-3,63 -1,84 0

[qd

і 4,58 —1,49

+ 1.25

[qk

-•-3,91 + 4,84

\<is'

-i-13,05

Нормальні рівняння корелат будуть:

-1-4,43 А,—0,93 /г2—1,08 As —18 = 0,

-0,93 Лі+3,76 Лг3—0,71 А3 +12 = 0,

-1,08 А,—0,71 А2+3,63 А ,- 1,84 А4+16 = 0, (72,5)

-1,84 А,+4,58 А4—14-0.

Розв’язуючи їх в схемі Гаусса—Дулітля (табл. 54), послі

довно знаходимо корелати:

А, = +2,556,

А, = -3,206,

А3 = -3,422, (72,6)

А4 = +1,682,

найімовірніші поправки до виміряних значень перевищень

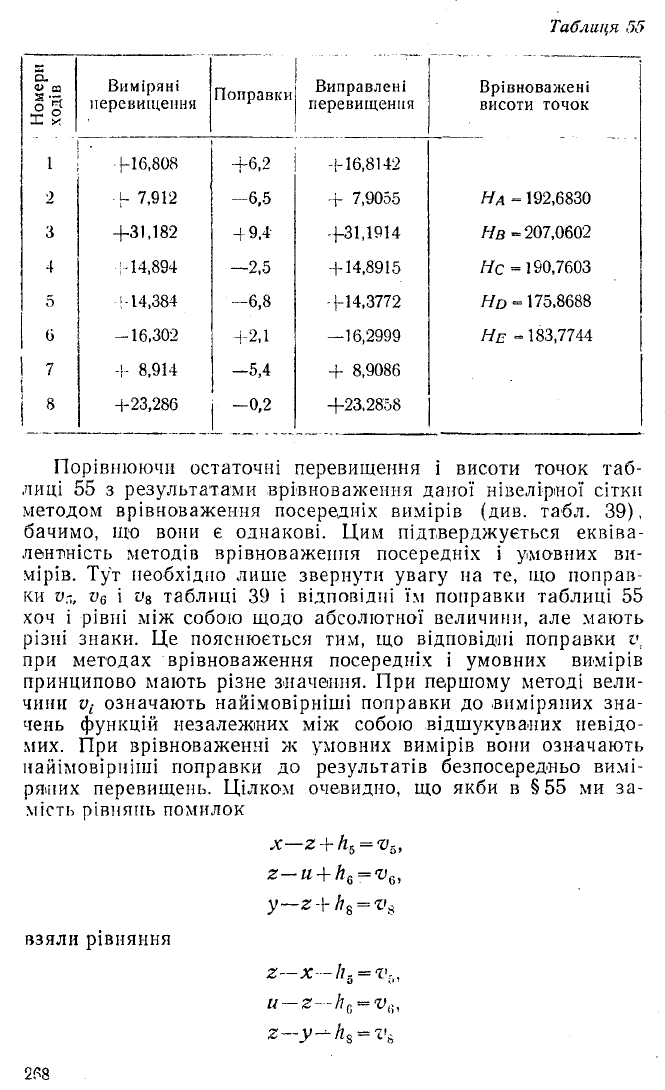
чгі формулами (65,13) і, нарешті, врівноважені перевищення

і висоти точок В, С, D, Е в схемі (табл. 55).

Середню квадратичну помилку [х одиниці ваги обчислюємо

і а формулою (67,1):

162,907 й . г- 0

— ^— = + 6 ,4 м . (72,7)

Середня квадратична помилка, що припадає «а 1 км ні-

иі'лірпого ходу,

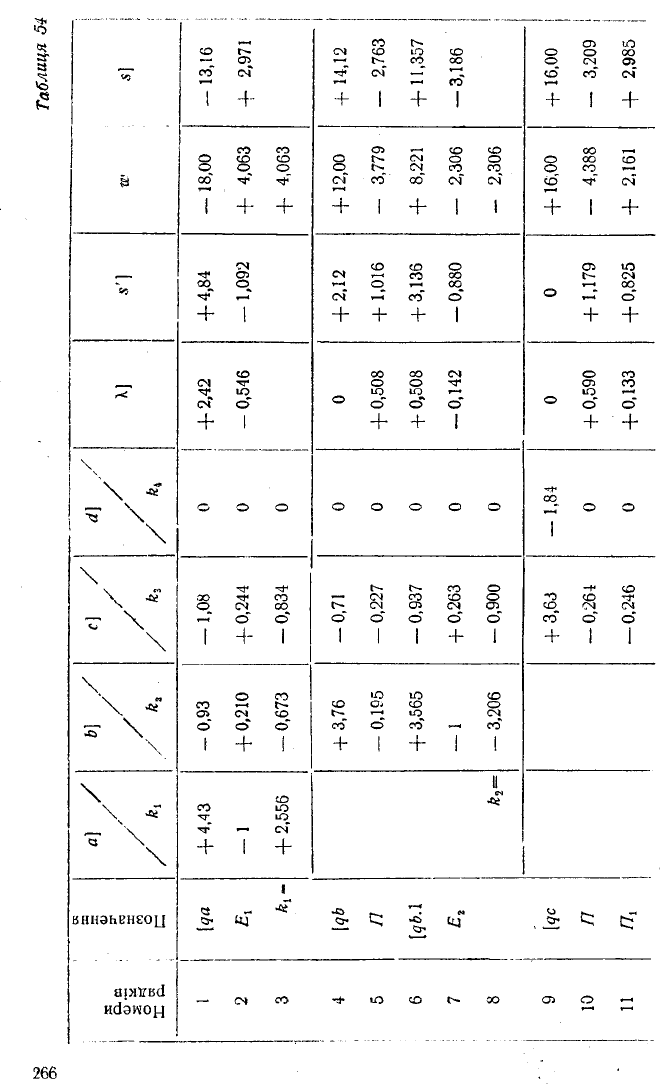
Таблиця 54

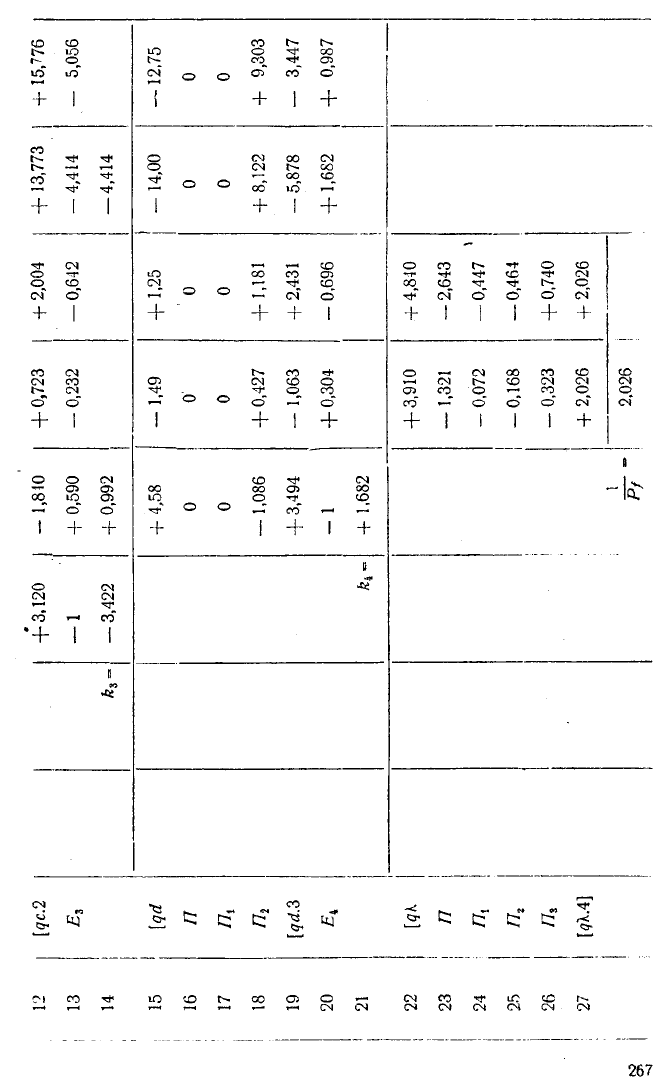
+ 3.120 і -1,810 I +0,723 I + 2,004 I +13,773 j +15,776

СО

r- GO

+ + +

+ I +

»—1

со

«>

•—*

г**

*-*

Tt*

*+>

ОО со со СО

CO о

ол

со

CN CN

со

г—

со

О О

o“

—Г

о со

,-Г

о о

о"

+ I +

со

I +

о CO

^ CN

I-- о

о c n

+ I

I + +

+ I I

&•

C: c? c?

Номери

ходів

Виміряні

перевищення

Поправки

Виправлені

перевищення

Врівноважені

висоти точок

(-16,808 +6,2

4-16,8142

+ 7,912

-6 ,5

4- 7,9055 НА =192,6830

3 +31,182 4 9,4

+31,1914

Н в =207,0602

4 1-14,894

—2,5

4-14,8915

Не =190,7603

!-14,384

-6 ,8

+14,3772 Hd = 175,8688

-16,302

4-2,1

—16,2999 Не =183,7744

-1- 8,914 -5 ,4

+ 8,9086

•

4-23,286 -0 ,2 +23,2858

Порівнюючи остаточні перевищення і висоти точок таб

лиці 55 з результатами врівноваження даної нівелірної сітки

методом врівноваження посередніх вимірів (див. табл. 39),

бачимо, що вони є однакові. Цим підтверджується еквіва

лентність методів врівноваження посередніх і умовних ви

мірів. Тут необхідно лише звернути увагу на те, що поправ

ки vr„ ve і l's таблиці 39 і відповідні їм поправки таблиці 55

хоч і рівні між собою щодо абсолютної величини, але мають

різні знаки. Це пояснюється тим, що відповідай поправки і\

при методах врівноваження посередніх і умовних вимірів

принципово мають різне значення. При першому методі вели

чини vt означають найімовірніші поправки до виміряних зна

чень функцій незалежних між собою відшукуваних невідо

мих. При врівноваженні ж умовних вимірів вони означають

найімовірніші поправки до результатів безпосередньо вимі

ряних перевищень. Цілком очевидно, що якби в §55 ми за

мість рівнянь помилок

x—z + hs = v6,

z —u + he = v 6,

y — z + hs = v s

взяли рівняння

Z — X

и - г —„а

z - y - h a

(а це ми маємо право зробити, тому що при складанні рів

нянь помилок знаки поправок v поки що залишаються не

означеними), то і знаки поправок при обох методах врівнова

ження були б однакові.

Для оцінки точності результатів врівноваження знайдемо

середню квадратичну помилку висоти Я с точки С. Цю ви

соту можна обчислити за формулою

Нс = НА -V ^ 'rv^hi + v,,

або

Нс = На -і А, 1- AIV, (72,9)

де для врівноважених перевищень введено позначення

h і = hl + vl,

hix = hi + vi.

Якщо висоту початкової точки А вважати безпомилко

вою, то точність висоти Я с, очевидно, залежатиме від точно

сті врівноважених перевищень h\ і AjV. Отже, за вагову функ

цію ми можемо взяти функцію (72,9), яку можна записати

у вигляді (68,4):

Нс = Нс°+ >.і^і + М о (72,10)

де

Я с°= НА + А1 + А4; Х, = Х4=1.

Обернену величину ваги функції (72,10) знаходимо при

розв’язуванні нормальних рівнянь корелат за формулою

(68,16). Вона буде дорівнювати:

~ — = [XX.4] =2,026.

' нс

Нарешті, середня квадратична помилка тнс дорівнювати

ме:

тНс = ± ± 9>° мм■

Д В О Г Р У П О В И Й М Е Т О Д

В Р І В Н О В А Ж Е Н Н Я У М О В Н И Х В И М ІР ІВ

§ 7 3 . З А Г А Л Ь Н І З А У В А Ж Е Н Н Я

Основні труднощі при врівноваженні як посередніх, так

і умовних вимірів полягають у розв’язуванні нормальних рів

нянь. При цьому ці труднощі зростають не пропорціонально

зростанню кількості умовних рівнянь або незалежних неві

домих, а в значно більшій мірі. Щоб краще з’ясувати собі

міру зростання цих труднощів, візьмемо систему k нормаль

них рівнянь. Для її розв’язання доведеться спочатку обчис

лити коефіцієнти нормальних рівнянь:

\аа\, [ab], [ас],..., [at], [at], [as],

[bb], [be],..., [bt], [Ы], [bs],

[cc],..., [ct], [cl], [csj,

[tt], [tl], [£s];

кількість їх, враховуючи і контрольні суми [as], [6s], . . . , бу

де:

N~(k + 2) + (k + l) + k + ... + 4 + 3 =

де k — кількість невідомих.

Далі треба обчислити коефіцієнти перетворених нормаль

них рівнянь з покажчиком 1, які позначаються символами:

[bb-1], [ЬсЛ],..., [bt-1], [М-1], [bs-1],

[сс-1],..., [сМ ], [с/• 1 ], [CS-1],

[fM[, [tl-\], [fc-1];

кількість їх

iV, = (&+!) + £+ (£ - ! )+ ...+ 4 -ь З -(*~1)2(* + 4>

Кількість коефіцієнтів перетворених нормальних рівнянь

з покажчиками 2, 3, (к— 1), очевидно, дорівнюватиме

відповідно:

кг {k-2)(k + 3)

2 2

(ft-3)(fe + 2).

З О

Л/ 2'7

А А - 2 =

2 ’

IV 7 > ' 6

- --g- .

Позначивши через Nk' кількість усіх коефіцієнтів нормаль

них і перетворених рівнянь, враховуючи і контрольні суми,

будемо мати:

/V* = 1 • 6 + 2 • 7 + ... + ( k -2 )( k + 3) + ( k - \ ) ( k + 4) + k(k + 5)},

або, проробивши очевидні перетворення:

Nk = 1 { і.(і+ 5 ) + 2-(2 + 5) + ...+ k(k + 5)},

N k = ^ { (12 + 22 + 32+ . . . + £ 2) + 5(1 + 2 + 3 + . . . + £)},

кг 1 jk(k + 1) (2 k-\- 1) ,5k(k + l)\

= Т і

--------

----------

------

-----

/•

Nk = ^ (fe + l) (^ 3 Ll+5),

і, нарешті,

N k - і - k{k + \){k + 8). (73,1)

За цією формулою можна скласти таблицю значень чи

сел Nk при різних k:

(73,2)

кількість нормальних рівнянь k.

До цього необхідно додати, що розв’язування нормальних

рівнянь методом Гаусса не дає можливості всю роботу по,

обчисленню розподілити одночасно між декількома обчис-

k =

Nk 40,

к = 5,

Nk 65,

ю,

= 330,

& = 25,

= 3575,

£ =

50,

- 24650,

k =

100,

= 181800.

що число

зростає

люьачами, тому що обчислення в схемі Гаусса дальших кое

фіцієнтів перетворених нормальних рівнянь знаходиться в

повній залежності від обчислення попередніх.

Все це викликало необхідність розробки таких методів

врівноваження умовних вимірів, при застосуванні яких або

значно зменшується кількість праці по обчисленнях, або є

можливість розподілити її між кількома обчислювачами. Та

кими методами є методи двогрупового, тригрупового та ба-

гатогрупового1 врівноваження умовних вимірів.

Суть двогрупового методу врівноваження полягає в тому,

що всі умовні рівняння, які виникають у даній конкретній

геодезичній сітці, поділяють на дві групи і кожну з них

розв’язують окремо. При цьому при розв’язуванні умовних

рівнянь другої групи їх коефіцієнти і вільні члени спочатку

перетворюють так, щоб в результаті роздільного розв’язуван

ня умовних рівнянь першої групи і перетворених рівнянь дру

гої групи були одержані в сумі такі ж остаточні поправки

до результатів вимірів, як і при сумісному розв’язуванні

всіх умовних рівнянь.

§ 74. ЗАГАЛЬНА ТЕОРІЯ ВРІВНОВАЖЕННЯ

РІВНОТОЧНИХ УМОВНИХ ВИМІРІВ

ДВОГРУПОВИМ МЕТОДОМ

Нехай задано систему т умовних рівнянь, які ми спочатку

поділимо на дві групи. В першу групу віднесемо г, а в дру

гу — t рівнянь, причому r-\-t — т.

alvl + a2v2 + ... -!- anv n + w„ =-=0,

btv 1 + biv.1 + .. . + bnvn +wb =0,

r1 vl + r2v, 4• ... + rnv„ +wr = 0;

'я, V, + a 2 V., + . . . + a„ Vn + W* =0,

P i

V i

+ P 2

V .J + . . . + V n

= 0 ,

г», + x2 v2 + . . . + xn vn = 0,

де v t, Vi, • • • , v n — відшукувані поправки до результатів

вимірів.

Маючи «а увазі згадане в кінці § 73 перетворення коефі

цієнтів і вільних членів умовних рівнянь другої групи, замі

нимо систему умовних рівнянь (74,1) і (74,2) еквівалентною

^ Про ба.гатогруповий метод врівноваження див. И. Ю. П р а н и с -

Праневич. Руководство по уравнительным вычислениям заполняющей

триангуляции II, III и IV классов. Геодезиздат, 1956.

(74,1)

(74,2)