Бугай П.Т. Теорія помилок і спосіб найменших квадратів

Подождите немного. Документ загружается.

Г л а в а V

В Р І В Н О В А Ж Е Н Н Я У М О В Н И Х В И М ІР ІВ

§ 65. ЗАГАЛЬНА ТЕОРІЯ ВРІВНОВАЖЕННЯ

БЕЗПОСЕРЕДНІХ ВИМІРІВ, ЗВ ’ЯЗАНИХ УМОВАМИ

Безпосередніми вимірами називаються такі, коли вимі

рювана величина безпосередньо порівнюється з одиницею мі

ри. Якщо результати, безпосередніх вимірів повинні задоволь

няти будь-які геометричні умови, то такі виміри називають

ся умовними. Так, наприклад, сума кутів я в зімкнутому тео

долітному ході повинна дорівнювати:

S a. = 2d(tl —

або сума перевищень у зімкнутому нівелірному ході повинна

дорівнювати нулю: 2/г ~= 0. Виміри таких кутів і перевищень

і називаються умовними.

Врівноваження результатів безпосередніх вимірів, зв’яза

них умовами, називаються скорочено врівноваженням

умовних вимірів. Загальна теорія такого методу по

лягає ось в чому.

Нехай з результаті вимірів невідомих величин х\, хг,

хп були одержані значення

U, ... , Іп (65,1)

з вагами

Ри Рі, ■■■ , Рп- (65,2)

Припустимо, що ці результати повинні задовольняти г

умов:

Fl(xl, х2, ... , хп) =0,

*2, ••• . Хп)=0, (65,3)

Fr (xlt х2, ... , х„) = 0.

Ці умови, виражені в математичній формі рівняннями

(65,3), називаються умовними рівняннями.

В багатьох випадках умовні рівняння можуть бути склад

ними. З метою спрощення обчислень при врівноваженні до

цільно привести їх до більш простого лінійного виду. Для

цього припустимо, що

хі = + 0 )>

* 2 = /2 + ( 2), (65,4)

х„ = 4 + (я ).

Тут за наближені значення відшукуваних величин х,- взя

то їх виміряні значення а величини (1), (2), ..., (п) — по

правки до них. Через те, що виміри завжди проводяться точ

ними інструментами і, як правило, досить уважно, то резуль

тати вимірів її, 12, In мало відрізняються від істинних

значень відшукуваних невідомих, а тому поправки (1), (2),

. .., (п) будуть малі.

Підставимо тепер в умовні рівняння (65,3) значення неві

домих (65,4):

M V H 1), 12 + (2), ... , /„+(«)} = 0,

/ ^ + (1), /2 + (2), ... , Іп +(«.)> = 0,

/>{/, + (1), /2 + (2), ... , /„+ (/!)}-0 .

Розкладемо ліві частини цих рівнянь у ряди Тейлора, об

межуючись членами з поправками в перших степенях:-

F,(h. 4, .... І.) | " Щ ( П ! - ( g ) , <2)н--. + (а£ -)0С«)-о,

М Л . h , . . '. ) + ( g ) o(l) + ( g ) o (2) + ... + ( | g ) 0W - 0 ,

(65,5)

........

'”> + ( ^ ) / 1) + ( S ) , ( 2> + - + ( s ;) „ W = ° -

Введемо такі скорочені позначення:

Л (Л> ^2» •••» In') —

T72{ii, f>, ..., In)= ,w2,

(65,6)

f"r і l2j •••> In) —

........( £ )

З цими позначеннями умовні рівняння матимуть такий

простий лінійний відносно невідомих поправок вид:

аі 0 ) + «2 (2) + as (3)-f ... + ап(п) + wi - 0,

(1) + b2 (2) + b;i (3) -|-... -f bn (п) + їо2 = 0,

сі (1) + с2 (2) + с3 (3) + '... +с„ (п) -і-да8 = 0, (65,8)

ri ( ! ) + r 2 (2) -І-/*3 (3) + ,.. Н-гп (гс) + ®,. = 0 .

Ці рівняння називаються умов н ими рів н я н н я м и

поправок. Кількість їх дорівнюватиме кількості додат

кових вимірів і додаткових вихідних даних. Отже, завжди

г<7;. При цій умові з г рівнянь (65,8) не можна знайти п

невідомих поправок. Можна було б п—г поправок взяти до

вільними, підставити їх в умовні рівняння і знайти решту

/■ поправок, виразивши їх у функції перших п—г поправок.

Але в такий спосіб можна .визначити безконечну кількість

систем поправок до виміряних значень невідомих. Щоб зро

бити задачу по врівноваженню .вимірів цілком означеною,

вводять додаткову умову, а саме знаходять таку систему по

правок, яка задовольняла б умову

Pi (І)2 +Р-2 (2y - + p s (З)2 + ...+ Р п (я)2 = minimum (65,9)

при нерівноточних .вимірах або

(1 )2 + (2)2 + (3)2 +... -ь (n f - minimum (65,10)

при рівноточних вимірах. Знайдені при и'Йх умовах поправ

ки називаються найімовірнішими.

Таким чином, задача зводиться до визначення умовно

го екстремуму функції (65,9) або (65,10) при умовах (65,8).

У вищій математиці доводиться, що задачу- на умовний

екстремум можна звести до задачі на абсолютний екстремум

нової функції, яка складається так: беруть, наприклад, функ

цію (65,9) і додають до неї умовні рівняння (65,8), помножені

спочатку на так звані неозначені множники Лагранжа: — 2ка,

—2kb, —2kc,..., —2kг . В такий спосіб знаходять функцію

ф “ Рі 0 )2+/>2(2)2+Аі (З)3+ ...+/>„ {nf -

—2cixka (1) —2a2ka (2)—...—2ап ka (м) -2п\ка

—2bxkb [\}—2b2kb [2] — 2b„kb («)—2w2kb— (65,11)

— 2r^kr [1]—2r2kr [2]—...—2r„kr (n)—2wr kr = minimum.

Для визначення мінімуму візьмемо часткові похідні цієї

функції по всіх невідомих поправках і прирівняємо їх до

нуля. З одержаної таким чинам системи рівнянь знайдемо ті

значення поправок (1), (2), (3), (я), які задовольняти

муть умовні рівняння поправок (65,8) і ,при яких сума квад

ратів поправок, помножених на відповідні ваги, буде міні

мальною. Згідно з цим будемо мати:

Ф/ = 2р1(1 )~ 2 а1А0 ~2Ь1кь -2cxkc — ...— 2rxkT =0,

Ф2' = 2/?а(2)—2агка —2b2kb —2 c2kc —... — 2 r2kr = 0,

Ф,' = 2/»,(3)—2а8Лв —263й* - 2 cskc-...- 2 rskr -0 , (65,12)

Ф„ ' = 2p„ {n) — 2an ka — 2bnkb —2cnkc —...—2rnkr =0.

Звідси, після скорочення на 2, легко знаходимо відшуку

вані поправки:

(1) = ~~ (aykn +bikb +ctkc + -rjir),

(2) — — (a2ka -\ b2kb + c2kc + ... + гайг),

(3) = (a:ik„ -Vb^kb -rc^kc + ... ! r ^ r ), (65,13)

(«) = (dn ka H- bn kb + C„ kc + ... +r„ kr ).

• fl

Введені вище неозначені множники ka, kb, kc,...,krв геоде

зичній літературі називаються корелатами. Для їх ви

значення підставимо поправки (65,13), виражені через коре-

лати, в умовні рівняння поправок (65,8). Для першого умов

ного рівняння будемо мати:

а Л

{ 4 “ ( « і

k a

+ b tkb -\-Cxkc -і ... f r xkr ) ) +

Pi }

f ] )

! d2 \ (a2ka b2kb + C2kc + ... f2kr) ( +

•i- an { y - (an ka Л -bn k b + C n kc + ... + rn k r ) j -i- = 0,

або, розкриваючи дужки і підсумовуючи по стовпчиках,

[“ ]*«+[?]*• + [?]*'+-+ [ у К + ^ - 0 . (65,14)

236

Потім підставляємо поправки ,в друге, третє і т. д. умовні

рівняння і, проводячи аналогічні перетворення, одержимо

послідовно:

Ці рівняння разом з (65,14) називаються нормальни

ми рівняннями к о р е л а т. їх, очевидно, буде стіль

ки, скільки є умовіних -рівнянь. Розв’язуючи їх, знаходимо ко-

релати ka, kb, kc,..., kr. Підставляючи їх в рівняння (65,13),

знайдемо значення поправок (1), (2), (3), ..., (п). І, нареш

ті, додаючи ці поправки до виміряних значень результатів

безпосередніх вимірів /і, і2, із. ■■■, hi згідно з формулами

(65,4), одержимо найімовірніші значення невідомих:

х1 = ІіЛ-{\),

х2 = Іг + (2),

*з ~ 4’ ('0))'

ЕЗ тому випадку, коли виміри проведені рівно точно, мож

на припустити, що

рі

2 = ■ • •

— рп — 1-

Тоді рівняння

(65,13), (65,14) і (65,15) наберуть відповідно такого ви

гляду:

(1 )~alka+bf{kb Л С^С +... + l\kr,

(2)*=a2k a + b 2k b + C2k c +r2k r , (65,16)

{п) = an k a + b„ kb 1 C „ k c -i-... -f- rn k r ,

[U(l\ka ~\~\_&b\kb -)-[йС]Лс -4~

[ab]ka -f [bb\kt) -\-[bc]kc -|-

\ac]ku -\-\bc\kb ~Иcc]kc -j-

\ar\ka :-[br\kb -r\cr]kc

..-\-\ar\kr ~0,

,.-\-[br]kf + ® '2 = 0,

.. {-[cr]k, -4-te»s = 0,

-\rr\kr ~j-ffiv = 0 .

(65,17)

§ 66. ЕКВІВАЛЕНТНІСТЬ МЕТОДІВ ВРІВНОВАЖЕННЯ

ПОСЕРЕДНІХ ТА УМОВНИХ ВИМІРІВ

Врівноваження результатів безпосередніх вимірів, які по

винні задовольняти певні умови, можна провести як умов

ним, так і посереднім методами врівноваження. Ці два мето

ди цілком еквівалентні, тобто вони приводять до однакових

результатів. Справді, нехай маємо результати вимірів

невідомих величин Х\, Хг, . . . , х„ , які повинні задовольняти

г умовних рівнянь:

F1(x1, х2, ..., хп ) = 0,

/% (хи х„ хп) = 0,

і . : (бб,і)

Fr fa і, Х2, ••■> -^я) = 01

де п^>г. З цих рівнянь ми можемо визначити г перших неві

домих, виразивши їх у функції решти п—г невідомих. Нехай

в загальному виді ці функції будуть такі:

(■*-/■+її Хг+2, Хц ),

Xo—f.i(xr.f і, Хг + 2і •••> ^п)>

................................................ (60,2)

Xr~-*=-fr(Xr.tr\< ХГ{-2, Хп).

При такій постановці задачі п— г величин хг+і,хг+

,-..,хп

будуть незалежними невідомими, а решта р величин Х\, х2, ■ ■ ■,

х г — функціями перших. При цьому ми можемо скласти такі

системи рівнянь помилок:

/, (*/4-1, 2, Xn ) - L l =*Vl,

f2(xr+1, Xr+h .... xn)-L 2=*v2,

............................................................. (66,3)

fr{X r- 1-і, Xr.f-2, .... Xn ) Lr — Vr \

Xr-1-І Lr+\ Dr4 I ,

Xr-t- 2 — Lr+i — Vr+V, (66,4)

xn -L„ =vn .

Розв’язуючи рів'няння помилок (66,3) і (66,4) при умові

[уу] = minimum або [pvv] — minimum, знайдемо найімовір

ніші значення незалежних невідомих х щ , x,ti, ..., х„. ІІід-

ставляючи їх в рівняння помилок (66,3) і (66,4), одержимо най

імовірніші поправки vt, v2, vr, i>r+i, vr+2, ..., vn до ре

зультатів вимірів Lu L2, Ln• І, нарешті, обчислюємо

значення перших г невідомих за формулами

Отже, ми бачимо, що при врівноваженні чи то посереднім

методом, чи то умовним ми будемо одержувати одну і ту ж

систему поправок до результатів безпосередніх вимірів, яка

задовольнятиме умову (65,9) або (65,10).

Вибір того чи іншого методу врівноваження в кожному

конкретному випадку обумовлюється кількістю тієї праці,

яку потрібно затратити для проведення всіх обчислень по

врівноваженню. В основному вона залежить від кількості

нормальних рівнянь, які доведеться при цьому розв’язувати.

При застосуванні методу врівноваження посередніх вимірів

кількість їх буде дорівнювати кількості

к незалежних неві

домих, а при застосуванні методу врівноваження умовних

вимірів — кількості умовних рівнянь г. Отже, коли к значно

менше г, то врівноваження проводять посереднім методом. Од

нак при остаточному вирішенні цього питання необхідно брати

до уваги ще й ті труднощі, які можуть виникнути при скла

данні рівнянь помилок, оцінці точності тощо.

§67. ВИЗНАЧЕННЯ СЕРЕДНЬОЇ КВАДРАТИЧНОЇ ПОМИЛКИ

ОДИНИЦІ ВАГИ ПРИ ВРІВНОВАЖЕННІ

УМОВНИХ ВИМІРІВ

У попередньому параграфі ми довели еквівалентність ме

тодів врівноваження посередніх та умовних вимірів. Через

те для визначення середньої квадратичної помилки одиниці

ваги при врівноваженні умовних вимірів ми можемо засто

совувати загальну формулу

де k — кількість незалежних невідомих. При наявності г

умовних рівнянь

(66,5)

хг =Lr -\-vr -

(/jffS l, (67,1)

тобто середня квадратична помилка одиниці ваги при врів

новаженні умовних вимірів дорівнює квадратному кореню із

суми добутків квадратів поправок на ваги, поділеної на кіль

кість умовних рівнянь. Очевидно, що при врівноваженні рів

поточних умовних вимірів середня квадратична помилка од

ного виміру буде дорівнювати:

(67/2)

Величину [pvv] у випадку нерівноточних вимірів можна

визначити двома способами.

1. Знайдені поправки і>ь V2, ■ ■■, vn підносять до квад

ратів, множать їх на відповідні ваги і результати підсу

мовують.1

2. Візьмемо рівняння (65,13), які запишемо в такому

вигляді:

PlV, - (lyku -ь bxkb + ... -f r{kr ,

p2v2*=a2ka

b2kt +

r 2kr

Pn ‘Vn ^ ka -f- bn kb }-... 4' ^ и kr .

Помножимо праві і ліві частини цих рівнянь на V\, v2,

. . . , vn відповідно і підсумуємо добутки по стовпчиках:

[pvv] = [агі] ka + [bv] kb +... -і- [rv] kr. (67,3)

Але з умовних рівнянь (65,8) видно, що

[av] =.—ж1,, [bv]=—w2, ..., [гс>] = — wf . (67,4)

Підставивши ці значення в (67,3), одержимо:

\pvv] = —{w^a + w2kb +... +ZVr kr ),

або

[pvv] = —■ [wk]. (67,5)

і Надалі, для зручності написання формул, ми будемо поряд з по

значеннями для поправок (1), (2), (я) іноді вживати також позна

чення vvvv ... ,Vn ,

При врівноваженні рівноточних вимірів ця формула на

бере, очевидно, такого вигляду:

[о т] = — \w k}. (67,6)

Формули (67,5) і (67,6) є контрольними при обчисленні

цих сум першим способом.

§ 68. ВИЗНАЧЕННЯ СЕРЕДНЬОЇ КВАДРАТИЧНОЇ ПОМИЛКИ

І ВАГИ ФУНКЦІЇ ВРІВНОВАЖЕНИХ ВЕЛИЧИН

Нехай маємо функцію

/ (I, II, III, ... , N) (68,1)

врівноважених величин 1 = l-f-(l), II = 2+(2), III — 3+(3),

. . ., де цифрами 1, 2,3, ... позначені виміряні значення від

шукуваних величин, а (1), (2), (3), ... — поправки до них.

Запишемо функцію (68,1) в такому вигляді:

/{1+(1), 2 + (2), 3 + (3),(68,2)

Через те, що поправки (1), (2), (3 ),

......

— величини малі,

ми можемо функцію (68,2) розвинути в ряд Тейлора, об

межуючись при цьому членами з поправками в перших сте

пенях:

/{1 + (1), 2 + (2), 3+ (3), ...}=/(1, 2, 3,...)+ .

Позначивши часткові похідні

df , df *. Of , /г-о

й = Ж 2’ (68,о)

одержимо вираз для функції (68,2) в такому лінійному .виді:

/{1 + (1), 2 + (2), 3 + (3), ...}=/(1, 2,3,...) +

+ Х3(1) + Х2(2) -г ?-3(3) + ... + Хя (л.). (68,4)

Для визначення оберненої величини ваги цієї функції ми

не можемо при врівноваженні рівноточних умовних вимірів

застосовувати відому нам з теорії помилок загальну фор

мулу

- т %

гому що вона справедлива лише для функцій незалежних

аргументів х, у, z, .... Поправки ж, що входять у функцію

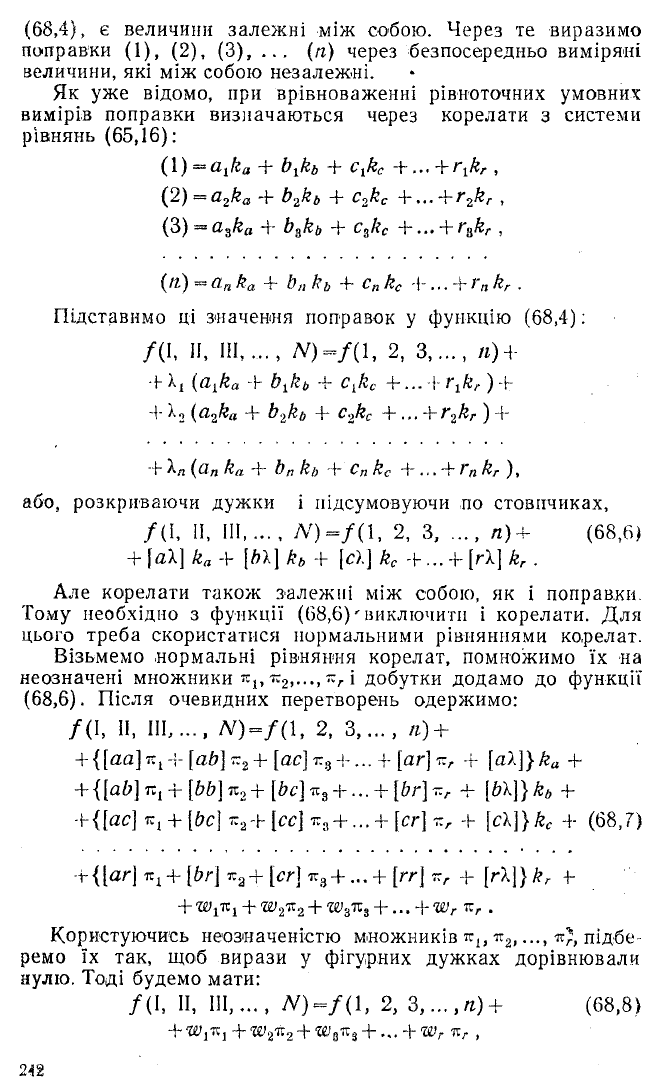
(68,4), є величини залежні між собою. Через те виразимо

поправки (1), (2), (3), ... (п) через безпосередньо виміряні

величини, які між собою незалежіні.

Як уже відомо, при врівноваженні рівноточних умовних

вимірів поправки визначаються через корелати з системи

рівнянь (65,16):

(1) = ^ ^ + Ь^ь + cxkc +...+r1kr ,

(2) = o,2ka + Ьукь 4" c2kc 4"••• Л'ї'чЬ'г ,

(3) = d3ka + b$kb + cskc +... + гзkr ,

(ft) ^ -f" Ьц к tj -f- Cn kc l'n for '

Підставимо ці значения поправок у функцію (68,4):

/(I, II, III,..., N) —f(l, 2, 3,..., n) +

•f X, (aLka + bxkb + ctkc +... -I- rxA,) +

-\- X2 (CLyka + b 2kb + C2kc + ... + f 2kr ) "4"

+ К {an k„ + bn kb + cnkc + ... + r„kr),

або, розкриваючи дужки і підсумовуючи по стовпчиках,

/(І, И, III

.......

А 0=/(1, 2, 3, ..., я)+ (68,6 )

+ [аХ] ka + [ftX] kb + [с).] kc -ь ... + [rX] kr.

Але корелати також залежні між собою, як і поправки

Тому необхідно з функції (68,6)' виключити і корелати. Для

цього треба скористатися нормальними рівняннями ко,релат.

Візьмемо .нормальні рівняння корелат, помножимо їх на

неозначені множники Kj, і добутки додамо до функції

(68,6). Після очевидних перетворень одержимо:

/(I, II, III,..., N)=f(1, 2, 3,..., п) +

+ {[аа}т.1 -\-[аЬ]~г+{ас}т.9-\... + [аг]т.г + [a\]}ka +

+ {[аЬ]гч + [ЬЬ]к2+[Ьс]ъ3 + ... + [Ьг]~, + +

+ {[ac] ir, + [be] r 2+ [cc] ir3 + ... + [cr\ ~r + [cX]}£c + (68,7)

-f{[a r] rcx+[&r] *а+ [с г] rc8 + ... + [rr] t:, + [rX]}£ r +-

+ W1Kl + W2'X2 + W.i Щ + ...+Wr IT, .

Користуючись неозначеністю М'НОЖНИКІВ тс1, 1Г2) ..., itj, підбе 

ремо їх так, щоб вирази у фігурних дужках дорівнювали

нулю. Тоді будемо мати:

/(I, II, III,..., N) = / (1, 2, 3,..., п) + (68,8)

+ WjTCj + W%k2 + Weu3 + . + Wr ъг ,